重視函數應用賞析經典考題
■錢偉密 張啟兆
函數是描述現實世界變化規律的數學模型,也是分析和解決實際問題的重要工具,函數的應用主要體現在兩個基本方面:一是運用函數的思想方法思考、解決其他數學問題,二是運用函數的思想方法描述、分析、解決實際問題。因此,我們要重視函數應用,提升核心素養。
題型1:函數零點所在區間的判斷
確定函數f(x)的零點所在區間的常用方法:(1)定義法,已知函數y=f(x)在區間[a,b]上的圖像是一條連續不斷的曲線,當f(a)·f(b)<0時,函數f(x)在區間(a,b)內至少有一個零點;(2)圖像法,一個函數由兩個初等函數構成,如函數f(x)=g(x)-h(x),可作出y=g(x)和y=h(x)的圖像,其圖像交點的橫坐標即為函數的零點。
例1 函數f(x)=2x-1+x-5 的零點所在的區間是( )。
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
解:因為函數y=2x-1與y=x-5 在R上都是增函數,所以f(x)=2x-1+x-5在R上單調遞增,故函數f(x)=2x-1+x-5最多有一個零點。由f(2)=22-1+2-5=-1<0,f(3)=23-1+3-5=2>0,根據函數零點存在性定理知f(x)=2x-1+x-5有一個零點,且該零點所在區間(2,3)內。應選C。
評注:要理解函數零點與方程的根的關系:方程f(x)=0有實數解?函數y=f(x)有零點?函數y=f(x)的圖像與x軸有公共點。
題型2:函數零點中的新定義問題


解:當x∈[0,1)時,[x]=0,f(x)=x;當x∈[1,2)時,[x]=1,f(x)=x-1;當x∈[2,3)時,[x]=2,f(x)=x-2;當x∈[3,4)時,[x]=3,f(x)=x-3;當x∈[4,5)時,[x]=4,f(x)=x-4,…。
作出兩個函數f(x)=x-[x](x≥0)和y=kx的圖像,如圖1所示。

評注:本題考查分類討論,數形結合以及轉化思想的應用。
題型3:應用所給函數模型解決實際問題
應用函數模型解決實際問題的幾個注意點:(1)認清所給函數模型,弄清哪些量為待定系數;(2)根據已知條件,確定模型中的待定系數;(3)利用該模型求解實際問題。


(1)首次服藥后,藥物有療效的時間是多長?
(2)首次服藥1h后,可否立即再次服用同種規格的這種藥物?
參考數據:lg2≈0.3,lg3≈0.477。
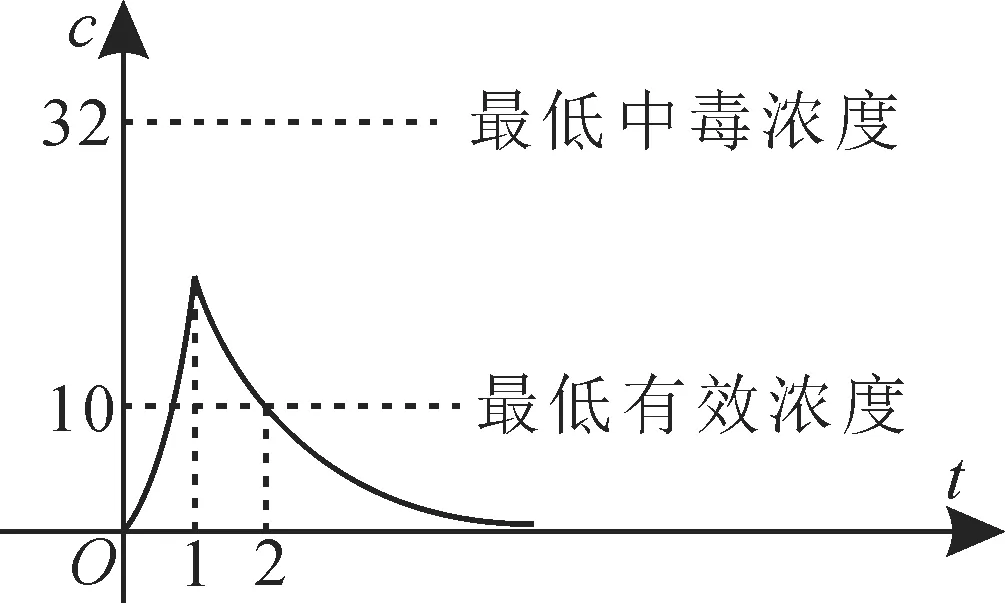
圖2

評注:解答函數模型應用問題的關鍵是審題,對于給出圖形的問題,要文圖對照,即在閱讀文字、符號的同時,一定要閱讀圖形,因為圖形也是數學語言。
題型4:構建函數模型解決實際問題
構建二次函數模型,常用配方法、數形結合法以及分類討論的思想求解;構建分段函數模型,應用分段函數分段求解的方法;構建指數函數、對數函數、冪函數模型的關鍵是理解和掌握這三種函數的圖像與性質。
例4 我國每年浪費的糧食總量至少能養活2 億人,而全球有近6.9 億人處于饑餓狀態。習近平總書記對制止餐飲浪費作出重要指示,強調要“堅決制止餐飲浪費行為,切實培養節約習慣,在全社會營造浪費可恥,節約為榮的氛圍”。在各級政府的大力倡導下,人們的節約意識逐步提高,浪費的糧食以每年20%遞減,從2021年開始計算,我國最早從哪一年開始能使浪費的糧食不超過2021年浪費糧食總量的5%? ( )。(參考數據:lg2≈0.301)
A.2032 B.2033
C.2034 D.2035

因為n∈N*,故n≥2035。應選D。
評注:求解函數應用問題的一般程序:審題—建模—求模—還原—反思回顧。


