基于聯邦濾波的異質異步多傳感器組合導航算法*
姚曉涵 陳 帥 楊 博 李 杰 張 敏
1.南京理工大學自動化學院,南京210094 2.中國船舶工業綜合技術經濟研究院,北京100081
0 引言
為了提高導航系統定位精度和容錯性能,發展多傳感器組合導航是目前最常采用的有效策略。在現有的多傳感器信息融合研究中,大多假定各個導航傳感器同步地將數據傳遞給融合中心[1]。然而,在實際系統中,由于信號變化速率相差較大、檢測裝置采樣周期不同等原因使各個傳感器的采樣速率不盡相同,且由于傳感器固有延遲和通信延遲的不同,使融合中心接收到的數據也不同步。此外,融合導航濾波過程中會遇到各種各樣的干擾,若動力學模型信息受到擾動,或多傳感器觀測信息含有異常誤差,那么最終的導航濾波解必定會和真實值有較大誤差。因此,為了提高組合導航系統定位精度,研究異質異步多傳感器信息融合算法具有重要意義。
方崢等提出了基于子濾波器方差陣修正的多源信息非等間隔聯邦濾波算法,解決無重置聯邦濾波器在應用于多源信息非等間隔濾波時的適應性問題[2]。該算法有效改進了濾波器的估計性能。文獻[3]針對多傳感器非等間隔數據采樣問題,采用時間與量測更新分離的異步非等間隔聯邦濾波算法進行信息融合,并對濾波器結構進行改進以減少算法復雜度。Narjes D等提出了一種基于變分貝葉斯逼近的多傳感器自適應卡爾曼濾波算法[4]。該濾波算法自適應地估計傳感器的測量噪聲方差,對傳感器的異常測量具有較強的魯棒性。文獻[5] 在常規KF基礎上加入了基于新息的方差匹配自適應濾波技術,有效減小了異常情況下的導航誤差。
本文針對組合導航系統中多個傳感器采樣頻率不同且融合導航濾波過程中動力學模型信息受到擾動的問題,提出一種基于聯邦Kalman濾波的多尺度自適應組合導航信息融合算法。該算法把各傳感器的數據按照最低尺度進行分塊處理,通過狀態和觀測的擴維,得到多尺度系統模型,并引入了自適應因子以控制量測預測值。通過仿真,驗證了本文所提信息融合算法可有效提高異步異質多傳感器組合導航系統的定位精度。
1 多傳感器組合導航系統建模
1.1 多尺度模型描述
設有N個導航傳感器i(i=1,2,……,N)以不同采樣率Si進行觀測,且彼此間的采樣是異步的,采樣率間的關系滿足:
Sj+1=njSj1≤j≤N-1
(1)
式中nj為已知正整數。
i(i=1,2,…,N)既表示傳感器,也表示尺度。具有最低采樣率SN的第i=1個傳感器對應于最粗尺度,具有最高采樣率SN的第i=N個對應于最細尺度,傳感器i=1,2,…,N-1的采樣率介于兩者之間,依次升高[6]。
在最高采樣率下多傳感器組合導航系統狀態方程和觀測方程一般可描述為:
X(N,K+1)=F(N,k)X(N,k)+W(N,k)
(2)
Z(i,k)=H(i,k)X(i,k)+V(i,k)
(3)
式中,X(N,k)∈Rn×1是最高尺度N上k時刻的狀態量,F(N,k)為系統一步轉移矩陣,系統噪聲W(N,k)∈Rn×1是均值為零的高斯白噪聲,Q(N)為其協方差,Z(i,k)∈Rqi×1(qi≤n)為第i個傳感器在采樣率Si下獲得的第k個觀測值,H(i,k)∈Rqi×n為觀測矩陣,觀測噪聲V(i,k)∈Rqi×1均值為0的高斯白噪聲,其協方差為R(i),且不同采樣率下的觀測噪聲互不相關[7]。初始狀態向量X(N,0)為一隨機變量,且假設X(N,0),W(N,k),V(i,k)彼此間獨立[8]。
在濾波前先確定融合的周期,根據這個周期,把各傳感器的數據按照最低尺度進行分塊處理。對于每一塊內的數據,計算各采樣率高于這個融合周期的傳感器在這個融合尺度上的平滑信息。
1.2 基于聯邦卡爾曼濾波的組合導航模型
本文中聯邦卡爾曼濾波以慣性導航系統為基礎,其它系統分別與SINS構建子濾波器。選取東北天地理坐標系作為導航坐標系。狀態量選用SINS慣性器件的誤差量,并加入陀螺的常值誤差、隨機誤差以及加速度計的隨機誤差,得到18 維的狀態矢量X:
X=[φEφNφUδVEδVNδVUδLδλδH
(4)

1)GNSS/SINS子濾波器
根據式(2),GNSS/SINS子濾波器的狀態方程可表示為:
(5)
GNSS/SINS子濾波器的量測方程為:
ZGNSS(t)=HGNSS(t)XGNSS(t)+VGNSS(t)
(6)
2)ALTM/SINS子濾波器
ALTM/SINS的組合模型也以18維的SINS誤差量作為狀態量,根據式(2),其子濾波器的狀態方程可表示為:
(7)
ALTM/SINS子濾波器的量測方程為:
ZALTM(t)=HALTM(t)XALTM(t)+VALTM(t)
(8)
3)AHRS/SINS子濾波器
AHRS/ SINS的組合模型也以18 維的SINS 誤差量作為狀態量,根據式(2),其子濾波器的狀態方程可表示為:
(9)
AHRS/ SINS子濾波器的量測方程為:
ZAHRS(t)=HAHRS(t)XAHRS(t)+VAHRS(t)
(10)
2 異質傳感器信息融合
2.1 自適應狀態估計求解
卡爾曼濾波是一種線性最小方差估計,可以實時估計系統的誤差參數,主要通過遞推計算,用先驗值和最新觀測數據中得到的新值的加權平均來更新狀態估計[9]。離散化后的系統模型具體為:
(11)
自適應濾波在濾波計算過程中可以抑制濾波器的發散。它通過觀測數據實時得到預測修正值,對未知的或者不確定的系統模型和噪聲參數進行估計和修正。下面推導一種基于新息的自適應卡爾曼濾波算法,通過對新息方差的極大似然估計,解決外部量測噪聲強度不確定時系統的濾波穩定問題。具體如下:
狀態一步預測:
(12)
一步預測誤差協方差:
(13)
濾波增益:
(14)
狀態估計:
(15)
估計誤差協方差:
Pk=(I-KkHk)Pk,k-1
(16)
濾波器的新息序列rk狀態和其新息方差Crk的表達式為:
(17)
(18)
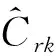
(19)
則量測信息的協方差陣為:
(20)
為了控制狀態模型異常和觀測信息異常對系統狀態參數估計的影響,利用抗差估計原理構造如下極值函數:
(21)
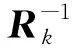
(22)
對式(21)求極值后則有:
(23)
將信息向量方程和狀態預測信息的誤差方程帶入式(23),可得狀態參數的抗差自適應濾波解為:
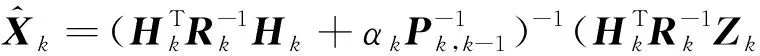
(24)
2.2 信息分配因子構造
從式(23)的抗差自適應解的表達式中可以看出,利用抗差估計對觀測信息進行檢測,如果觀測信息有異常,則相應的等價權矩陣就會減小,從而可以控制觀測信息異常的影響。并且利用自適應濾波方法根據觀測信息對動力學模型進行檢測,如果相應的動力學模型有異常,則相應的自適應因子αk就減小,從而可以控制狀態模型預測信息異常的影響[10-11]。如果系統的動力學模型和觀測信息均正常時,整個系統就可以正常利用動力學模型和觀測信息進行最優估計,此時的抗差自適應濾波就是標準的Kalman濾波[12]。
由于預測殘差信息可以較好地反應擾動影響,因此可以采用預測殘差構造自適應因子αk,采用三段函數法可以表示如下:
(25)
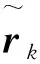
(26)
3 仿真校驗
為了驗證本文所提多尺度自適應組合導航信息融合算法的有效性,將所提方法用于SINS/GNSS/ALTM/AHRS組合導航系統,利用Matlab進行相應的仿真試驗。仿真中各傳感器誤差參數設置如表1所示。

表1 傳感器誤差參數設置
仿真時間為10min,圖1給出了仿真中載體的飛行軌跡。飛行過程中包括左拐彎、右拐彎、上升、下降、加速、減速、平飛等任務。
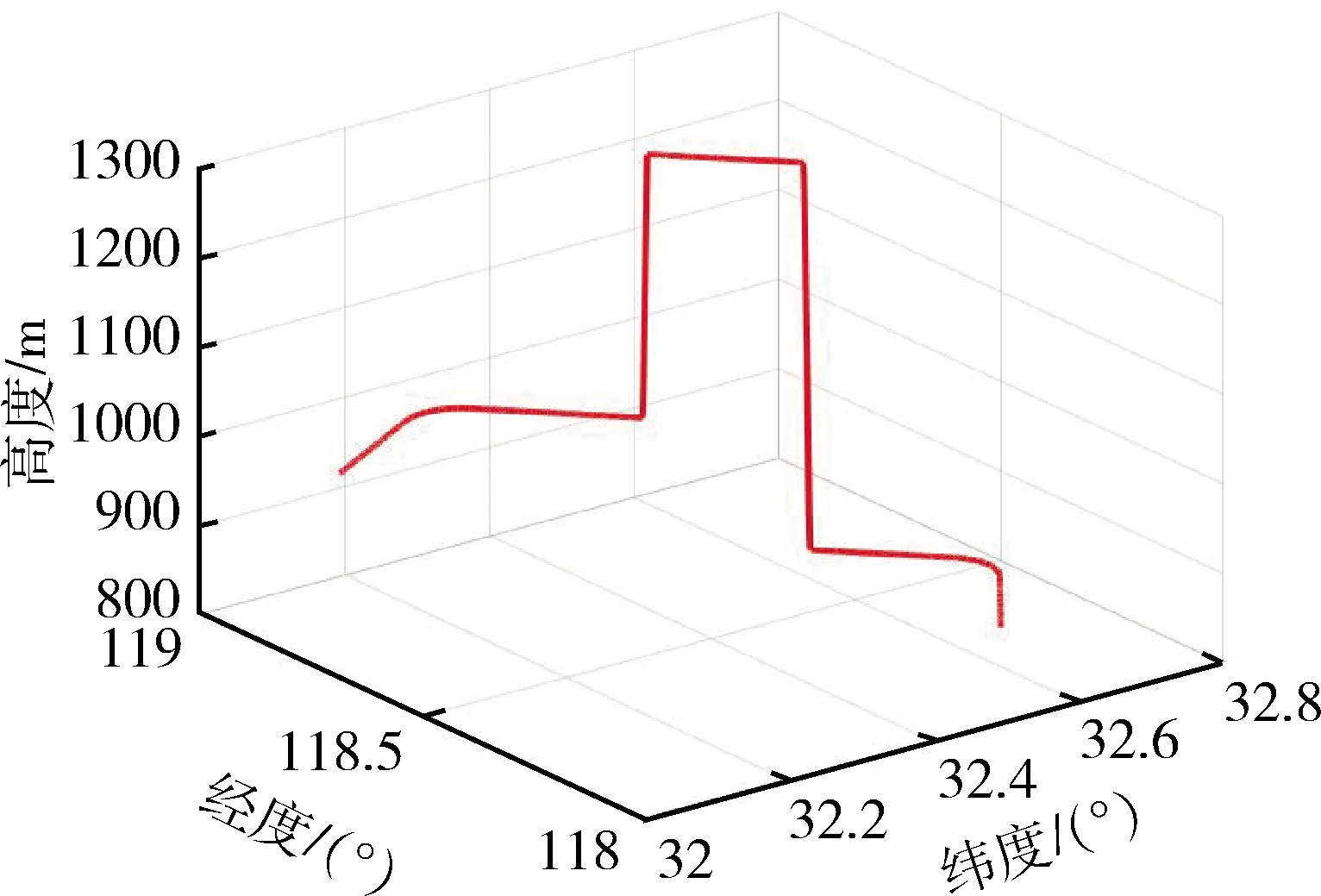
圖1 飛行軌跡
設置SINS解算更新周期為0.02s,AHRS量測更新周期為 0.1s,GNSS量測更新周期為1s,ALTM量測更新周期為1s,模擬傳感器多采樣率情況。主濾波器將局部濾波器的輸出信息進行最優融合,更新周期為1s。假設具有最高采樣率的SINS采樣均勻,為模擬傳感器量測延遲情況,對GNSS、ALTM、AHRS的量測信息加入隨機延時。為模擬傳感器量測異常和動力學模型擾動情況,在100~200s不使用AHRS的量測信息,在400~500s不使用ALTM的信息。
對于相同的SINS、GNSS、ALTM、AHRS仿真數據,分別采用本文算法與文獻[5]中所提抗差算法(后面簡稱算法1)進行信息融合,然后比較兩者的均方根誤差。仿真中,本文所提算法將數據進行分塊,且每個數據塊均包含有4種導航傳感器的量測信息,以數據塊為單位進行濾波。仿真結果如圖2~3所示。算法1將與 GNSS、ALTM、AHRS量測對應的SINS解算結果存儲,當延遲的量測信息到達時,將其與存儲的SINS解算結果之差作為觀測量進行濾波,得到狀態估計,并將此狀態估計通過時間更新,遞推得到當前時刻的狀態估計。仿真結果如圖4~5所示。表2給出了2種融合算法導航結果的數據統計值。
綜合分析圖2~5和表2可得,本文算法與算法1融合結果相比,位置與速度精度均有提高。其中,天向速度和高度的誤差減小幅度分別達18%和23%,在異質多傳感器異步采樣的情形下,能有效提高濾波器的估計精度,從而有利于提高導航系統的定位精度。
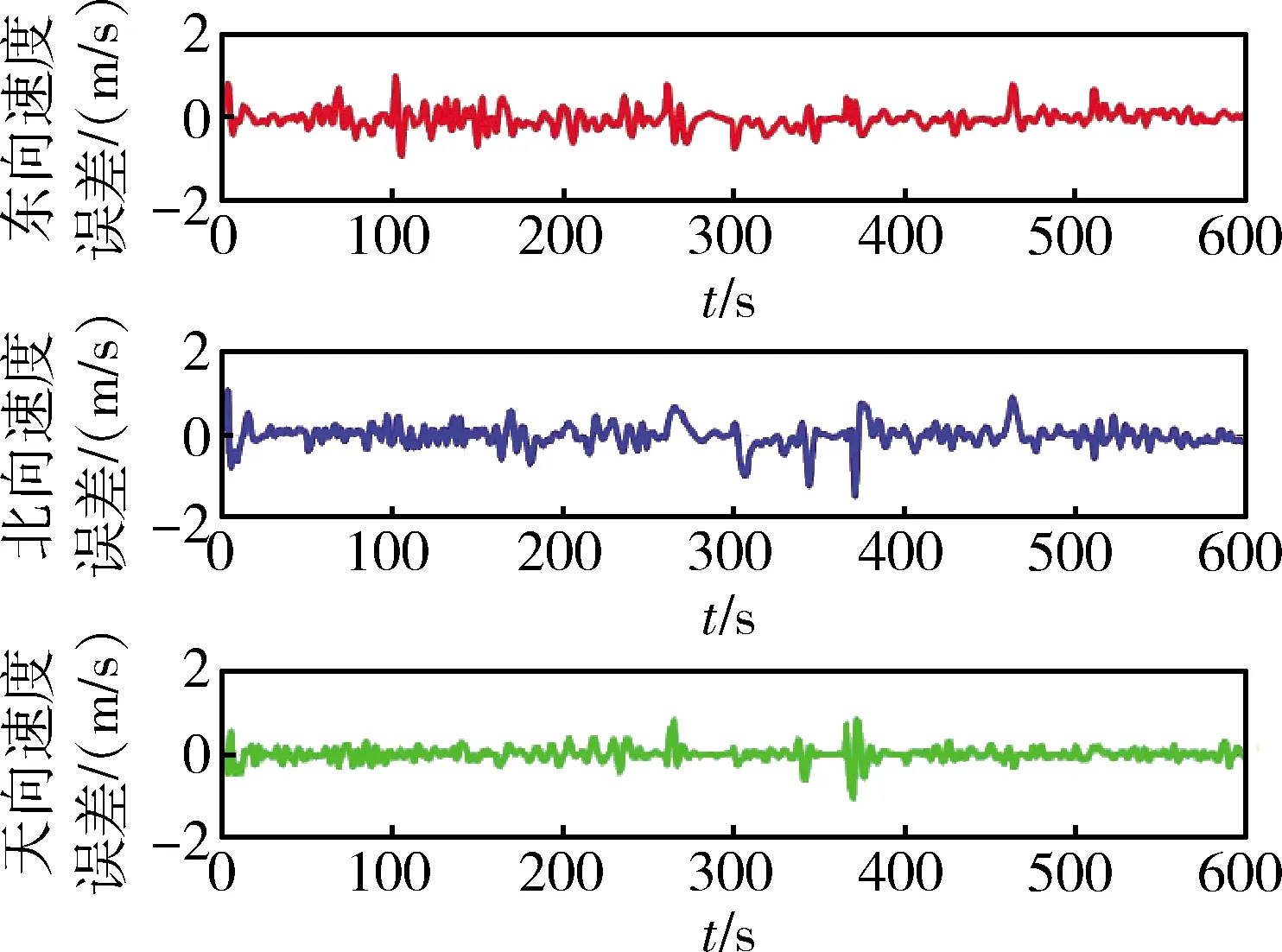
圖2 本文算法速度誤差
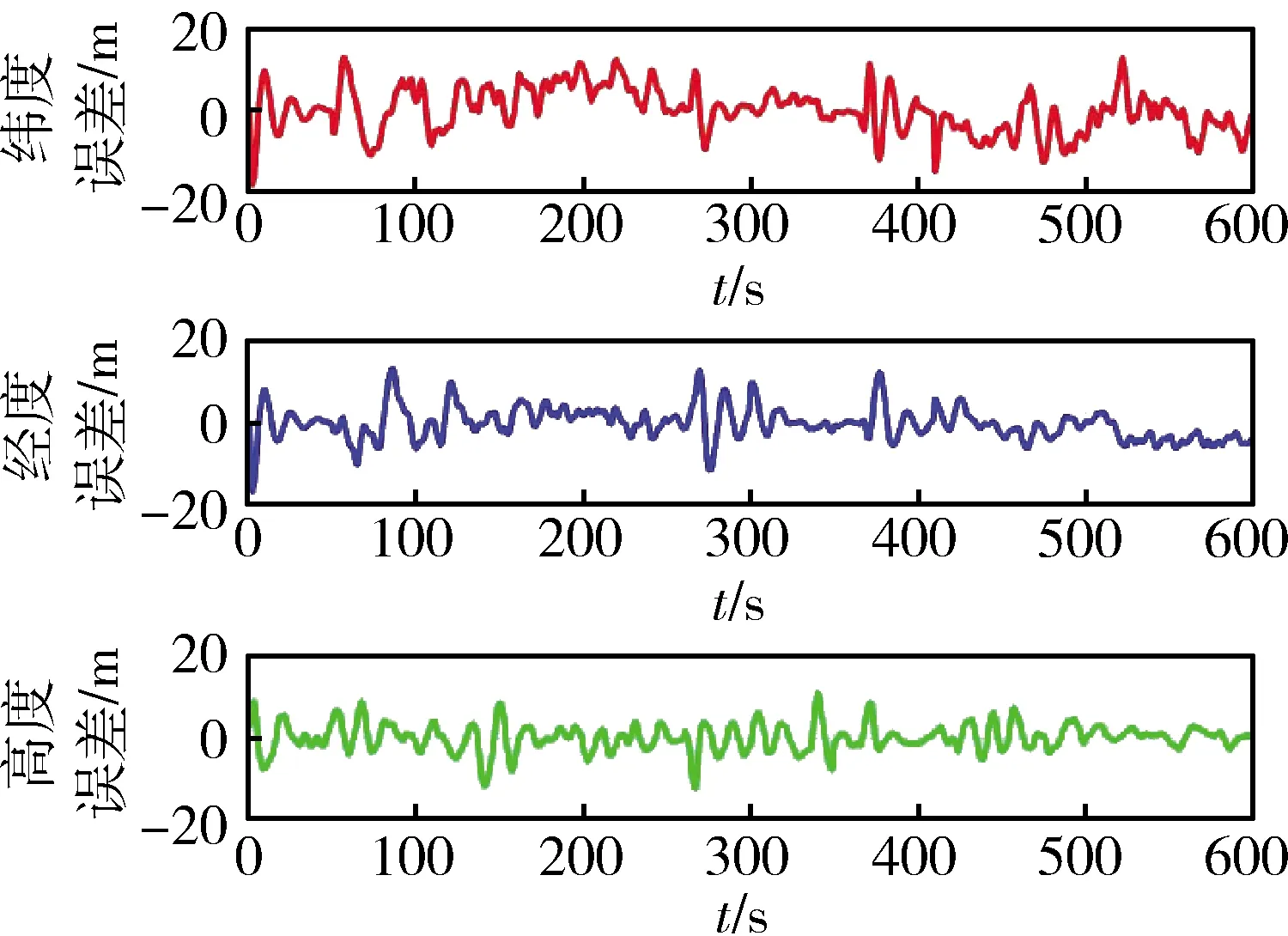
圖3 本文算法位置誤差
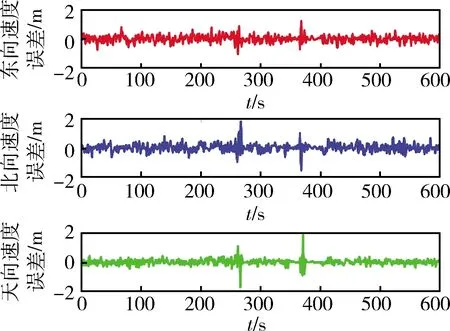
圖4 算法1速度誤差
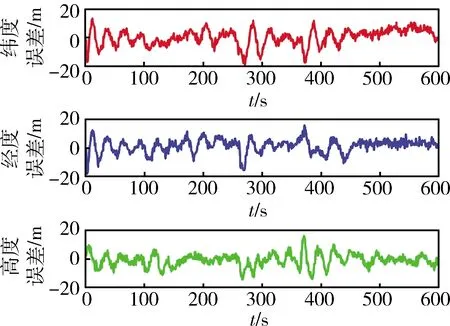
圖5 算法1位置誤差
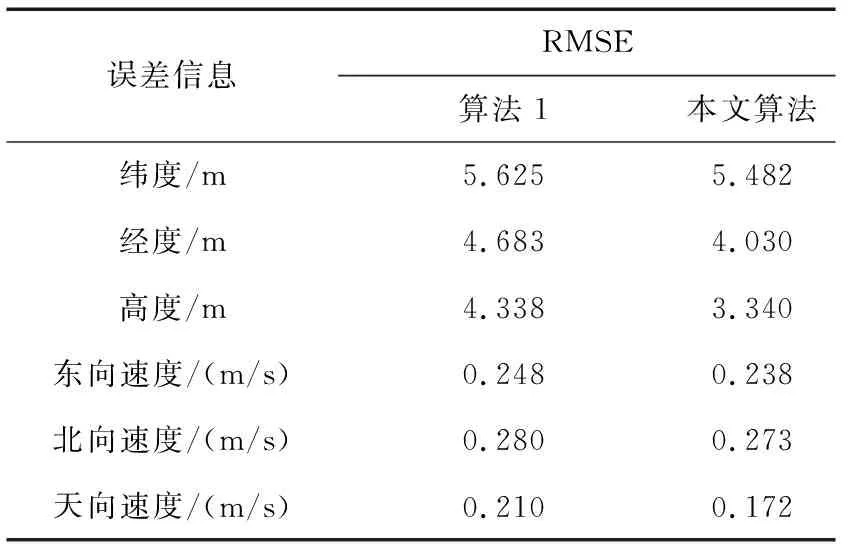
表2 均方根誤差結果對比
4 結論
本文詳細介紹了多尺度系統模型和自適應信息融合設計方法,以飛行器上SINS/GNSS/ALTM/AHRS多源組合導航系統作為研究對象,通過MATLAB仿真,將本文所提算法融合效果與前人研究的抗差濾波算法進行對比。實驗結果表明,經異質異步多傳感器組合導航算法進行數據融合后,位置精度和速度精度均有一定的提高。在計算復雜度允許的情況下,本文算法能解決一定范圍內的量測延遲,并且能處理試驗中比較常見的量測異常和動力學模型擾動的問題。

