彈載慣測組合加速度計振動響應影響因素研究

邱 東

湖北航天技術研究院總體設計所， 武漢 430040

0 引 言

慣測組合(IMU，下文簡稱慣組)用于給導彈、飛機、車輛等提供姿態、位置信息等以實現導航功能。其內部一般安裝用于測量的敏感器件，包括線性加速度測量敏感器件-加速度計。

導彈在飛行過程中，因彈體迎角、彈體翻轉、空氣舵操控、噴管擺動等原因，導致全彈因氣動力和慣性力等原因產生振動。隨著結構傳遞，彈體的動態載荷在慣組安裝面形成新的動態激勵。一方面，動態激勵量級過大直接影響加速度計的測量精度；另一方面，受激勵作用，因結構原因產生的線角耦合使得加速度計的測量值無法準確表征彈體導航基準的實際參數。

國內外對彈載慣組的減振性能已經進行了部分研究。文獻[1]對全彈的振動響應進行建模與分析；文獻[2]對慣組加速度計振動響應進行了動力學推算；文獻[3-4]對材質均勻狀態下的慣組減振布局進行了動力學推導，對線角耦合產生的機理進行了初步分析；文獻[5]對MEMS慣組內部結構進行振動環境的動力學建模；文獻[6-8]介紹了常用橡膠減振墊材料特性、減振墊構造及減振性能；文獻[9-12]提出了多種基本結構的振動響應分析方法。

現有文獻對彈體和慣組單獨進行了動力學建模分析，但是未能將彈體和慣組作為整體系統進行分析。本文構建了彈體-慣組的兩自由度動力學分析模型，配合仿真手段，研究了減振墊剛度等因素對彈載慣組振動響應的影響機理。現有文獻探究了慣組為理想剛體情況下，慣組質心偏心引發線角耦合的機理，但是未能研究慣組內部架構應變導致的線角耦合，未能將研究對象細化到加速度計等傳感器件的布局。本文研究了慣組內部架構固有頻率特性以及加速度計布局對振動響應的影響機理。同時基于上述研究提出對應的優化設計準則。

1 全彈結構因素的影響機理

為保證加速度計在振動環境下的測量精度，慣組通常通過減振墊安裝于彈體的安裝支架上。通過減振墊材料選取以及減振墊的尺寸設計等途徑可以調節減振墊的剛度，達到優化加速度計振動響應的目的。用作減振墊的硅橡膠的彈性模量接近3～5 Mpa,部分天然橡膠的彈性模量能夠低至0.5 Mpa。

為實現優化加速度計振動響應的目的，需要研究減振墊剛度等因素對加速度計振動響應的影響。加速度計振動響應并非隨著減振墊剛度的降低而一直降低。例如某型慣組采用5種彈性模量的減振墊進行振動性能摸底，得到數據如表1。實驗表明該型慣組使用彈性模量為1.5Mpa減振墊時的加速度計振動精度比用1.0Mpa減振墊好。

表1 加速度計振動精度實驗數據

針對上述慣組及對應彈體結構構建分析模型。設定全彈特征狀態包括彈體空載狀態、彈體滿載狀態。彈體空載狀態只包括彈體殼體和主要支撐構件，彈體滿載狀態包括彈體殼體、主要支撐構件和慣組等負載。

上文已對彈體振動的激勵因素進行闡述。對于帶擺動噴管的導彈，發動機引發的隨機振動占主要因素。以彈體結構遠離慣組一端模擬發動機噴管在彈載發動機上的安裝面，隨機振動激勵作用于該面。

將空載彈體和彈載慣組簡化為一個兩自由度系統，如圖1。其中空載彈體質量為m1，彈體殼體和支撐架構的整體剛度為k1，慣組質量為m2，慣組減振墊和慣組支撐架構的整體剛度為k2。外部激勵為正弦激勵，幅值為J，頻率為w。

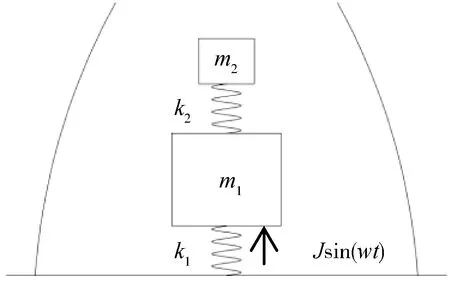
圖1 空載彈體和慣組的兩自由度模型

設定空載彈體的位移為x1，慣組的位移為x2，則系統運動微分方程為。

(1)

(2)

構建三維分析模型。定義全彈的坐標系和慣組坐標系重合，彈體主軸指向發動機噴管安裝面一側為Z軸正向，慣組安裝面垂直于Z軸，X軸和Y軸分別沿慣組減振墊構成的正方形兩側邊的方向，X軸、Y軸和Z軸構成右手坐標系，如圖2。

慣組采用4對減振墊，每對減振墊的2個墊子沿X0Y平面對稱，減振墊幾何中心在X0Y平面的投影呈正方形布置。定義上述正方形的幾何中心為慣組的減振中心。按照導彈設計的通用狀態，該模型慣組減振中心位于彈體中心軸。構建模型使得慣組的質心和減振中心重合，且加速度計組合幾何中心與慣組減振中心在X0Y平面的投影重合。加速度計組合包含3個安裝面法線方向分別沿X軸、Y軸和Z軸的加速度計，3個正交加速度計軸線穿過加速度計組合幾何中心，該模型加速度計組合幾何中心到慣組減振中心的距離為(0 mm,0 mm,24.5 mm)。彈體模型如圖2所示，慣組模型如圖3所示，安裝配重件，使慣組質心和慣組減振中心重合。圖3除去減振墊的部分稱為本體組合。

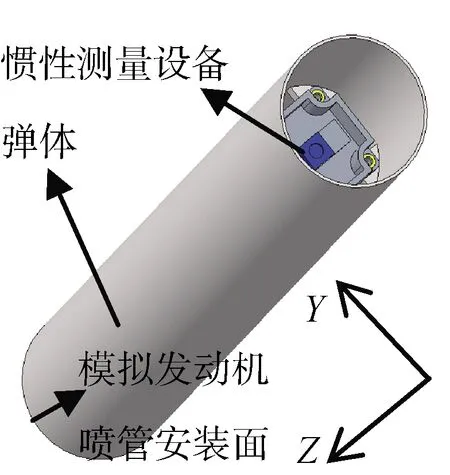
圖2 彈體模型示意圖

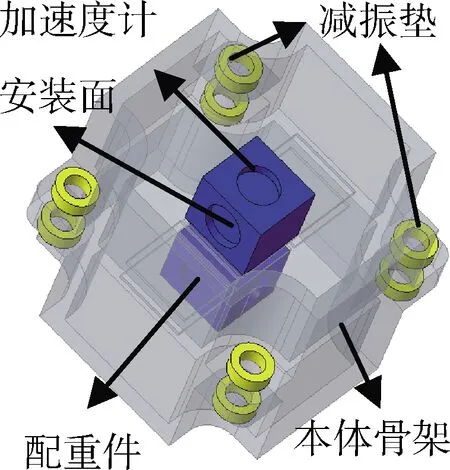
圖3 慣測組合示意圖

輸入激勵為隨機振動，參數如表2。彈載慣組用減振墊材質為橡膠材質，該類材料在應變量級小的情況下，彈性模量近似不變。經過仿真分析，得到的響應數據如表3。

表2 輸入激勵數值

表3 慣性導航設備與全彈固有頻率關系研究仿真結果

定義沿系統X、Y、Z方向的線性運動分別為UX、UY、UZ；繞X、Y、Z軸的轉動分別為RX、RY、RZ。

繪制狀態1～5加速度計的振動響應量級，如圖4。

圖4 五種狀態響應量級趨勢曲線

圖4的數據表明隨著減振墊彈性模量的降低，加速度計的振動響應總體呈減小趨勢，唯獨狀態4加速度計振動的響應比狀態3高。狀態3和狀態4的前7階模態分別如表4和表5。圖5～圖6為狀態3和狀態4中X向振動X加速度計的響應譜。

表4 狀態3彈體滿載前7階模態

表5 狀態4彈體滿載前7階模態

如圖5～圖6所示，狀態4基頻響應峰值仍然低于狀態3，但二階頻率峰值高于狀態3，且二階頻率峰值區間寬度大于狀態3。經過分析，狀態3的二階頻率對應第5階模態，而狀態4的二階頻率與第5階模態和第7階模態對應的頻率均非常接近。狀態4第5階模態和第7階模態響應分別如圖7～圖8所示。

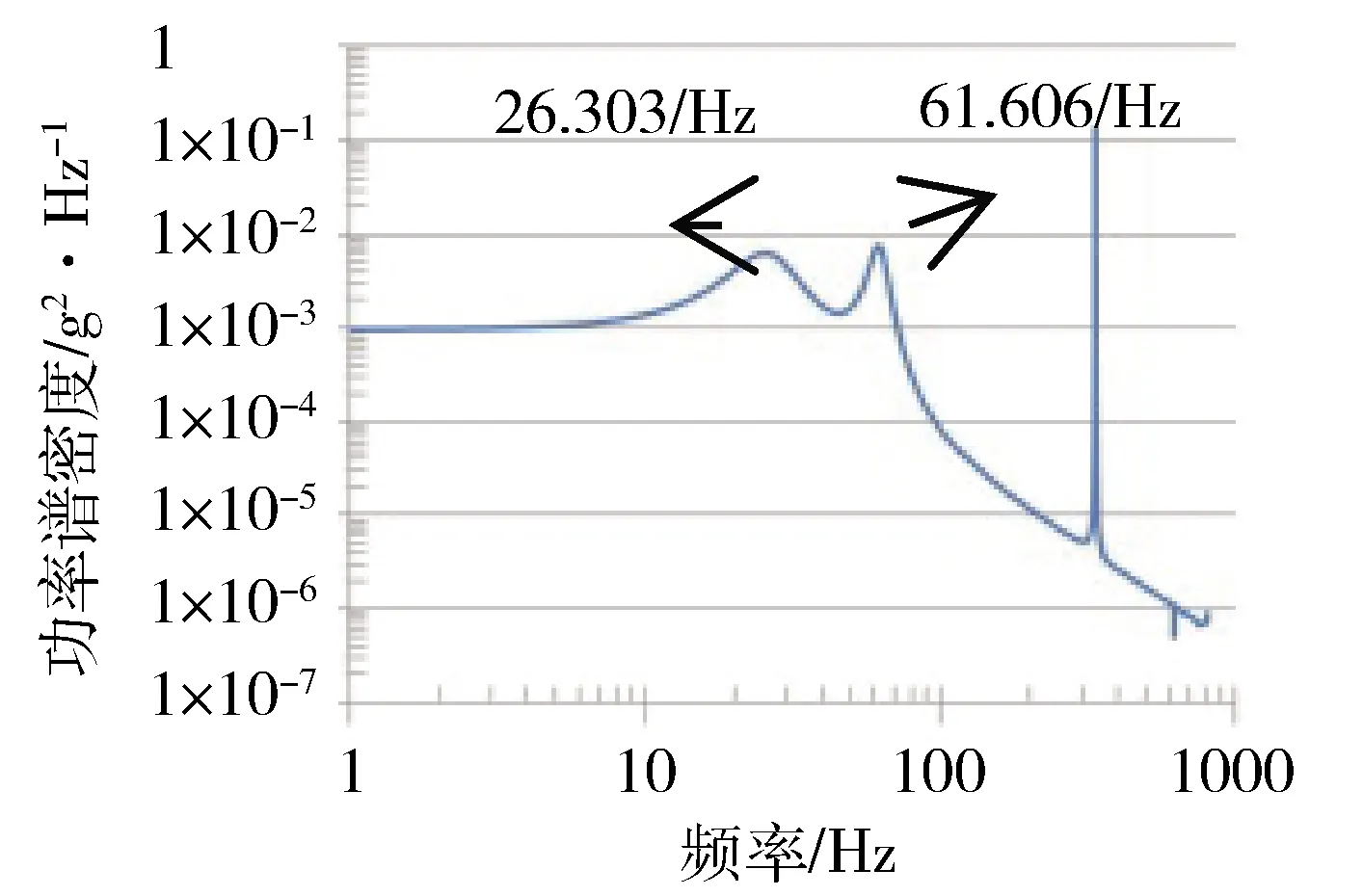
圖5 狀態4響應

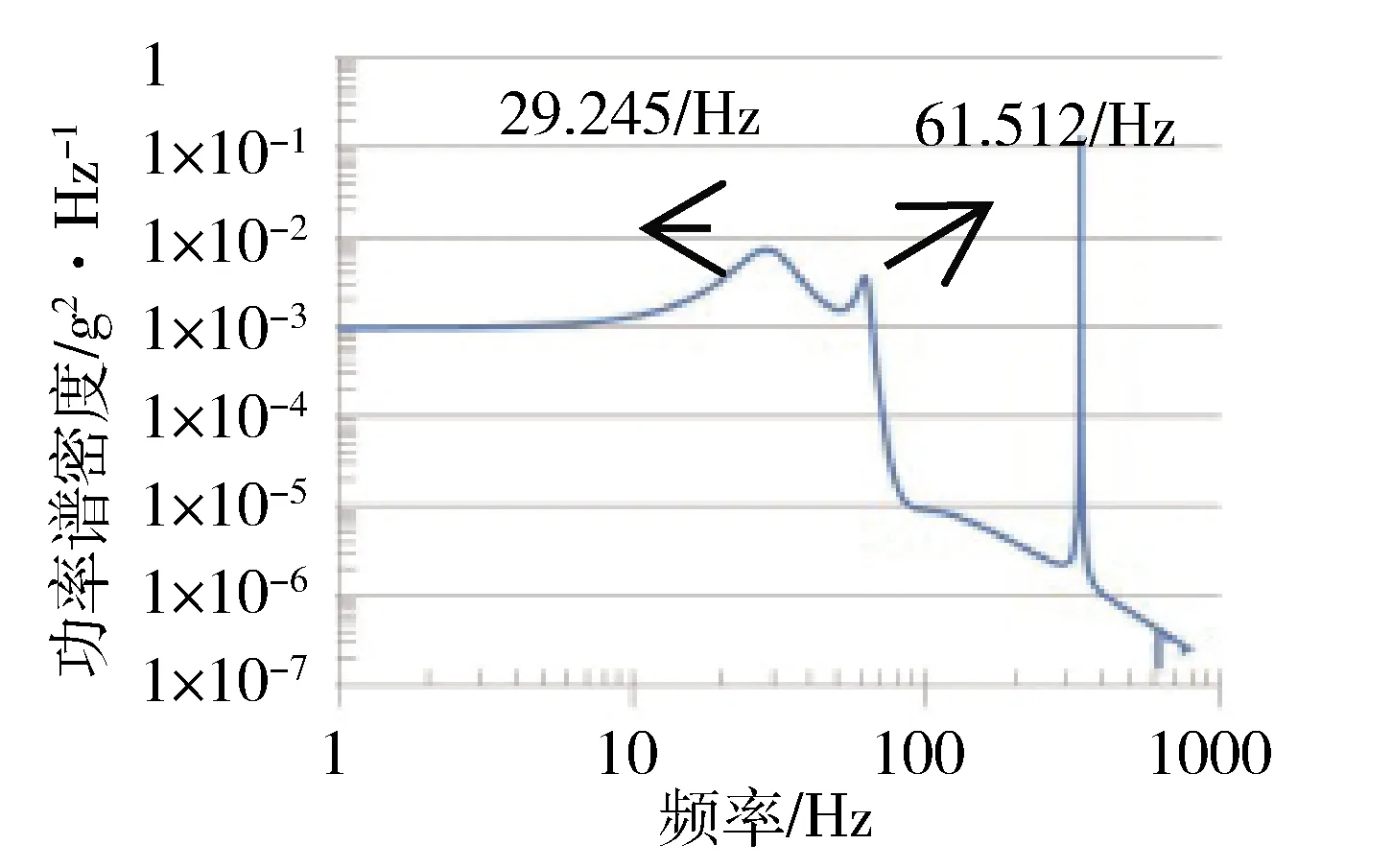
圖6 狀態3響應

圖7 狀態3-4第5階模態

圖8 狀態3-4第7階模態

狀態4第5階模態自由度為RY，發生頻率為59.74 Hz；第7階模態自由度也是RY，發生頻率為62.15 Hz。兩階頻率接近，且對應自由度一致，造成對應頻率響應峰值增大，峰值范圍變寬。

針對上述問題，基于式(1)和式(2)，依據動力學原理推算可以得到。

(3)

(4)

式中，wn1,2分別為兩自由度系統的一階、二階固有頻率；B為慣組響應幅值。

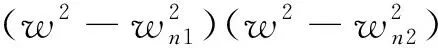
(5)

對于簡單的彈體模型，可以估算彈體剛度和慣組剛度，避免慣組剛度接近式(5)計算值。對于復雜的彈體模型，需要通過仿真分析來避免系統的兩階頻率過于接近。

通過上述分析，慣組和空載彈體在激勵方向構成一個兩自由度系統。隨著減振墊剛度降低，加速度計的振動響應呈減小趨勢。但是上述兩自由度系統在外部激勵方向上的兩個固有頻率過于接近時會產生慣組響應突增的現象，需要通過設計分析來避免。同時，設計時需要注意減振墊剛度過低，如部分天然橡膠減振墊，只能適用于中低頻低量級振動環境，否則面臨大量級載荷作用下損壞的危險。

2 慣組內部結構因素的影響機理

工程實踐證實，慣組內部結構因素對加速度計的振動響應存在顯著影響，包括本體骨架剛度、慣組質心到慣組減振中心的距離等。為重點分析上述因素對加速度計振動響應的影響規律，構建仿真模型。通過調節本體骨架的彈性模量以及材料厚度等方法均勻改變本體骨架剛度；通過增減配重件、調節加速度計的位置達到調節慣組質心到慣組減振中心距離的目的。

定義圖3所示的慣組狀態為理想質心狀態。圖9所示慣組在圖3基礎上取消配重件,將加速度計安裝位置向-X向移動50mm，定義該狀態為質心偏心狀態，對應狀態的質心偏心量如表6。

表6 質心偏心狀態慣組沿三軸方向的偏心量

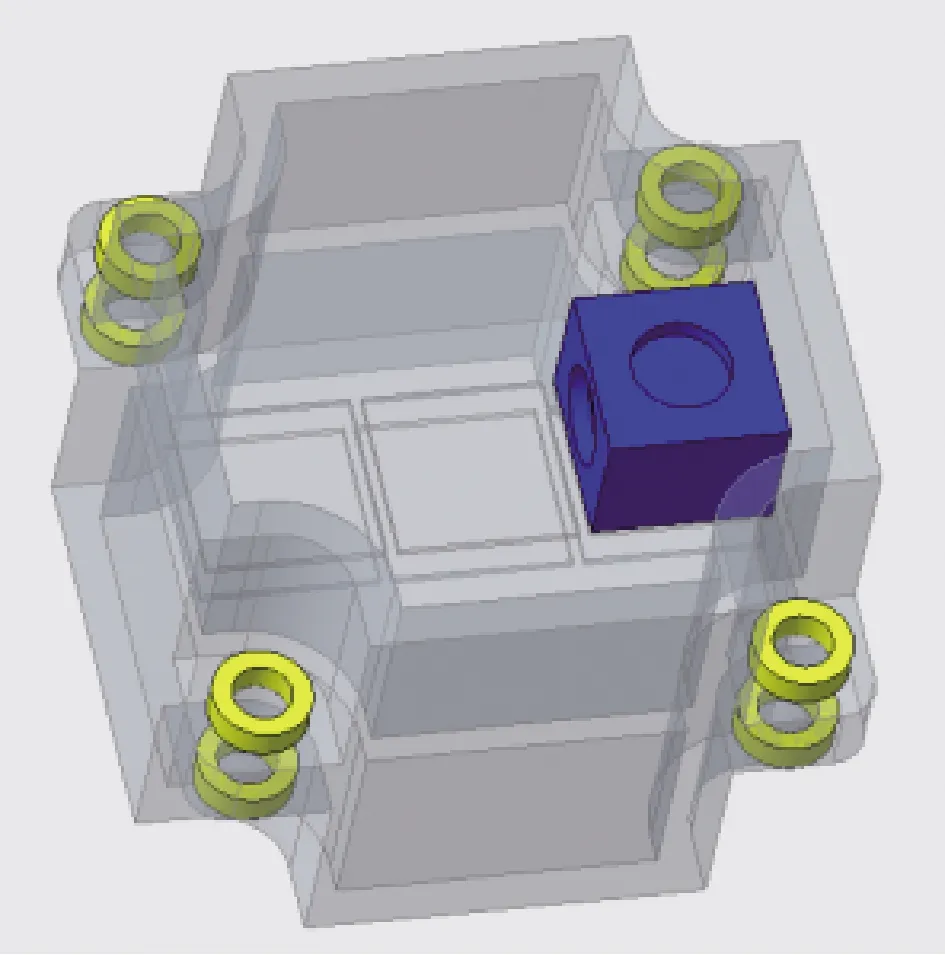
圖9 質心偏心狀態

調節慣組內部結構參數，確定4種狀態，分別進行仿真計算，仿真結果如表7。

根據表7數據，可以發現如下現象：

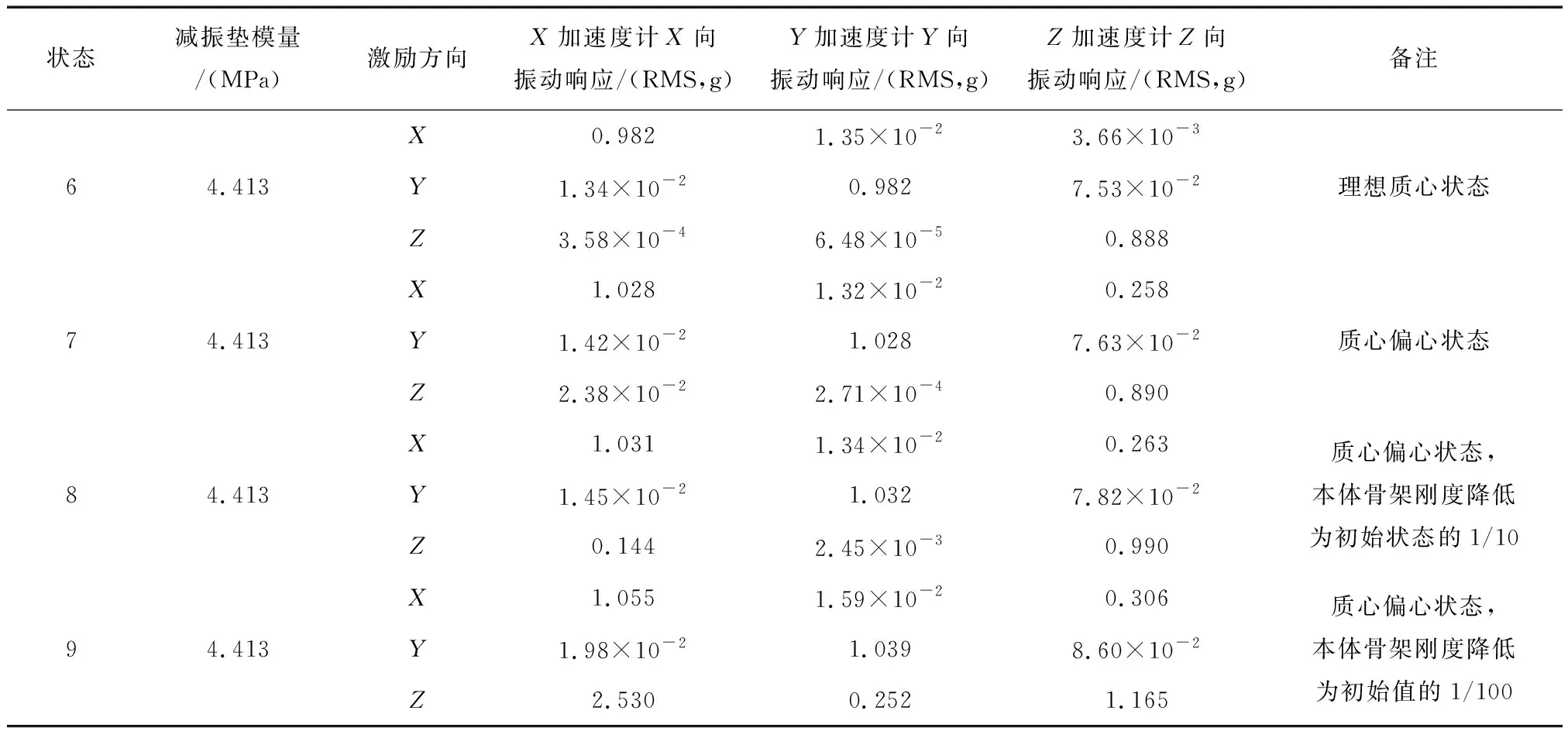
表7 慣組內部因素對加速度計振動響應的影響機理研究仿真結果

1)狀態7相較于狀態6，激勵方向為X向時，Z加速度計Z向的振動響應量級明顯增加，由3.66×10-3g增加到0.258g。

2)隨著本體骨架剛度的降低，加速度計的振動響應量級均有提升。

3)狀態9相較于狀態7，激勵方向為Z向時，X加速度計X向振動響應量級變化明顯，由2.38×10-2g增加到2.530g。

分析現象1。因質心偏心，激勵方向為X向時，慣組產生了RY向的角運動。同時因為Z加速度計到慣組減振中心存在沿UZ方向距離分量，即如圖10所示的LZ值，導致角運動引發Z加速度計Z向的線性運動。

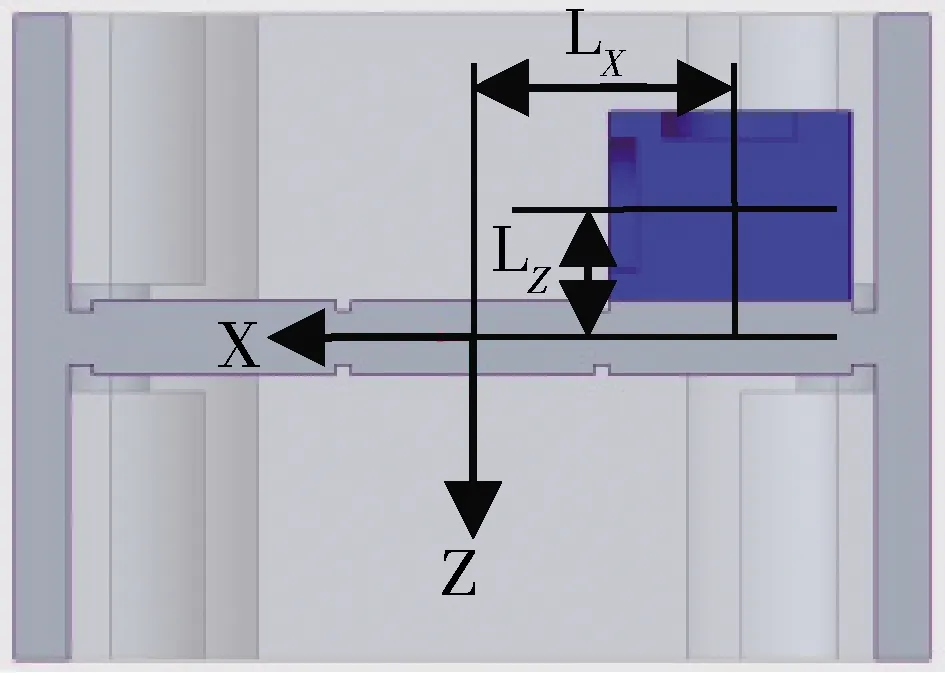
圖10 加速度計位置參數

現象2表明與減振墊剛度的影響相反，本體骨架剛度越小，加速度計響應越大。

分析現象3。圖11為狀態9中Z向振動X加速度計X向響應曲線。

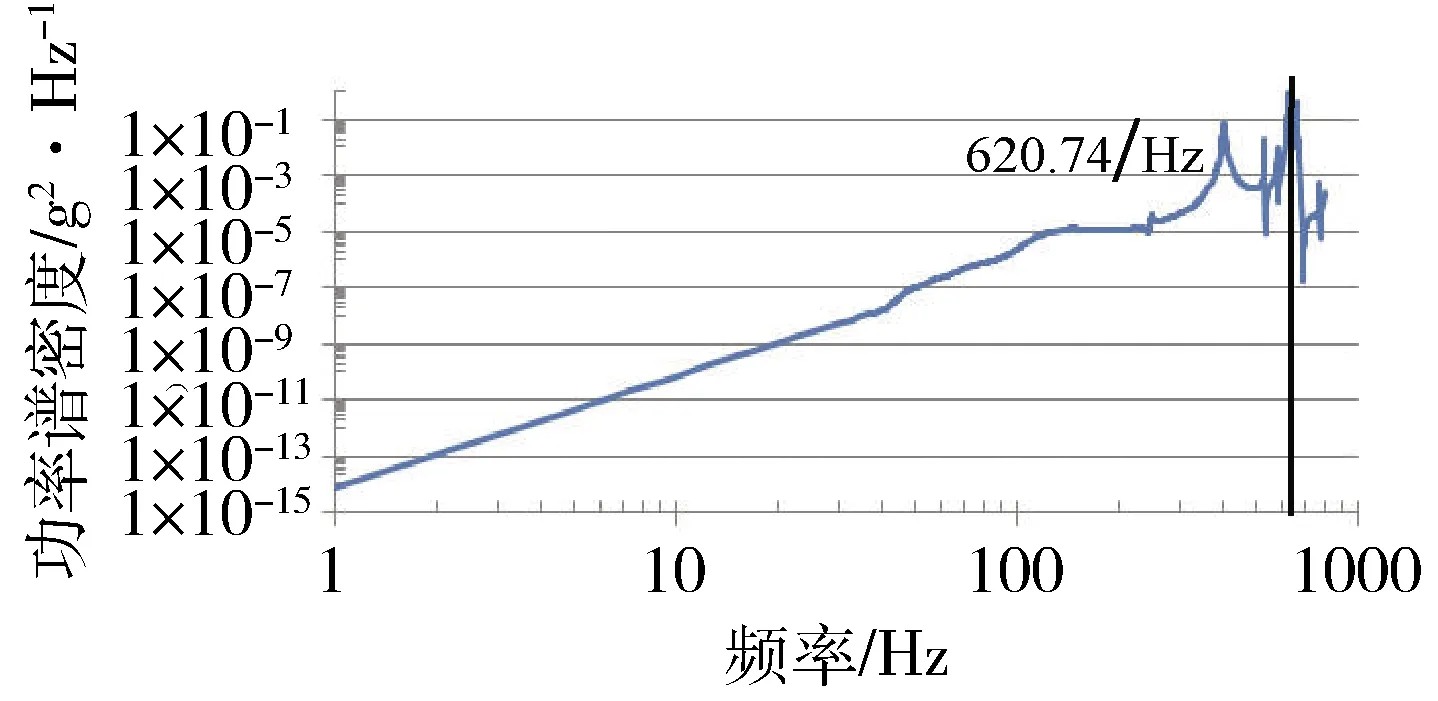
圖11 Z向振動X加速度計X向響應曲線

通過圖11可以發現，加速度計組合在350 Hz～800 Hz頻段出現高量級響應，其峰值響應頻率對應的模態如圖12～13。

圖12 全彈峰值響應模態

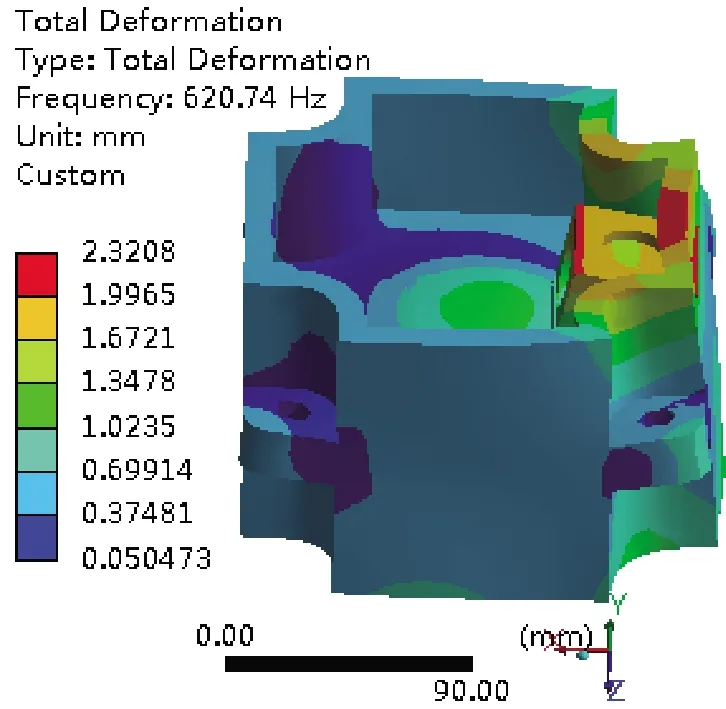
圖13 本體組合耦合模態

圖12～13可見，因為本體骨架的應力變形，加速度計組合在620.74Hz處產生了RY向和UZ向運動的耦合，是產生現象3主要原因。分析狀態9本體組合的模態響應,800Hz以下有18階模態。而狀態7本體組合1階模態為3778.2Hz超出激勵頻段范圍；狀態8本體組合1階模態為1213.3Hz，同樣超出激勵頻段范圍。單獨分析狀態9本體組合，620.74Hz接近其第9階模態，對應自由度為RY+UZ。

基于上述分析，可以歸納慣組內部結構的振動性能優化設計準則。

1)設計保證慣組質心盡量接近慣組減振中心。存在質心偏心時，減小加速度計到慣組減振中心在垂直于激勵方向的距離，能夠減小線角耦合導致的加速度計測量誤差。

2)優化結構剛度，保證慣組本體組合的基頻盡量高于外部激勵的最高頻率。當結構設計難以實現前述目標時，通過仿真分析，確定本體組合的線角耦合頻率，設計優化需使得該頻率高于外部主要激勵的最高頻率。

3 結 論

針對彈載慣組加速度計振動環境下的測量精度超差問題，從全彈結構和慣組內部結構兩方面因素進行分析研究。基于工程實例，構建分析模型。將全彈模型簡化為空載彈體和慣組的兩自由度系統，通過動力學推導，研究了慣組剛度對慣組振動響應的影響規律；構建仿真分析模型，研究減振墊剛度、本體組合剛度、質心偏心量、加速度計到慣組減振中心距離等因素對振動環境加速度計測量精度的影響，并提出優化設計準則。