視線制導坐標系下空間自主交會故障診斷與容錯控制集成設計

劉偉杰 陳 斌 馮佳佳

1. 北京控制工程研究所，北京100094 2. 空間智能控制技術重點實驗室，北京100094

0 引言

20世紀末以來，空間自主交會對接技術得到了越來越多的應用。在自主交會最終逼近段的接近軌跡設計及其相對應的故障診斷、隔離與恢復，被認為是自主交會最主要的技術難點[1]。在這一階段，追蹤航天器可能受到帆板的撓性運動、液體晃動等干擾，另外還因為軌道攝動、各種導航和控制誤差、推力器故障等原因，導致實際軌跡與計劃軌跡之間會產生偏差[2]，這也增加了追蹤航天器故障診斷的難度。目前對于推力器故障的容錯設計主要是針對被動軌跡保護和主動軌跡保護兩大類方法[2-3]。采用解析模型故障診斷與容錯控制的思想研究這一問題的文獻還比較少見[4-5]。針對航天器圓軌道自主交會問題，劉偉杰在考慮推力器輸出約束的情況下，完成了故障診斷與容錯控制的集成設計[6]。需要注意的是，航天器自主交會過程中追蹤航天器一旦發生故障，就需要航天器在極短的時間內完成故障的診斷與隔離，否則航天器會偏離規劃軌跡，而這往往意味著交會任務的中止。

近年來，故障診斷與容錯控制集成技術由于其高可靠性及兼顧診斷性得到了越來越多的關注。Nett首先提出了故障診斷與容錯控制集成設計思想[7]，并設計了一個四參數集成控制器。陳雪芹針對航天器執行機構和敏感器故障，考慮故障診斷結果的不確定性與系統參數的不確定性，分別采用H2和H∞范數作為系統故障診斷和容錯控制的性能指標，設計輸出反饋混合H2/H∞控制律[8]。Fan J H在考慮執行機構飽和限制的情況下，設計了一種魯棒集成方法[9]，并在無人機控制系統中得到了應用。Wang H[10]針對線性變參數系統以及帶有不確定性的線性離散系統，設計了故障診斷與容錯控制集成方法，但這兩種設計方法只能針對低頻故障，對于高頻干擾也缺乏魯棒性，對于快變故障難以達到診斷與容錯目的。Zhang Ke在其專著[11]中研究了非線性系統的故障診斷與容錯控制的集成設計，但沒有考慮建模不確定性的問題，并且采用一致終極有界理論證明觀測器的穩定性，使得該方法的實用性受到很大限制。Davoodi[12]針對線性切換系統，在H∞/H2框架下設計了故障診斷與容錯控制的集成設計，并通過求解線性矩陣不等式得到系統參數。

本文針對視線制導坐標系下自主交會的軌道控制問題，考慮推力器故障，研究了一種故障診斷與容錯控制的魯棒集成設計方法。

1 故障診斷與容錯控制集成設計

1.1 問題描述

實際交會過程中的最終逼近段，追蹤飛行器和目標飛行器一般已經處于同一軌道平面內，因此最常用的是兩個飛行器在同一軌道平面上的動力學方程。文獻[13]給出了任意偏心率軌道上的視線相對運動方程:

(1)

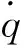
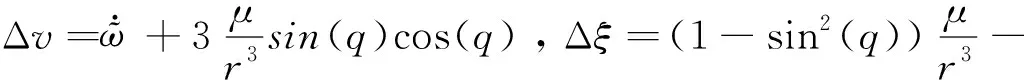
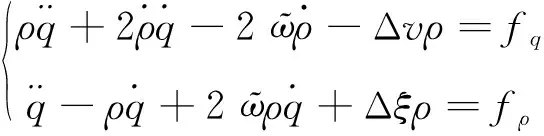
(2)

方程(2)的第1行為視線方向的運動方程,稱為縱向運動方程。第2行為視線垂直方向的運動方程,稱為法向運動方程。

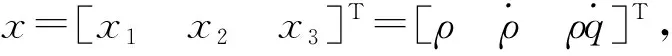
(3)

這是一個含有建模不確定型的非線性系統，

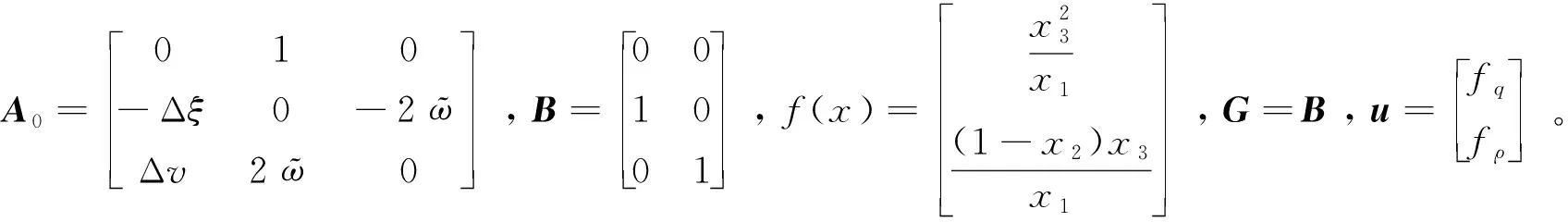
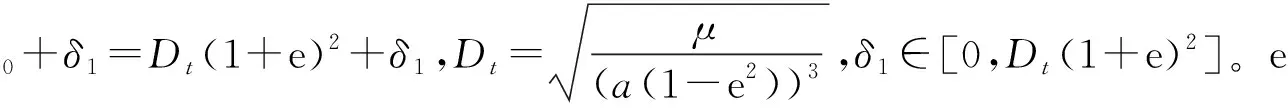
A0=A+ΔA

(4)

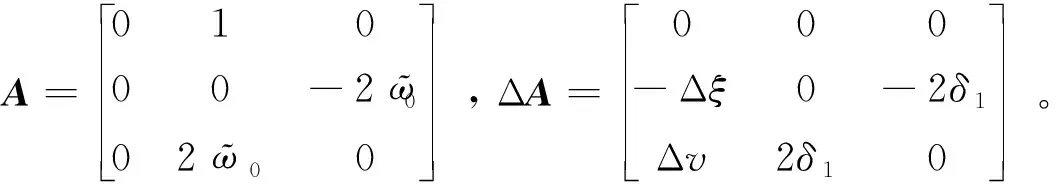
動力學方程(2)的不確定性部分ΔA又可以表示為

ΔA=EΔΔFΔ

(5)

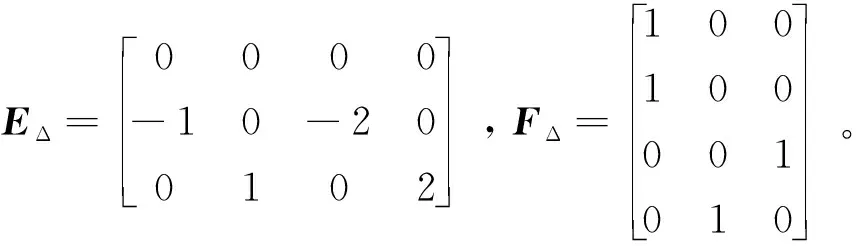
在考慮推力器故障的情況下，動力學方程(2)可以表示為

(6)

式中fa(t)表示推力器故障矢量，E為推力器故障輸入矩陣，且E=B，C為系統狀態的觀測矩陣，y為系統狀態輸出。

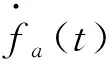
1.2 魯棒容錯控制器設計

對于方程(6)設計故障觀測器

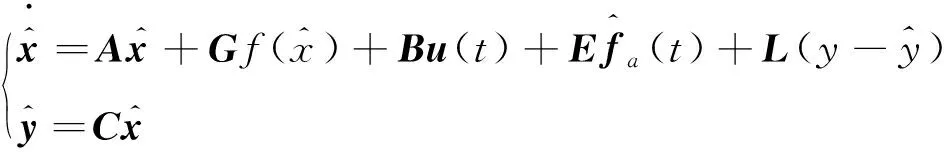
(7)

(8)

(9)

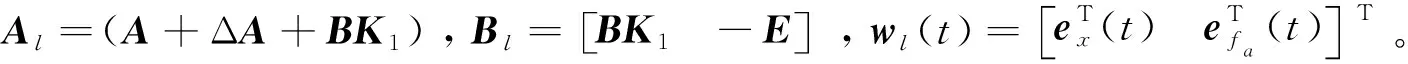
取Zl=Clx，Cl=I作為廣義可控輸出。則可以得到一個廣義線性不確定性系統

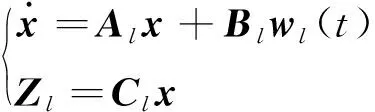
(10)

引理1[14]對于不確定性系統(10)，假設γ1>0是任意給定的常數，則下列2個條件是等價的：

2)存在一個正定矩陣P1，使得下列不等式成立：

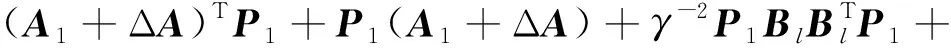
(11)

式中A1=A+BK1。

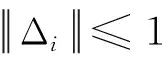
(12)

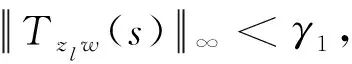
(13)

式中R0=AX+XAT+BW1+(BW1)T，W1=K1X。

(14)

根據schur正交補定理，式(14)等價于不等式(12)，根據引理1和引理2即可得到定理1中的結論。

1.3 自適應故障觀測器設計

設計推力器故障的自適應估計律為

(15)

則系統(10)的狀態估計誤差為：

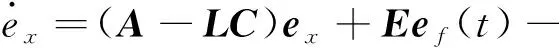
(16)

故障估計誤差的動態方程：

(17)

(18)

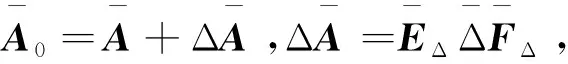
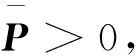
為了分析廣義系統(18)的穩定性情況，首先定義一個橢球集并引入兩個引理：

(19)

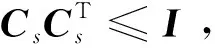
引理4[17]設xs和ys為具有適當維數的向量，則下列不等式成立：

式中Qs是任意具有適當維數的正定矩陣。

(20)

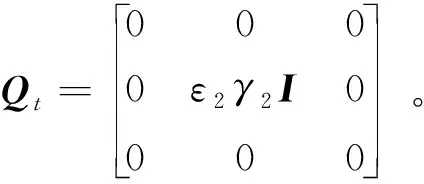
證明. 定義一個Lyapunov函數

(21)

求它對時間的導數可以得到

(22)

(23)

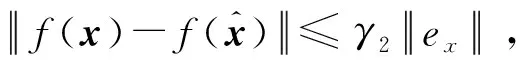
上式又可以表示為：

(24)

結合式(22)～(24)，可以得到

(25)

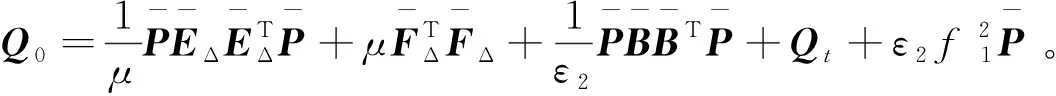
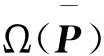
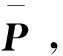
(26)

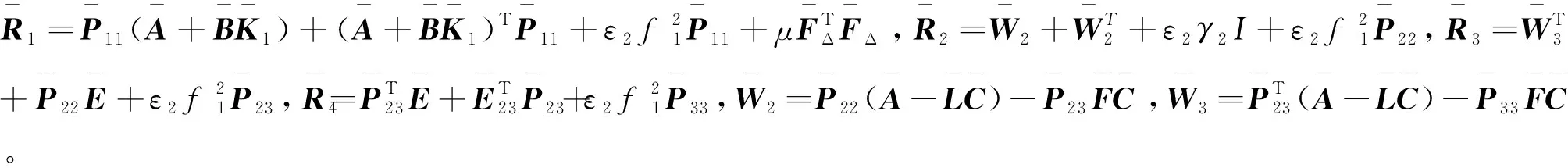
證明.與定理1的證明高度類似，此處省略。

根據定理3可以得出，不確定性系統(10)的狀態估計誤差ex和故障估計誤差efa是收斂有界的。從而故障觀測器的參數可以由下式求得

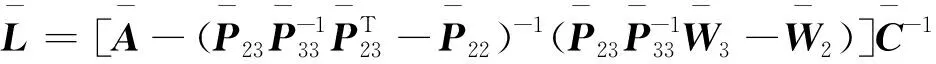
(27)

2 仿真結果

根據定理3，可以求得觀測器的參數為：

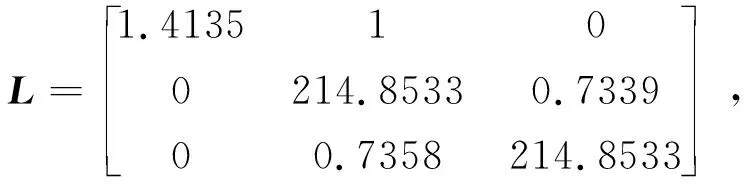
仿真結果如下圖所示。圖1是無故障發生時，追蹤航天器的相對位置變化曲線，可以看出交會過程是穩定的，并且沒有超出測量視場等情況發生。

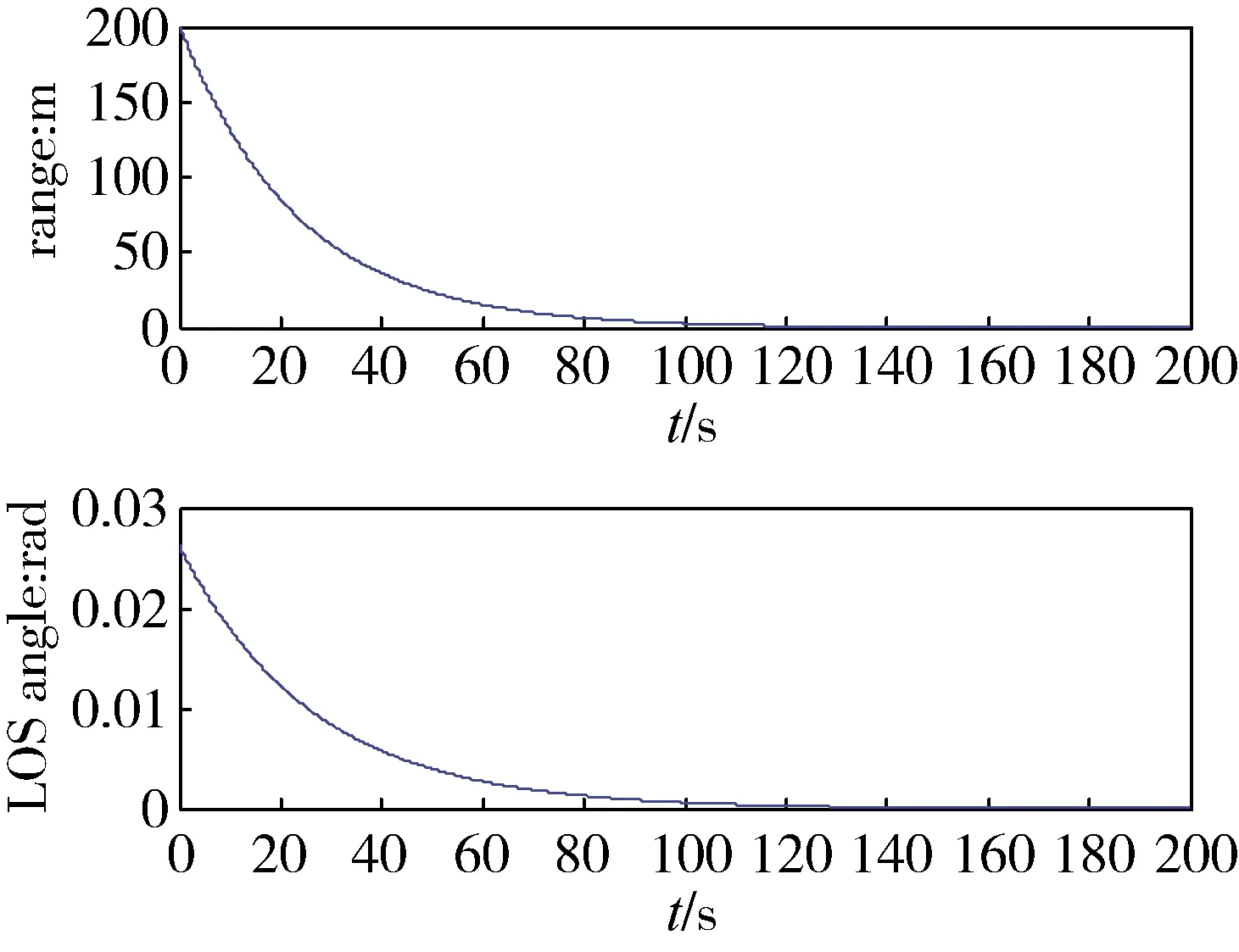
圖1 目標航天器和追蹤航天器的相對位置

為了更清楚地說明航天器在交會平面內的相對軌跡，本文采用國際空間站的逼近走廊進行說明。

如圖2所示，在距離目標星200m～20m之間，逼近走廊以V-bar為中心線，半錐角為8°，在最后20m，逼近走廊以“對接單元口平面”縱軸為中心線，半錐角為4°，圖2是無故障發生時的相對軌跡。

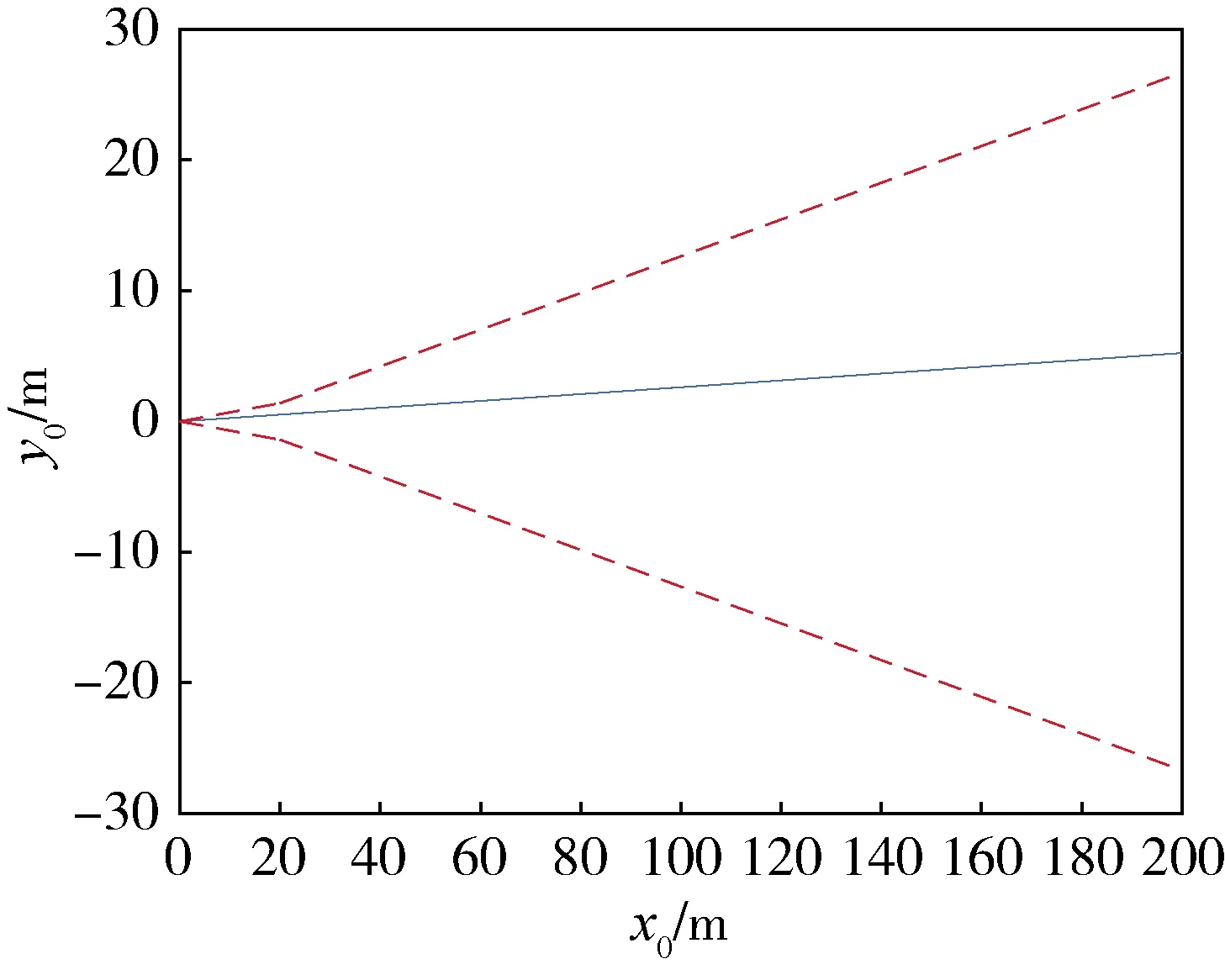
圖2 追蹤航天器沿逼近走廊的相對軌跡

圖3是推力器真實故障與故障觀測器的輸出曲線，從圖中可以看出，故障觀測器的輸出結果與仿真設定值一致。

圖3 故障觀測器對追蹤航天器故障的觀測結果

假設追蹤航天器推力器在10(60s之間發生故障，故障函數用fq=(-0.05sin(0.05πt)-0.05)m·s-2表示。追蹤航天器在逼近走廊中的相對軌跡如圖4所示。

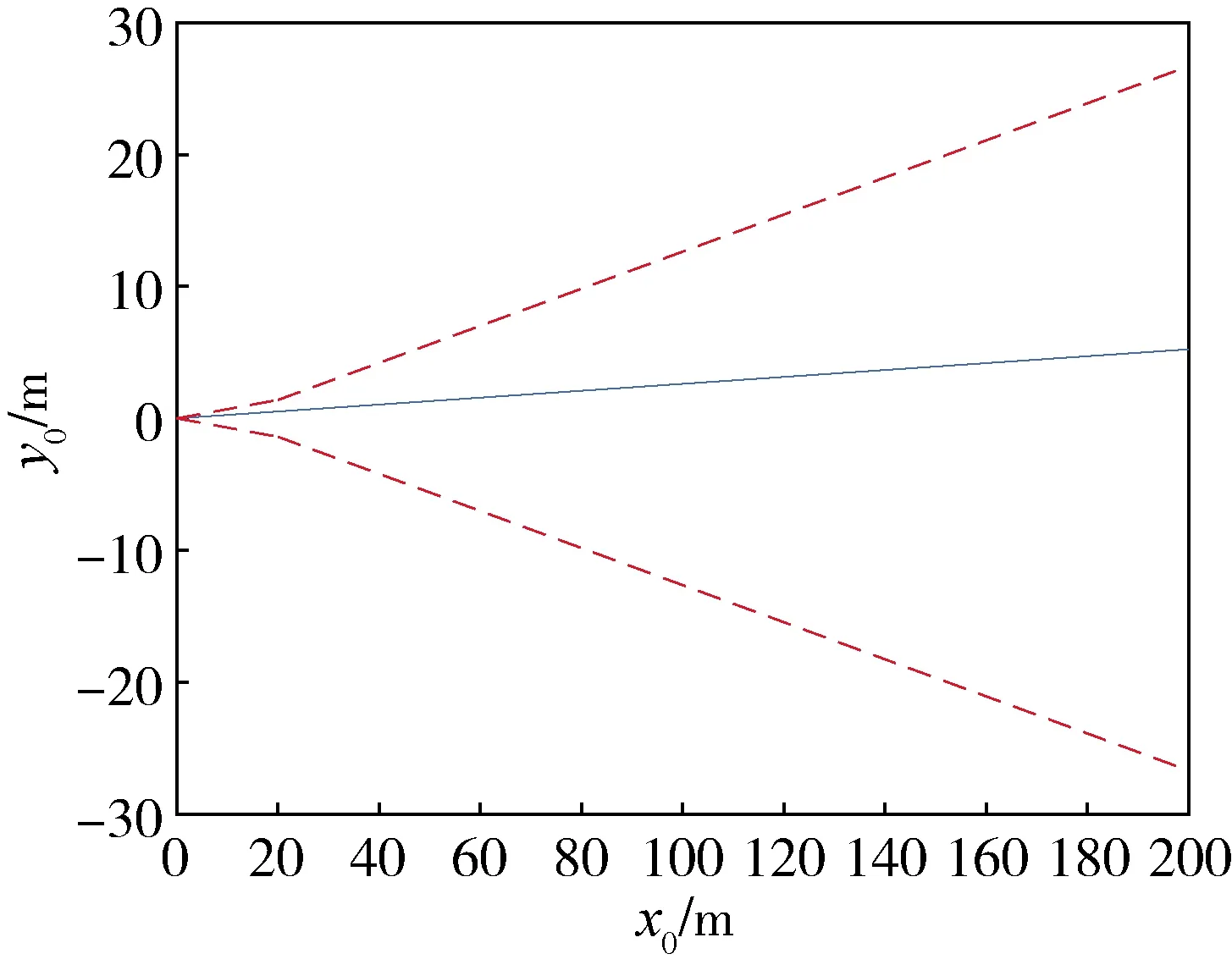
圖4 故障情況下追蹤航天器沿逼近走廊的相對軌跡

從圖中可以看出，追蹤航天器沿逼近走廊的軌跡控制仍然令人滿意，在故障條件下，追蹤航天器沒有超出視場或觸發避撞機動等情況，為追蹤航天器在不影響交會任務的前提下，實現故障單機隔離并切換備份，達到了容錯控制的效果。

圖5是推力器真實故障與故障觀測器的輸出曲線，從圖中可以看出，追蹤航天器推力器發生故障后，故障觀測器迅速并準確地估計出故障，估計結果與仿真設定值基本一致。

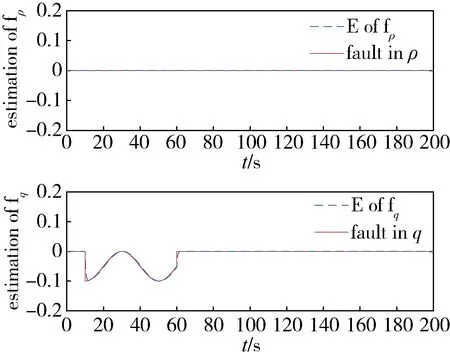
圖5 故障觀測器對追蹤航天器故障的觀測結果

3 結論

對于視線制導坐標系下的自主交會問題，本文設計了故障診斷與容錯控制魯棒集成方法。該方法構造簡單，便于實現，在追蹤航天器發生推力器故障后，能夠在保證追蹤航天器軌跡安全的同時，迅速準確地診斷并隔離故障。該方法能夠提高空間交會的安全性，減少避撞機動等操作的風險，從而提高自主交會的成功率。