初中數學教科書中“幾何直觀”的設計類型及原則

顧繼玲，章 飛

初中數學教科書中“幾何直觀”的設計類型及原則

顧繼玲1，章 飛2

（1．南京師范大學 教師教育學院，江蘇 南京 210097；2．江蘇第二師范學院 課程與教學研究所，江蘇 南京 210013）

幾何直觀兼具認識論和方法論兩方面的教育價值．初中數學教科書中幾何直觀的類型有直觀表征、直觀分析、直觀解釋和直觀發現．初中數學教科書幾何直觀的設計應遵循以下原則：準確性，既是知識工具更是能力素養；整體性，兼顧內容和類型避免出現偏差；漸進性，問題表述的類型和圖形的明晰程度要有層次；反思性，要有反思性的問題和活動．

初中數學；教科書；幾何直觀；類型；原則

1 問題提出

“幾何直觀”是《義務教育數學課程標準（2011年版）》提出的在數學課程中應當注重的十個核心概念之一，《高中數學課程標準（2017年版）》也將“直觀想象”列為6個學科核心素養之一，“直觀想象素養整合了空間想象、幾何直觀和空間觀念”[1]，是在“幾何直觀”基礎上更進一步的要求．當前對“幾何直觀”或“直觀想象”的相關研究并不少，但從研究內容來看，更多涉及學生學習或教師教學，對教科書中幾何直觀的呈現或設計研究很少．教科書作為學生學習內容的主要載體，自然應做好為學生提供發展幾何直觀素養的學習材料，為學生的學習和教師的教學做好價值引領，因此教科書中“幾何直觀”的設計顯得尤為重要．研究首先分析幾何直觀的教育價值，在此基礎上試圖以初中數學教科書為例，對教科書中幾何直觀呈現的基本類型及教科書幾何直觀設計的原則等方面進行探討．

2 幾何直觀的教育價值

幾何直觀能做什么？有哪些基本類型？教科書如何滲透幾何直觀？等問題，都應建立在幾何直觀教育價值的基礎之上，因此在討論教科書設計問題之前依然需要分析幾何直觀的教育價值．

“幾何直觀主要是指利用圖形描述和分析問題．借助幾何直觀可以把復雜的數學問題變得簡明、形象，有助于探索解決問題的思路，預測結果．幾何直觀可以幫助學生直觀地理解數學，在整個數學學習過程中都發揮著重要作用”[2]，對幾何直觀的內涵和作用，《義務教育數學課程標準（2011年版）》給出的上述論述是廣義的、概括的．這里的“圖形”含義也是廣義的，不僅僅局限于幾何圖形，包括常見的平面圖形、立體圖形以及數軸、坐標系、表格、框圖、直觀素材等，解決的問題也不限于數量關系．

選取涉及幾何直觀的教育價值、意義或功能的有代表性的文獻，對其進行梳理歸類，可歸為兩個方面．

一是認識論方面，很多重要的數學內容、概念都具有“雙重性”，既有“數的特征”，也有“形的特征”，是認識數學對象的兩個基本角度，要用數和形“兩只眼睛”看數學，只有從兩個方面認識它們，才能很好地理解它們、掌握它們的本質意義．相關論述諸如，幾何直觀是認識論問題，是認識的基礎，有助于學生對數學的理解，借助于幾何直觀、幾何解釋，能啟迪思路，可以幫助我們理解和接受抽象的內容和方法[3]，數學的發展過程也表明，再抽象的數學結論總能找到相對直觀的表征和解釋……恰當地運用幾何直觀，不僅能更好地建立起數和形之間的聯系、促進相互的轉化，提高綜合運用知識的能力，而且能給學習帶來極大的好處[4]，幾何直觀有助于將抽象的數學對象直觀化、顯性化[5]，幾何直觀具有解釋功能[6]．

二是方法論方面，幾何直觀是思考問題、解決問題的思維方式之一，不僅有助于探索問題解決的思路，同時可以獲得對數學的直觀理解，抓住問題的本質．相關論述諸如，“幾何直觀是一種思維形式，它是人腦對客觀事物及其關系的一種直接的識別或猜想的心理狀態”[7]，“借助于見到的或想到的幾何圖形的形象關系產生對數量關系的直接感知，即可稱之為‘幾何直觀’”[8]，“憑借幾何直觀開展的思維活動，可以成為創新性思維活動的開端”[5]，“幾何直觀是種意識，也是種技能與能力”[9]，“幾何直觀具有發現功能”[6]．

因此，幾何直觀有助于人們認識和理解數學對象，同時有助于人們探索問題、整體把握問題和促進發現．

3 教科書中幾何直觀的類型

研究幾何直觀的教科書設計，自然應分析教科書中幾何直觀的不同類型及其作用意義等．有文獻對教科書中蘊含幾何直觀的內容進行了梳理，得到諸如“借助圖形理解公式”“借助數軸掌握運算”“借助圖形探索性質”等呈現類型，這樣的梳理十分具體，但又是過于零碎了，既難免遺漏又不能形成一些上位的思考，有類似知識點羅列之感，難能遷移應用，也難以給教科書設計者以啟示．此外，這種對已有教科書中幾何直觀呈現類型的梳理，是一種“實然”狀態．作為教科書的設計，應進行“應然”考慮，即需要分析在教科書設計中借助幾何直觀能做什么，實現哪些功能？研究者認為基于上述幾何直觀的教育價值，“幾何直觀”在初中教科書中的呈現類型，主要有以下4種．

3.1 直觀表征

直觀表征，即借助圖形表達數學對象，側重于對數學對象“形”的表達．對于教科書中數學對象的直觀表征，一般包括兩種情況，一是數學對象引入時借助圖形直觀地呈現促進對象形成的素材，二是數學對象引入后借助圖形對其進行直觀表征．

很多數學概念是現實模型的直接反映，兼具“數”和“形”兩方面的特征，為此，在引入這些數學概念時可以首先尋找貼近生活的直觀素材，讓學生基于視覺的觀察初步感知數學對象，如小學階段借助小棒等實物幫助學生認識數的組成、理解計數單位，初中階段借助溫度計引入數軸，借助數軸上點到原點的距離引入絕對值的概念等．在小學階段，實物直觀相對較多，中學階段則以符號直觀、圖形直觀為多．

圖1 一次函數變化規律

3.2 直觀分析

直觀分析，即借助圖形分析數學問題，側重于利用圖形尋求解決問題的思路．有些問題中數量較多、數量關系比較復雜、問題的表述也可能增加了無用或干擾信息等，為此，需要用適當的方式將有關的數量及其關系更好地表示出來，便于基于數量關系建立相應的模型解決問題．此時，圖、表等可直觀、形象地呈現數量關系，將復雜的語言文字轉化成圖形語言，幫助分析問題．

如案例1，基于題目的信息，畫出相應的線段圖，數量關系明顯可見，方程呼之欲出．

案例1[10]：

相關實驗研究也表明了幾何直觀在問題解決中的優越性，如同一數學問題，采用直觀圖示的方式呈現和文字語言的方式呈現，小學生解題正確率在前者方式下明顯高于后者方式下[11]，“直觀表征”縮短了解題路徑，優化了解題方案，它展現的是一種知識之間的‘靈活’聯系，言語與直觀之間的靈活聯系[12]．

另外，對于有挑戰性問題的解決，首先要確定研究思路，利用圖形結構可以展現思維脈絡，幫助理清思路．如初中階段無理數的定義，一般教科書通過面積為2的正方形的邊長探索發現它不是有理數，最終給它命名無理數，并給出定義：無限不循環小數叫做無理數．但為什么它不是有理數就是無限不循環小數呢？怎么說明它一定就是無限不循環小數呢？實質上其中蘊含比較復雜的代數推理：面積為2的正方形邊長是無理數，是什么樣的小數？→難以直接解決，轉而說明熟悉的有理數和小數是什么樣的關系？→發現有理數等價于有限小數或無限循環小數→不是有理數，因此不是有限小數或無限循環小數，即為無限不循環小數．要說清楚這件事直觀圖形（圖2）更能夠清晰展現研究問題的思路，反映對問題的整體思考和邏輯關系的清晰表達．

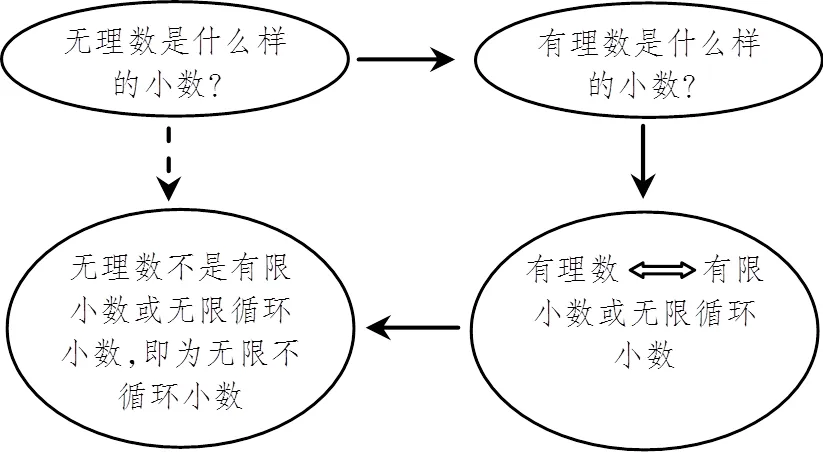
圖2 無理數和小數關系的研究思路

3.3 直觀解釋

直觀解釋，即借助圖形對數學結論或問題的結果進行描述，側重于對已獲得的結果賦予“形”的解釋，從而豐富對數學對象的理解．數學公式可以通過代數運算得到，這是代數思維的體現，但代數公式如能借助圖形進行直觀解釋，可讓代數公式變得形象直觀，便于學生記憶與理解，甚至引發更為一般的推廣，同時也可促進學生思維的發展，促進不同知識內容領域的融合．

案例2[13]：(+)2=2+2+2，你能用旁邊的圖形解釋這個公式嗎？

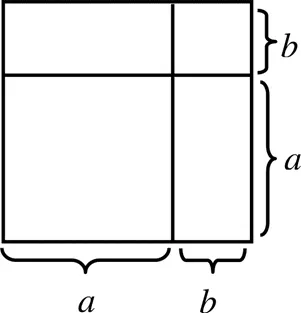
教科書在基于代數運算得到完全平方公式(+)2=2+2+2之后，引導學生借助圖形進行幾何解釋，這樣的解釋形象直觀，而且可引發對于(-)2的猜測，甚至可以引發優秀學生猜想(++)2、(+)3等的幾何解釋和代數表達．

再如，代數運算法則即“算法”本質上是人們發明的一種規則，規則與規律不同，規則反映的不是事物之間內在的必然聯系，它不是客觀存在的．要理解這種人為創造出來的規則并能夠靈活加以運用，首先就要理解規則，了解規則是什么以及為什么，即算理．通過直觀模型為算理提供直觀的解釋，是幫助學生理解算理的常見做法．下面是教科書中有理數加法法則直觀解釋的一個案例——等值相消，運算過程直觀可見．

無論是從事數學教學或研究，我是喜歡直觀的．學習一條數學定理及其證明，只有當我能把定理的直觀含義和證法的直觀思路弄明白了，我才認為真正懂了[8]．代數中的幾何直觀更值得關注，英國數學家阿蒂亞指出，在幾何中視覺思維占主導地位，而代數中有序思維占主導地位．所以幾何中首先用到的是最直接的形象思維，用形象思維洞察，然后用邏輯思維嚴格化．在教育中過分強調一種方式而損害另一種方式是錯誤的[14]．張奠宙先生也表達了相同的觀點，中學代數與幾何課程的主要差別在于代數（包括概念和法則）抽象、繁瑣，而幾何直觀、形象．他因此呼吁，從心理接受能力的角度來說，在代數教學中引入適當的幾何直觀、注重利用貼近生活的形象思維便是代數教學中的一項重要任務．所謂“理解”實際上基本等同于“建立直觀形象”，純粹抽象的事物是難以理解的[15]．

3.4 直觀發現

直觀發現，即借助圖形直觀整體地把握研究對象，發現數學結論．一般有兩種情況：一種是根據要求解或證明的結論構建數學問題的直觀模型，直接獲得問題的解答，另一種是反向的思維過程，即根據直觀圖形發現數學結論．

案例4[10]：將一個邊長為1的正方形紙片分別割成7個部分，部分②是部分①面積的一半，部分③是部分②面積的一半，依次類推．

（1）陰影部分的面積是多少？

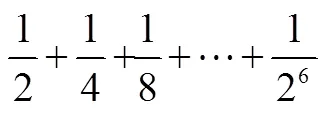
案例5：給出點陣圖，你能發現什么數學結論？觀察可得：圖形直觀表達了數學結論1+3+5+7+9=52，很自然地可以猜想一般結論：

1+3+5+…+(2-1)=2．

直觀發現，往往在獲得問題解答的基礎上可以導致更進一步的發現，對發展學生的直覺思維、培養學生的創新能力提供了空間．如案例4中從代數問題想到如何構造圖形，上述問題中依次“面積的一半”是構造圖形的關鍵點，只要能畫出滿足此條件的圖形即可，因此可以出現另外的構造圖形，如構造線段、三角形、長方形、圓等．案例5中改變“直角形”的構造，又能得到其它熟悉結論嗎？

一個數學對象的幾何直觀對這個對象來說，是種直觀，但對第一次接觸這個直觀方式的學生來說，便可能就是一種抽象[9]．因此，直觀發現需要積累一定的基本圖形的直覺經驗．

另要說明的是，直觀表征、直觀分析、直觀解釋和直觀發現并不完全獨立，直觀分析、直觀解釋和直觀發現都建立在直觀表征的基礎之上，同一個數學問題呈現方式或提出要求不一樣，對直觀類型的側重可能會不一樣，如對平方差公式，如果將直觀圖形作為公式探索的素材，那么圖形的作用主要體現為直觀表征，但如果在獲得公式后要求學生尋求直觀圖形的解釋，那么顯然圖形的作用主要體現為直觀解釋．

4 教科書中幾何直觀的設計原則

教科書的結構（體系）有明線和暗線之分，明線一般為目錄所呈現的具體章節內容，暗線則多隱匿于內容“背后”，如滲透數學思想方法的暗線，培養學生能力的暗線，幫助學生積累數學活動經驗的暗線，幾何直觀作為核心素養也是暗線之一，這種暗線也需一定的內容載體，也需一定的脈絡展現．教科書中幾何直觀的設計應力圖遵循如下幾個原則．

4.1 準確性

教科書中幾何直觀的設計首先要有準確的目標定位，需要明確的是，幾何直觀不僅僅是知識工具，更是能力素養．現有初中數學教科書中各個內容領域利用幾何直觀來處理的教學內容大量存在，如借助數軸掌握運算、借助圖形探索性質、借助線形圖明確關系等，但很多表現為一種“必選動作”，即此教學內容本身就是從幾何直觀而來，如絕對值的概念其本身就源于兩點間的距離，函數的性質其本身就要借助于圖形的探索等等，如果將幾何直觀的體現僅局限于這些“必選動作”，那么幾何直觀的目標定位似乎只是獲得知識的一種圖形工具，獲得知識的橋梁，而不是作為一種思考問題、理解數學的思維方式或能力素養．

借助于圖形描述和分析問題，可以將抽象的問題直觀化，可以將復雜數量關系清晰化，反過來，面對一個抽象的問題或代數表達，能否用恰當的圖形表達自己的理解或用圖形的方法解決問題、整體把握問題，即是幾何直觀思維或能力素養的表現．“幾何直觀首先表現為一種意識一一面對數學問題能想到用畫圖來幫助思考；其次表現為掌握一定的幾何直觀的畫圖技巧，能畫出圖來”[16]，作為教科書應有意識地引導學生進行幾何直觀的思考，將其作為一種能力素養滲透教科書中．

如，平方差公式，除了教科書給出的直觀圖形解釋（圖3），可以進一步提出：你還能給出其它圖形的直觀解釋嗎？

圖3 平方差公式直觀圖形

或在一些問題中采用直觀的方法表達或解決問題，要求學生能夠遷移到新的問題．如在平方差公式之后學習完全平方公式，得到公式后，要求學生自行給出公式的圖形解釋，在其后的因式分解學習中可以再次回顧圖形的解釋．經過這樣的學習積淀，學生看到2、2、自然會想到圖形的面積，因此在因式分解中甚至可以提出挑戰性問題：你能對3-3進行因式分解嗎？你是怎么得到結論的？學生可以借助圖形猜想結論，再通過整式乘法運算驗證結論．

4.2 整體性

從前文分析知，幾何直觀的類型有：直觀表征、直觀分析、直觀解釋和直觀發現，常見的數學活動主要有概念生成、命題探究和問題解決，因此可將幾何直觀分為概念生成過程中的幾何直觀、命題探究過程中的幾何直觀和問題解決過程中的幾何直觀．幾何直觀在不同內容中的分布廣泛程度如表1所示．

對于教科書學習內容，可以更多考慮其直觀表征，盡力溝通數和形的聯系（當然應是自然的），感受數學對象的多角度認識；在命題探究和問題解決過程中，更多考慮直觀分析和直觀解釋，獲得對命題的直觀理解和解釋，學會問題解決的策略；在問題解決過程中，更多考慮直觀發現，獲得對問題的直接領悟，形成一定的數學直觀．

表1 幾何直觀在內容中的分布廣泛度

注：√代表相應表現在此內容中比較廣泛

從當前教科書來看，幾何直觀并不缺乏，但存在內容分布和類型分布偏差情況．從內容來看，在概念形成和命題探究過程中的直觀為多，問題解決過程中的直觀較少，這應該和當前數學課程強調情境、探究有一定的關系，注重概念的形成過程，注重公式、法則等結論的探究，但當獲得結論后用其解決問題幾何直觀相對被忽視了．從類型來看，直觀表征、直觀分析和直觀解釋為多，直觀發現少之又少．相關研究也提供了佐證，一般的數學問題解決過程中，學生并不傾向于使用直觀表征策略[12]．一個有趣的現象是，采用直觀信息加工方式的被試對自己的結論都表示懷疑，并且認為需要進一步的代數驗證[12]，這樣的學習現象首先應該從教科書的編寫角度考慮是否對學生產生了影響．

4.3 漸進性

教科書應通過漸次遞進的設計，促進學生幾何直觀的有序發展．從學生的學習來說，幾何直觀不會自發形成，需要教科書及教學中不斷呈現，需要學生長期的經驗積累，因此應首先關注基本圖形的幾何直觀，幫助學生積淀形成基本圖形的幾何直觀，如一些式的圖形表達，看到(+)會想到長方形的面積，看到|-|會想到數軸上兩點間距離，看到a+b會想到直角三角形的兩個直角邊的平方和，在問題解決中，關注從圖形的角度表征問題的信息，或從圖形的角度思考問題，用線段圖、表格等表達數量關系．通過一些實證研究的結果和教科書編寫團隊的研討，研究者認為，問題表述的類型和圖形的明晰程度是影響學生借助幾何直觀解決問題的外在因素，因此，在幾何直觀的教科書設計時，可以從問題表述的類型和圖形的明晰程度兩個方面進行漸進的設計．

問題表述的類型一般有正向表述的問題、逆向表述的問題和轉換的問題，正向表述的問題指給定代數表達要求給出實際背景或圖形直觀，如給定方程代數表達模型要求賦予實際背景的問題；逆向表述的問題指給定圖形直觀要求給出代數表達，如案例6（1），給出方程信息的圖形表達，要求編寫相應的方程問題；轉換問題則指借助、、之間的關系，由給定和的圖形直觀，給出和或和的圖形直觀，如案例6（2）要求從速度和時間的圖象，判斷它們之間的變化規律，進而推斷路程和時間的變化規律，再反映到直觀圖象中去．審視當前教科書，相對而言，多為正向表述的問題，逆向表述和轉換的問題較少，因此教科書編寫中，在正向表述問題之后，應結合具體內容和學生的學力水平考慮適當增補逆向表述的問題和轉換的問題．

案例6：

（1）請你根據下面的線段圖編一個方程問題，列方程并求解．

（2）下圖給出一輛汽車行駛速度隨時間改變的圖象，請你畫出這輛汽車行駛路程隨時間改變的圖象．

圖形的明晰程度也直接影響著學生借助幾何直觀解決問題的表現，根據圖形的明晰程度可以將圖形的呈現方式分為3類：呈現完整圖形、呈現部分圖形和不呈現圖形．顯然，對于同一問題這3種呈現方式導致問題解決的難度是逐步提升的，因此教科書同樣要考慮其漸進性，從呈現完整圖形到呈現部分圖形再到不呈現圖形，從“示范—引導—自主”引領學生進行幾何直觀的思考，如在列方程解應用問題中，第一階段可以采用分析題意的方式，呈現用線段圖或表格表達問題中的信息，第二階段可以采用要求學生填空的方式呈現線段圖或表格，第三階段則直接要求學生能否用圖形直觀表達問題中的數學信息．

4.4 反思性

弗賴登塔爾指出，反思是重要的數學活動，它是數學活動的核心和動力[17]．新的數學觀念形成后，學習者就會試圖用新的觀念去重新認識已經積累起來的知識、技巧、方法和規律，把它們納入剛剛建立起來的認知結構，這是一個反思過程．數學教學必不可少的一部分就是加強學生的反思，因為數學并不是單純的知識，而是思想、觀念，它既是反思的材料，又是反思的結果．反思能力和其他能力一樣，也不是自然形成的，需要教師有意識地培養．

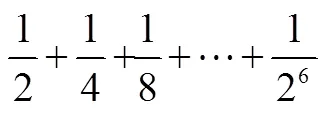
教科書中同樣應設計豐富的反思性活動，引導學生反思借助幾何直觀解決問題的過程，反思幾何直觀的意義與價值等，這方面，現行初中數學教科書尚有較大的提升空間．美國McGraw-Hill出版社出版的初中數學教材Glencoe Math其中有不少好的呈現，如案例7[19]，在函數有關內容章后小結中直接提出這樣的反思性問題：為什么圖表是有用的？請列出圖表有用的3種方式，并分別舉例說明．

幾何直觀是數學中生動的、不斷增長的而且迷人的課題，在內容上、意義上和方法上遠遠超出對幾何圖形本身的研究意義[3]．對教科書幾何直觀的研究必定是其中之一，需要理論的思考，同時需要實踐的檢驗．研究僅對初中數學教科書中幾何直觀的類型和設計原則進行了探討，教科書設計中還有很多問題值得思考和研究：什么內容需要幾何直觀？幾何直觀怎樣呈現？作為教科書怎樣體現在不同學習階段的層次要求等．

案例7：

[1] 史寧中，王尚志．普通高中數學課程標準（2017年版）解讀[M]．北京：高等教育出版社，2018：114．

[2] 中華人民共和國教育部．義務教育數學課程標準（2011年版）[M]．北京：北京師范大學出版社，2012：6．

[3] 秦德生，孔凡哲．關于幾何直觀的思考[J]．中學數學教學參考，2005（10）：9-11．

[4] 黃翔．數學課程標準中的十個核心概念[J]．數學教育學報，2012，21（4）：18．

[5] 孔凡哲，史寧中．關于幾何直觀的含義與表現形式[J]．課程·教材·教法，2012，32（7）：92-97．

[6] 章飛，凌曉牧．幾何直觀的內涵、功能與培養途徑[J]．中學數學教學參考，2013（9）（中旬）：18-20．

[7] 蔣文蔚．幾何直觀思維在科學研究及數學教學中的作用[J]．數學教育學報，1997，6（4）：67．

[8] 徐利治．談談我的一些數學治學經驗[J]．數學通報，2000，39（5）：1．

[9] 蔡宏圣．幾何直觀：小學數學教學的視角[J]．課程·教材·教法，2013，33（5）：109-115．

[10] 馬復．義務教育數學課程標準教科書七上[M]．北京：北京師范大學出版社，2013：150．

[11] 夏光杰．“畫”里有“話”——以畫線段圖解決問題為例談“幾何直觀”[J]．小學教學研究，2016（3）：31-33．

[12] 傅贏芳．數學直觀的認知分析及對教學的啟示[D]．南京：南京師范大學，2009：38，37，62．

[13] 馬復．義務教育數學課程標準教科書七下[M]．北京：北京師范大學出版社，2013：23．

[14] 王鵬遠．談計算機和幾何教學的現代化[J]．中學數學教學參考，1998（7）：23．

[15] 張奠宙，張廣祥．中學代數研究[M]．北京：高等教育出版社，2006：II-III．

[16] 蔡圣宏．幾何直觀的內涵及教育教學價值[J]．廣西教育，2013（10）：36．

[17] 弗賴登塔爾．數學教育再探[M]．劉意竹，楊剛，譯．上海：上海教育出版社，1999：50．

[18] 史寧中．幾何直觀與小學數學教學[R]．金華：第十六屆全國新世紀小學數學課程與教學系列研討會，2017．

[19] ?Carter J, Cuevas G, DayR, et al. Glencoe math course 3 [M]. Columbus: McGraw-Hill Education, 2013: 258.

The Design of “Geometric Intuition” in Junior High School Mathematics Textbooks: Types and Principles

GU Ji-ling1, ZHANG Fei2

(1. College of Teacher Education, Nanjing Normal University, Jiangsu Nanjing 210097, China;2. Institute of Curriculum and Teaching, Jiangsu Second Normal University, Jiangsu Nanjing 210013, China)

Geometric intuition has the educational value of both epistemology and methodology. The types of geometric intuition in junior high school mathematics textbooks are as follows: intuitive representation, intuitive analysis, intuitive interpretation, and intuitive discovery. The geometric intuition design of junior high school mathematics textbooks should follow the principles of: accuracy, both knowledge tools and ability literacy; integrity, considering both content and type to avoid deviation; gradualness, with the type of problem representation and the clarity of the graphics being hierarchical; and reflective, whereby there must be reflective questions and activities.

junior high school mathematics; textbooks; geometric intuition; type; principle

G632.3

A

1004–9894（2021）06–0059–05

顧繼玲，章飛．初中數學教科書中“幾何直觀”的設計類型及原則[J]．數學教育學報，2021，30（6）：59-63．

2021–08–11

江蘇省教育科學“十三五”規劃課題——基于“三段式”研課的全日制數學專碩PCK發展研究（B-b/2018/01/47）

顧繼玲（1971—），女，江蘇建湖人，教授，博士，碩士生導師，主要從事課程與教學論、教師教育研究．章飛為本文通訊作者．

[責任編校：陳雋、陳漢君]