基于ARIMA時間序列模型預測某三級甲等醫院耐碳青霉烯類銅綠假單胞菌的感染率

高勝春 吳紅梅

溫州市人民醫院感染管理科，325000浙江 溫州

近年來，隨著人口老年化及碳青霉烯類抗生素的過度使用，耐碳青霉烯類銅綠假單胞菌（carbapenemresistant pseudomonas aeruginosa，CRPA）菌株逐漸增多，已對臨床控制醫院獲得性感染構成了嚴重威脅［1］。耐藥性監測數據顯示，我國2005—2014年對亞胺培南和美羅培南總的耐藥率分別為31.8% 和28.6%，遠高于歐美等國家［2-3］。監測的目的之一是預測，而現有的關于CRPA的研究大多集中于描述性研究。因CRPA數據存在較大的波動性，無法憑經驗判斷下一周期的數據，容易出現耐藥菌傳播或抗生素過度使用的情況。因此，運用數學模型對CRPA數據進行分析，預測其流行動態，對更好地掌握該耐藥菌流行趨勢具有重要意義。在傳染病的短期預測中，常采用自回歸移動平均模型（autoregressive integrated moving average model，ARIMA），它具有對復雜因素適應性強、模型結構簡單、操作方便、經濟實用等優點［4-5］。ARIMA既適用于平穩時間序列，也適用于非平穩時間序列。因此，它被廣泛應用于季節性和周期性感染的預測。

本研究利用2016年1月至2019年12月浙江省某三級甲等醫院CRPA感染率的監測數據建立ARI-MA時間序列模型，并利用模型對2020年1月至2020年9月的數據進行驗證，為CRPA的管理和預警提供線索和科學依據。

1 資料與方法

1.1 資料來源與ARIMA乘積季節模型的建立

利用該院2016年1月至2019年12月的CRPA感染數據建立ARIMA時間序列模型，后利用模型對2020年1月至2020年9月的數據進行預測，以確定模型的平穩性和可用性。ARIMA時間序列模型基本結構為ARIMA（p，d，q）×（P，D，Q）s。其中，p為自回歸階項；q為移動平均項；d和D分別為提取原序列確定性信息和季節性的差分次數；P和Q則分別代表季節性自回歸和季節性移動平均項；s為季節周期和循環長度。建立ARIMA模型包括4個主要步驟：

（1）序列平穩化。利用原始序列圖和變換后的序列圖來評價序列圖的平穩性和趨勢性。隨后，通過差分或對數變換使有趨勢性的非平穩序列ARIMA模型平穩可逆。

（2）模型識別和定階。通過繪制平穩后自相關函數（ACF）和偏自相關函數（PACF），識別和分析時間序列的隨機性、平穩性和季節性特征。根據BIC一般從0到2確定模型的階數，階數很少超過2，通過0、1和2的不同組合識別出幾個粗略模型，最終選出BIC最小的最優模型。

（3）參數估計與診斷檢驗。用Box－Ljung檢驗識別殘差序列的白噪聲。即在殘差相關檢驗中，殘差必須是隨機的（P＞0.05）。

（4）模型預測。采用最優ARIMA模型對2016年1月至2019年12月的CRPA感染數據進行回代模擬，再利用模型對2020年1月至2020年9月的數據進行預測，并通過計算平均相對誤差來評價ARIMA模型的精度。

1.2 統計學方法

采用SPSS 25.0軟件進行時間序列分析，定義時間變量。首先，將序列圖與相關圖和偏相關分析圖相結合，判斷其是否為平穩序列。如果不是平穩序列，則通過差分、季節差等方法將其轉換為平穩序列，初步確定模型的取值范圍。觀察序列是否穩定的方法是觀察序列圖的均值是否發生顯著變化。通過初步確定模型范圍來進行模型預測，并使用Box-Ljung檢驗來確定其是否是白噪聲序列，若Box-Ljung檢驗P＞0.05，則定為白噪聲序列。如果多個模型通過Box-Ljung檢驗，則使用BIC來確定最優模型。

2 結果

2.1 CRPA感染情況及趨勢分析

2016年1月至2019年12月共發生CRPA感染121例，感染率0.013% ～0.163%。依據CRPA感染率監測數據繪制時間序列圖顯示，CRPA感染全年每月均有發生，感染率波動較大并有一定的周期波動，不滿足序列平穩性的要求。見圖1。

圖1 CRPA感染率原始數據時序圖

2.2 模型識別與定階

由于原序列呈現出周期性季節波動的非平穩序列特點，因此需要建立混合效應模型（p，d，q）×（P，D，Q）s。一階差分后的CRPA感染率的時序圖見圖2，ACF和PACF 圖見圖3。 模型形式為ARIMA（p，1，q）×（P，1，Q）12。利用SPSS的專家建模器從低階到高階逐個對p、q、P和Q的取值進行嘗試，模型擬合的精度通過MAPE和BIC進行比較，取BIC值最小的為最佳模型。結果在建立的8個模型中有3個模型的參數通過統計學檢驗，比較各模型參數，最終確定最優模型為ARIMA（0，1，1）×（0，1，1）12。模型擬合正態化的BIC為3.461，決定系數R2為0.426，根據貝葉斯準則BIC值最小，R2最大為最優模型；Ljung-BoxQ檢驗顯示差異無統計學意義（Q＝16.02，P＝0.38），屬白噪聲序列，提示本模型相對適合。

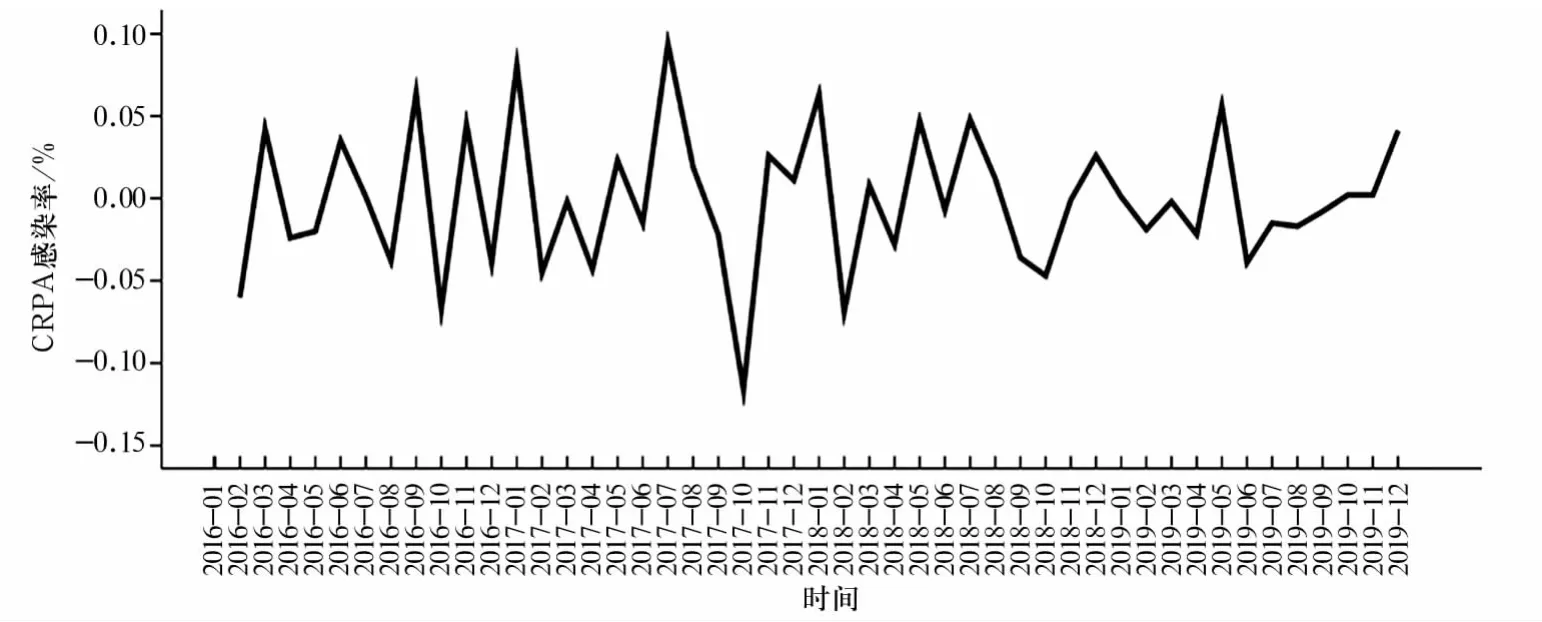
圖2 CRPA感染率一階差分后時序圖

圖3 CRPA感染率一階差分后ACF圖和PACF圖

2.3 模型預測

2020年1月至2020年9月，CRPA感染率實際值與預測值大致相符。見圖4。預測值與實際值的動態趨勢基本一致，平均相對誤差為8.45%。見表1。

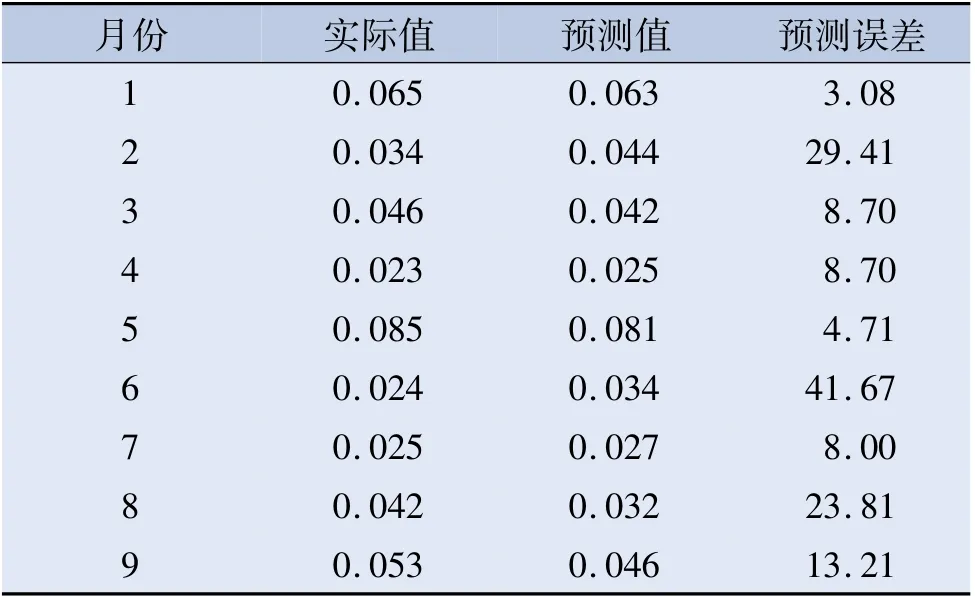
表1 2020年1—9月CRPA感染率驗證結果單位：%

圖4 2016年1月至2020年9月CRPA感染率實際值與預測值的時間序列

3 討論

目前耐碳青霉烯類銅綠假單胞菌具有多種耐藥形式，呈現出從單一耐藥到多藥耐藥，從低耐藥到高耐藥的趨勢，這給臨床治療銅綠假單胞菌感染帶來了巨大的壓力。時間序列預測方法是對時間序列進行匯編和分析，根據時間序列對發展過程、方向和趨勢的反映，通過類比或延伸的方法來預測未來一段時間或幾年內可能達到的水平。其中，ARIMA模型能夠綜合序列的平穩性、季節性和隨機性，不斷修正模型，直到選定最優模型進行疾病研究，已成為應用最廣泛的時間序列預測模型之一。本研究基于ARIMA乘積季節模型預測耐碳青霉烯類銅綠假單胞菌流行趨勢為多重耐藥菌控制策略的制定提供依據，旨在減少CRPA感染的發生。

本研究對浙江省某三級甲等綜合醫院CRPA感染資料進行了分析。通過ARIMA模型，根據BIC標準選擇最優模型。結果表明，ARIMA（0，1，1）×（0，1，1）12模型是CRPA感染率發生的最佳模型。預測值與實測值吻合較好，平均相對誤差為8.45%。各種時間序列模型或方法已被用于預測每月多重耐藥菌的感染率。在移動平均、人工神經網絡、線性回歸和Holt－Winters模型等其他預測方法中［6-8］，ARIMA模型也被證明是比較適合預測多重耐藥菌感染率的模型。一般來說，多重耐藥菌感染并不像瘧疾、白喉、水痘、輪狀病毒、霍亂等疾病那樣表現出明顯的季節性［9-10］，然而一些研究已經使用季節性ARIMA模型研究了多重耐藥菌的季節性影響。儲文杰等［11］基于ARIMA乘積季節模型預測產超廣譜β-內酰胺酶大腸埃希菌流行趨勢，結果表明產超廣譜β-內酰胺酶大腸埃希菌檢出高峰出現在夏秋季節。劉燕等［12］利用ARIMA模型對2016年1—12月多重耐藥鮑曼不動桿菌醫院感染檢出率流行趨勢進行了預測，平均相對誤差為8.45% 。

盡管本研究構建的ARIMA乘積季節模型預測結果較為理想，但與CRPA實際感染率相比仍存在偏差。原因在于本研究建模過程中僅考慮了時間因素，人口統計學和共病變量，如年齡、性別、社會經濟地位和糖尿病，以及與多重耐藥菌傳播相關因素都沒有被考慮在這項回顧性研究中。因此，必須謹慎地解釋預測結果。此外，這項研究是基于浙江省某1家三級甲等醫院數據進行的，因此，結果可能不適用于其他類型醫院。然而，細菌耐藥性是一個復雜的、持續進化的問題，經常是難以預料的。盡管研究者們在努力找尋解決細菌耐藥性的方法，但一些非常簡單的辦法如減少抗生素的使用和開發高效的新藥物在實際應用時卻又非常艱難，因此，這項研究的結果有助于預測CRPA感染率的變化趨勢，幫助醫護人員及時采取感染防控措施，合理分配和使用衛生資源。