凍融RC梁抗震性能與數值模擬方法

鄭山鎖 楊路 姬金銘 裴培 黃瑜 王斌

摘要： 為分析凍融環境下鋼筋混凝土（RC）梁在地震荷載作用下的響應，采用人工環境模擬方法對4件RC梁試件進行了快速凍融試驗，進而對其進行擬靜力加載試驗。結果表明，隨著凍融次數的增加，梁試件滯回曲線的捏縮現象越發明顯，構件延性和耗能能力下降。同時，通過理論推導建立了可考慮凍融損傷的粘結滑移模型，采用有限元分析軟件OpenSEES中的零長度截面單元，并基于可考慮凍融損傷分布的纖維截面模型，對RC梁試件的地震破壞過程進行了數值模擬。分析與試驗結果對比表明，采用數值建模與分析方法得到的滯回曲線與試驗數據基本相符，骨架曲線諸特征值誤差較小，且較好地反映了凍融損傷引起RC梁滯回曲線的捏縮效應，從而驗證了所提出的模擬方法的準確性。

關鍵詞： RC梁; 抗震性能; 凍融循環; 粘結?滑移; 滯回曲線

中圖分類號： TU352.11; TU375.4 文獻標志碼： A 文章編號： 1004-4523（2021）05-0889-10

DOI：10.16385/j.cnki.issn.1004-4523.2021.05.002

引 言

中國地域遼闊，其中東北、華北和西北大部分地區屬于嚴寒或寒冷地區，這些地區的鋼筋混凝土（RC）易遭受凍融循環作用，導致鋼筋混凝土材料性能及粘結性能發生退化，從而造成RC結構的受力性能和抗震性能的劣化[1?2]。嚴寒地區的凍融循環作用已成為影響RC結構耐久性問題的一個重要因素，引起了國內外學者的廣泛關注。施士升[3]、Hanjari[4]等通過試驗分析，揭示了混凝土抗壓強度、抗拉強度、彈性模量等性能指標隨凍融循環次數變化的退化規律。文獻[5]進一步指出混凝土材料耐久性能的逐步退化將會導致RC構件與結構力學性能和抗震性能不斷劣化。在這一背景下，Xu等[6]、鄭捷等[7]、鄭山鎖等[8]通過擬靜力加載試驗，分別探討了RC框架柱、框架節點及剪力墻試件在不同凍融次數下的抗震性能退化規律;張藝欣等[9]則考慮混凝土凍融損傷在構件內部分布的不均勻性，提出了凍融RC柱的數值模擬方法，并據此對不同凍融循環次數下RC柱的抗震性能展開了研究。然而，該數值模擬方法中并未考慮凍融損傷條件下鋼筋與混凝土間的粘結性能劣化。Hadadd等[10]和Fagerlund等[11]通過試驗研究發現，凍融循環作用會導致鋼筋與混凝土間的粘結強度退化，并引起自由端的滑移變形不斷增大。Ma等[12]，Saatcioglu等[13]和Moehle等[14]通過試驗研究發現，由鋼筋滑移產生的固端轉角所引起的變形在RC構件整體變形中可達到50%。因此，為較好地反映凍融RC結構的力學性能和變形能力，Hanjari等[15]基于歐洲規范[16]中粘結滑移模型，提出了考慮凍融影響的粘結滑移模型;然而，該模型僅考慮凍融對粘結強度的影響，忽略了滑移量的變化，且沒有考慮凍融破壞范圍的延伸和分布情況，即缺乏對凍融不均勻性的考慮[17]。

鑒于此，本文首先對4件不同凍融次數下的RC梁試件進行了擬靜力試驗，系統地研究了不同凍融次數對其抗震性能的影響規律;進而通過理論推導，并結合已有研究成果，建立了考慮凍融損傷影響的鋼筋與混凝土材料界面粘結滑移本構模型。據此，采用纖維模型并考慮凍融損傷在構件內部分布的不均勻性以及粘結滑移影響，對上述4件RC梁進行了數值建模分析，通過與試驗結果對比分析，驗證了所建立的粘結滑移本構模型和數值建模方法的準確性與可行性。該成果將為凍融大氣環境下在役RC結構的抗震性能研究奠定基礎。

1 試驗概況

1.1 試件設計與制作

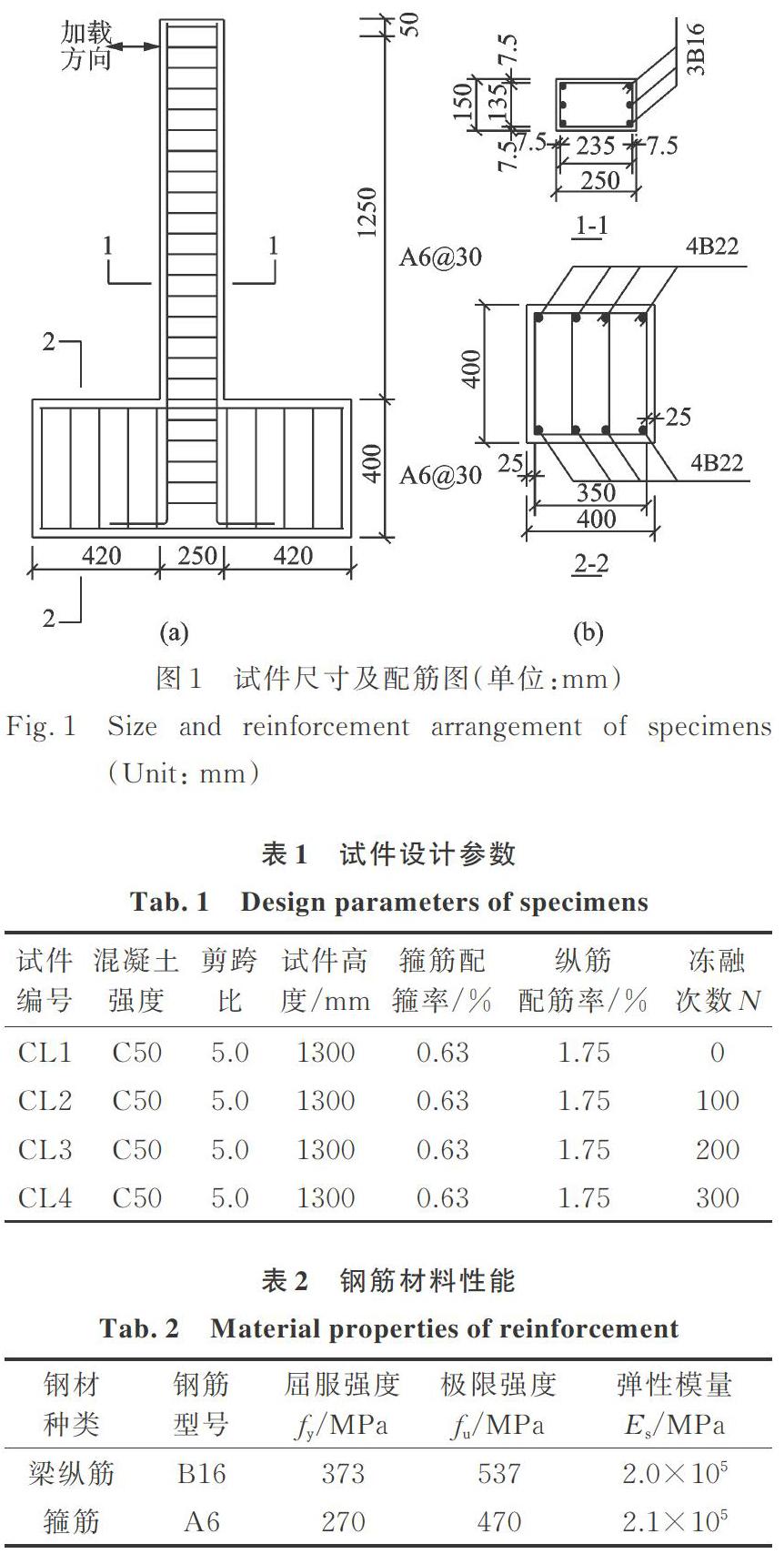
地震作用下，RC框架梁端部易發生損傷破壞，且其跨中存在反彎點，故本文取梁端至反彎點間梁端為研究對象，按照1∶2的縮尺比例設計了4件相同設計參數、不同凍融循環次數的RC梁試件（剪跨比），試件設計參數如表1所示，試件尺寸及配筋圖如圖1所示。鋼筋材料力學性能實測數據及混凝土配合比如表2與表3所示;在梁試件制作的同期，澆筑邊長150 mm的標準立方體試塊，用于測量凍融前后混凝土立方體抗壓強度。

1.2 凍融循環方案

中國規范[18]中的“氣凍水融”條件的慢凍法與“水凍水融”條件的快凍法僅適用于小尺寸混凝土試件，且其試驗條件對于RC梁來說很少在自然環境中真實存在。本試驗參考規范[18]中的慢凍法實施過程，采用人工氣候環境模擬實驗技術，通過控制實驗室中空氣的溫度來實現凍融循環過程中的溫度變化，模擬“氣凍氣融”的自然凍融環境。為獲得良好的凍融效果，試件凍融前需充分浸泡且凍融過程中需間斷噴淋，使試件處于飽和水狀態。每個凍融循環總時長5.5 h，用于降溫及冷凍的時間為4 h，用于升溫、融化及噴淋的時間為1.5 h。本次試驗凍融循環方案如圖2所示。

1.3 凍融后混凝土材料性能

凍融試驗后，測量4組（每組3個）RC梁伴隨立方體試塊抗壓強度，結果如表4所示。可以發現，隨著凍融次數增加，混凝土抗壓強度不斷降低，在經過300次凍融循環后，混凝土強度下降幅度超過30%。試驗結果表明了凍融損傷對混凝土性能的不利影響。

1.4 擬靜力加載方案與制度

為準確模擬RC框架梁在地震作用下的實際受力狀況，采用“懸臂梁”式及位移控制加載方式對各梁試件進行擬靜力加載，具體方案如下：試件屈服前，位移增量為理論計算屈服位移Δy[19]的0.2倍，每級控制位移循環1次;試件屈服后，位移增量為Δy，每級控制位移循環3次;當承載力降至峰值荷載Pc的85%后或破壞明顯時停止試驗加載。加載系統及加載制度如圖3和圖4所示。

1.5 擬靜力試驗結果

試驗加載結束時，梁試件在往復荷載作用下均發生彎曲破壞，各試件破壞過程相似。以未凍融試件CL1為例：隨著試驗加載的進行，當梁頂部水平位移達到1.4 mm時，距梁底部約200 mm高處開始出現初始水平裂縫，標志梁進入了開裂階段，此后加載繼續進行，裂縫不斷延伸并加寬，并伴有新的水平裂縫出現;當位移達到2.7 mm時，梁的角端部位出現開裂現象，且距梁底約250，300，350 mm處陸續出現了水平裂縫，繼續加載，梁底縱向受拉鋼筋逐步屈服，距梁底約350 mm高處的水平裂縫斜向發展為斜裂縫;隨著加載的進行，部分斜裂縫延伸至梁底角部，角部水平裂縫逐步貫穿，裂縫寬度明顯增加，角部混凝土受到嚴重擠壓;水平位移超過32 mm后，梁底部形成兩條明顯的主推與主拉水平裂縫;水平位移超過65 mm后，梁底角部大部分混凝土破碎脫落，鋼筋外露，試件承載力迅速下降，試件宣告破壞。試件加載過程中裂縫分布圖如圖5所示。

隨凍融次數的增多，梁底部水平裂縫出現提前，試件表面裂縫數量增加，梁頂水平荷載到達峰值后下降速率加快，塑性鉸區斜裂縫發展相對迅速，破壞時試件角部混凝土提前被壓碎，呈現顆粒狀，而不是塊狀，破壞更為嚴重。由于凍融后混凝土強度降低，縱筋提前屈服，梁受壓區混凝土酥碎更為嚴重，鋼筋與混凝土的粘結性能弱化導致使鋼筋中應力通過粘結應力傳遞給混凝土時所需傳力長度增長，裂縫間距增大，試件延性隨著凍融次數的增多逐步降低。各試件的破壞狀態圖如圖6所示。

分析各梁試件的滯回曲線（如圖7所示）可知：滯回環的捏縮現象隨凍融次數增多越發明顯，所包圍的面積逐漸減小，表明凍融循環加劇了鋼筋與混凝土間的粘結性能退化，降低了梁的耗能能力。根據滯回曲線，得到如圖8所示不同凍融次數下梁骨架曲線，表5特征點參數由正負向平均骨架曲線標定，其中屈服點由“能量法”[20]而定，極限點取為荷載降至0.85Pc的對應點，累積耗能按計算確定（其中，Ei為第i次循環加載正反循環一周時構件耗散能量，N為循環加載次數）。

從圖8和表5可以看出，梁試件的屈服位移Δy和峰值位移Δc均隨凍融循環次數增多而逐漸增大，極限位移Δu逐漸減小，從而延性系數（）不斷降低;屈服荷載Py、峰值荷載Pc和極限荷載Pu均隨凍融循環次數的增多而呈降低趨勢，但相比于表4凍融后混凝土抗壓強度降低程度而言該降低趨勢并不顯著，其原因為：凍融損傷是從混凝土表層向其內部發展的，梁試件尺寸相對較大，僅表層出現凍融損傷，而材性試驗中混凝土試塊尺寸較小，故其凍融損傷相對嚴重。

2 考慮凍融損傷的粘結滑移本構模型

既有研究結果顯示[10]，凍融作用會致使鋼筋和混凝土間粘結強度下降，滑移變形增大，因此，為準確反映凍融損傷RC梁的力學性能與抗震性能，有必要在建立粘結滑移本構模型時考慮凍融損傷影響。凍融后鋼筋混凝土間粘結性能劣化主要是由混凝土力學性能退化所引起，因此，本文首先介紹未凍融損傷鋼筋與混凝土間的粘結滑移本構模型，繼而考慮凍融循環作用對混凝土力學性能的影響，對該模型進行修正，建立考慮凍融損傷的粘結滑移本構模型。

2.1 粘結滑移本構模型

鋼筋與混凝土間的粘結應力分布不僅受混凝土強度、鋼筋直徑、保護層厚度、橫向約束等多種因素影響，還涉及位置函數等復雜變量[21]。Yu等[22]指出，在結構分析中如果直接應用粘結應力與滑移量s表示的粘結滑移關系將會增加數值建模的復雜性;因此，基于鋼筋應力與粘結應力良好的相關性，本文在數值模擬中采用鋼筋應力與滑移量s表示的粘結滑移本構關系，以避免分析過程中復雜的微分迭代計算及位置函數的引入，簡化計算過程。Zhao等[23]提出將零長度纖維單元與普通纖維單元串聯的思路，并在零長度截面中采用鋼筋應力?滑移本構關系替代傳統鋼筋應力?應變關系，以模擬懸臂構件的彎曲變形和滑移變形，并進行了廣泛應用[24?27]。本文基于此研究思路，首先通過鋼筋應力?粘結應力?鋼筋應變?滑移量間相關關系推導得出鋼筋應力?滑移本構關系，進而將該本構關系賦予零長度單元中的鋼筋，以模擬梁端滑移量，最終得到考慮粘結滑移效應的梁端轉角或梁頂側向位移。

Altoontash[28]在模型分析中采用表示的粘結滑移關系，并提出如下假設：1）根據能量耗散等效原理，分別將鋼筋應力小于和大于fy長度上的粘結應力假定為均勻分布的平均粘結應力和（如圖9所示）;2）滑移是鋼筋與混凝土間相對變形的結果;3）鋼筋應力為0時相應的滑移量也為0。此外，Otani等[29]也曾將鋼筋與混凝土間的粘結應力分布假定為沿鋼筋應力發展長度上的均勻分布，Sezen等[30]則在Otani的基礎之上提出了階梯狀均勻分布的粘結應力分布模式，并將其應用于分析模型中，取得了良好的模擬效果。

基于上述分析，本文依據鋼筋是否達到屈服強度，將鋼筋與混凝土間的粘結應力分布劃分為如圖10所示兩種情況，并據此建立由關系表示的粘結滑移本構模型。其中鋼筋應變根據雙線型本構關系定義如下

式中 為鋼筋應力，為鋼筋屈服強度;為鋼筋彈性模量;為鋼筋硬化模量，取為的2.5%。

根據圖10，建立鋼筋與混凝土間的粘結滑移關系如下：

（1）鋼筋屈服前，其與混凝土間的粘結應力沿鋼筋應力發展長度ls呈均勻的分布（如圖10（a）所示），則由力學平衡關系可得

式中 為鋼筋應力，;d和As分別為鋼筋直徑和橫截面面積;為鋼筋應力發展長度上均勻分布的平均粘結應力，參考Lowes等[31]的研究結果，其值取為1.4，為混凝土抗壓強度。

鋼筋錨固滑移量s為鋼筋應力發展長度上鋼筋的累積變形，其值按下式計算：

式中 和分別為錨固鋼筋應力小于和大于fy區段的長度;為沿分布的平均粘結應力，根據文獻[31]取為0.4。

當鋼筋應力達到極限強度時，鋼筋應變滲透引起的滑移達到極限滑移值su。則由式（5）可得

基于以上分析，建立未凍融損傷下鋼筋與混凝土間以鋼筋應力與滑移量s表示的粘結滑移本構關系，如下式所示

具體模型見圖11中0次凍融曲線。

2.2 修正的粘結滑移本構模型

Fagerlund等[11]通過試驗研究發現，凍融損傷將導致鋼筋與混凝土間的粘結強度不斷降低，且下降幅度在30%?70%之間;Hanjari等[32]的研究結果表明，凍融損傷混凝土抗壓強度降低25%?50%時，其與鋼筋間的粘結強度退化約15%?50%;Petersen等[17]則發現，當凍融損傷程度較輕時，試件破壞僅限于混凝土保護層的開裂剝落，且在最大粘結強度下可以觀察到微小的滑移增長量;當凍融損傷深入試件內部，即凍融損傷程度較重時，鋼筋與混凝土粘結強度驟降，滑移量顯著增大，且隨凍融損傷程度的加劇，鋼筋混凝土間粘結性能退化愈加嚴重。上述研究結果均表明，凍融損傷對鋼筋與混凝土間粘結性能的影響不容忽視。因此在建立鋼筋與混凝土粘結滑移本構模型時有必要考慮凍融損傷的影響。

凍融損傷后，鋼筋混凝土粘結性能劣化的主要原因在于混凝土力學性能的退化，因此，本文通過考慮凍融循環作用對混凝土力學性能的影響，對2.1中給出的粘結滑移本構模型進行修正，以建立考慮凍融損傷影響的粘結滑移本構模型。具體方法如下：

（1）凍融混凝土抗壓強度

張藝欣等[9]以相對動彈性模量（RDME）為參數，建立了凍融混凝土抗壓強度計算模型，其表征如下

式中 R為凍融損傷后不同深度處混凝土的RDME;N為凍融循環次數;為凍融混凝土動彈性模量開始發生退化時的臨界凍融循環次數;xi為試件內部混凝土到試件受凍邊緣的最小距離。

然而，需要指出的是：上述公式中的N為Petersen凍融試驗方法中的凍融循環次數[17]，本試驗中各試件的凍融方法與Petersen的不同，因而同樣凍融次數下混凝土的凍損程度并不一致，從而公式（10）無法直接應用于本研究中。文獻[9]以RDME退化程度相同作為等效原則，建立了其試驗條件下的凍融循環次數NE與Petersen試驗條件下凍融循環次數NP的對應關系（如表6所示），本試驗中各試件的凍融試驗條件與文獻[9]的相同。因此，可采用表6中的對應關系，將本試驗的凍融循環次數變換為Petersen試驗的凍融循環次數。

（2）考慮凍融影響的鋼筋混凝土粘結滑移本構模型

基于鋼筋與混凝土間粘結強度與混凝土抗壓強度間的關系，將修正后的混凝土抗壓強度公式（10）代入式（9），即可得考慮凍融損傷影響的鋼筋混凝土粘結滑移本構關系

式中 為凍融混凝土抗壓強度，根據式（10）計算確定。據此，得到不同凍融循環次數下以鋼筋應力與滑移量s表示的粘結滑移本構關系，如圖11所示。可以看出，隨凍融循環次數增多：鋼筋屈服前，鋼筋與混凝土間的滑移變形緩慢增長;而當鋼筋屈服后，在較大的應變滲透作用影響下，滑移變形顯著增大。

3 有限元建模及模型驗證

為驗證所建立的考慮凍融影響的鋼筋混凝土粘結滑移本構模型的準確性，基于OpenSees有限元分析平臺，采用纖維模型并考慮凍融損傷的不均勻性及錨固粘結滑移影響，建立凍融損傷RC梁試件的數值模型。

3.1 數值建模

文獻[9]將其提出的凍融混凝土“不均勻損傷”模型及RC柱擬靜力試驗結果與段安[33]提出的凍融混凝土“全截面損傷”模型進行對比，分析不同凍融次數、軸壓比及混凝土強度因素下試驗與模擬結果的滯回曲線，結果表明不均勻損傷模型更接近于試驗結果，可以良好地模擬凍融損傷后的RC柱構件地震反應。然而，該模型中并未考慮凍融損傷條件下鋼筋與混凝土間的粘結性能劣化。

本文參考文獻[9]，采用纖維模型模擬RC梁的彎曲變形，并考慮不同深度處混凝土凍融損傷的不均勻性，將構件不同深度處混凝土纖維分別賦予不同的凍融損傷混凝土本構關系，具體數值建模方法及凍融損傷混凝土本構模型參數標定方法參見文獻[9]。同時，為考慮凍融后混凝土與鋼筋間粘結性能劣化對RC梁力學與抗震性能的影響，引入零長度截面單元（zeroLengthSection）模擬梁錨固端縱筋的粘結滑移效應，通過串聯非線性梁柱單元與零長度截面單元，形成RC梁整體數值分析模型，如圖12所示。根據構件配筋及等效塑性鉸高度，模型沿梁高劃分6個單元，節點1與節點6之間為非線性纖維梁柱單元，節點1與節點7之間為零長度截面單元。該零長度單元截面中的混凝土本構采用Concrete01模型，并參考文獻[7]，考慮不同深度處混凝土凍融損傷的不均勻性;鋼筋材料本構則采用Pinching4模型，以反映往復加載過程中粘結滑移滯回曲線的捏縮效應以及加、卸載剛度退化和強度衰減現象，Pinching4模型骨架曲線參數根據本文第2節中公式（13）計算確定，滯回規則控制參數則參考文獻[25]確定。

3.2 模型驗證

基于上述建模方法，分別對不同凍融循環次數下的RC梁試件進行數值建模與分析，并將分析結果與試驗的結果進行對比，其中滯回曲線對比如圖13所示。

由圖13可以看出，4件RC梁試件數值分析得到的滯回曲線與試驗滯回曲線均呈現出明顯的捏縮現象，模擬所得各階段剛度及滯回性能與試驗測試結果基本一致，整體吻合較好。同時，對比模擬與試驗所得屈服點和峰值點的特征值（如圖14所示），可以看出其誤差基本不超過15%，表明采用本文建立的數值模型所得各試件骨架曲線與試驗結果符合較好，能夠對凍融RC梁各階段受力性能進行較準確的模擬。分析誤差產生的原因：一方面是由于本文在數值模擬中采用的凍融循環次數是基于文獻[9]試驗回歸分析得到的等效凍融循環次數，這與實際結果之間存在一定的差異;其次，由于所建立模型中未考慮剪切變形的影響，并忽略了凍融引起的試件剪切剛度退化，從而導致模擬滯回曲線的卸載剛度大于試驗值，并高估了結構實際變形能力，致使模擬得到的結構耗能和承載力均略大于試驗結果。

4 結 論

本文采用試驗研究、理論推導及數值建模與分析相結合的方法，研究了凍融RC梁抗震性能劣化規律及其考慮粘結滑移影響的數值建模分析方法，主要成果與結論如下：

（1）隨著凍融次數增多，RC梁滯回曲線的捏縮現象越發明顯，延性和耗能能力均不斷降低，表明凍融循環將導致鋼筋與混凝土間粘結性能劣化。

（2）建立了考慮凍融影響的鋼筋混凝土粘結滑移本構模型，分析與試驗的結果對比表明，所建模型能夠較準確地反映凍融損傷后鋼筋與混凝土間粘結性能的劣化規律。

（3）建立了可考慮凍融損傷不均勻分布、粘結滑移效應和等效凍融循環次數的凍融RC梁纖維截面模型及其數值建模分析方法，對比分析表明，其數值模擬方法可較好地反映凍融RC梁的力學與抗震性能退化規律。

參考文獻：

[1] MEHTA P K. Concrete durability： Fifty years progress[C]. Proceedings of 2nd International Conference on Concrete Durability. Farmington Hills， MI： American Concrete Institute， 1991： 1-33.

[2] 張士萍， 鄧敏， 唐明述. 混凝土凍融循環破壞研究進展[J]. 材料科學與工程學報， 2008，26（6）：990-994.

ZHANG Shiping， DENG Min， TANG Mingshu. Advance in research on damagement of concrete due to freeze-thaw cycles[J]. Journal of Materials Science and Engineering， 2008，26（6）：990-994.

[3] 施士升. 凍融循環對混凝土力學性能的影響[J]. 土木工程學報， 1997，30（4）：35-42.

Shi Shisheng. Effect of freezing-thawing cycles on mechanical properties of concrete[J]. China Civil Engineering Journal， 1997，30（4）：35-42.

[4] Hanjari K Z. Structural behaviour of deteriorated concrete Structures[D]. Gothenburg： Chalmers University of Technology， 2010.

[5] D'Ambrisi A， De Stefano M， Tanganelli M， et al. Influence of the variability of concrete mechanical properties on the seismic response of existing RC framed structures[M]∥Seismic Behaviour and Design of Irregular and Complex Civil Structures. Geotechnical， Geological and Earthquake Engineering， 2013， volume 24. Springer， Dordrecht.

[6] XU Shanhua， LI Anbang， JI Zengyang， et al. Seismic performance of reinforced concrete columns after freeze?thaw cycles[J]. Construction & Building Materials， 2016， 102：861-871.

[7] 鄭 捷， 董立國， 秦 卿，等. 凍融循環下鋼筋混凝土框架梁柱中節點抗震性能試驗研究[J]. 建筑結構學報， 2016， 37（10）：73-81.

Zheng Jie， Dong Liguo， Qin Qing， et al. Experimental study on seismic behaviors of RC beam-column joints after freeze-thaw cycles[J]. Journal of Building Structures， 2016， 37（10）：73-81.

[8] 鄭山鎖， 甘傳磊， 秦 卿， 等. 凍融循環后一字形短肢剪力墻抗震性能試驗研究[J]. 工程力學， 2016， 33（12）：94-103.

Zheng Shansuo， Gan Chuanlei， Qin Qing， et al. Experimental study on the seismic behavior of short-pier shear walls subjected to freeze-thaw cycles [J]. Engineering Mechanics， 2016， 33（12）： 94-103.

[9] 張藝欣， 鄭山鎖， 裴 培， 等. 鋼筋混凝土柱凍融損傷模型[J]. 工程力學， 2019，36（2）：78-86.

Zhang Yixin， Zheng Shansuo， Pei Pei， et al. Research on the modelling method of reinforced concrete column subjected to freeze-thaw damage[J]. Engineering Mechanics， 2019，36（2）：78-86.

[10] Haddad R H， Numayr K S. Effect of alkali-silica reaction and freezing and thawing action on concrete?steel bond[J]. Construction & Building Materials， 2007， 21（2）： 428-435.

[11] Fagerlund G， Janz M， Johannesson B. Effect of frost damage on the bond between reinforcement and concrete[R]. Division of Building Materials， Lund Institute of Technology， Sweden， 1994.

[12] Ma S Y M， Bertero V V， Popov E P. Experimental and analytical studies on hysteretic behaviour of recnforced concrete rectangular and T-beam[R]. University of California， Berkeley， 1976， Rep. No. EERC 76-2.

[13] Saatcioglu M， Ozcebe G. Response of reinforced concrete columns to simulated seismic loading[J]. ACI Structural Journal， 1989， 86（1）： 3-12.

[14] Moehle J P， Lehman D E. Seismic performance of confined concrete bridge columns[C]. International Symposium on Confined Concrete. Changsha， China， 2006， 238： 23-42.

[15] Hanjari Kamyab Z， Kettil Per， Lundgren Karin. Modelling the structural behavior of frost-damaged reinforced concrete structures[J]. Structure & Infrastructure Engineering， 2013， 9（5）： 416-431.

[16] Euro-International Committee for Concrete. CEB-FIP Model Code 1990[S]. London： Thomas Telford， 1993.

[17] Petersen L， Lohaus L， Anna M P. Influence of freezing-and-thawing damage on behavior of reinforced concrete elements[J]. ACI Materials Journal， 2007， 104（4）： 369-378.

[18] GB/T 50082-2009，普通混凝土長期性能和耐久性能試驗方法標準[S]. 北京： 中國建筑工業出版社， 2009.

GB/T 50082-2009， Standard for test methods of long-term performance and durability of ordinary concrete [S]. Beijing： China Building Industry Press， 2009.

[19] Watson S， Park R. Simulated seismic load tests on reinforced concrete columns[J]. Journal of Structural Engineering， 1996， 120（6）： 1825-1849.

[20] Mahin S A ， Bertero V V. Problems in establishing and predicting ductility in aseismic design[C]. Proceedings of the International Symposium on Earthquake Structural Engineering， St. Louis， USA， 1976： 613-628.

[21] Somayaji S， Shah S P. Bond stress versus slip relationship and cracking response of tension members[J]. Journal of the American Concrete Institute， 1981， 78（3）： 217-225.

[22] Yu J， Tan K H. Bar stress-slip relationship in reinforced concrete joints with large inelastic bar strains[C]. International Conference of Design and Analysis of Protective Structures， 2012.

[23] Zhao J， Sritharan S. Modeling of strain penetration effects in fiber-based analysis of reinforced concrete structures[J]. ACI Structural Journal， 2007， 104（2）： 133-141.

[24] 楊 紅， 徐海英， 王志軍. 考慮柱底縱筋滑移的纖維模型及框架地震反應分析[J]. 建筑結構學報， 2009， 30（4）： 130-137.

YANG Hong， XU Haiying， WANG Zhijun. Seismic responses analysis of RC frame based on fiber model considering bar slippage at column bottom section[J]. Journal of Building Structures，2009，34（4）：130-137.

[25] Melo J， Fernandes C， Varum H， et al. Numerical modelling of the cyclic behavior of RC elements built with plain reinforcing bars?[J]. Engineering Structures， 2011， 33（2）： 273-286.

[26] Jeon J， Lowes L N， Desroches R， et al. Fragility curves for non-ductile reinforced concrete frames that exhibit different component response mechanisms[J]. Engineering Structures， 2015， 85： 127-143.

[27] 孫治國， 陳 燦， 司炳君， 等. 考慮非線性剪切效應的RC橋墩抗震分析模型[J]. 工程力學， 2015， 32（5）： 28-36.

SUN Zhi-guo， CHEN Can， SI Bing-jun， et al. Seismic analysis model considering nonlinear shear effect for RC bridge piers[J]. Engineering Mechanics， 2015， 32（5）： 28-36.

[28] Altoontash A. Simulation and damage models for performance assessment of reinforced concrete beam?column joints[D]. Stanford： Stanford University， 2004.

[29] Otani S， Sozen M A. Behavior of multistory reinforced concrete frames during earthquakes[D]. Urbana， IL：University of Illinois， 1972.

[30] Sezen H， Moehle J P. Bond-slip behavior of reinforced concrete members [C]. Fib Symposium （CEB-FIP）， Concrete Structures in Seismic Regions. Athens， Greece， 2003.

[31] Lowes L N， Altoontash A. Modeling reinforced-concrete beam-column joints subjected to cyclic loading [J]. Journal of Structural Engineering， 2003， 129（12）： 1686-1697.

[32] Hanjari K Z， Utgenannt P， Lundgren K. Frost-damaged concrete： Part 2. Bond properties [C]. International Conference on Construction Materials： Performance， Innovations and Structural Implications. 2009： 761-766.

[33] 段 安. 受凍融混凝土本構關系研究和凍融過程數值模擬[D]. 北京： 清華大學， 2009.

Duan An. Research on constitutive relationship of freeze-thawed concrete and mathematical modeling of freeze-thaw process [D]. Beijing： Tsinghua University， 2009.

作者簡介： 鄭山鎖（1960?），男，教授。電話：13991835628; E?mail： zhengshansuo@263.net

通訊作者： 楊 路（1999?），女，碩士研究生。電話：18829045739; E?mail： yl2946584790@163.com