大檔距特高壓覆冰輸電線(xiàn)路起舞風(fēng)速TTMD控制優(yōu)化研究
樓文娟 溫作鵬 梁洪超

摘要: 針對(duì)大檔距特高壓輸電線(xiàn)路舞動(dòng)難以防治的問(wèn)題,設(shè)計(jì)了一種電渦流扭轉(zhuǎn)向調(diào)諧質(zhì)量阻尼器(TTMD),并論證了相比于豎向阻尼器具有更強(qiáng)的適用性。從整檔線(xiàn)路力學(xué)模型出發(fā),推導(dǎo)了整檔線(xiàn)路覆冰導(dǎo)線(xiàn)?TTMD系統(tǒng)的舞動(dòng)偏微分方程,選取全局形函數(shù)離散得到常微分方程,采用李雅普諾夫穩(wěn)定定理計(jì)算起舞風(fēng)速。建立基于遺傳算法的TTMD防舞優(yōu)化設(shè)計(jì)方法,考慮到真實(shí)環(huán)境中導(dǎo)線(xiàn)覆冰偏角存在較大的不確定性,以大范圍多覆冰偏角下導(dǎo)線(xiàn)最小起舞風(fēng)速為優(yōu)化目標(biāo),對(duì)TTMD的頻率比、阻尼比、質(zhì)量比、安裝位置、導(dǎo)線(xiàn)張力、覆冰質(zhì)量等參數(shù)進(jìn)行優(yōu)化設(shè)計(jì)。以某500 m大檔距特高壓輸電線(xiàn)路覆冰八分裂導(dǎo)線(xiàn)為例進(jìn)行優(yōu)化設(shè)計(jì),計(jì)算結(jié)果表明:當(dāng)質(zhì)量比高于0.005時(shí),TTMD即可有效地提高最小起舞風(fēng)速;TTMD的推薦安裝位置范圍為導(dǎo)線(xiàn)左側(cè)1/4跨?右側(cè)1/4跨;TTMD控制效果具有良好的魯棒性;設(shè)計(jì)TTMD時(shí),應(yīng)當(dāng)采用較高的導(dǎo)線(xiàn)張力、較低的覆冰質(zhì)量設(shè)定,以得到偏于安全的TTMD參數(shù)設(shè)計(jì)值。
關(guān)鍵詞: 風(fēng)致振動(dòng); 覆冰多分裂導(dǎo)線(xiàn); 防舞; 特高壓; 扭轉(zhuǎn)向調(diào)諧質(zhì)量阻尼器 (TTMD)
中圖分類(lèi)號(hào): TU312+.1; TM752+.5 文獻(xiàn)標(biāo)志碼: A 文章編號(hào): 1004-4523(2021)05-0934-09
DOI:10.16385/j.cnki.issn.1004-4523.2021.05.006
引 言
為適應(yīng)不斷增長(zhǎng)的電力需求,近年來(lái)中國(guó)有越來(lái)越多的特高壓線(xiàn)路建成使用。覆冰特高壓線(xiàn)路在風(fēng)力作用下舞動(dòng)現(xiàn)象時(shí)有發(fā)生,對(duì)電力安全造成威脅[1]。特高壓線(xiàn)路的桿塔高度提升,導(dǎo)線(xiàn)分裂數(shù)增加,一旦發(fā)生舞動(dòng),其振動(dòng)能量較大,防治難度相比于一般線(xiàn)路更大。對(duì)于大檔距特高壓線(xiàn)路的舞動(dòng)防治,目前已有相間間隔棒、回轉(zhuǎn)式間隔棒、相地間隔棒、雙擺防舞器等,這些措施雖起到一定作用,但均存在一些局限性。因此,研究更為有效的舞動(dòng)控制措施,對(duì)減少特高壓線(xiàn)路破壞,保障電力安全具有重要意義。
現(xiàn)有的舞動(dòng)機(jī)理研究表明,氣動(dòng)負(fù)阻尼是導(dǎo)致輸電線(xiàn)路舞動(dòng)的根本原因[2?5],因此提高導(dǎo)線(xiàn)結(jié)構(gòu)阻尼是一種有效的舞動(dòng)控制方式。調(diào)諧質(zhì)量阻尼器(Tuned Mass Damper,TMD)是一種被廣泛應(yīng)用的阻尼器,其在輸電線(xiàn)路防舞中的應(yīng)用研究已初步開(kāi)展[6?9],研究表明調(diào)諧質(zhì)量阻尼器能夠有效增加起舞風(fēng)速并減小舞動(dòng)幅值。但這些研究?jī)H對(duì)單一覆冰偏角條件下TMD的有效性進(jìn)行了驗(yàn)證,然而多分裂導(dǎo)線(xiàn)的氣動(dòng)力特性非常復(fù)雜,不同覆冰偏角工況下導(dǎo)線(xiàn)舞動(dòng)特性存在較大差異。一種好的防舞策略不僅僅只是針對(duì)某一固定覆冰偏角有效,而是要對(duì)惡劣天氣下可能出現(xiàn)的大范圍多覆冰偏角情況下的舞動(dòng)防治均有效,因此,本文以大范圍多覆冰偏角下導(dǎo)線(xiàn)最小起舞風(fēng)速為優(yōu)化目標(biāo)進(jìn)行防舞優(yōu)化設(shè)計(jì)。
現(xiàn)有研究中的TMD均針對(duì)導(dǎo)線(xiàn)的豎向運(yùn)動(dòng)進(jìn)行控制,但大檔距導(dǎo)線(xiàn)的自振頻率較低,TMD的彈性元件靜態(tài)伸長(zhǎng)量可長(zhǎng)達(dá)數(shù)米,可能引發(fā)碰撞問(wèn)題,因此TMD對(duì)大檔距特高壓線(xiàn)路難以適用。另外,大檔距多分裂導(dǎo)線(xiàn)的豎向頻率與扭轉(zhuǎn)頻率較為接近,其舞動(dòng)往往表現(xiàn)出豎?扭耦合的特點(diǎn),扭轉(zhuǎn)向運(yùn)動(dòng)對(duì)于舞動(dòng)激發(fā)相當(dāng)重要,因此采用扭轉(zhuǎn)向調(diào)諧質(zhì)量阻尼器(Torsional Tuned Mass Damper, TTMD)進(jìn)行防舞在原理上是可行的。TTMD運(yùn)行空間要求小,不存在自重引起的豎向變形,能夠普遍適用于各種檔距的多分裂線(xiàn)路舞動(dòng)的防治,尤其可以應(yīng)用于豎向TMD不再適用的大檔距線(xiàn)路。
三自由度節(jié)段模型是導(dǎo)線(xiàn)舞動(dòng)分析常用的模型[1],但該模型無(wú)法考慮多階耦合,也無(wú)法進(jìn)行阻尼器安裝位置的優(yōu)化。因此,有必要針對(duì)TMD難以適用的大檔距輸電線(xiàn)路,建立加裝TTMD的覆冰導(dǎo)線(xiàn)整檔線(xiàn)路模型,研究大范圍覆冰偏角下TTMD對(duì)大檔距特高壓輸電線(xiàn)路的舞動(dòng)控制效果。
阻尼器的參數(shù)、安裝位置決定了阻尼器對(duì)結(jié)構(gòu)的控制效果,對(duì)這些參數(shù)的優(yōu)化是阻尼器設(shè)計(jì)的關(guān)鍵。遺傳算法是一種借鑒自然選擇、自然遺傳機(jī)制的隨機(jī)搜索算法,具有較高的計(jì)算效率,在土木結(jié)構(gòu)的振動(dòng)控制領(lǐng)域已有廣泛應(yīng)用[10?11]。Hervé等[10]針對(duì)加裝TMD的多層木結(jié)構(gòu)采用遺傳算法對(duì)TMD參數(shù)進(jìn)行優(yōu)化,并檢驗(yàn)了不同地震波下的控制效果。陳鑫等[11]針對(duì)風(fēng)荷載作用下加裝調(diào)諧液體阻尼器的高聳鋼煙囪結(jié)構(gòu),采用遺傳算法展開(kāi)多目標(biāo)優(yōu)化,對(duì)結(jié)構(gòu)響應(yīng)及阻尼器行程取得良好控制效果。
本文針對(duì)大檔距特高壓輸電線(xiàn)路舞動(dòng)防治設(shè)計(jì)了一種電渦流扭轉(zhuǎn)向調(diào)諧質(zhì)量阻尼器,并進(jìn)行優(yōu)化研究。推導(dǎo)整檔覆冰導(dǎo)線(xiàn)?TTMD系統(tǒng)的運(yùn)動(dòng)方程,采用李雅普諾夫穩(wěn)定定理計(jì)算起舞風(fēng)速;建立基于遺傳算法的TTMD防舞優(yōu)化設(shè)計(jì)方法,以大范圍多覆冰偏角下導(dǎo)線(xiàn)最小起舞風(fēng)速為優(yōu)化目標(biāo),對(duì)TTMD各項(xiàng)參數(shù)進(jìn)行優(yōu)化設(shè)計(jì);以某500 m大檔距特高壓輸電線(xiàn)路覆冰八分裂導(dǎo)線(xiàn)為例,研究TTMD控制效果與頻率比、阻尼比、質(zhì)量比、安裝位置、導(dǎo)線(xiàn)張力、覆冰質(zhì)量等參數(shù)的關(guān)系,驗(yàn)證TTMD對(duì)起舞風(fēng)速控制效果的有效性和魯棒性。
1 計(jì)算方法
1.1 TTMD?覆冰導(dǎo)線(xiàn)運(yùn)動(dòng)方程及舞動(dòng)穩(wěn)定判定
本文對(duì)多分裂導(dǎo)線(xiàn)舞動(dòng)計(jì)算作以下假設(shè)[12?13]:(1)各子導(dǎo)線(xiàn)物理參數(shù)一致,不考慮彎曲變形;(2)剛性間隔棒均勻分布,對(duì)于子導(dǎo)線(xiàn)運(yùn)動(dòng)完全約束;(3)風(fēng)荷載滿(mǎn)足準(zhǔn)定常假定;(4)導(dǎo)線(xiàn)沿長(zhǎng)度方向均勻覆冰。
自重作用下導(dǎo)線(xiàn)形狀受導(dǎo)線(xiàn)張力控制,利用下式迭代計(jì)算可得導(dǎo)線(xiàn)覆冰后的新張力[14]
式中 H0和H分別為覆冰前、后的導(dǎo)線(xiàn)張力,E為導(dǎo)線(xiàn)彈性模量,A為導(dǎo)線(xiàn)截面積,Ls為單跨導(dǎo)線(xiàn)檔距,q0和q分別為覆冰前、后的導(dǎo)線(xiàn)豎向均布荷載。
多分裂導(dǎo)線(xiàn)的整體坐標(biāo)系定義如圖1所示,s為沿導(dǎo)線(xiàn)軸向的坐標(biāo)。
導(dǎo)線(xiàn)整體運(yùn)動(dòng)位移可表示為軸向位移u、豎向位移v、水平(面外)位移w和扭轉(zhuǎn)位移θ,導(dǎo)線(xiàn)上第j個(gè)TTMD扭轉(zhuǎn)移為θdj。通過(guò)漢密爾頓原理推導(dǎo)得覆冰導(dǎo)線(xiàn)?TTMD系統(tǒng)運(yùn)動(dòng)的偏微分方程
式中 分別為質(zhì)量矩陣、增量剛度矩陣、阻尼矩陣、增量位移、增量荷載。根據(jù)式(6),采用Newmark?β法進(jìn)行計(jì)算可得導(dǎo)線(xiàn)運(yùn)動(dòng)時(shí)程。
李雅普諾夫第一穩(wěn)定定理[15]證明了可以根據(jù)非線(xiàn)性系統(tǒng)的線(xiàn)性化方程,即一次近似方程的特征值實(shí)部正負(fù),判斷非線(xiàn)性系統(tǒng)的穩(wěn)定性。舞動(dòng)作為典型的氣動(dòng)失穩(wěn)現(xiàn)象,也可以通過(guò)計(jì)算運(yùn)動(dòng)方程的線(xiàn)性化方程特征值從而快速判斷是否發(fā)生舞動(dòng)。若特征值實(shí)部均為負(fù),則表明系統(tǒng)穩(wěn)定;若存在某一特征值實(shí)部為正,則表明系統(tǒng)失穩(wěn)。式(6)的特征值可通過(guò)其Jacobi矩陣進(jìn)行計(jì)算[16]
式中 為零矩陣,其所有元素均為0,為單位對(duì)角矩陣,除對(duì)角元素為1外,其余均為0。與分別為矩陣的特征值與對(duì)應(yīng)特征向量,和分別為系統(tǒng)初始狀態(tài)(即位移和速度都為0)時(shí)的總剛度矩陣和總阻尼矩陣,其值如下
式中 為氣動(dòng)阻尼矩陣,為氣動(dòng)剛度矩陣。
1.2 考慮覆冰偏角范圍的防舞優(yōu)化設(shè)計(jì)遺傳算法
真實(shí)環(huán)境中導(dǎo)線(xiàn)非圓截面偏心覆冰一般形成于線(xiàn)路迎風(fēng)側(cè)。隨著冰風(fēng)氣候條件的變化,導(dǎo)線(xiàn)的覆冰方向會(huì)發(fā)生偏轉(zhuǎn),覆冰偏角存在一定的變化范圍。導(dǎo)線(xiàn)覆冰偏角定義如圖2所示。
采用p個(gè)TTMD對(duì)整檔覆冰導(dǎo)線(xiàn)進(jìn)行舞動(dòng)控制,TTMD參數(shù)的優(yōu)化模型建立如下
式中 Ucri為優(yōu)化目標(biāo),即0°?α0覆冰偏角范圍內(nèi)各個(gè)覆冰偏角下起舞風(fēng)速的最小值(下文簡(jiǎn)稱(chēng)“最小起舞風(fēng)速”);X為設(shè)計(jì)變量;λdj,ζdj,sdj分別為第j個(gè)TTMD的頻率比、阻尼比、位置參數(shù)。其中頻率比(λd)定義為T(mén)TMD頻率與導(dǎo)線(xiàn)一階扭轉(zhuǎn)頻率之比,覆冰偏角α0的取值可根據(jù)導(dǎo)線(xiàn)覆冰偏角的統(tǒng)計(jì)資料確定。通過(guò)該優(yōu)化模型,在預(yù)設(shè)參數(shù)范圍內(nèi)對(duì)TTMD參數(shù)進(jìn)行優(yōu)化,使得大范圍覆冰偏角下導(dǎo)線(xiàn)最小起舞風(fēng)速實(shí)現(xiàn)最大化。
本文設(shè)計(jì)的TTMD安裝在多分裂導(dǎo)線(xiàn)的間隔棒上,目前關(guān)于間隔棒的安裝位置并無(wú)統(tǒng)一規(guī)定,因此需要考察安裝在不同位置時(shí),TTMD能實(shí)現(xiàn)的最優(yōu)控制效果。TTMD的位置參數(shù)(sd)定義為T(mén)TMD距導(dǎo)線(xiàn)端部距離與檔距的比值,sd=0.5即對(duì)應(yīng)導(dǎo)線(xiàn)跨中位置。需要注意的是,設(shè)計(jì)變量X分為兩種情況:1)X包括sd,即安裝位置是待優(yōu)化參數(shù)之一;2)X不包括sd,即在給定安裝位置前提下對(duì)TTMD參數(shù)進(jìn)行優(yōu)化。
本文采用遺傳算法搜尋最優(yōu)TTMD參數(shù)。遺傳算法是一種通過(guò)模擬生物進(jìn)化中“適者生存”的規(guī)律,采用選擇(Selection)、交叉(Crossover)和變異(Mutation)操作,從而不斷優(yōu)化每一代種群適應(yīng)度的迭代優(yōu)化算法。其原理易于理解,有較強(qiáng)的魯棒性且適用于并行計(jì)算,因此具有廣泛應(yīng)用。本文遺傳算法的選擇、交叉、變異操作分別選取輪盤(pán)賭選擇法、算數(shù)交叉法、均勻變異法。采用遺傳算法對(duì)TTMD參數(shù)的優(yōu)化設(shè)計(jì)流程如圖3所示。
優(yōu)化的主要步驟如下:
1)首先隨機(jī)生成阻尼器參數(shù)作為初始種群,設(shè)定覆冰偏角和初始風(fēng)速;
2)通過(guò)判斷TTMD?整檔導(dǎo)線(xiàn)系統(tǒng)的Jacobi矩陣特征值實(shí)部是否大于0計(jì)算得到某覆冰偏角下的起舞風(fēng)速;
3)輸出0°?α0覆冰偏角范圍內(nèi)最小起舞風(fēng)速,作為個(gè)體適應(yīng)度;
4)評(píng)估種群中所有個(gè)體適應(yīng)度并按照大小排序,通過(guò)選擇、交叉、變異等操作得到子代新個(gè)體,進(jìn)入新一輪的起舞風(fēng)速計(jì)算及適應(yīng)度評(píng)估;
5)若遺傳算法的計(jì)算滿(mǎn)足迭代終止條件,則輸出最優(yōu)阻尼器參數(shù)結(jié)果。
2 電渦流TTMD
2.1 電渦流TTMD設(shè)計(jì)
本文提出一種新型TTMD,利用電渦流原理提供可調(diào)節(jié)的線(xiàn)性阻尼,如圖4所示。TTMD內(nèi)部的銅環(huán)作為質(zhì)量元件,連接銅環(huán)與外殼的扭轉(zhuǎn)彈簧作為彈性元件,銅環(huán)與外殼上永磁體的相對(duì)運(yùn)動(dòng)所產(chǎn)生的電渦流力作為阻尼力。
TTMD的扭轉(zhuǎn)向自振圓頻率為
式中 為銅環(huán)轉(zhuǎn)動(dòng)慣量,為銅環(huán)半徑,為銅環(huán)質(zhì)量,為扭轉(zhuǎn)彈簧剛度。
由電渦流阻尼力產(chǎn)生的扭轉(zhuǎn)向阻尼比為
式中 cd為扭轉(zhuǎn)向阻尼系數(shù)。通過(guò)控制永磁體的設(shè)計(jì)參數(shù),即可實(shí)現(xiàn)所需的電渦流阻尼力、TTMD的扭轉(zhuǎn)阻尼比。
2.2 TTMD相比于TMD適用范圍的優(yōu)勢(shì)
TMD的優(yōu)勢(shì)是其構(gòu)造簡(jiǎn)單,在結(jié)構(gòu)控制方面已有較多研究及應(yīng)用。但豎向TMD的靜態(tài)伸長(zhǎng)量與線(xiàn)路結(jié)構(gòu)的自振頻率關(guān)系密切,較低的結(jié)構(gòu)頻率會(huì)造成較大的TMD伸長(zhǎng)量。對(duì)于單跨線(xiàn)路的面內(nèi)頻率,可依據(jù)下式進(jìn)行估算[17]
式中 ω為導(dǎo)線(xiàn)頻率,g為為重力加速度,EA為導(dǎo)線(xiàn)軸向剛度,H為導(dǎo)線(xiàn)張力。
假定TMD的自振頻率與線(xiàn)路頻率一致,則豎向懸掛條件下其靜態(tài)伸長(zhǎng)量為
以D型覆冰的LGJ?500/45型號(hào)導(dǎo)線(xiàn)為例,計(jì)算可得TMD靜態(tài)伸長(zhǎng)量與張力比、線(xiàn)路檔距的關(guān)系,如圖5所示。張力比為導(dǎo)線(xiàn)張力與額定拉斷力之比,相關(guān)計(jì)算參數(shù)取值參見(jiàn)文獻(xiàn)[13]。
由圖5可知,當(dāng)導(dǎo)線(xiàn)檔距大于500 m時(shí),由阻尼器自重引起的阻尼器靜態(tài)伸長(zhǎng)量可達(dá)3 m以上。隨著檔距增加,靜態(tài)伸長(zhǎng)量更大,到檔距800 m時(shí)可以達(dá)到8 m以上,這極大地限制了TMD在大檔距線(xiàn)路中的應(yīng)用。
TTMD運(yùn)行空間要求小,不存在自重引起的形變,能夠普遍適用于各種檔距的多分裂線(xiàn)路舞動(dòng)的防治,尤其可以應(yīng)用于TMD不再適用的大檔距線(xiàn)路。
3 計(jì)算設(shè)置
3.1 線(xiàn)路參數(shù)
選取特高壓工程常用的單跨八分裂導(dǎo)線(xiàn),子導(dǎo)線(xiàn)型號(hào)選用LGJ?500/45。該檔導(dǎo)線(xiàn)跨度為500 m,兩端支座高差為0。假設(shè)導(dǎo)線(xiàn)D型覆冰,通過(guò)剛性模型天平測(cè)力風(fēng)洞試驗(yàn)獲得覆冰八分裂導(dǎo)線(xiàn)氣動(dòng)力系數(shù),其Den Hartog系數(shù)和Nigol系數(shù)如圖6所示。該覆冰八分裂導(dǎo)線(xiàn)的線(xiàn)密度為23.76 kg/m,分裂間距為0.52 m,平動(dòng)阻尼比為0.44%,轉(zhuǎn)動(dòng)阻尼比為1.42%,其余相關(guān)參數(shù)參見(jiàn)文獻(xiàn)[13]。選取20階作為全局形函數(shù),計(jì)算得到導(dǎo)線(xiàn)前9階模態(tài)頻率如表1所示。
3.2 計(jì)算參數(shù)
本文針對(duì)單個(gè)TTMD研究其頻率比、阻尼比、質(zhì)量比、安裝位置、導(dǎo)線(xiàn)張力、覆冰質(zhì)量等參數(shù)對(duì)覆冰導(dǎo)線(xiàn)起舞風(fēng)速的影響。其中,頻率比、阻尼比屬于實(shí)際值易偏離設(shè)計(jì)值的阻尼器參數(shù);質(zhì)量比、安裝位置屬于設(shè)計(jì)階段確定后實(shí)際中不易發(fā)生改變的阻尼器參數(shù);導(dǎo)線(xiàn)張力、覆冰質(zhì)量屬于實(shí)際值易偏離設(shè)計(jì)值的導(dǎo)線(xiàn)參數(shù)。
質(zhì)量比(μ)定義為T(mén)TMD轉(zhuǎn)動(dòng)慣量與導(dǎo)線(xiàn)一階模態(tài)轉(zhuǎn)動(dòng)慣量之比。假定TTMD中銅環(huán)半徑為0.45 m,當(dāng)TTMD質(zhì)量比取0.02時(shí),計(jì)算可得TTMD中銅環(huán)質(zhì)量約為165 kg,占多分裂導(dǎo)線(xiàn)總質(zhì)量的1.4%,對(duì)線(xiàn)路動(dòng)力特性的影響可忽略。文獻(xiàn)[18]規(guī)定不論檔距大小平均運(yùn)行張力上限為拉斷力的25%。假定覆冰前張力比為0.25,由式(1)計(jì)算可得覆冰后張力比為0.4。本文取默認(rèn)的覆冰導(dǎo)線(xiàn)張力比為0.4。
實(shí)際觀冰監(jiān)測(cè)表明,0°?40°覆冰偏角包含了可能的導(dǎo)線(xiàn)覆冰偏角工況。因此,本文選取0°?40°覆冰偏角進(jìn)行計(jì)算,覆冰偏角間隔為1°。分別選取4階、20階全局形函數(shù),對(duì)0°?40o覆冰偏角下導(dǎo)線(xiàn)起舞風(fēng)速進(jìn)行計(jì)算,結(jié)果表明在所有覆冰偏角下二者的起舞風(fēng)速相差均不超過(guò)0.2 m/s。在后續(xù)遺傳算法優(yōu)化計(jì)算中,為提高計(jì)算效率并兼顧計(jì)算精度,選取4階全局形函數(shù)參與計(jì)算。
式(9)的約束條件中,遺傳算法所用變量的搜尋范圍定義為
遺傳算法相關(guān)計(jì)算參數(shù)如表2所示。以質(zhì)量比0.02為例,TTMD優(yōu)化計(jì)算結(jié)果如圖7所示。由圖可知,遺傳代數(shù)為10時(shí)結(jié)果已基本收斂,后續(xù)計(jì)算中遺傳代數(shù)均取20。
本文的計(jì)算工況如表3所示。工況可分為三類(lèi):(a)給定相關(guān)參數(shù),優(yōu)化TTMD參數(shù);(b)給定相關(guān)參數(shù),評(píng)估控制效果對(duì)TTMD參數(shù)的魯棒性;(c)給定TTMD最優(yōu)參數(shù),研究結(jié)構(gòu)參數(shù)不確定性對(duì)控制效果的影響。
4 結(jié)果分析
4.1 控制效果驗(yàn)證
根據(jù)李雅普諾夫第一穩(wěn)定定理計(jì)算可得40°覆冰偏角下起舞風(fēng)速為11.2 m/s。采用Newmark?β法計(jì)算得到40°覆冰偏角、11 m/s和12 m/s風(fēng)速下導(dǎo)線(xiàn)跨中運(yùn)動(dòng)時(shí)程如圖8所示,由幅值發(fā)散情況判斷舞動(dòng)發(fā)生情況。結(jié)果表明Newmark?β法計(jì)算得到的舞動(dòng)發(fā)生情況與李雅普諾夫第一穩(wěn)定定理計(jì)算結(jié)果一致,說(shuō)明了本文方法的正確性。
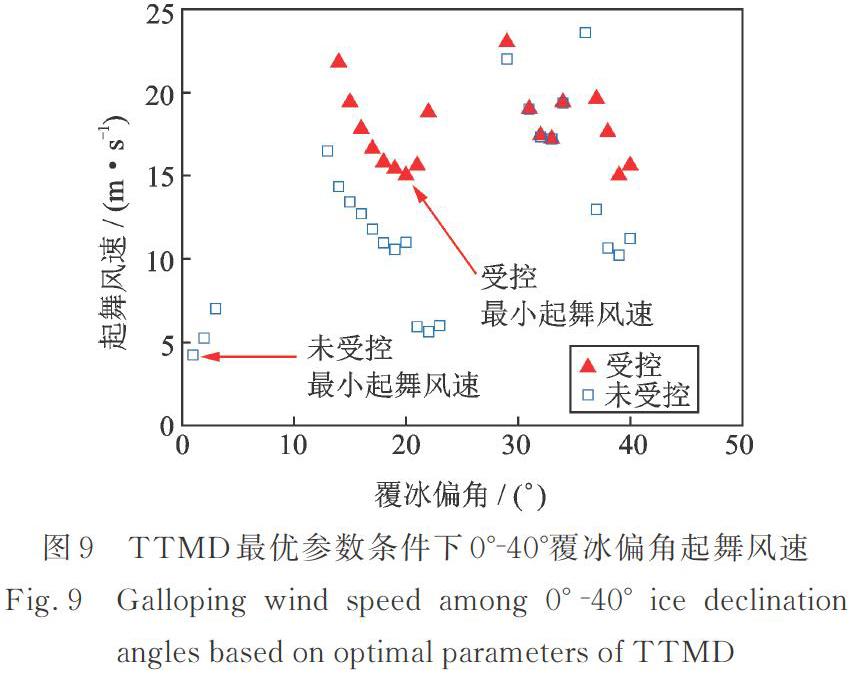
取質(zhì)量比0.02,對(duì)TTMD的頻率比、阻尼比、位置等參數(shù)進(jìn)行優(yōu)化,所得最優(yōu)頻率比為0.81,最優(yōu)阻尼比為0.18,最優(yōu)位置參數(shù)為0.39,不同覆冰偏角下起舞風(fēng)速如圖9所示。由圖可知,未受控導(dǎo)線(xiàn)的最小起舞風(fēng)速為4.2 m/s,而TTMD控制下最小起舞風(fēng)速提高至15 m/s,且大部分覆冰偏角下的起舞風(fēng)速得到顯著提高。這表明TTMD能夠有效控制大范圍多覆冰偏角下導(dǎo)線(xiàn)的舞動(dòng)。
4.2 TTMD控制優(yōu)化結(jié)果
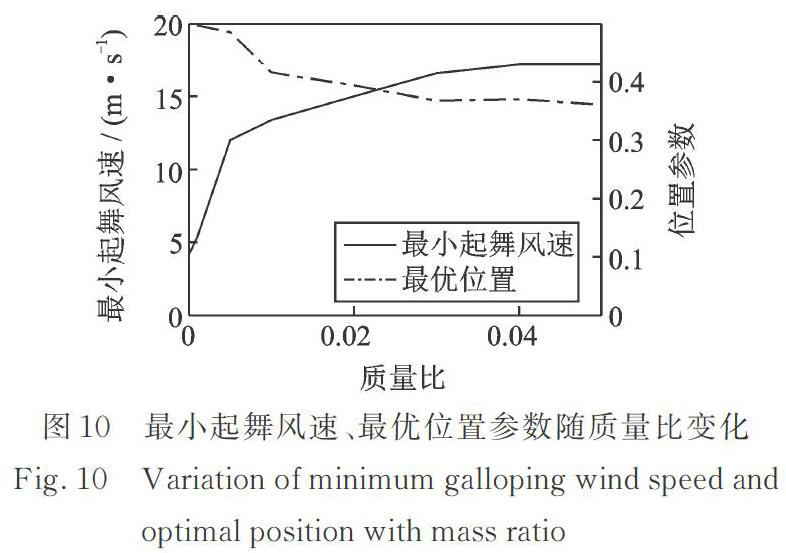
基于不同的質(zhì)量比,對(duì)TTMD的頻率比、阻尼比、位置等參數(shù)進(jìn)行優(yōu)化,所得最小起舞風(fēng)速及相應(yīng)的最優(yōu)位置參數(shù)如圖10所示。
如圖10所示,最小起舞風(fēng)速隨著質(zhì)量比的增大而持續(xù)增大。當(dāng)質(zhì)量比為0.005時(shí),最小起舞風(fēng)速的控制效果已經(jīng)較為顯著,提升了7.8 m/s。當(dāng)質(zhì)量比高于0.03時(shí),最小起舞風(fēng)速的上升趨勢(shì)不明顯。另外,隨著質(zhì)量比的增大,相應(yīng)的最優(yōu)位置從跨中逐漸向端部偏移,最后穩(wěn)定在0.36?0.39的位置參數(shù)區(qū)間。
分別取質(zhì)量比0.01,0.02,0.04,沿整檔導(dǎo)線(xiàn)取不同安裝位置,對(duì)TTMD的頻率比、阻尼比參數(shù)進(jìn)行優(yōu)化,結(jié)果如圖11所示。由于覆冰分裂導(dǎo)線(xiàn)?TTMD系統(tǒng)對(duì)跨中位置具有對(duì)稱(chēng)性,圖中僅展示位置參數(shù)0?0.5的部分。如圖11所示,在TTMD從線(xiàn)路端部向跨中移動(dòng)過(guò)程中,各質(zhì)量比條件下的最小起舞風(fēng)速表現(xiàn)出相似的變化趨勢(shì):最小起舞風(fēng)速首先保持穩(wěn)定,然后快速增大,并在0.37?0.41位置區(qū)間內(nèi)達(dá)到最大值,隨后減小。總體而言,在各質(zhì)量比條件下,TTMD在導(dǎo)線(xiàn)左側(cè)1/4跨?右側(cè)1/4跨(即位置參數(shù)0.25至0.75)范圍內(nèi)均能實(shí)現(xiàn)良好的起舞風(fēng)速控制效果。
4.3 TTMD參數(shù)魯棒性分析
分別取質(zhì)量比0.01,0.02,0.04及相應(yīng)的最優(yōu)位置參數(shù),計(jì)算TTMD在不同頻率比、阻尼比參數(shù)下最小起舞風(fēng)速,結(jié)果如圖12所示。令質(zhì)量比為0.02,基于不同的位置參數(shù),計(jì)算TTMD在不同頻率比、阻尼比參數(shù)下最小起舞風(fēng)速,結(jié)果如圖13所示。
如圖12所示,TTMD的最小起舞風(fēng)速在頻率比、阻尼比參數(shù)空間內(nèi)表現(xiàn)出明顯的“尖峰”特征,在尖峰范圍內(nèi),最小起舞風(fēng)速維持在較高的水平。質(zhì)量比0.02條件下,尖峰對(duì)應(yīng)的頻率比范圍為0.7?0.84,阻尼比范圍為0.16?0.3,這就是TTMD能實(shí)現(xiàn)良好控制效果的參數(shù)范圍。隨著質(zhì)量比的增大,最小起舞風(fēng)速的峰值范圍明顯擴(kuò)大,因此提高質(zhì)量比可以提高TTMD對(duì)于舞動(dòng)風(fēng)速抑制的魯棒性。
圖13中,在位置參數(shù)0.39條件下,最小起舞風(fēng)速的最大值為15 m/s,在3個(gè)位置中表現(xiàn)最優(yōu),且TTMD表現(xiàn)出較強(qiáng)的魯棒性。比較位置參數(shù)0.3,0.5可知,二者最小起舞風(fēng)速的尖峰值較為接近,而位置參數(shù)0.5的尖峰明顯更寬,TTMD魯棒性更強(qiáng),這表明同等起舞風(fēng)速控制水平下,TTMD安裝在靠近跨中的位置比靠近端部的位置具有更強(qiáng)的魯棒性。
4.4 結(jié)構(gòu)參數(shù)不確定性影響
線(xiàn)路運(yùn)行過(guò)程,導(dǎo)線(xiàn)張力、覆冰質(zhì)量會(huì)有一定變化,偏離優(yōu)化設(shè)計(jì)的預(yù)設(shè)值。為研究導(dǎo)線(xiàn)張力、覆冰質(zhì)量變動(dòng)的影響,分別取質(zhì)量比0.01,0.02和0.04,且基于位置參數(shù)0.39與覆冰后張力比0.4,優(yōu)化得到TTMD最優(yōu)參數(shù);根據(jù)最優(yōu)參數(shù),分別計(jì)算導(dǎo)線(xiàn)張力、覆冰質(zhì)量變化情況下TTMD對(duì)起舞風(fēng)速的控制效果,結(jié)果分別如圖14和15所示。
如圖14所示,對(duì)于未受控導(dǎo)線(xiàn)以及各質(zhì)量比條件下的受控導(dǎo)線(xiàn),隨著導(dǎo)線(xiàn)張力比增大,其最小起舞風(fēng)速均呈下降趨勢(shì),這表明本文選取覆冰前張力比的上限0.25(覆冰后張力比0.4)是較為安全的。因此,在TTMD的初步設(shè)計(jì)階段,應(yīng)當(dāng)選取較大的張力條件進(jìn)行計(jì)算。
圖15表明,對(duì)于未受控導(dǎo)線(xiàn)以及各質(zhì)量比條件下的受控導(dǎo)線(xiàn),隨著覆冰質(zhì)量的增大,最小起舞風(fēng)速均持續(xù)增大。因此,基于較小的覆冰質(zhì)量條件進(jìn)行TTMD參數(shù)的優(yōu)化設(shè)計(jì)是較為安全的選擇。
5 結(jié) 論
本文針對(duì)大檔距特高壓輸電線(xiàn)路舞動(dòng)防治設(shè)計(jì)了一種扭轉(zhuǎn)向調(diào)諧質(zhì)量阻尼器(TTMD)。建立整檔覆冰導(dǎo)線(xiàn)?TTMD系統(tǒng)的運(yùn)動(dòng)方程,采用李亞普諾夫穩(wěn)定定理求解起舞風(fēng)速;建立基于遺傳算法的TTMD防舞優(yōu)化設(shè)計(jì)方法,以大范圍多覆冰偏角下導(dǎo)線(xiàn)最小起舞風(fēng)速為優(yōu)化目標(biāo);以某大檔距特高壓輸電線(xiàn)路覆冰八分裂導(dǎo)線(xiàn)為例,對(duì)TTMD各項(xiàng)參數(shù)進(jìn)行優(yōu)化設(shè)計(jì),主要結(jié)論如下:
1)TTMD相比于豎向TMD沒(méi)有豎向行程限制,在大檔距特高壓線(xiàn)路中的應(yīng)用具有顯著優(yōu)勢(shì)。
2)本文提出的TTMD防舞優(yōu)化設(shè)計(jì)方法可有效提高大范圍多覆冰偏角的導(dǎo)線(xiàn)起舞風(fēng)速。質(zhì)量比高于0.005時(shí),TTMD即可實(shí)現(xiàn)良好的防舞效果。
3)應(yīng)用整檔導(dǎo)線(xiàn)模型實(shí)現(xiàn)了對(duì)TTMD安裝位置的優(yōu)化。總體而言,TTMD安裝在導(dǎo)線(xiàn)左側(cè)1/4跨?右側(cè)1/4跨范圍內(nèi)任意位置均能實(shí)現(xiàn)良好的起舞風(fēng)速控制效果。
4)TTMD對(duì)導(dǎo)線(xiàn)的起舞控制效果具有良好的魯棒性。
5)在TTMD的設(shè)計(jì)階段,應(yīng)采用較高的導(dǎo)線(xiàn)張力、較小的覆冰質(zhì)量設(shè)定,以得到偏于安全的TTMD參數(shù)設(shè)計(jì)值。
參考文獻(xiàn):
[1] 樓文娟, 余 江, 姜 雄, 等. 覆冰六分裂導(dǎo)線(xiàn)舞動(dòng)風(fēng)洞試驗(yàn)及起舞風(fēng)速研究[J]. 振動(dòng)工程學(xué)報(bào), 2017, 30(2):280-289.
Lou Wenjuan, Yu Jiang, Jiang Xiong, et al. Wind tunnel test and critical wind speed study for galloping of 6-bundled iced conductors[J]. Journal of Vibration Engineering, 2017, 30(2):280-289.
[2] Hartog J P D. Transmission line vibration due to sleet [J]. Transactions of the American Institute of Electrical Engineers, 1933, 51(4):1074-1076.
[3] Nigol O, Buchan P. Conductor galloping part I - Den Hartog mechanism [J]. IEEE Transactions on Power Apparatus & Systems, 1981, PAS-100(2):699-707.
[4] Yu P, Shah A H, Popplewell N. Inertially coupled galloping of iced conductors [J]. Journal of Applied Mechanics, 1992, 59(1):140.
[5] 姜 雄, 樓文娟. 三自由度體系覆冰導(dǎo)線(xiàn)舞動(dòng)激發(fā)機(jī)理分析的矩陣攝動(dòng)法[J]. 振動(dòng)工程學(xué)報(bào), 2016,29(6):1070-1078.
Jiang Xiong, Lou Wenjuan. Matrix perturbation method for analysis of 3 DOF iced transmission line galloping mechanism[J]. Journal of Vibration Engineering, 2016,29(6):1070-1078.
[6] Xu Z D, Xu L Z, Xu F H. Study on the iced quad-bundle transmission lines incorporated with viscoelastic antigalloping devices [J]. Journal of Dynamic Systems, Measurement, and Control, 2015, 137(6):061009.
[7] Guo H, Liu B, Yu Y, et al. Galloping suppression of a suspended cable with wind loading by a nonlinear energy sink[J]. Archive of Applied Mechanics, 2017, 87(6):1007-1018.
[8] 嚴(yán) 波, 胡 景, 周 松, 等. 隨機(jī)風(fēng)場(chǎng)中覆冰四分裂導(dǎo)線(xiàn)防舞研究[J]. 振動(dòng)與沖擊, 2011, 30(7):52-58.
Yan Bo, Hu Jing, Zhou Song, et al. Anti-galloping for an iced quad-bundled conductor in stochastic wind field [J]. Journal of Vibration and Shock, 2011, 30(7):52-58.
[9] 胡 景, 嚴(yán) 波, 祖正華, 等. 一種新型防舞器及其機(jī)理研究[J]. 工程力學(xué), 2011, 28(9):200-206.
Hu Jing, Yan Bo, Zu Zhenghua, et al. A new anti-galloping device and investigation on its mechanism [J]. Engineering Mechanics, 2011, 28(9):200-206.
[10] Hervé Pohsié G, Chisari C, Rinaldin G, et al. Application of a translational tuned mass damper designed by means of genetic algorithms on a multistory cross-laminated timber building[J]. Journal of Structural Engineering, 2015, 142(4): E4015008.
[11] 陳 鑫, 李?lèi)?ài)群, 徐慶陽(yáng), 等. 基于遺傳算法的高聳結(jié)構(gòu)環(huán)形TLD滿(mǎn)意優(yōu)化設(shè)計(jì)[J]. 工程力學(xué), 2016, 33(6):77-84.
Chen Xin, Li Aiqun, Xu Qingyang, et al. Satisfaction optimum design of ring-shape TLD control for high-rise structure using genetic algorithm [J]. Engineering Mechanics, 2016, 33(6):77-84.
[12] 劉海英, 張琪昌, 郝淑英. 覆冰四分裂輸電線(xiàn)舞動(dòng)研究[J]. 振動(dòng)工程學(xué)報(bào), 2011,24(3):19-23.
Liu Haiying, Zhang Qichang, Hao Shuying. A study on galloping for iced quad-bundled conductor[J]. Journal of Vibration Engineering, 2011,24(3):19-23.
[13] Lou W, Huang C, Huang M, et al. An aerodynamic anti-galloping technique of iced 8-bundled conductors in ultra-high-voltage transmission lines[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2019, 193:103972.
[14] 邵天曉. 架空送電線(xiàn)路的電線(xiàn)力學(xué)計(jì)算[M]. 北京: 中國(guó)電力出版社, 2003.
[15] 陳立群, 劉延柱. 非線(xiàn)性振動(dòng)[M]. 北京: 高等教育出版社, 2001.
[16] Qin Z, Chen Y, Zhan X, et al. Research on the galloping and anti-galloping of the transmission line [J]. International Journal of Bifurcation and Chaos, 2012, 22(2):1250038.
[17] Irvine H M. Cable Structures[M]. Cambridge, MA: MIT Press, 1981.
[18] 中國(guó)電力企業(yè)聯(lián)合會(huì). GB 50545-2010,110 kV~750 kV架空輸電線(xiàn)路設(shè)計(jì)規(guī)范[S].北京:中國(guó)計(jì)劃出版社,2010.
China Electricity Council. GB 50545-2010, Code for design of 110 kV~750 kV overhead transmission line[S]. Beijing: China Planning Press, 2010.
作者簡(jiǎn)介: 樓文娟(1963-),女,教授。 E-mail: louwj@zju.edu.cn

