窮理盡性,提高運算能力
謝彧杰
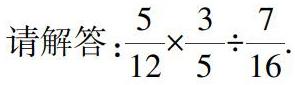
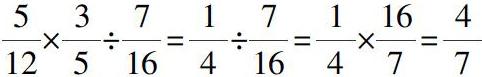

【摘要】從說理中培養學生的數學運算能力,對學生思考和探究數學運算知識起到了重要的作用.但如何讓學生充分說理,引導學生使用正確的數學語言來表達問題,展開運算知識的交流,仍需要教師思考和探究出有效的教學方式,唯有如此,才能有效指導學生在說理的過程中提高自身的數學運算能力.本文基于學生說理的角度,對學生的數學運算能力展開教學培養研究.
【關鍵詞】數學運算;說理;方法;研究
前?言
學習數學運算知識不能只是簡單地死記硬背運算定理,而應懂得運用數學運算知識進行說理,這樣學生的學習才更有效果,更有效率.本文從學生說理層面對學生的數學運算能力展開研究,從而在研究的過程中,及時了解學生的說理和運算能力,進而針對學生的說理和運算弱點,提出有效的數學運算教學方法和說理方法,最終引導學生有效說理,有效運算.
一、學生說理與數學運算
(一)說理加深學生對運算題的理解
由于學生的學習時間比較緊湊,導致他們無法對問題進行深入思考.尤其是在解答數學運算題目的過程中,很多學生拿到題目就立即做題,沒有花費過多的時間來運用數學知識進行運算問題的說理,這樣不利于學生有效理解數學運算題.那么通過引導學生充分說理數學運算題,會促使學生對數學運算題目中的因果關系展開深入的思考和探究,并由此幫助學生構建一個感性的觀念,從而有效加深學生對數學題目的理解,進而提升學生的數學運算解題能力.因此,引導學生說理對提升他們自身的數學運算能力具有一定的作用.
(二)說理提升學生的運算解答興趣
學生說理數學運算題目,是對數學題目中的因果邏輯關系由因到果的一個講述過程,其可以有效培養學生的感性認識,使得學生對數學運算題目有一定的探究和解答興趣,從而促使他們更好地分析和表達自己對數學運算題目的理解.因此,適當引導學生參與到數學運算的說理過程中,對提升學生的數學運算解答興趣可以起到積極的作用,也有利于促使學生從說理的過程中逐漸形成良好的數學運算知識的認知能力.教師應該借助說理的方式,由說理來強化學生的運算解答能力[2].
(三)說理增強學生運算知識運用能力
說理只有基于學生自身的理解能力和基礎知識水平,才能有效地對問題的因果關系進行講述,因而學生必須掌握一定的基礎知識、語言表達能力,這樣才能有效講述自己對問題的理解和認知.在數學運算過程中,學生對某個數學運算問題進行說理,體現出學生自身已經具備了一定的數學運算基礎知識,且有一定的能力運用自身所學的數學運算知識來解答數學問題.因此,培養學生的說理能力也是增強學生數學運算知識運用能力的有效途徑.
二、學生說理以及數學運算能力的培養過程
(一)強化學生的數學運算基礎知識
無論學生是在說理數學運算問題,還是在解答數學運算問題,都必須具備良好的數學運算基礎知識,只有這樣才能有效運用數學運算知識來進行運算題目的說理.因此,在對學生說理以及數學運算能力培養之前,教師應該有效引導學生做好數學運算基礎知識的理解和認知,促使他們打好知識基礎,從而為數學運算問題的說理和解答做好準備.教師可以先從數學運算基礎知識出發,加強學生對數學運算概念、運算公式、運算法則及其性質展開學習與記憶.當學生正式進行數學運算說理和解答時,就可以有效運用運算公式及法則進行題目的因果關系說理,從而運用正確的數學運算語言進行問題的解答表述.
以數學運算教學中的“分數混合運算”知識為例,在對學生數學運算能力培養之前,教師應該要求學生熟練掌握分數、混合運算的順序、方法等有關概念,在概念認知基礎上引導學生運用概念知識來解答實際的數學運算問題,并要求學生嘗試利用相關的數學語言進行講述,由此鍛煉學生的數學說理和運算能力.然后,教師應給予學生一定的時間去分析與記憶有關內容,從而把握好分數混合運算的依據、方法與步驟,進而讓學生認真學習相關的算法,最終培養學生的數學運算能力.我們以下面這道題目為例:
解答分析:在進行關于分數混合運算的過程中,教師應該引導學生充分說理運算題目,即讓學生說一說題目涉及哪些數學運算法則、定律、概念知識等,以促使學生能夠利用關于分數混合運算的數學語言進行運算問題的解答,從而加強學生的知識運用和表述能力,使學生懂得在分數混合運算解答中可以運用哪些運算法則及定律知識[3].上述例題涉及了分數混合運算的約分、倒數等基礎知識,因而在說理過程中,學生應該依據題目分析分數混合運算的順序,并將題目中的定律知識也表述出來.
解答過程:本題屬于同級運算,因而應該從左到右依次進行計算,同時進行約分和改寫題目中的除號;而在改寫除號時,要懂得“除以一個數等于乘以這個數的倒數”的運算定律.所以,該道問題的解答方法如下:
基于這些性質定理知識,學生應該先嘗試自己去分析和說理問題,試著花費一些時間將題目中的分數混合運算內容運用數學相關的性質和定理進行說理,從而促使學生能夠充分理解問題,進而快速地計算出運算題的答案.
(二)結合實際問題進行運算說理及解答
培養學生的說理和數學運算能力,除了要提升學生的運算基礎知識能力外,還要注意引導學生合理利用時間,進行高效的數學運算說理和運算.其中,教師可以利用實踐教學的方式,根據學生的學習能力和運算基礎知識水平,提出一些數學應用問題,從讓學生利用所學的運算知識進行問題的解答,進而強化學生對數學運算知識的理解和運用[4].
以下面這道數學運算題目為例:某個學校中的教學大樓高36米,現在小明制作了一個學校教學大樓模型,其中模型的高度與實際高度的比是1∶30,則模型的高度應是多少米?
解題分析:這是一道較為基礎的數學比例運算問題.解答這道問題時,學生要懂得從題目中蘊含的數學運算知識出發,對問題進行有效說理,以分析出題目中到底涉及哪些數學原理知識,如何運用這些基礎知識進行問題因果關系的邏輯分析.其中,學生可以利用題目中的比,即1∶30這個已知條件,并基于比例概念知識,構建比例關系,求解出比例中的未知項.
解答過程:設模型高度為x米.
x∶36=1∶30
30x=36
x=1.2
在解答過程中,教師要給予學生一定的時間,讓學生從比例關系說理如何構建題目中的數學運算等式,從而促使學生懂得利用所學的比例知識進行數學運算問題的解答.
(三)組織說理和數學運算反思環節
在學生數學運算能力培養的過程中,教師需要引導學生做好課后的反思學習,讓學生能夠對自身存在的學習問題進行及時評價、糾錯.以數學中的幾何問題運算為例,對于學生而言,立體幾何是一項重要且比較難理解的數學知識點,尤其是在解答幾何運算問題時,很多學生感覺到運算比較吃力.所以,教師對學生展開運算說理以及訓練時,應該組織相關的反思學習環節,幫助學生找到自身存在的弱點,并及時幫助學生克服學習問題,有效提升學生的運算能力.
比如下面這道例題:如下圖所示,已知平行四邊形中空白部分的面積為80平方厘米,請求出圖中陰影部分的面積.
解題分析:學生應該學會利用所學的平行四邊形定理、面積計算等知識進行問題的說理,明確題目中涉及哪些幾何圖形的性質定理知識,并學會利用平行四邊形的相關知識進行問題的說理,以分析題目中空白與陰影部分面積的邏輯關系,從而由題目中空白部分面積的已知條件去分析陰影部分面積,進而尋找到二者之間的邏輯關系.
解答過程:16×7=112(m2)
112-80=24(m2)
從解答過程中,學生也要懂得反思自己是否充分理解平行四邊形的有關定理知識,以及平行四邊形的面積計算方法,從而能夠在面積計算中加深對平行四邊形知識的理解和認知[5].
三、結語
綜上所述,說理與數學運算教學的融合,既可以強化學生對運算知識的理解和認知,也能促使學生在說理過程中提升自身的數學知識表達能力,這對全面提升學生的數學運算能力起到了積極的作用.其中,教師可以先從學生的運算基礎知識水平出發,結合適當的運算知識以及反思環節,幫助學生做到充分說理和有效運算.
【參考文獻】
[1]錢曉燕.立足數學核心素養,培養學生運算能力[J].學苑教育,2017,5(21):48.
[2]李錦珠.基于說理能力培養下數學教學策略探討[J].考試周刊,2019,13(25):52-53.
[3]陳運兵.如何在數學教學中培養學生的說理能力[J].信息周刊,2019,22(3):174.
[4]周順全.培養和發展學生數學運算能力的有效途徑[J].讀寫算,2019,5(22):263.

