在計算中學習基本的數學思想方法

劉梅

“基本的數學思想方法”作為小學生數學學習的目標之一，要求學生既要學習數學知識，又要學習數學方法。然而，在小學數學計算課教學中，經常會過于偏重于技能訓練，從而忽視計算中蘊涵的基本數學思想方法。在計算中學習轉化、類比、數形結合、歸納等方法，不僅有利于學生理解算理，掌握算法，形成良好的認知結構，而且還有利于發展學生的邏輯思維能力，為后續學好數學打下基礎。

一、構建聯系，實現轉化

教學中，當不能或不易直接應用已有知識解決問題時，教師要根據數學知識之間的邏輯聯系，引導學生將要解決的問題不斷轉化，最終實現對原問題的解決。在計算課中，學習用轉化方法思考問題，有助于良好思維習慣的培養。

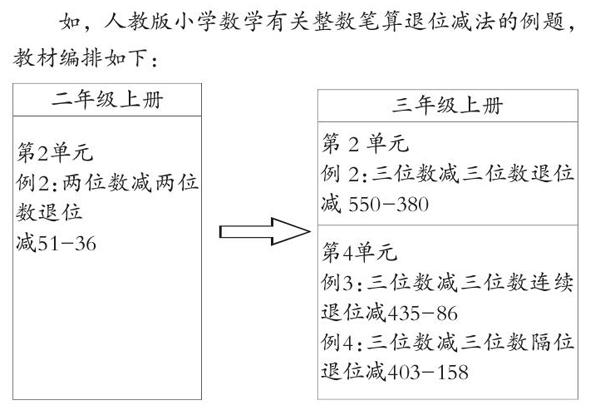
如，人教版小學數學有關整數筆算退位減法的例題，教材編排如下：

通過以上4個例題的學習，豐富學生將退位減轉化為不退位減的學習經驗。學習51-36時，產生一個認知沖突，個位上的1減6不夠減，該怎么辦？教師要抓住這個時機，幫助學生構建退位減與不退位減知識之間的聯系，用轉化方法解決退位減的問題。為促進學生邏輯思維的發展，提出怎樣轉化？為此，調動學生100以內兩位數減一位數的學習經驗，從十位分出1個十，轉化為10個一，退給個位，個位上的數從1個一變為11個一，實現了個位從不夠減到夠減的轉化。學生經歷轉化——怎樣轉化的學習過程后，反思為什么要轉化，讓學生在表達中感受將新的知識轉化為學生已經學過的知識，并利用已經學過的知識高效學習新知的思想方法。這種方法一直接延續到三年級上冊退位減的三個例題中：

筆算550-380，十位上的5減8不夠減，怎么辦？用轉化的方法解決，從百位上分出1個百，轉化為10個十，退給十位，十位上的數從5個十變為15個十。

筆算435-86，當個位不夠減轉化為夠減時，十位上的數為什么是2？當十位不夠減轉化為夠減時，十位上的數為什么是12？

筆算403-158，在兩次轉化的過程中，十位上的數發生幾次變化？怎樣變化？

這樣學習，不僅讓學生深度理解、掌握退位減的方法，更重要的是凸顯轉化在計算中的價值。逐漸讓學生學會在新、舊知識的轉化中尋找到解決“新”知的方法。

二、比較相似，遷移類比

數學教育家波利亞說：“類比就是一種相似。”通過觀察、比較發現新、舊知識具有相似的性質時，就可以把已有知識類比到新知識的學習過程中，得到一個新的結論。

小數除法計算對小學生來講是一個難點，如何解決這個問題呢？從整體的角度比較有余數的除法、除數是一位數的整數除法、除數是二位數的整數除法、除數是整數的小數除法、除數是小數的小數除法，發現它們筆算除法的方法是相似的，都是用除法豎式記錄平均分的過程，每次分都是把余數的計數單位變小和更低一位上的數合并繼續平均分。由此可見，教師可以引導學生用類比的方法學習整數、小數筆算除法。

如，五年級上冊第三單元小數除法例1（22.4÷4），分以下三個環節開展學習活動：

先呈現224÷4的除法豎式，交流第二次平均分的方法、過程及結果。即：把2個十平均分成4份，不夠分1個十，就把2個十轉化為更小的計數單位也就是20個一，再和4個一合并為24個一。這樣就把2個十平均分成4份轉化為把24個一平均分成4份，商是6個一，商6寫在個位上。

接下來讓學生比較筆算224÷4與22.4÷4有什么相似之處？都是筆算除法，都用除法豎式記錄每一次平均分的過程及結果，且平均分的方法不變，那么就可以把筆算224÷4的方法類比到22.4÷4中。

最后呈現學習單，讓學生帶著任務和要求自主學習。

顯然，學習例1，不僅要掌握除數是整數的小數除法筆算方法，更重要的是學習用類比方法思考第二次是把2個一平均分成4份轉化為把24個十分之一平均分成4份的過程，從而類推出商的小數點為什么要點在十分位6的左下角。

從以上學習過程可以看出，盡管不同單元的學習內容有難易之分，但貫穿于其中的轉化及類比思想是不變的。有了類比的思想方法，學生就會感受到整個小學階段筆算除法的知識不是孤立和零散的，而是一個相互有關聯的統一整體，把握好變與不變，不僅有助于發展學生類比推理的能力，而且還有助于學生形成良好的認知結構。

三、直觀感知，數形結合

數形結合思想是根據數與形之間的對應關系和相互轉化來解決問題的思想方法。在計算課中，有的學習內容需要借助計數器、小棒、圖形建立形的直觀，理解“數”的含義及算的原理，進而讓學生體會以形助數的思想方法。

如，二年級下冊有余數的除法例3：13根小棒，每4根分一組，結果怎樣？

先操作分的過程和結果，理解圖式的含義;再將操作的過程及結果寫成除法橫式，借助形的直觀感知除法橫式中13、4、3、1表示的含義;最后提出除法橫式也可以寫成豎式，構建除法橫式與豎式的聯系，并將以形助數的學習經驗再一次類比到除法豎式中，理解12表示分掉的12根小棒，12下面的橫線及1表示分了之后還余1根小棒。這樣從直觀操作到除法橫式到除法豎式的轉化，構建了知識之間的內在聯系，實現了從直觀到抽象的學習過程，為后續學習三年級除數是一位數的整數除法打下基礎。

另外，還可以充分畫圖，引導學生從分數意義的角度直觀理解分數加、減、乘、除運算的法則。比如，理解同分母分數加法法則，學生借助圖形得出+=后，教師提出問題，分母為什么是8？分子為什么是4？解決這兩個問題，就要運用形的直觀感知3個和1個相加，結果是（3+1）個，即，再引導學生從分數的意義直觀理解分母是8，分子是3+1的算理。把這樣的方法類比到任意兩個同分母分數相加，豐富學生以形理解“分母不變、分子相加”的活動經驗，從而抽象出同分母加法的計算法則。

小學生的思維以直觀形象思維為主，理解運算法則中每一個數或每一步的算理時，通常是化抽象為直觀，突出數與形的對應，逐漸體會以形理解數或算理的學習方法。

四、分析共性，歸納概括

歸納是特殊到一般的推理形式。小學數學一般采用不完全歸納，依據一類事物中部分對象的相同性質推出該類事物都具有這種性質的一般結論的推理方法。在計算中，歸納一般表現在以下兩個方面：

一是讓學生在經歷數學知識形成的過程中學習歸納的方法。前面講到列加法豎式，在操作感知的基礎上，引導學生分析5和2都寫在個位上，抽象出都寫在相同的數位——個位上，且要對齊寫;3和3都寫在十位上，抽象出都寫在相同的數位——十位上，同樣要對齊寫。此時，學生就會發現一個共同的本質屬性，所寫的數位是“相同”的，且要對齊寫，自然歸納出相同數位要對齊這一個數學結論。二是學生既要從某類事物個別對象中發現其共同的因素，也要發現對象之間的聯系，在廣泛的聯系中突出事物的本質特征。

如，“多位數乘一位數”不僅要從整體上分析每一個例題的重、難點，同時還要理解例題之間的內在聯系，便于更好地歸納出多位數乘一位數的計算法則。

學習例1時，重點表達用第二個因數分別去乘第一個因數的個位、十位、百位，再把兩次或三次乘的積相加，在表達中感悟出依次、每一位的含義。

學習例2、例3時，重點表達個位滿幾十向十位進幾、十位滿幾十向百位進幾，百位滿幾十向千位進幾的方法，在表達中感悟哪一位、前一位的含義。

通過表達，突出每一個詞的含義，突出計算的基本步驟和要點，學生就能歸納概括出多位數乘一位數的計算法則。

計算中融入基本的數學思想方法，不僅能夠提高學生的運算能力，更重要的是豐富了學生用轉化、類比、數形結合、歸納等方法學習數學的經驗，促進學生邏輯思維的發展，真正體現計算育人的價值。