基于二維耦合映像格子模型的圖像加密

王 永 ，江功坤 ，尹恩民

（1. 重慶郵電大學計算機科學與技術學院，重慶 400065；2. 桂林電子科技大學廣西密碼學與信息安全重點實驗室，廣西 桂林 541004）

混沌與密碼學之間存在著普遍的相似性，這使得基于混沌的密碼學成為熱門研究之一，如混沌流密碼[1]、混沌Hash 函數[2]、混沌S 盒[3]和混沌圖像加密[4-10]. 由于數字圖像在軍事、醫療、商業等各領域的普遍應用，其安全性研究受到廣泛重視. 而傳統的加密方案，如AES （advanced encryption standard）、DES（data encryption standard）等，對數字圖像并不適用，使得基于混沌的圖像加密方案逐漸受到研究者們的青睞.

混沌系統的選擇對于混沌圖像加密算法來說至關重要. 混沌系統一般可以分為一維混沌系統[11-12]和高維混沌系統[13-14]兩大類. 時空混沌是一種復雜的混淆系統，它在圖像加密中的應用日益廣泛. 文獻[15]運用耦合映像格子設計偽隨機位序列生成器，并提出了一種基于偽隨機比特序列和DNA （deoxyribo nucleic acid）編碼的加密算法. 文獻[16]提出了一種基于自適應動態密鑰流提取技術的塊混沌圖像加密算法，該算法將時空混沌系統與Tent-Sine 系統相結合來生成混沌序列，并以此為基礎加密圖像. 從當前的研究看，從混沌系統中抽取的混沌序列在圖像加密過程中發揮了重要的作用，對整個加密算法的安全性至關重要. 雖然選擇高維或者復雜的混沌系統能夠保證所產生序列的復雜性，有效防止攻擊者對序列的預測與重構，但是，這些復雜混沌系統的狀態值在相空間的分布往往是不均勻的，從而為攻擊者進行統計攻擊或者暴力攻擊提供了便利. 文獻[17]正是利用了這種不足，對一種基于DNA 編碼和時空混沌的圖像加密算法實施了有效的攻擊.

針對上述安全問題，本文將分段時空混沌與暫態變換結合，構造了一個新的混沌模型T2DCML（T-2D coupled map lattices）. 該模型以分段混沌系統作為局部映射，很好地平衡了系統復雜性和效率之間的關系. 同時，利用暫態變換實現了模型狀態值的均勻分布，保證了其所產生的混沌序列的高度安全性. 基于T2DCML 模型，本文進一步提出了一種圖像加密算法. 該算法依據矩陣變換簡化了圖像的置亂操作，無需如傳統的混沌置亂方法那樣對矩形圖像預處理，增強了算法的適用性. 仿真實驗及性能分析表明，該算法能夠有效保證圖像加密的安全性，滿足圖像在網絡中安全傳輸的需求.

1 混沌模型

1.1 二維耦合映像格子模型

耦合映像格子（coupled map lattices，CML）模型是一類典型的時空混沌模型，在混沌密碼中得到逐步廣泛的應用. 為了進一步增強模型的復雜性，一維CML 模型被擴展到了二維CML （2DCML）模型，其常用的數學表達式如式（1）.

將式（3）所示的分段Logistic 映射（piecewise logistic map，PLM）選為2DCML 模型的局部混沌函數，因為它具有比Logistic映射更大的李雅普諾夫指數（Lyapunov exponent，LE）[18]，能夠更好地保證模型的復雜性.

1.2 2DCML 模型的性能分析

1.2.1 李雅普諾夫指數

根據文獻[19]的研究結果，可得式（2）所描述的2DCML 模型的LE 解析式為

由式（4）知，當i=R，j=L時，模型的LE 取得最大值. 即2DCML 的最大LE 由局部混沌函數PLM的LE 決定. 為了保證模型具有復雜的動力學行為，本文設置 μ = 4. 同時，PLM 模型的LE 與分段數N的關系如圖1 所示. 由圖1 中可知：不論N取何值，PLM 的LE 均為正數，并且隨著N的增大而增大. 這說明PLM 作為2DCML 的局部函數能夠很好保持該模型整體的混沌特性. 在權衡PLM 的保持良好非線性和具有較大LE 值的情況下，本文設置N= 64.

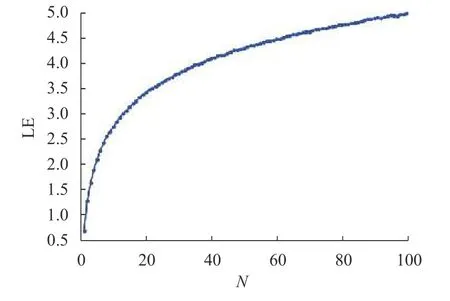
圖1 局部混沌函數PLM 的LEFig. 1 LE of local chaotic function PLM

1.2.2 分叉圖

由式（4）可知，模型的最大LE 與其尺寸無關.為了便于硬件實現，設置R=L= 8. 在兼顧格子之間必要耦合強度且LE 取得較大值的條件下，設置 ε =0.1. 在2DCML 模型中，每個格子的動力學性能相似，所以以格子(4,4)為代表分析模型的分叉情況，如圖2 所示.

圖2 2DCML 模型中格子（4,4）的分叉圖Fig. 2 Bifurcation diagram of lattice (4,4) in 2DCML

在圖2 中，無論 μ 為何值模型都處于混沌狀態，并且隨著 μ 的增加，其分叉行為變得更加復雜，在μ= 4 時其分叉行為最復雜，混沌性能最好. 因此，本文將 μ 設置為4.

1.2.3 遍歷區間

遍歷區間的大小與密碼學中混沌的不可預測性密切相關. 在 μ = 4，N= 64 時，繪制2DCML 模型中格子(4,4)的遍歷區間，如圖3 所示. 從圖3 中可以看出：模型能夠遍歷整個相空間區間(0,1). 這說明2DCML 模型具有良好的遍歷性.

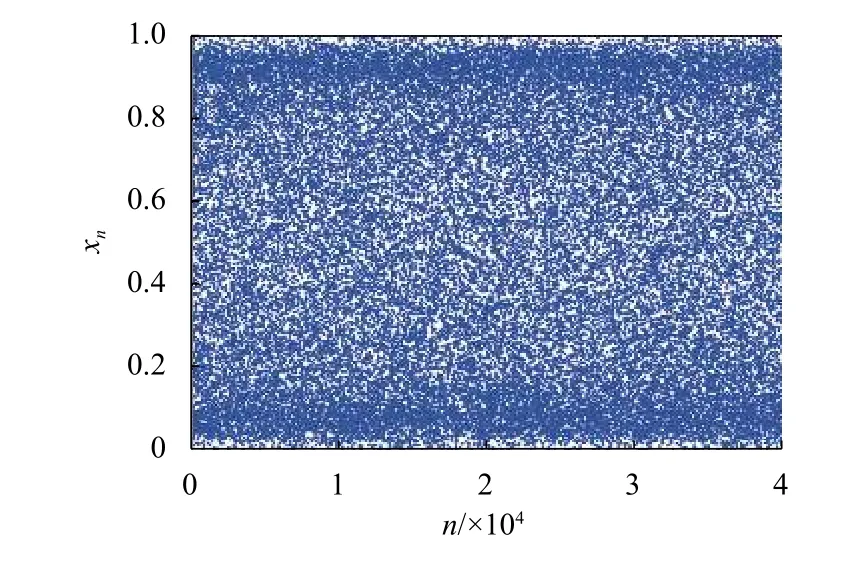
圖3 2DCML 模型中格子(4,4)的遍歷圖Fig. 3 Ergodic diagram of lattice (4,4) in 2DCML

1.2.4 概率密度分布

概率密度分布描述了狀態值在相空間中的分布情況. 2DCML 模型的狀態值的概率密度分布如圖4所示. 從圖4 中可以看出：該模型狀態值的概率密度分布是不均勻的. 這種現象為統計攻擊提供了便利，容易產生安全問題，因此不利于該模型在信息安全中的應用.

圖4 2DCML 的概率密度分布Fig. 4 Probability density distribution of 2DCML

1.3 均勻化處理

為了在2DCML 模型中獲得更均勻的狀態值分布，本文設計了一個基于暫態數據的轉換函數T. 假設計算機中一個定點數的精度是2A位（A為定點數精度的一半），對于任意定點數u∈(0,1)，其二進制格式可以表示為

式中：uk∈{0,1}，k= 1，2，···，2A表示小數點后面的第k位.

變換函數T的定義如下：

在函數T中，所有的變量都是長度為2A的定點數. 對于乘積t，只保留了小數點后的前2A位，舍棄的后2A位為暫態數據. 文獻[20]研究表明，暫態數據擁有良好的隨機性質. 因此，通過與暫態數據進行異或操作，輸出結果o具有很好的隨機性. 由于精度有限，函數T在計算機實現過程中不能直接通過將u和v相乘. 但通過大整數之間的乘法規則，即將二進制整數u1u2···u2A和uA+ 1uA+ 2···u2Au1u2···uA的乘法代替定點數乘法u×v，即可得到暫態數據.

1.4 T2DCML 模型的性能分析

以1.2 節中2DCML 模型為基礎，將該模型迭代后產生的狀態值使用暫態函數T進行變換，進而得到新的暫態均勻化的混沌模型，為描述方便將其稱為T2DCML 模型.

在T2DCML 模型中，設置模型中的參數R=L= 8，N= 64. 采用同樣的方法，測試其分叉情況如圖5 所示. 從圖5 中可以看出：無論 μ 取何值，T2DCML都具有復雜的分叉情況. 同時對比圖2，可以看出：T2DCML 模型具有更復雜的分叉行為. 這說明T2DCML模型的混沌性能得到了增強.

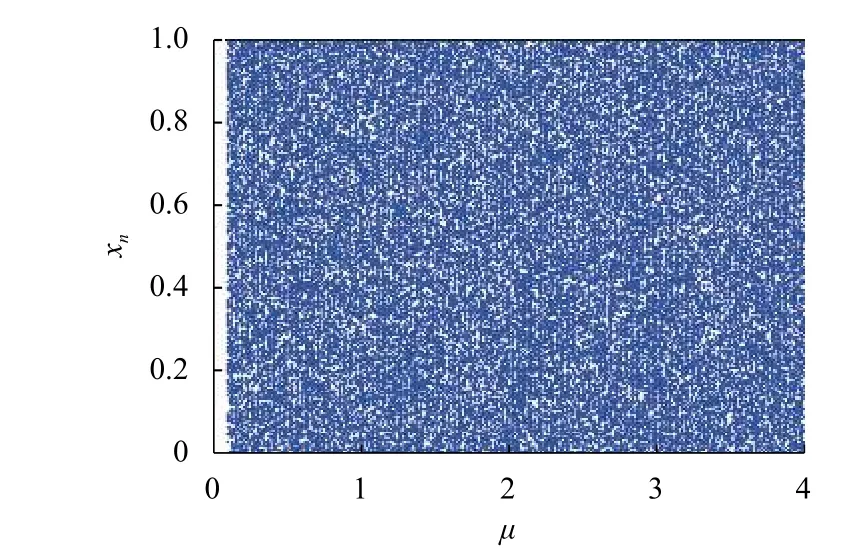
圖5 T2DCML 模型中格子(4,4)的分叉圖Fig. 5 Bifurcation diagram of lattice (4,4) in T2DCML

T2DCML 產生混沌序列的概率密度分布如圖6所示. 與圖4 相比，T2DCML 模型的概率密度已趨于均勻分布. 這表明T2DCML 模型所產生的序列具有良好均勻性，能夠有效滿足相應的安全要求.

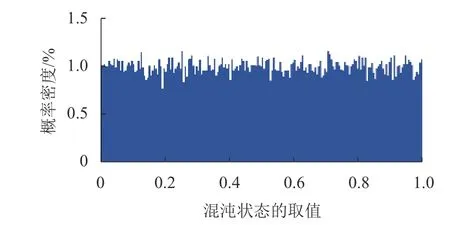
圖6 T2DCML 的概率密度分布Fig. 6 Probability density distribution of T2DCML

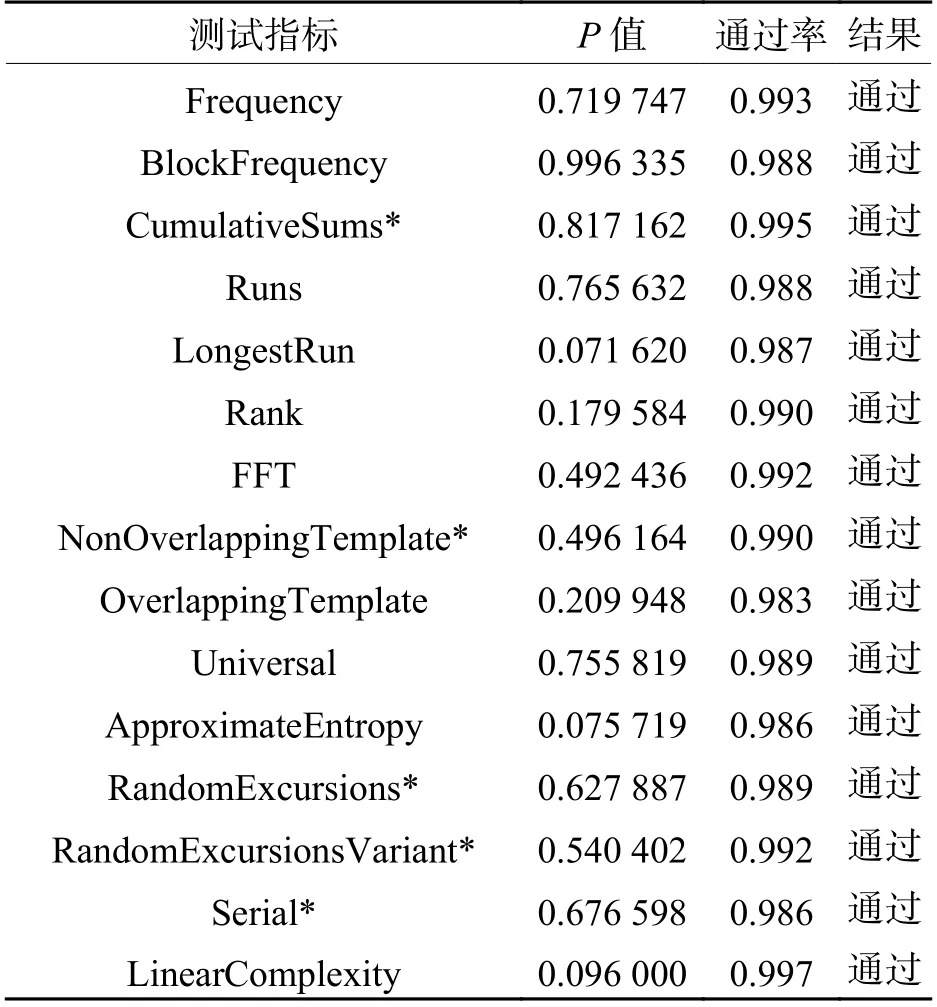
表1 NIST 套件的測試結果Tab. 1 Test results of NIST suites

2 算法設計

2.1 圖像加密算法

本文采用置亂擴散結構作為圖像加密的框架.在該算法中，加密后的像素點不僅取決于其原始位置和值，還取決于其周圍的其他像素點. 在置亂階段，利用T2DCML 模型所產生的序列構造了兩個初等變換矩陣，對像素點矩陣進行置亂. 在擴散階段，從T2DCML 模型狀態值中提取整數序列，對置亂后的像素點矩陣進行擴散，并利用明文反饋調整T2DCML 模型的狀態值，增強加密算法抵抗選擇明文攻擊的能力. 在交替進行多倫置亂與擴散操作后，輸出生成密文圖像. 加密算法的具體步驟如下：

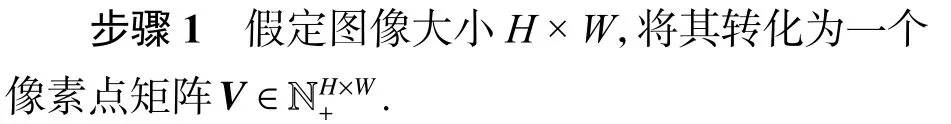
步驟2 假定T2DCML 模型的大小是R×L.輸入PLM 的初始狀態值x0，對PLM 迭代100 次以消除初值x0的影響. 然后，繼續迭代PLM 模型R×L次，獲得每次迭代產生的狀態值序列. 按照從左到右、從上到下的順序賦值給T2DCML 模型，完成初始化，如式（6）所示.

步驟3 構造兩個初等矩陣P和Q，包括以下4 個子步驟：

1） 迭代一次置亂T2DCML 模型并將產生的R×L個狀態值依次存儲到序列p中，繼續迭代該模型直到p存儲了H個浮點數，記作p= {ph}，h= 1，2，···，H.

2） 將p中的元素按照從大到小的順序排序，排序后的序列記作p′.

不難發現，所構造兩個初等矩陣的逆矩陣與轉置矩陣相等，即P′=PT，Q′=QT，這一特性將會用于圖像解密的逆置亂，即V=PTV′QT.

步驟5 將V′按從左到右、從上到下的順序轉換為整數序列I. 另外構造一個T2DCML 模型，其初始狀態與步驟2 中的T2DCML 模型相同. 每迭代一次T2DCML 模型，就從該模型的每個格子中依次提取當前狀態值的前8 比特，得到整數序列Y. 利用序列Y對序列I進行擴散，如式（11）.

式中：Im為序列I中的第m個字節對應的整數值；Ym為序列Y中的第m個字節對應的整數值；C0∈[0,255]為預設的擴散常數.

若序列I中數據尚未被完全處理，則利用明文反饋的形式調整T2DCML 模型的狀態值如下：

調整狀態值后，再次迭代混沌模型并抽取新的狀態值補充到序列Y中. 重復該過程，直至序列I中的所有值被處理完.

步驟6 重復步驟3～5 的置亂擴散操作M次，最終輸出密文圖像. 重復的次數越多，加密的效果越好，同時，需要的時間也越多.

2.2 圖像解密算法

解密算法的過程與加密算法相反，主要步驟相似，此處不再詳述. 需要注意的是，解密所需的所有混沌序列都應該提前生成，以方便與每輪解密所需的序列配對. 式（13）為與式 （11）對應的解密公式.

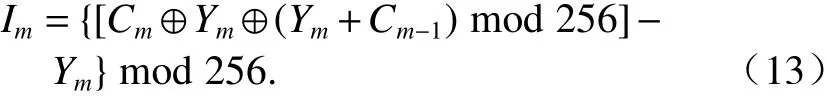
3 算法性能分析

3.1 加解密測試

選取典型的標準圖像Lena、Baboon、Pepper 以及全白（White）和全黑（Black）作為明文圖像，對本文提出的圖像加密算法進行測試，設置加密次數M= 2，結果如圖7 所示. 從圖7 中可以看出：密文圖像很好地隱藏了明文圖像的有用信息，在視覺上有良好的加密效果；解密算法能夠無損地恢復出明文圖像. 測試結果表明，本文算法能夠有效正常工作，滿足通常的圖像加解密需求.

圖7 明文圖像和密文圖像Fig. 7 Plaintext images and ciphertext images

3.2 統計分析

從直方圖分析和相關性分析兩個方面測試了算法的加密效果. 繪制灰度圖像Lena、Baboon、Pepper、White 和Black 的直方圖如圖8 所示. 同時，為了便于對比，在圖8 中還繪制了加密這些圖像后得到的密文圖像的直方圖. 從如圖8 可以看出：加密后的圖像很好地隱藏了明文圖像中的統計信息，使得算法能夠有效地抵御統計攻擊.

圖8 圖像加密前、后的直方圖Fig. 8 Histograms before and after image encryption

相關性分析的具體測試方法是首先從水平、垂直和對角線3 個方向隨機選出1 000 對相鄰的明文像素點和密文像素點，然后計算其相關系數，如式（14）.

式中：cov(x,y)為序列x與序列y的協方差；D(?)為序列的方差.

得到Lena、Baboon、Pepper、White 和Black 圖像在加密前后相鄰像素點之間的相關系數如表2所示：從表2 中可以看出：雖然明文圖像的像素點之間存在明顯的相關性，但是被本文算法加密之后，密文圖像的像素點之間的相關系數非常小，不存在相關關系.

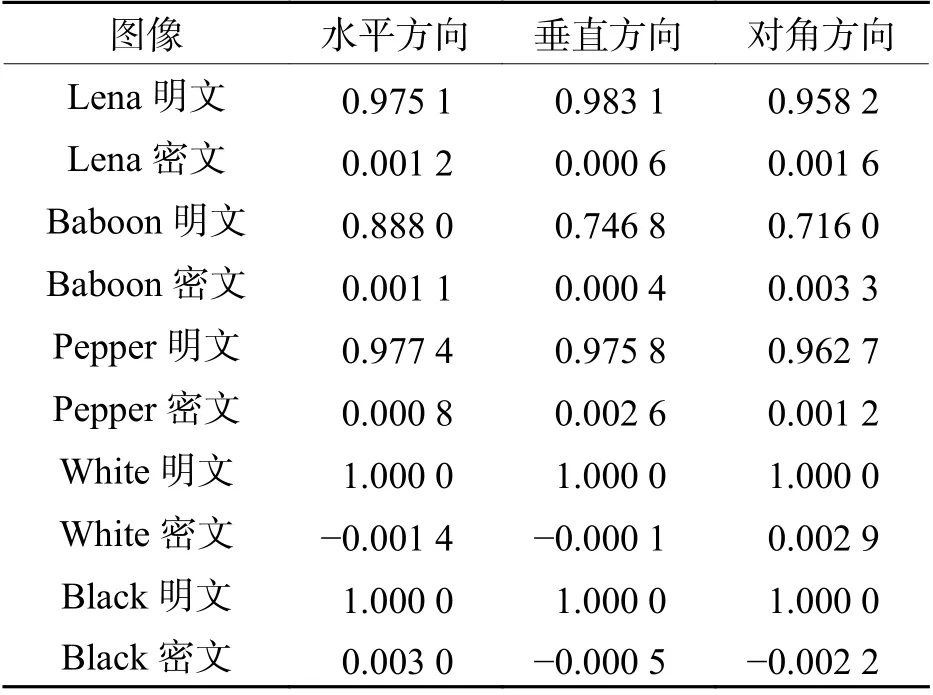
表2 加密前后相鄰像素間的相關系數Tab. 2 Correlation coefficients between adjacent pixels

直方圖分析和相關性分析的結果表明本文提出的圖像加密算法具有良好的抗統計攻擊能力.

3.3 信息熵

信息熵表征圖像中所包含信息的累積和分散，其計算如式（15）.

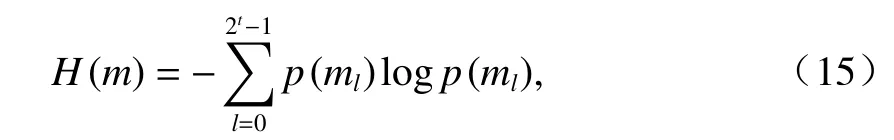
式中：p(ml)為信息值出現的概率；t為自然數.

由于像素點的值使用字節表示，所以其取值范圍為[0,255]，對應的信息熵的理想值為8. 加密后圖像的信息熵越接近理想值，表明圖像中包含的有效信息越少. 表3 列出了使用本文算法加密圖像Lena、Baboon、Pepper、White 和Black 前、后的信息熵.

表3 加密前后圖像的信息熵Tab. 3 Information entropies of images

從表3 中可以看出：無論什么明文圖像，在加密之后，其密文圖像的信息熵都接近理想值. 這說明本文提出的加密算法能夠有效防止密文圖像的信息泄露，可以有效地抵抗基于信息熵的攻擊.

3.4 密鑰分析

3.4.1 密鑰空間

對于加密算法，應該有足夠的密鑰空間（> 2128）來抵抗蠻力攻擊. 在本文算法中，密鑰包括初始狀態值x0∈(0,1)、控制參數 μ∈ (0,4]、耦合強度ε ∈(0,1)和擴散常數C0∈[0,255]. 假設計算機中的浮點數計算精度為10?14， 則算法的秘鑰空間大小為1014× (4 × 1014) × 1014× 28≈ 2150. 根據IEEE 浮點數標準， 64 位雙精度數的精度高于10?14，所以，本文算法的密鑰空間大于2150，能夠滿足抵抗暴力攻擊的要求.

3.4.2 密鑰敏感度

對于密鑰敏感度，進行以下測試.

測試1：將初始狀態值x0變為x0+ 10?15；

測試2：將控制參數 μ 變為 μ ?10?15；

測試3：將耦合強度 ε 變為 ε + 10?15；

測試4：將擴散常數C0變為(C0+ 1) mod 256；

在上述4 種不同的情況下，對圖像采用2 輪加密，比較密鑰變化前后的密文之間的差異. 結果如表4 所示. 從表4 中可以看出：密鑰的微小變化會使密文產生巨大的變化，密文圖像的差異都在99.5%以上. 說明該算法具有良好的密鑰敏感性.

表4 密文圖像的差異Tab. 4 Differences between ciphertext images %

3.5 差分攻擊

在差分攻擊中，攻擊者通常對明文進行輕微的調整，然后比較調整前后產生的密文之間的差異來進行攻擊. 對于圖像加密的差異攻擊，通常使用像素變化率（number of pixel change rate，NPCR）和統一平均變化強度（unified average change intensity，UACI）這兩個指標進行評估，相應的計算如式（16）、（17）.

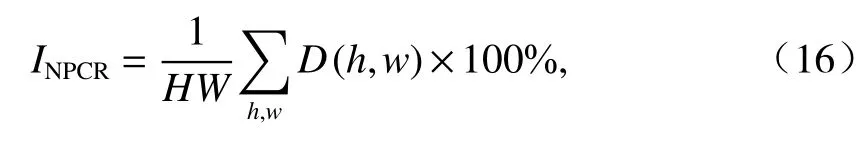
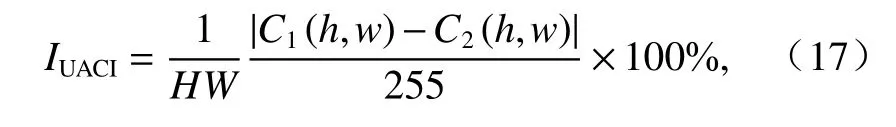
式中：C1、C2為兩個密文圖像，它們對應的明文圖像只有一個像素點的值不同；w= 1,2,···,W；D(h,w)定義為

NPCR 和UACI 理想值分別為99.6%和33.3%.表5 展示了不同圖像在2 輪加密輪加密后的NPCR和UACI. 從表5 中可以看出：NPCR 和UACI 的計算值已經達到各自的理想值. 說明所提出的算法具有有效抵抗差分攻擊的能力.

表5 密文圖像的NPCR 和UACITab. 5 NPCR and UACI of ciphertext images %

3.6 安全性分析

在本文算法中，T2DCML 模型所產生的混沌序列具有至關重要的作用，它驅動著置亂操作和擴散操作的執行. 首先，T2DCML 模型屬于高維混沌系統，具有良好的混沌性能和復雜的動態行為，能夠有效防止攻擊者通過相空間的重構的方式來預測它所產生的混沌序列；其次，T2DCML 模型有效利用了暫態數據特點，保證了數據分布的均勻性，提高了其所產生序列的隨機性，NIST 測試的結果進一步驗證了這一點. 由于T2DCML 產生的序列具有良好的隨機性，因此可以有效保證置亂階段所構造的變換矩陣的隨機性，進而保證了置亂變換的安全.

在擴散階段，本文算法采用明文反饋的方式，對T2DCML 的狀態值進行了調整. 這種處理方式使得擴散階段所使用的偽隨機序列不僅與混沌系統相關，也與加密的圖像相關，從而可以有效防御已知明文攻擊和選擇明文攻擊. NPCR 和UACI 的測試也有效證實了這一點.

此外，本文算法具有足夠大的密鑰空間，能滿足暴力攻擊的要求. 實驗測試的結果反映出由本文算法加密的圖像，其直方圖分布均勻，像素點間沒有相關性，密文圖像的信息熵非常接近理想值8，能夠有效抵抗統計攻擊和信息熵攻擊能力.

3.7 效率分析

在本文算法中，首先需要不斷迭代T2DCML 模型，并從中抽取出相應的狀態值構造變換矩陣，進行置亂操作，然后，再迭代混沌映射產生擴散操作所需要的偽隨機序列. 與2DCML 模型相比，T2DCML 在混沌系統迭代之后還需要進行1 次T變換操作. 在T變換操作中，需要對狀態值進行1 次移位操作，1 次乘法操作和1 次異或操作. 雖然本文算法中引入了T變換操作，但由于該操作增加的計算量僅為少量的幾次基本運算，所以對運算效率的影響很小.因此本文算法的運算效率與已有的基于時空混沌模型的圖像加密算法[15-16]相當. 使用Python 語言實現算法，在CPU 為Intel(R) Core(TM) i3-4005U 的筆記本電腦上測試加密速度，得到加密時間與加密像素點之間的關系如圖9 所示. 從圖9 中可以看出：加密時間與加密圖像的尺寸之間是呈線性變化關系的.這表明本文算法中所采用加密變換能夠很好適應圖像尺寸的變化，能夠滿足在Internet 網中進行圖像加密的效率需求.

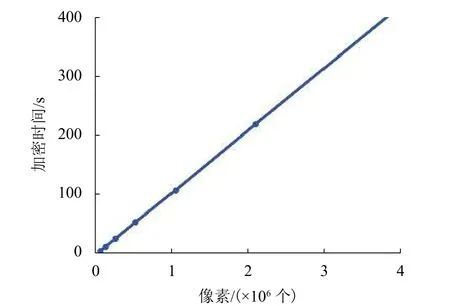
圖9 加密時間與加密像素點數量的關系Fig. 9 Relation between encryption time and number of pixels

同時，T2DCML 模型是一個高維的復雜混沌系統，它能產生具有非常良好加密性能的混沌序列，但是迭代該模型的計算量要高于迭代簡單混沌系統的計算量，因此本文算法的效率要略低于這類圖像加密算法[21]. 此外，由于T2DCML 模型是由多個格子組成，每個格子相對獨立且計算量相當，在未來的工作中可以考慮引入并行處理措施，進一步提高本文算法的效率.

3.8 對比分析

為了進一步說明本文算法的性能，將該算法與同樣基于混沌映射的算法[4-10]比較了512 × 512 的Lena 圖像的性能，結果如表6 所示. 在所有算法中，本文算法的相關系數的平均值更接近0，信息熵的性能也略大，且NPCR 和UACI 均已達到理想值. 說明該算法足夠安全，能夠應用于網絡圖像的安全傳輸.

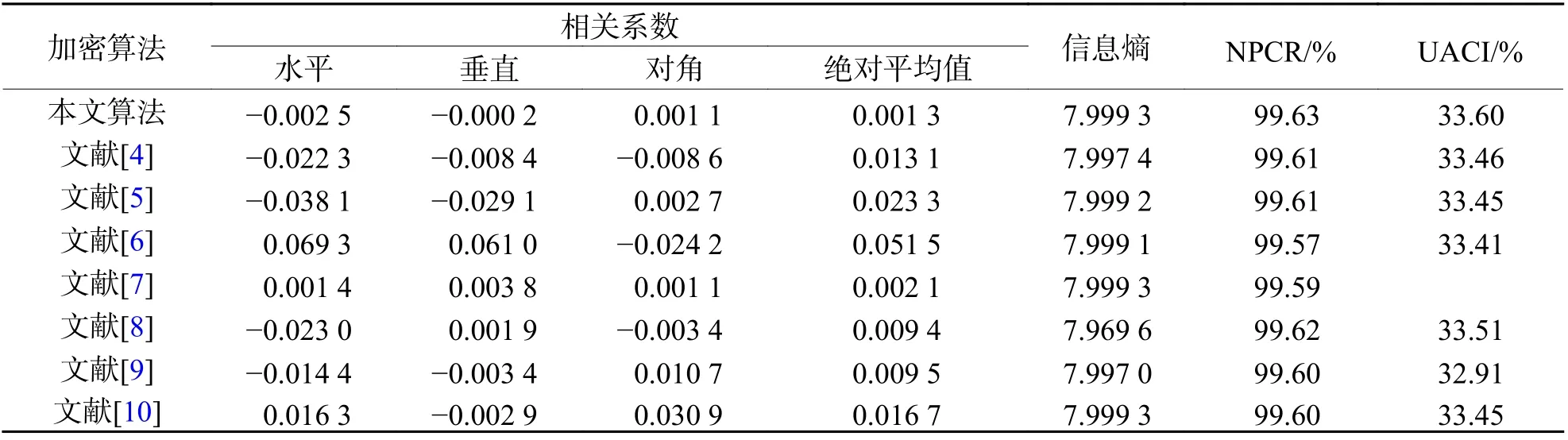
表6 算法性能對比Tab. 6 Comparison of algorithm performance

4 結 論

本文提出了一種基于均勻化時空混沌的圖像加密方案.

1） 提出了一類分段時空混沌系統，以較小的計算代價換來較大的性能提升.

2） 對模型的輸出序列進行暫態變換，使生成的序列服從均勻分布，增強了混沌模型狀態值的不可預測性，保證了混沌序列的高度安全性.

3） 提出一類混沌圖像加密算法，利用矩陣的初等變換簡化圖像置亂階段，彌補了上述兩點對加密方案增加的時間復雜度.

4） 仿真實驗及性能分析表明該算法具有良好的安全性，能夠有效地滿足圖像在網絡中安全傳輸的需求.

致謝：廣西密碼學與信息安全重點實驗室基金（GCIS201908）.