人工智能算法在船舶航線規劃數學建模及求解中的應用

信曉藝

(德州學院 數學與大數據學院，山東 德州 253023)

船舶航線規劃對解決船舶航線安全問題，節約航線損耗來說有重要意義，一旦船舶航線規劃不當，會產生很大的問題，因此想要解決船舶運輸過程的問題，需要設置完備的船舶航線規劃[1]，在規劃船舶航線時，經常使用數學建模及求解的方法，計算出此時航線的最優路徑，避免發生碰撞事故。隨著計算機技術的不斷發展，人工智能、深度學習等現代科學術語頻繁出現在人們生活的各個領域[2]，而人工智能技術也對船舶運輸產生了非常重要的影響，可以利用人工智能技術衍生的人工智能算法，對船舶航線規劃的數學建模進行求解。因此，人工智能技術影響著智能導航的發展。

無人船舶發展的核心技術是船舶航線智能規劃技術，尤其是面臨復雜的海上環境，船舶航線規劃技術研究對無人船舶行駛的作用就更為重要[3]。在實際的海上交通運輸活動中，船舶面臨的海上交通環境十分復雜，船舶航行高度在不斷變化的海域中顯著增加。近期，全球海上交通事故頻發[4]，在必須解決海上交通面臨的各種問題的情況下，如何才能最大限度地減少海上交通事故的發生，最大限度地保護生命財產安全？是一個亟待解決的問題。毫無疑問，智能船舶導航技術和船舶自動化操作是解決當前問題的好方法。在船舶智能導航中，船舶航線的自動規劃是一個非常重要的環節，關系到船舶駕駛的強度和船舶的安全性能，直接影響到人們的生命財產安全。尤其是復雜水域中的船舶航線規劃，對于研究具有重要意義，因此，本文設計了基于人工智能算法的航線規劃建模求解方法。

1 基于人工智能算法的航線規劃建模求解方法設計

1.1 描述船舶航行航線及約束條件

對于現有的航行船只，通過分析歷史數據，可以預測船舶在運輸過程中的航線、貨量和作業水平，基于技術可行性建立船舶航線規劃的目標函數[5]。在本研究中，在提出路徑規劃目標函數之前，首先需要假設船舶運行函數，確定航線規劃的研究周期，在航線規劃過程中設置可用船型和可用航線，設置的航線多為傳統的多港口直達航線[6]。根據原航線的歷史數據，在規劃過程中需要預測起始點和目的地之間的貨運需求和運輸成本。在航線規劃的研究周期中，根據各類船舶的最大航速進行分析，確定航線往返次數。在設計過程中，既保證了運營成本的穩定性，又控制了航運成本，使其不受航次貨量變化的影響。

在建立數學模型之前，需要將船舶在各種狀況下的航行狀態記錄下來，因此需要將船舶行駛的環境逐一記錄，本文設計的求解方法是在高線法和網絡法的基礎上建立的網絡優化高線法，S代表船舶在出發時所處的位置，G代表船舶航行結束后停靠的位置，經過研究，發現船舶在航行時會途經多個點，將這些點分別設為r1,r2,…,rN-1，基于此，設此時的船舶航行線路如公式(1)所示。

Rk={S,r1,r2,…,rN-1,G}

(1)

根據公式(1)中描述的航行線路，進行初次運行，發現此時運行存在一定的問題，因此需要對船舶航行中的某些條件進行約束。經過研究發現，船舶的約束條件有幾種，第一種，船舶的最短航線，用lmin表示；第二種，船舶的最長航線，用lmax表示；第三種，船舶的最大航行節點，根據上述三個約束條件，本文設計了約束集合，如式(2)所示。

(2)

公式(2)中，li代表船舶的規劃航線，根據公式(2)即可求出船舶航線的綜合約束范圍。

1.2 建立船舶航線規劃數學模型

根據上文設置的船舶航行線路，帶入船舶綜合約束范圍，即可建立此時航線的數學模型，如式(3)所示。

(3)

公式(3)中，fk代表此時建立的航線規劃數學模型，ω1、ω2均代表權重值，fTAi則代表此時的威脅指標。

經過研究發現，船舶在航行過程中還會受到某些外界因素干擾，例如航行時遇見水流狀態改變或水中有障礙物等，都會影響船舶的最優航線。基于此將整個船舶運行中的威脅指標設置為各個威脅因子的和[7]，可以將此時船舶的航行路徑規劃成三個部分，從而降低航行時由于外界干擾帶來的威脅，計算此時每一個部分的威脅因子數值，并將其求和，得到此時的威脅指標值如式(4)所示。

(4)

根據公式(4)可以求出此時的威脅指標值，帶入到船舶航線規劃的數學模型中，即可求解出人工智能算法求解的基本參數。

1.3 基于人工智能算法對數學模型求解

人工智能算法與傳統的魚群算法和蟻群算法不同，其收斂性和穩定性都比較好，因此利用上文中設計的公式(1)-(4)，根據人工智能算法的最優解求解方式，進行改進，在算法中加入了變異概率和自適應交叉概率，改進后基于人工智能算法設計的交叉概率和變異概率Pm如公式(5)、公式(6)所示。

(5)

(6)

公式(5)、(6)中，Pc1、Pc2代表此時第一次迭代和第二次迭代的交叉率，f′代表適應值，favg代表適應初始值，fmax代表適應最大值，Pm1、Pm2代表第一次和第二次變異產生值，f代表標準適應值。

根據此時的求解公式進行求解后，發現此時缺乏規劃穩定編碼，因此需要設置此時船舶航線的編碼來進行后續的求解，將第i個個體的編碼序列設置為xi1,xi2,…,xim，設置此時船舶航線中的航行節點為r，則此時的編碼位與個體值呈現一一對應的狀態。將個體編碼值代入到交叉概率和變異概率的求解公式中，可以得出此時船舶的交叉概率和變異概率[8]，即可進行后續航線的規劃。

航線的規劃由幾個步驟組成，第一步，建立此時符合航線狀態的參數，設置此時的迭代次數，利用此時的迭代次數進行航行規劃；第二步，根據迭代的參數，建立船舶航行的數學模型設計遺傳算法的適應度函數；第三步是生成初始計劃，每個個體代表一個可行的船舶航線規劃計劃；第四步，根據適應度函數計算個體適應度值[9]，并根據計算結果評估可行的航線規劃方法的優劣；第五步，根據評價結果，選出進入下一代的優秀個體；第六步，選擇一些個體進行交叉和異變，并選擇更好的個體進入下一代種群；第七步，將對數進行比較。如果超過最大值，則停止求解，輸出最優的方案，否則返回第四步。

根據航線的規劃步驟，設計此時航線規劃的數學模型求解函數，如式(7)所示。

(7)

使用此函數，結合人工智能算法改進的交叉概率和變異概率，可得到此次研究中設定目標函數的最優解，如式(8)所示。

(8)

由公式(8)可得，ES為此時航線規劃數學建模的解。

2 仿真測試

采用仿真實驗的方式對文中設計算法與目前使用中算法的計算效果展開分析。在此次實驗過程中，選定某海洋環境地圖對實驗算法進行對比實驗。在此實驗環境中，根據以往計算過程，將慣性權值取值設定為2.0。

2.1 測試場景及準備

為了檢測本文設計的基于人工智能算法的求解方法的有效性，需要進行測試，首先就是進行測試場景準備，為了凸顯人工智能算法的求解效果，需要劃分測試的區域，本文將航線劃分為1500km×1500km，規定航線的起始點和目的地，計算此時的航線威脅指標，將計算的值輸出到規劃表格中，選用指定數量的種群進行迭代次數計算，在C語言環境下進行測試，具體仿真海洋地圖如圖1所示。

圖1 仿真海洋地圖

如圖1所示，在實驗環境中，Q表示路線規劃的起始點，P表示路線的結束點，圖中的黑色方塊表示海洋環境中的靜態障礙物，為了求解三種算法的迭代次數繪制此時三種算法求解后的路線規劃圖，如圖2所示。

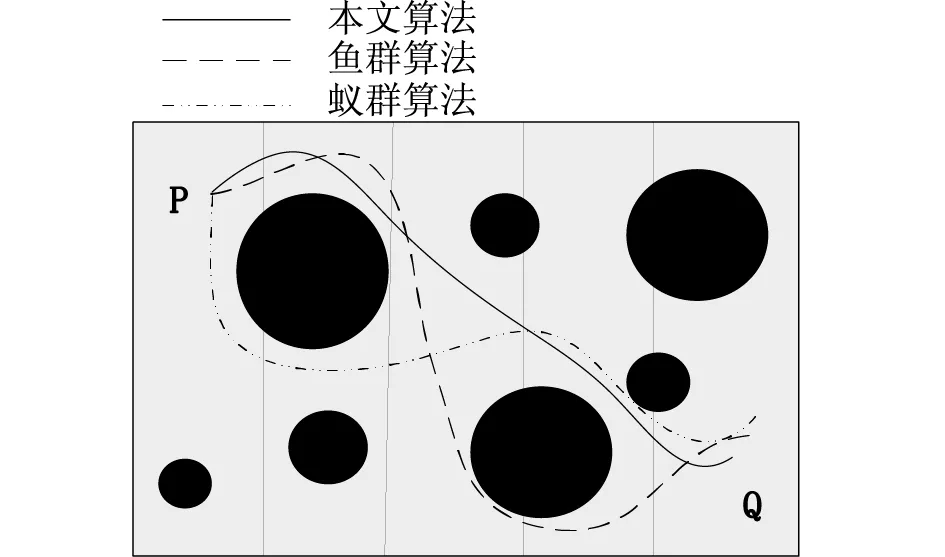
圖2 不同算法路線規劃圖

根據圖2的路線規劃圖，仿真軟件輸出路徑長度，即魚群算法的最優路徑為1800km，蟻群算法的最優路徑為1750km，本文設計算法的最優路徑為1700km。由此可見，本文算法規劃的路徑最短，具有較為優越的性能。

2.2 測試結果與分析

為了檢測設計的人工智能算法的規劃效果，根據上文測試準備中的最優路徑，選擇魚群算法、蟻群算法和本文設計的基于人工智能算法對數學模型分別進行求解，統計幾種方法的迭代次數，測試結果如表1所示。

表1 測試結果

由表1的測試結果可知，本文設計方法的迭代次數低于魚群算法和蟻群算法的迭代次數，可以降低求解時間，提高求解效率，因此本文設計算法的求解性能更佳。

為進一步驗證本文算法的優越性，將三種算法進行求解，重復5次，統計耗時結果并進行對比，得到不同算法的平均耗時結果如圖3所示。

圖3 不同算法的平均耗時

分析圖3可知，文本算法的平均耗時為3.62s，而魚群算法和蟻群算法的平均耗時為8.56s和8.5s。本文算法可以大大減少計算冗余度，進而降低了計算的耗時。

3 結論

綜上所述，規劃最優的船舶航行路線對提高船舶運行安全性，減少船舶危險性來說有重要意義，也可以提高船舶航線規劃水平，因此本文設計了基于人工智能算法的航線模型求解方法，實驗表明，本文設計的方法迭代次數少，能有效降低求解時間，提升求解效率，有一定的參考價值。