基于粒子群極值Kriging模型的壓氣機葉盤時變可靠性分析

王遠卓, 韓治國, 楊子煜, 路成, 薛小鋒

1.北京航空航天大學 宇航學院, 北京100191; 2.西北工業大學 航天學院, 陜西 西安710072;3.復旦大學 航空航天系, 上海200433; 4.西北工業大學 航空學院, 陜西 西安710072

低壓壓氣機轉子系統對于航空發動機的正常運轉起到尤為重要的作用，其功用是通過壓縮氣體來提升整個系統的熱力循環效率。低壓壓氣機葉盤工作環境嚴苛，承受著高壓、高轉速等交變載荷作用[1]，一旦發生功能失常，將對航空發動機產生二次損傷，造成災難性后果。因此，為了保障航空發動機系統安全運行，有必要開展低壓壓氣機葉盤時變可靠性分析。

近年來，國內外學者基于蒙特卡洛(Monte Carlo,MC)模擬與近似解析法開展了許多研究，對航空發動機壓氣機葉盤進行了可靠性分析。趙洪利等[2]基于MC模擬，給出了用于評估航空發動機發生故障可能性的風險預測方法；Narayanan等[3]提出了基于MC模擬的航空發動機結構疲勞壽命估算方法；楊周等[4]根據模擬的隨機參數與隨機響應的關系，通過一次二階矩法對發動機進行可靠性分析；張飛[5]對一次二階矩法在均值點進行線性化展開的基礎上進行改進，提出了通過在驗算點進行線性化對發動機葉盤進行可靠性分析的改進一次二階矩方法；白冰等[6]針對強非線性問題高精度可靠性求解困難的問題，依據二次二階矩建立了可靠度指標分析方法。上述研究工作為航空發動機壓氣機葉盤結構可靠性分析提供了思路，但MC模擬需要通過大規模計算來實現可靠性分析，耗時較長且不能高效完成具有動態時變特性的可靠性評估；近似解析法適用于功能函數已知的可靠性分析，對于壓氣機葉盤這類復雜結構可靠性分析，其功能函數通常是未知的。為合理規避MC模擬與近似解析法存在的缺點，許多專家學者通過構建代理模型進行結構可靠性分析。高陽等[7]提出了徑向基函數神經網絡模型，對高壓渦輪盤疲勞可靠性分析進行了研究；劉佳奇等[8]基于智能神經網絡提出了一種航空發動機運行狀態下的時變安全性分析方法；馬小駿等[9]基于最小二乘支持向量機算法對航空發動機壽命進行了分析。上述代理模型雖然一定程度上提高了可靠性分析的效率，但是對于具有時變特性的可靠性分析問題，需要建立大量的代理模型獲取結構可靠性指標，其分析流程過于復雜。因此，部分學者將極值思想引入代理模型來簡化可靠性計算的負擔。Zhang等[10-11]為有效地進行渦輪葉盤疲勞可靠性及中心齒輪可靠性分析，基于響應面方法，借鑒極值思想提出了多重極值響應面策略； Bai等[12]針對航空發動機葉盤的非確定性因素提出了一種基于動態子結構的極值響應面法。然而，上述方法在構建功能函數過程中采用的是基于二次多項式的形式，其可靠性分析精度與工程需求存在偏差。

為了解決上述問題，本文基于Kriging模型，結合極值思想和粒子群算法(PSO)，提出了粒子群極值Kriging模型方法(PSOEKM)，用以實現航空發動機低壓壓氣機葉盤時變可靠性分析。其中，極值思想用以簡化動態分析流程，以輸出響應的極值代替整個時變過程；PSO算法用以替代梯度下降，實現Kriging模型超參數尋優；Kriging模型用于建立輸出響應與輸入參數之間關系，進而實現可靠性分析。此外，通過多種方法對比驗證了本文研究方法的有效性與可行性。

1 粒子群極值Kriging模型

1.1 分析流程

為了合理高效實現航空發動機低壓壓氣機葉盤時變可靠性分析，將極值思想和PSO算法引入Kriging模型，提出PSOEKM方法，其原理為：結合極值思想處理壓氣機葉盤輸出響應的時變過程，運用輸出響應極值將動態分析轉化為瞬態分析；采用PSO算法實現目標函數求解，獲取Kriging模型的超參數；利用Kriging模型描述輸出響應與輸入參數之間的關系，構建功能函數并實現時變可靠性分析。基于PSOEKM方法的航空發動機低壓壓氣機葉盤時變可靠性分析流程如圖1所示。

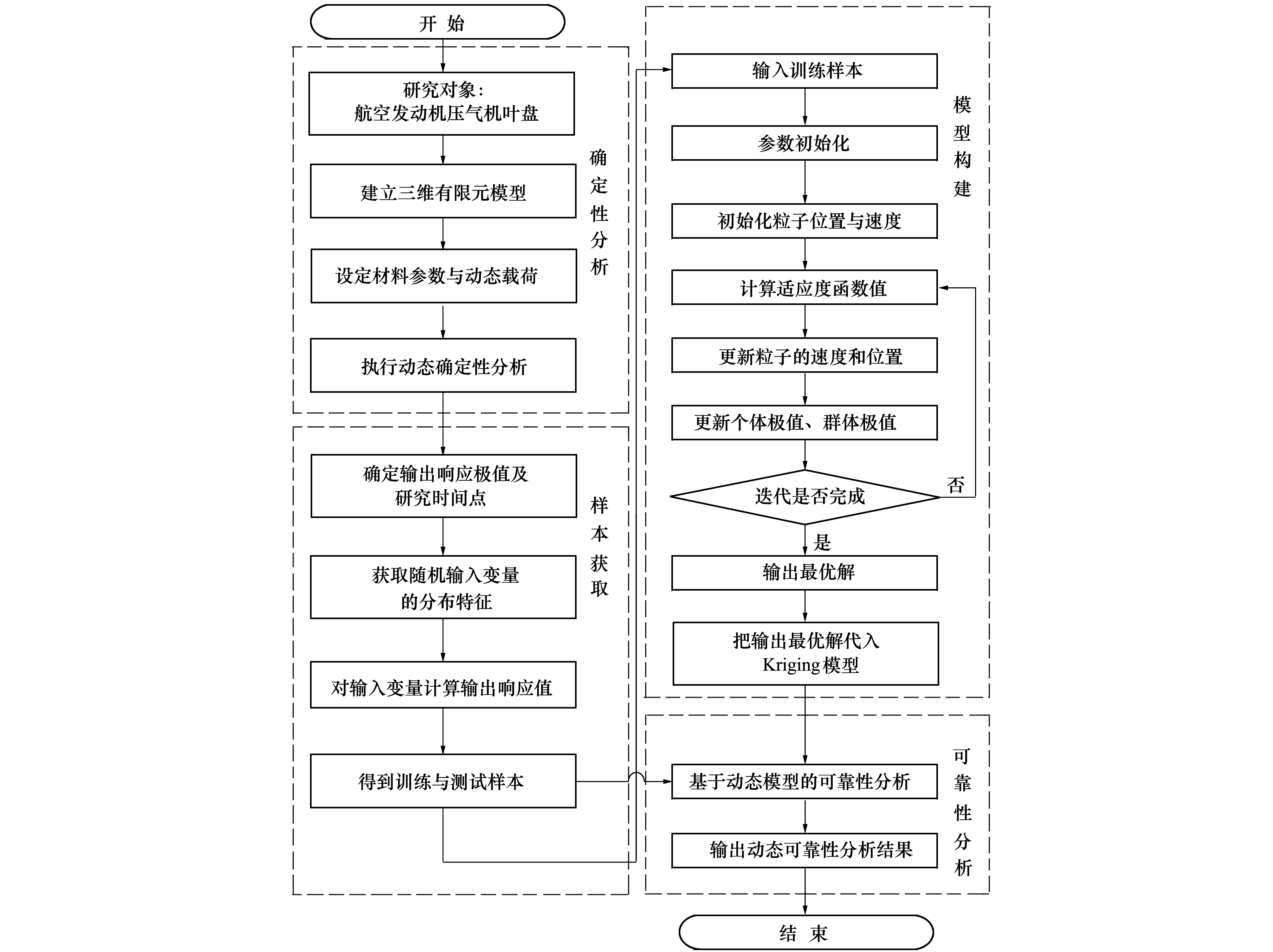
圖1 基于PSOEKM方法的航空發動機低壓壓氣機葉盤時變可靠性分析流程

由圖1可知，基于PSOEKM方法的壓氣機葉盤動態時變可靠性分析包括確定性分析、樣本獲取、模型構建、時變可靠性分析4個部分。具體分析流程如下：

1) 構建航空發動機低壓壓氣機葉盤三維有限元模型，設置材料參數、邊界條件與動態載荷；執行動態確定性分析；獲取輸出響應隨時間變化的規律并結合極值思想確定輸出響應極值與研究時刻點。

2) 基于輸入變量隨機分布特征，獲取足夠的輸入樣本，通過確定性分析計算各輸入樣本對應的輸出響應值；確定用以建模的訓練樣本和用以模型驗證的測試樣本。

3) 結合訓練樣本，運用PSO算法實現模型超參數尋優，并求解PSOEKM的模型系數，構建壓氣機葉盤輸出響應與輸入參數之間的關系模型。其中，基于PSO算法的模型超參數求解步驟為：參數初始化，適應度函數值計算，更新粒子的位置與速度、個體極值與群體極值，完成迭代獲取模型超參數。

4) 在建立的壓氣機葉盤輸出響應模型基礎上，構建其極限狀態函數，采用MC方法進行大量模擬實現壓氣機葉盤時變可靠性分析并輸出結果。

1.2 數學模型

參考Kriging模型,PSOEKM模型y(x)可描述為[13]

y(x)=GT(x)α+z(x)

(1)

式中:y(x)為輸出響應值;α為待定系數向量;z(x)為誤差修正函數;G(x)為基函數矩陣。

與傳統的響應面法相比,Kriging模型的優勢主要體現在誤差修正項z(x),該項的引入可進一步提升了模型變量之間的關聯程度,進而提升了代理模型的精度。通常,誤差修正函數z(x)服從均值為0、方差為σ2的正態分布[14],即

(2)

式中:E為函數均值;var為函數方差;cov為函數的協方差;R為相關函數矩陣,p,q=1, 2, …,m;m為訓練樣本的數量;xp,xq為第p和q個訓練樣本。

xp與xq的相關函數為

(3)

式中:i=1, 2, …,n,n為訓練樣本的維度;θi為第i個模型的超參數。

相關函數常用的形式有指數型、高斯型及線性型等,本文選取高斯型函數作為相關函數的形式,原因在于該形式函數具有較好的擬合性能[15],高斯型相關函數(3)式可表達為

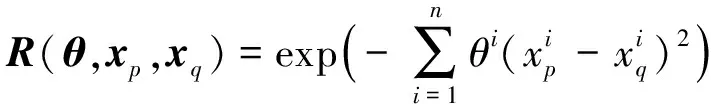
(4)

因此,基于樣本的相關函數矩陣R為

R=

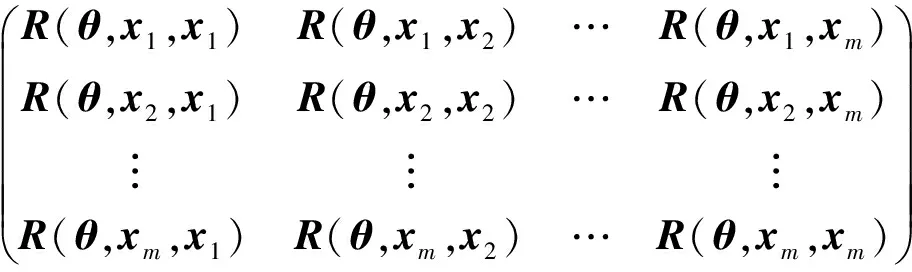
(5)

進而,模型中的待定系數向量α可由(6)式確定

α=(GT(x)R-1G(x))-1GT(x)R-1Ytrain

(6)

式中,Ytrain為訓練樣本的輸出向量。

則誤差修正函數為

z(x)=rT(x)R-1(Y-GTα)

(7)

式中,rT(x)表示單個樣本與所有樣本相關性大小。

rT=[(R(θ,x,x1)R(θ,x,x2…R(θ,x,xm)]。

依據最小二乘理論,模型誤差的方差估計值為

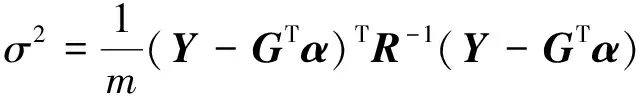
(8)

模型超參數傳統上采用梯度下降法,通過最大化適應度函數進行求解獲取。然而,對于涉及多變量參數高非線性問題,梯度下降策略尋優效率下降,甚至無法得到全局最優解。因此,本文將最大化問題轉化為最小化問題[16]

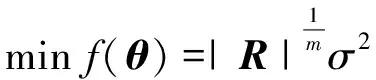
(9)

式中,f(θ)為適應度函數。

為了實現最小化問題求解,采用粒子群算法通過求解(9)式實現模型超參數θ的尋優。粒子群算法通過粒子的隨機性、記憶性、不確定性,改善了基于梯度下降模型參數尋優容易陷入局部最優的問題。相比遺傳算法,PSO算法在更新過程中實時追蹤當前最優粒子,故收斂速度較快[17],可以較好、較快地滿足時變條件下的可靠性分析。粒子群算法粒子的速度和位置更新如(10)式所示

(10)

式中:k為迭代次數;v(k)為當前粒子速度;x(k)為當前粒子位置;c1和c2為學習因子;β為隨機產生的隨機數;xpbest為個體最優值;xgbest為全局最優值。

基于上述分析,結合訓練樣本運用粒子群算法可實現模型超參數尋優,進而結合最小二乘法實現模型系數求解,建立PSOEKM模型(功能函數)。

1.3 時變可靠性分析

基于所構建的功能函數,結合分析目標的許用值,可建立發動機壓氣機葉盤徑向變形的極限狀態函數,其可表達為[18]

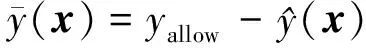
(11)

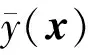
在此基礎上,運用MC法對極限狀態函數進行大量抽樣,利用概率統計分析實現時變可靠性分析,其原理實質是借鑒伯努利大數定律,即

(12)

式中:nB為n次試驗下事件B出現的次數;P為事件B出現的概率;ε為任意很小的正數。

根據(12)式,當試驗次數n趨近于無限大時,n次試驗中滿足可靠性閾值要求的次數將收斂到實際的可靠度,則可靠度計算原理為

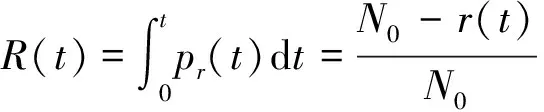
(13)

式中:R(t)為可靠度函數;pr(t)為可靠密度函數;r(t)為0～t時間段內累積的故障數;N0為t=0時規定條件下進行工作的產品數。

2 算例分析

2.1 動態確定性分析

壓氣機工作環境復雜,葉盤作為壓氣機重要的部件之一,其可靠性直接關乎航空發動機整個系統的安全性。選取某型航空發動機低壓壓氣機葉盤作為研究對象,考慮流體載荷和結構載荷的作用,對其徑向變形進行動態可靠性分析。為了實現低壓壓氣機葉盤徑向變形動態可靠性分析,首先建立研究對象的三維模型(如圖2所示),結合構建的三維模型,進而生成低壓壓氣機葉盤的有限元模型(如圖3所示),航空發動機低壓壓氣機葉盤由四面體單元組成,包括150 837個節點和89 424個單元。

圖2 低壓壓氣機葉盤三維模型

圖3 低壓壓氣機葉盤有限元模型

選取1Cr11Ni2W2MoV作為低壓壓氣機葉盤材料,其密度為7.8×103kg/m3、泊松比為0.3、彈性模量為2.06×1011Pa。此外,考慮進口流速、出口壓力、密度和轉速等作用,其中進口流速為124 m/s,出口壓力為5.07×105Pa,以及轉速為1 168 rad/s。需要說明的是:轉速是隨時間變化的,其變化特性參考文獻[16]確定。在有限元模型和載荷參數設置的基礎上,結合有限元法和有限元體積法對壓氣機葉盤徑向變形進行動態確定性分析。在動態確定性分析過程中,分別針對流場和結構場進行設置:在流場中設置進口流速和出口壓力載荷;在結構場中,設置材料參數、轉速。最后對低壓壓氣機葉盤設置圓柱支撐約束。基于確定性分析得到低壓壓氣機葉盤徑向變形隨時間變化曲線如圖4所示。

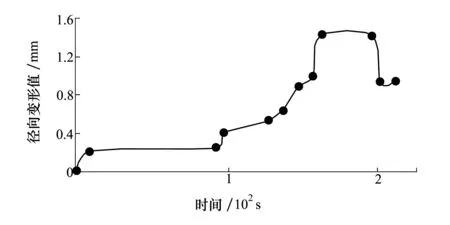
圖4 低壓壓氣機葉盤徑向變形隨時間的變化曲線

由圖4可知,低壓壓氣機葉盤徑向變形的最大值出現在分析時域[165 s, 200 s],任意選取其中某一時刻作為研究時刻點,本文選取t=172 s,則此時的徑向變形分布云圖如圖5所示。由圖5可以看出,低壓壓氣機葉盤徑向變形的最大位置位于葉尖尖端,同時將該部位作為時變可靠性分析研究的部位。

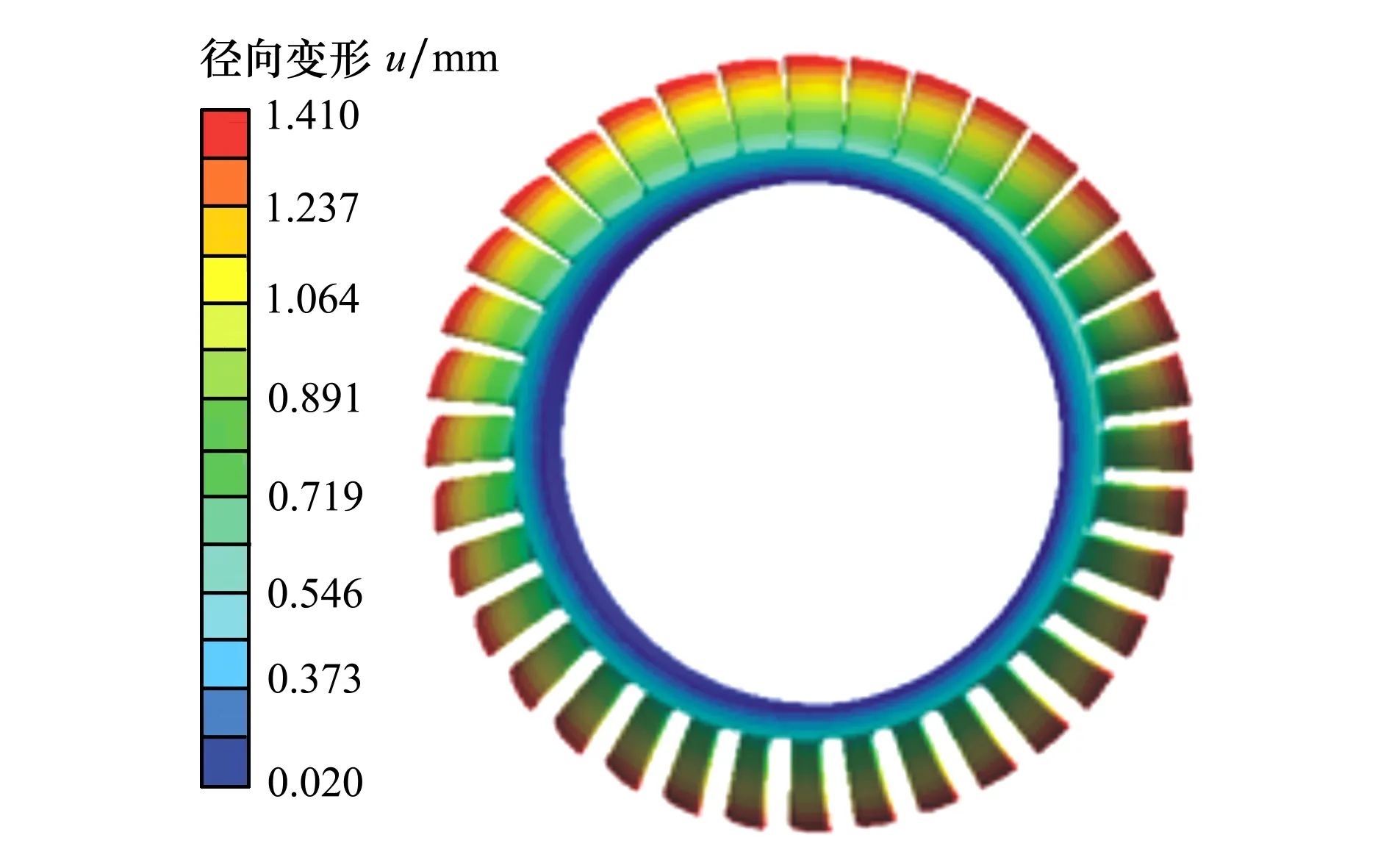
圖5 低壓壓氣機葉盤徑向變形分布云圖

2.2 樣本獲取

基于低壓壓氣機葉盤徑向變形動態確定性分析,結合其最大值出現的時刻和位置,選取進口流速v、出口壓力pout、密度ρ和轉速w作為隨機輸入變量,假設這些變量參數均服從正態分布且相互獨立,其數值分布特征如表1所示[19-20]。

依據表1輸入變量的隨機分布特征,運用拉丁超立方抽樣獲取隨機輸入變量的樣本,并結合多次動態確定性分析計算輸入樣本對應的輸出響應極值(最大徑向變形),進而形成含有輸入變量和輸出響應的樣本。其中,隨機選取一部分樣本作為訓練樣本,用以構建低壓壓氣機葉盤徑向變形的PSOEKM模型(功能函數);剩余的樣本用以驗證PSOEKM模型的精度。

表1 輸入變量的隨機分布特征

2.3 模型構建

基于動態確定性分析獲取的訓練樣本,結合1.2節數學模型構建原理,運用粒子群算法實現PSOEKM模型超參數尋優。其中,粒子群算法尋優的初始化條件設置參數為:學習因子c1=0.56,c2=1.95、最大迭代次數為25、種群規模為20、進化速度范圍為[-13,13]、進化位置范圍為[0.1,20]。基于粒子群算法的適應度函數進化曲線如圖6所示。

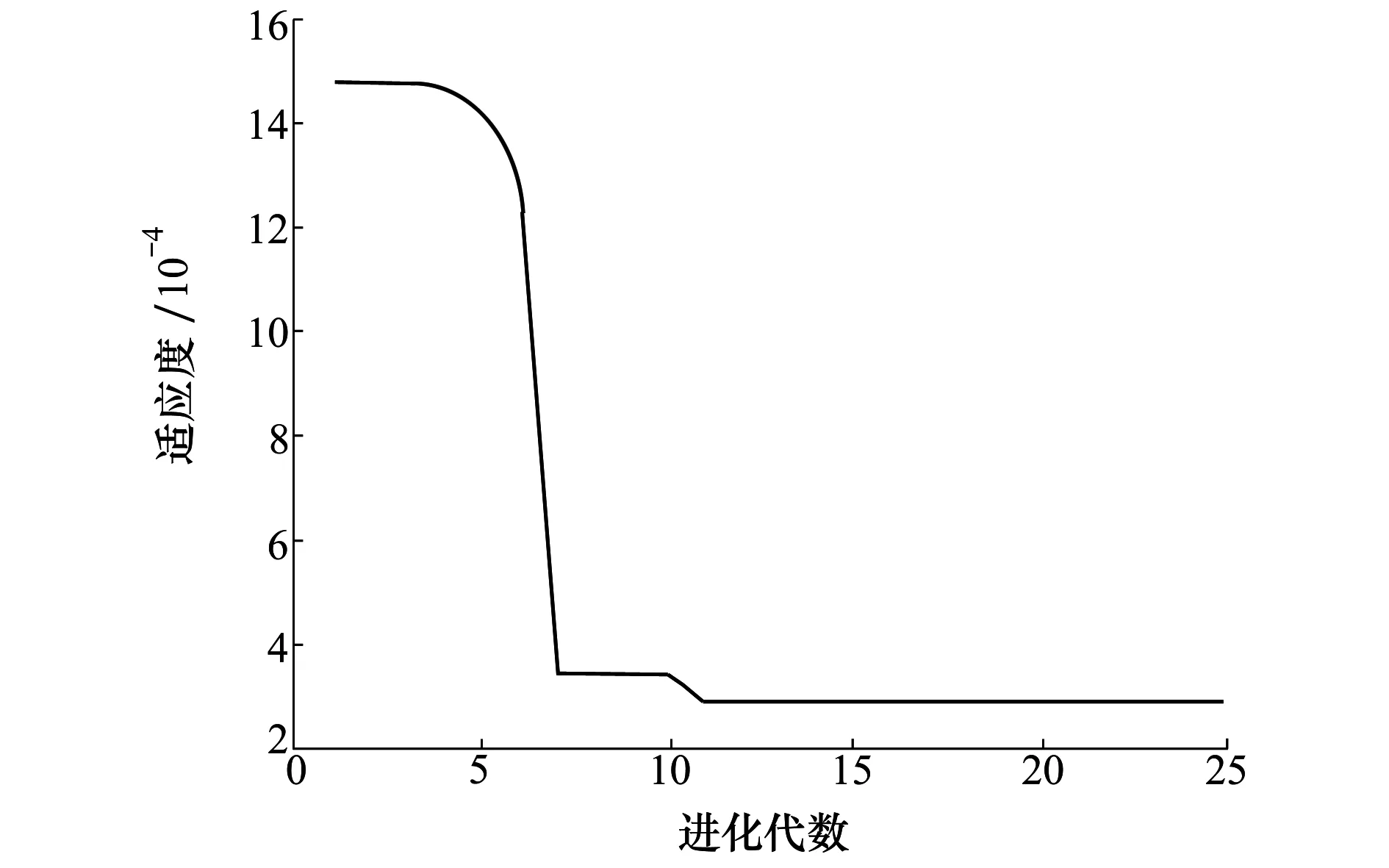
圖6 基于粒子群算法的適應度函數進化曲線

從圖6可以看出,整個粒子適應度函數收斂的過程中,開始收斂速度較快,隨著迭代次數的增加,收斂速度變慢直至穩定。群體粒子適應度通過7次迭代基本收斂,在第12次迭代時目標值達到最小,穩態值為2.9×10-4。此時,PSOEKM模型超參數θ=[0.716,13.500,0.521,0.223]。

在得到模型超參數的基礎上,為構建低壓壓氣機葉盤徑向變形的功能函數,采用最小二乘法實現PSOEKM模型相關函數矩陣R與待定系數α向量的求解

(14)

2.4 可靠性分析

基于建立的功能函數,結合低壓壓氣機葉盤徑向變形的許用值,其極限狀態函數根據(11)式可表達為

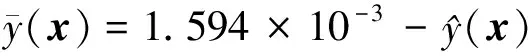
(15)

利用MC法對(15)式進行10 000次仿真抽樣,則低壓壓氣機葉盤徑向變形的仿真歷史與分布直方圖分別如圖7～8所示。由圖7和圖8可知,低壓壓氣機葉盤徑向變形服從正態分布。當低壓壓氣機葉盤徑向變形許用值為1.594×10-3m(該值基于3σ原則確定)時[16],可靠度為99.76%,滿足工程需求。

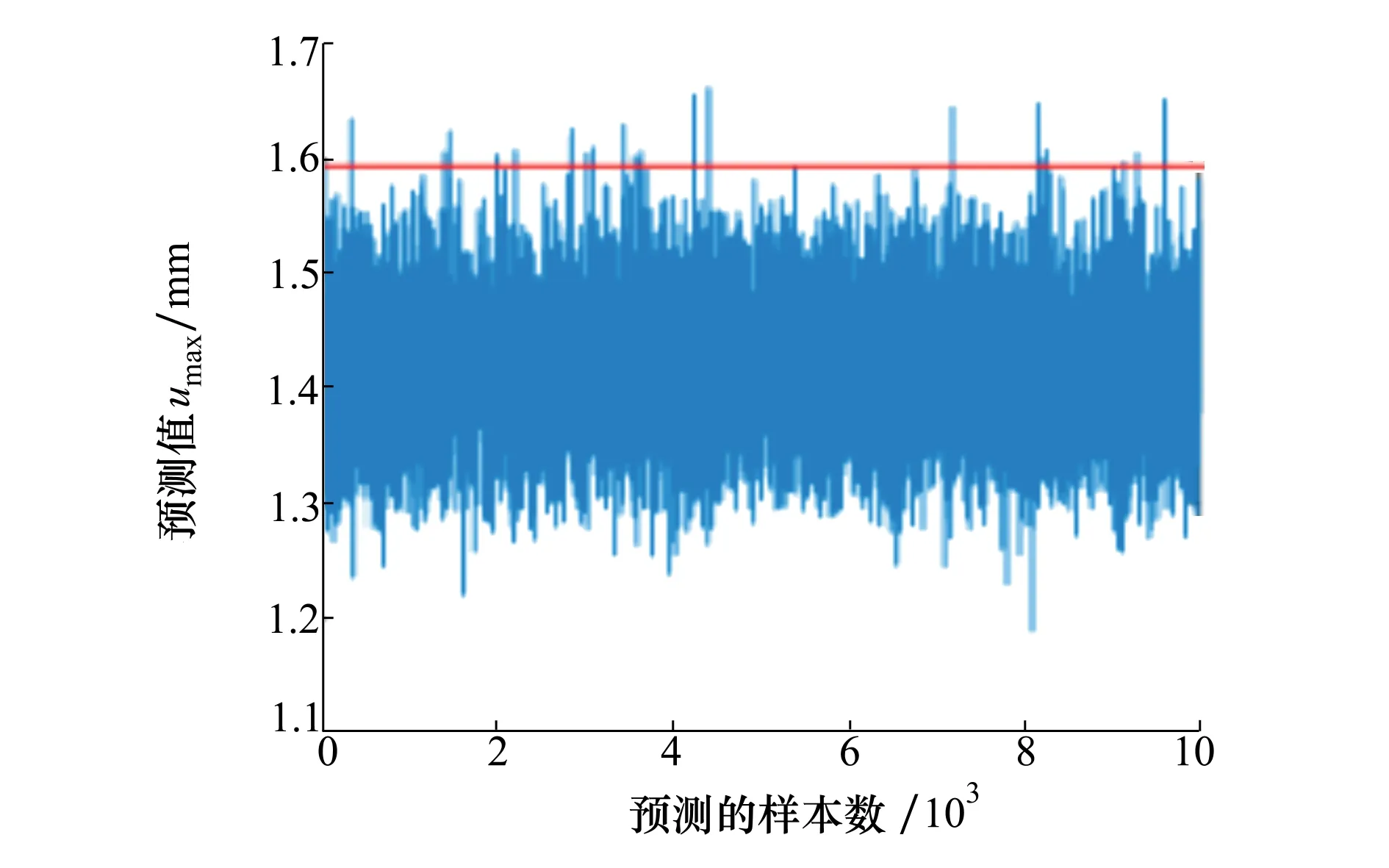
圖7 低壓壓氣機葉盤徑向變形仿真歷史

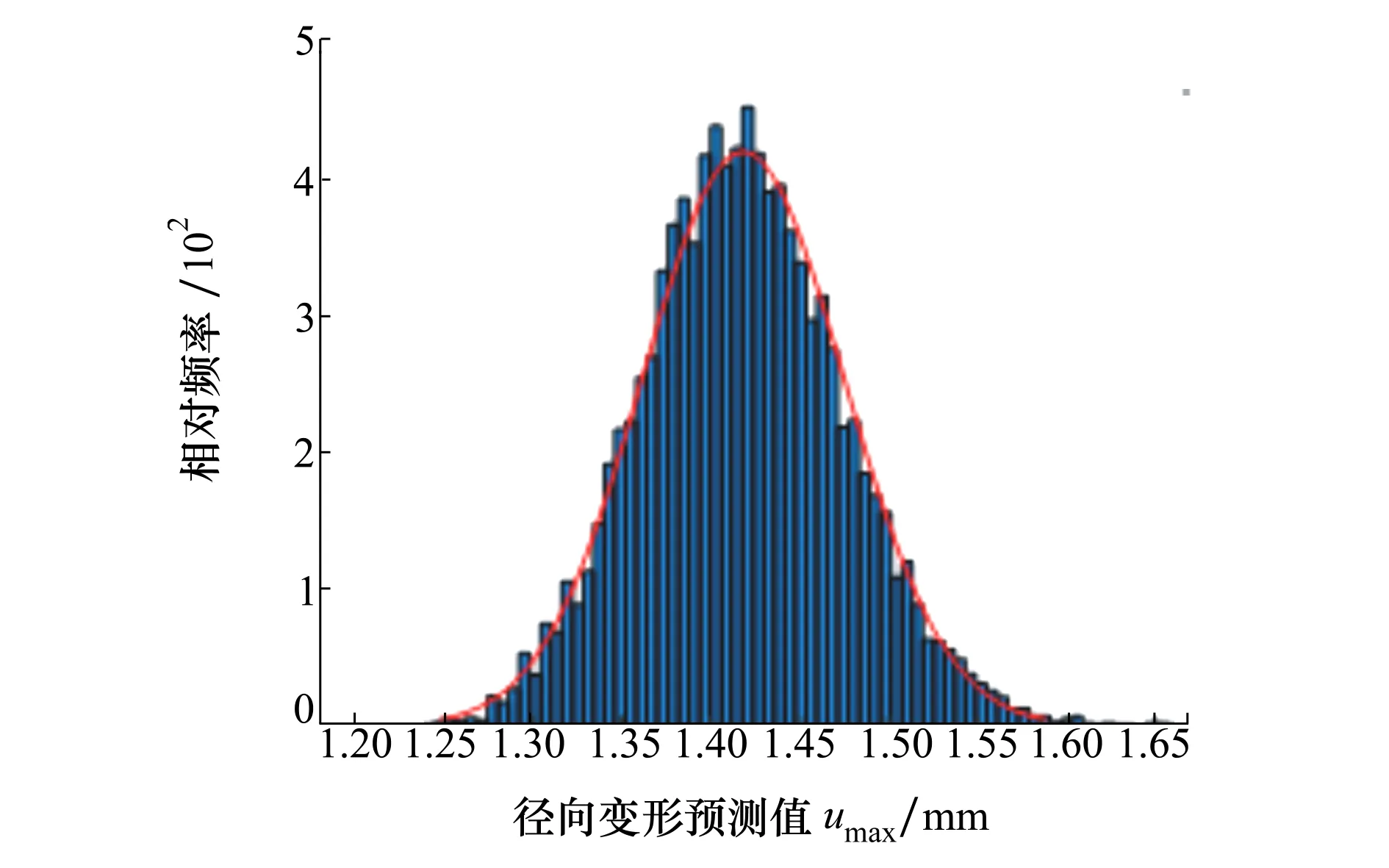
圖8 低壓壓氣機葉盤徑向變形分布直方圖

3 粒子群極值Kriging模型驗證

3.1 建模特性

為了說明PSOEKM在建模特性方面的優勢,基于測試樣本,通過均方根誤差ERMS和平均相對誤差Ear對其建模精度進行研究,其計算原理見(16)式。在PSOEKM建模特性過程中,通過極值響應面法(extremum response surface method,ERSM)和極值Kriging模型(extremum Kriging model,EKM)進行對比分析。需要說明的是:所有的計算在相同的計算環境下執行;ERSM和EKM模型均是采用相同的訓練樣本構建;在建模精度分析過程中,以低壓壓氣機葉盤徑向變形動態確定性分析結果作為參考;在建模效率方面,則是以ERSM建模時間作為參考。建模精度與效率分析結果如表2所示。

(16)

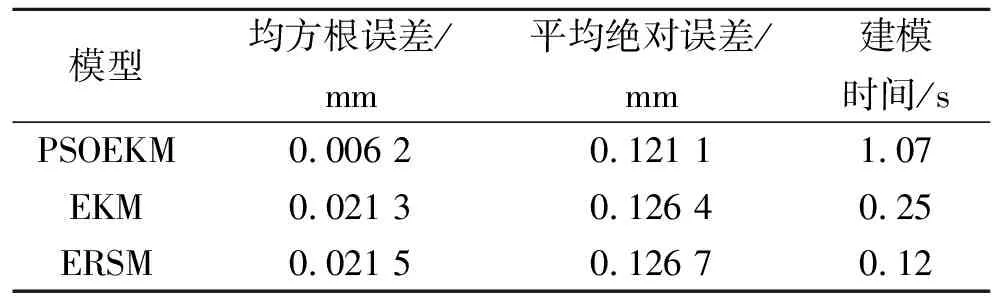
表2 建模精度與效率分析結果

由表2可以看出,PSOEKM的建模時間相對于EKM和ERSM略有增長,其原因是PSO在模型超參數尋優過程中存在多次迭代計算,但是其建模效率是可接受的。在建模精度方面,相較于EKM和ERSM,所提出的PSOEKM具有一定的優勢,PSOEKM的均方根誤差和平均絕對誤差小于ERSM和EKM的均方根誤差和平均絕對誤差,并且PSOEKM的建模精度相對于ERSM和EKM分別提高了4.62%和4.38%。因此,在建模效率可接受范圍內,PSOEKM在建模精度方面具有明顯的優勢。

3.2 仿真性能

PSOEKM方法的仿真性能主要從仿真效率和分析精度兩方面進行研究,結合多種方法對比分析的手段加以說明,其中所用的方法有直接模擬法、ERSM和EKM。基于表1中輸入變量數值隨機的分布特征,分別將4種方法用于執行不同頻次(102,103和104)的MC抽樣,實現低壓壓氣機葉盤徑向變形時變可靠性分析。其中,由于計算限制沒有執行104次直接模擬。此外,在仿真性能分析過程中,以直接模擬的分析結果作為參考。基于ERSM、EKM和PSOEKM的仿真性能分析結果如表3～5所示。

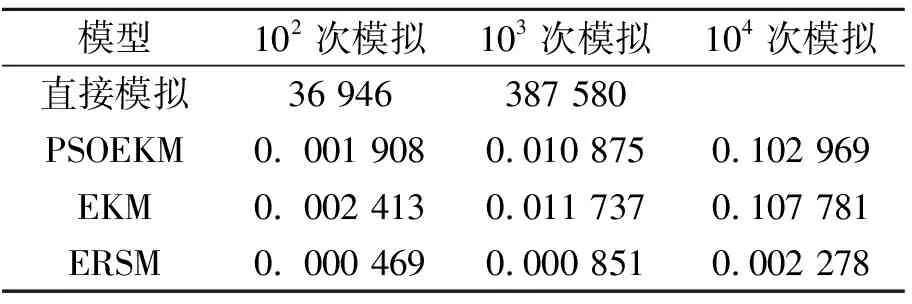
表3 仿真效率分析結果 s

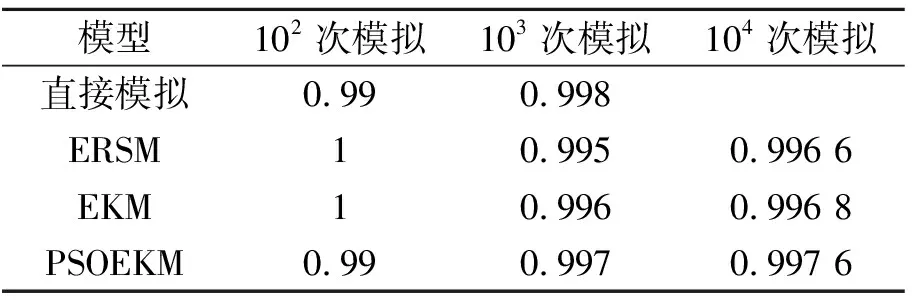
表4 仿真可靠性分析結果

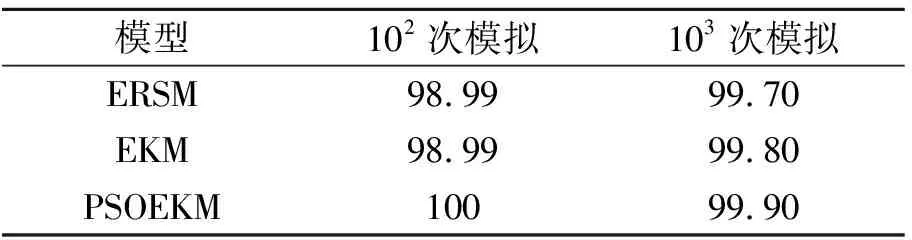
表5 仿真精度分析結果 %

由表3可知,代理模型(包括PSOEKM、EKM和ERSM)的仿真時間遠遠小于直接模擬的仿真時間,由表4～5可以看出,在不同的仿真模擬次數下,PSOEKM的仿真結果優于ERSM和EKM的仿真結果,并且其分析結果與直接模擬的結果最為接近;相較于ERSM和EKM,PSOEKM的仿真精度分別提升了0.61%和0.11%。因此,PSOEKM在仿真特性方面具有一定的優勢。

4 結 論

基于Kriging模型,結合PSO與極值思想,提出了PSOEKM方法,在考慮流體載荷和結構載荷交互作用的情況下,本文實現航空發動機低壓壓氣機葉盤徑向變形時變可靠性分析,并通過方法對比驗證了所提出方法的有效性和可行性。本文主要結論如下:

1) 考慮多種時變載荷的影響,開展了低壓壓氣機葉盤徑向變形動態確定性分析,獲取輸出響應隨時間變化規律,并確定了輸出響應極值與研究時刻點;

2) 基于PSOEKM實現了低壓壓氣機葉盤徑向變形建模,通過大量仿真模擬,當徑向變形許用值為1.594×10-3m時,其可靠概率為99.76%;

3) PSOEKM在建模精度方面具有一定的優勢,其精度相對于ERSM和EKM分別提高了4.62%和4.38%;

4) 在不同模擬次數下,在仿真效率滿足工程需求的前提下,PSOEKM仿真精度均優于ERSM和EKM。