基于和聲差分進化混合算法的橫向磁場電機優化設計
袁小慶, 周彤, 姬俊杰, 劉宇軒, 杜曉東
(西北工業大學 機電學院, 陜西 西安 710072)
橫向磁場電機(transverse flux motor,TFM)最早是由德國的Weh教授和他的合作者提出[1],TFM運動方向與磁場方向不在同一個平面內,實現了結構上的電磁解耦[2],進一步提高了最大轉矩密度。國內外的學者關于TFM提出了很多新型拓撲結構[3-6],但對于TFM具體參數的優化研究較少,大多憑借經驗公式和有限元分析對其進行優化設計, 難以得到全局最優解。也有部分學者將智能優化算法[7]應用到TFM優化設計中,如中國科學院大學邱書桓等利用遺傳算法對一款圓筒形錯相式TFM進行優化[8],增大了齒磁密,減少了漏磁。蘭州理工大學包廣清等利用改進的粒子群算法對一款TFM進行優化[9],提高了工作效率,縮減了制造成本。
本文將和聲搜索(harmony search,HS)算法[10]與差分進化(differential evolution,DE)算法[11]相結合,并引入精英保留策略[12],得到一種改進的和聲差分進化混合(improved harmony search and differential evolution,IHSDE) 算法。基于該算法,以最大轉矩密度和生產成本為優化目標對一種新型盤式雙向交鏈橫向磁通永磁電機[13](disk-type bipolar crosslinking transverse flux permanent-magnet motor,DBC-TFPM)進行優化設計,通過Matlab仿真得到了優化變量的全局最優解,驗證了算法的有效性。
1 IHSDE算法原理
IHSDE算法同時具有HS算法與DE算法的優點,以HS算法為主體,在新和聲的生成方式上加入了DE算法的思想,在更新和聲記憶庫時引入精英保留策略有效改善了算法的性能。
1.1 初始記憶庫
在進行優化前,采用HS算法生產初始記憶庫的方式來隨機化初始記憶庫HM={x1,x2,…,xN},通過如下方式生成
xi,j=lj+r·(uj-lj),j=1,2,…,d,i=1,2,…,N
(1)
式中:xi,j為第i個和聲的第j維分量;uj和lj為xi,j取值的上下界;N為和聲的總數;d為和聲的維度;r為0~1之間的隨機數。
1.2 生成新和聲
標準HS算法主要通過記憶選擇、局部調諧和隨機生成3種方式來尋找合適的新解,在這個過程中融合DE算法,即基于2個個體的差分項產生新個體,可以減少隨機生成的新個體數量,從而提高運算的收斂速度,該步驟為
(2)
式中:xnew,j為新的和聲分量;ra為1~N的隨機數;r′為0~1的隨機數;HMCR為記憶選擇概率;r2,r3∈{1,2,3,…,N}為互不相等的整數且都不等于i;F為DE算法的比例因子,取值是0~1之間的數;cr為個體中變量交叉概率。
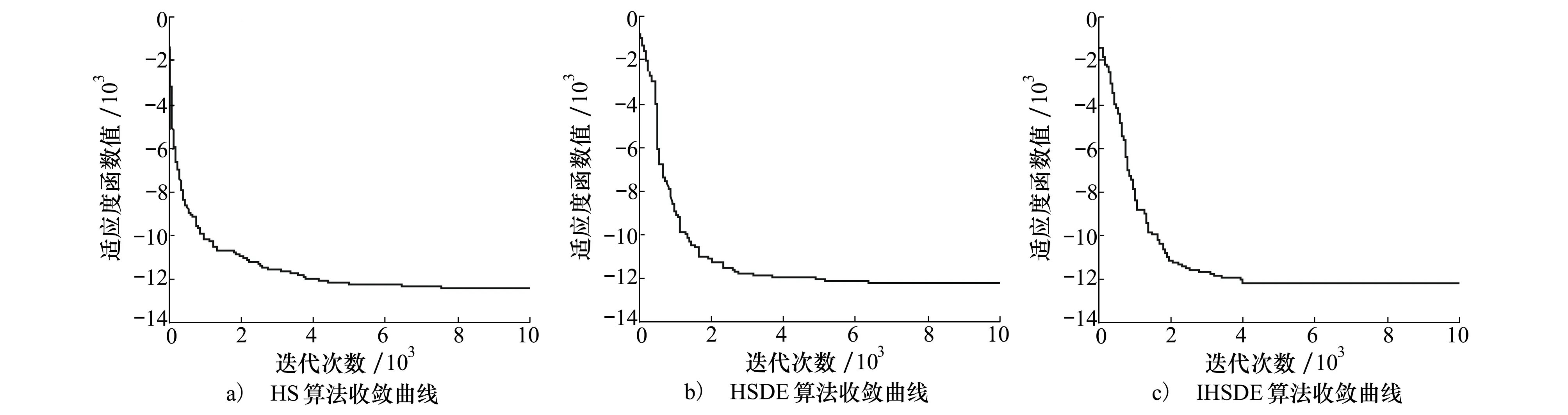
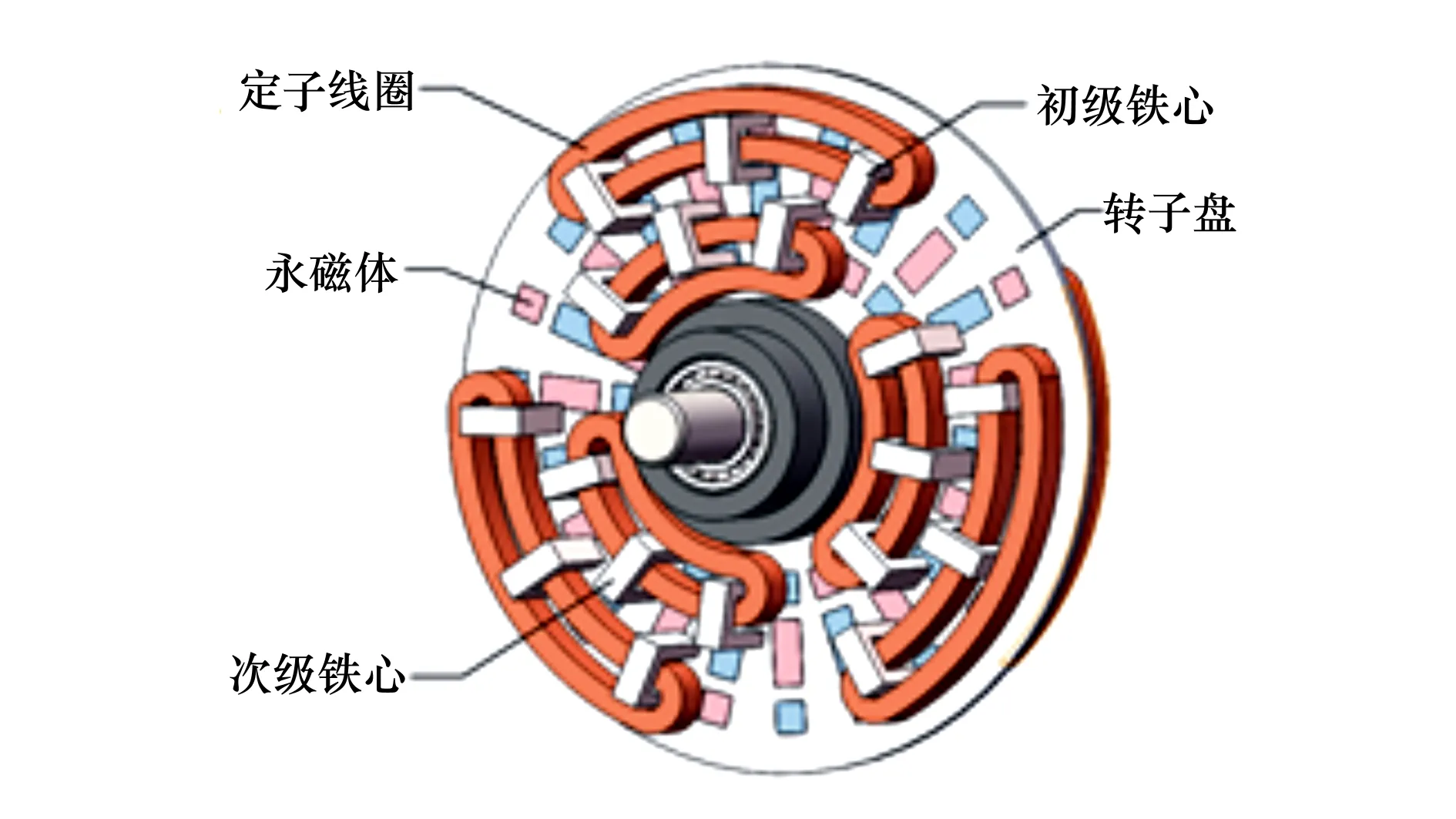
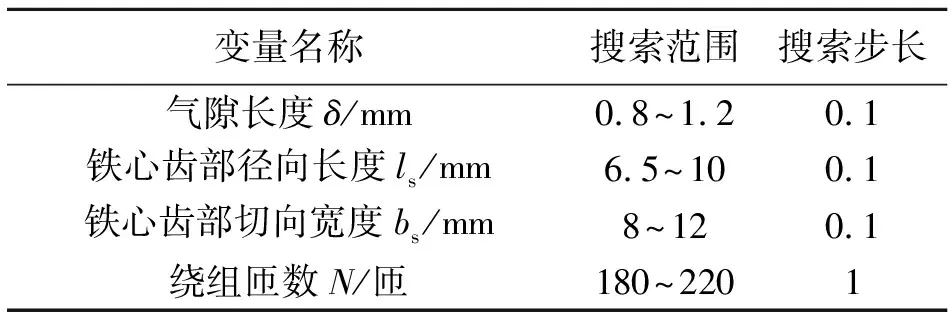
對于r′ (3) 式中:r″和r?分別為0~1的隨機數;bw為音調微調帶寬。 圖1為IHSDE算法流程圖。對每一代和聲依據其適應度值進行升序排列,選擇第一組和聲與上一代的第一組和聲進行比較,若該和聲適應度更好,則將其加入精英和聲數據庫,其余和聲依據算法規則進行調整,之后將該精英和聲加入調整后的記憶庫并重新進行升序排列。精英保留策略保證了在迭代過程中產生的最優和聲不會被破壞,提高了IHSDE算法在搜索過程中的收斂性。 為了驗證該混合算法有效性,基于Matlab編寫HS算法、HSDE算法以及IHSDE算法,利用含有30個變量的標準測試函數Schwefel 2.26[14]進行測試,3種優化算法的函數測試情況如圖2所示。 圖2 3種優化算法的函數測試情況 Schwefel 2.26函數表達式 |xi|≤500 (4) 其最優狀態和最優值為 min(f(x*))=f(420.968 7,…,420.968 7)= -12 569 (5) 當計算出的最優解大于-12 000時,認為本次求解屬于早熟。每種算法均重復計算該函數50次,其搜索能力如表1所示。從表1中可知,HSDE算法的收斂速度雖然比HS算法有了很大提高,但也造成了早熟概率的提高。在加入精英保留策略后,IHSDE算法收斂速度有所提升,同時早熟概率大大降低,接近0,結果更為可靠。測試結果說明了IHSDE算法可有效求解并優化多維復雜函數的極值問題,也可以用于電機優化設計中多維函數求解問題。 表1 3種優化算法搜索能力比較 本文在如圖3所示的DBC-TFPM的基礎上進行優化設計。計算最大轉矩密度之前,給出了鐵心和永磁體的主要尺寸的幾何定義,如圖4所示。 圖3 DBC-TFPM結構圖 圖4 鐵心和永磁體尺寸平面圖 (6)式給出了最大轉矩密度公式,具體推導過程可參考文獻[13]。 (6) 式中:m為電機的相數;Ia為單相繞組電流有效值;φδ為每極氣隙磁通量;n為單相繞組內的鐵心數;N為單相繞組的有效匝數;V為電機體積,D為電機直徑;L為電機軸向長度。 每極氣隙磁通量φδ估算為 φδ=BδAs=Bδlsbs (7) 式中:As是定子鐵心齒部面積,As=lsbs;Bδ為氣隙剩磁密度。 氣隙剩磁密度Bδ可表示為 (8) 電機單相繞組電流I和匝數N與電流密度J關系可以表示為 NI=Jsd=Jlchcsf (9) 式中:sf為槽滿率,其值與繞線的工藝和所選線徑及材質相關;sd為導線橫截面積。 為方便計算,令 (10) 由圖4可知 (11) 式中:ε為線圈與定子鐵心內圈的間隙,ε=1 mm;z為定子鐵心壓線盤到定子鐵心齒部的距離。考慮到螺釘的安裝和磁導的大小,取z=5 mm。 電機軸向長度D和定子盤直徑L滿足 (12) 式中,pz為電機轉子極對數。 將(7)~ (12)式帶入(6)式中,得 (13) 電機的優化設計本質上是多目標優化問題,此類問題一般可以描述為 (14) 式中:X=[x1,x2,…,xn]為電機的優化變量,如結構參數等;f(X)為優化的目標函數;gi(X)為優化約束條件。 DBC-TFPM應用于新能源汽車時,作為動力核心部件需要提供足夠的輸出轉矩,由于車內空間緊湊,還需盡可能減小電機體積。此外,橫向磁場電機特殊的結構設計導致其生產成本較高,在保證性能的前提下,應盡可能地降低成本。因此,本文選擇最大轉矩密度和生產成本為優化子目標。為了消除數量級不同帶來的優化誤差,設計優化目標函數為 (15) 式中:STm和STm0分別為優化后電機和原型機的最大轉矩密度;C和C0分別為優化后電機和原型機的有效物料成本;q1和q2為子目標函數的權重系數; 10是為了使函數計算結果為正而引入的常數。 電機的有效物料成本C為 C=CCu·GCu+CFe·GFe+CPM·GPM+CAl·GAl (16) 式中:CCu,CFe,CPM,CAl分別為銅、硅鋼片、釹鐵硼永磁體、鋁的價格;GCu,GFe,GPM,GAl分別為銅、硅鋼片、釹鐵硼永磁體、鋁的質量。 本文中,假設銅的價格為60元/kg,硅鋼片的價格為10元/kg,釹鐵硼永磁體的價格為120元/kg,鋁的價格為30元/kg。 結合公式(13),選取對DBC-TFPM性能影響較大的氣隙長度δ、繞組匝數N、鐵心齒部徑向寬度ls和鐵心齒部切向寬度bs為優化設計變量X,如下所示 (17) 電機的約束條件是為了讓電機優化后滿足一些實際生產中的工藝要求、客戶需求和技術規范等。約束條件均為不等式約束,按照約束的性質,可以分為性能約束和幾何約束。選擇約束條件時需要考慮以下幾個方面:①符合電機生產制造的工藝標準,比如繞組的槽滿率應當符合嵌線工藝的要求;②電機的性能指標符合產品的技術規范及客戶的需求;③電機的各零部件幾何尺寸符合電機的設計規范。 綜上,約束條件表達式為 (18) 式中:T0為原型機的輸出轉矩;V0為原型機體積;sf0為原型機繞組線圈槽滿率;C0為原型機成本。 由于各約束條件數量級相差巨大,不能直接用于電機的優化設計,對其進行規范化處理,表示為如下的相對值形式 (19) 由于IHSDE算法是一種無約束優化算法,只能用來計算無約束問題,需要把目標函數轉化為無約束極值問題,為此引入罰函數構造增廣目標函數。本文選用的罰函數[14]為 (20) 式中:U為一個常數,表示當函數違反約束時施加的最小約束值;ωi為懲罰系數,對于不同的約束,根據其影響大小使用不同的懲罰系數。 最終構造出來的增廣目標函數F(X)為 (21) 電機散熱要求較高,選擇水冷散熱,電流密度選擇10 A/mm2。槽滿率大小的選擇與繞線的工藝和所選線徑及材質相關,本文初選0.65。DBC-TFPM單相定子鐵心數n為6,轉子極對數pz為11。 在編寫優化程序時,選定各優化變量的變化范圍以及搜索步長如表2所示。 表2 變量取值范圍及搜索步長 為體現不同權重系數對優化效果的影響,選取2組權重系數做對比:①q1=0.4,q2=0.6,側重于減小生產成本;②q1=0.6,q2=0.4,側重于增大最大轉矩密度。用Matlab編寫優化程序,仿真計算得到優化目標函數相關變化曲線如圖5所示,優化設計變量相關變化曲線如圖6所示。由圖5可知,在迭代運算過程中,雖然子目標函數中的成本、轉矩和最大轉矩密度曲線有所波折,但總體目標的適應度函數值一直在穩步增長,說明整個記憶庫中的和聲群體趨向于最優化。在算法計算后期,總適應度函數值基本保持不變,此時已經滿足收斂條件。由圖6可知在迭代過程中不斷有新的隨機變量生成,在達到一定迭代次數后整體慢慢收斂。 圖5 優化目標函數相關變化曲線 圖6 優化設計變量變化曲線 經過優化算法程序計算,得到優化后的相關電機參數,將其與原型機的參數進行對比,如表3所示。 表3 電機優化前后參數對比 分析上表數據可知,第一組權重系數下電機的最大轉矩提高26.3%,最大轉矩密度提高24.1%,生產成本降低了3.3%;第二組權重系數下電機的最大轉矩提高34.6%,最大轉矩密度提高32.5%,生產成本降低了1.8%,均取得了預期的優化效果。 本文提出了IHSDE算法,利用標準測試函數Schwefel 2.26對HS算法、HSDE算法和IHSDE算法進行性能測試,得出IHSDE算法收斂速度更快、早熟概率更低并且全局搜索能力更好,滿足電機優化設計的要求。在Matlab平臺編寫IHSDE算法程序對DBC-TFPM進行參數優化,仿真結果驗證了該算法的正確性。該算法不僅適用于橫向磁場電機的優化設計,也為解決其他多目標優化問題提供了參考,具有廣闊的應用前景。1.3 精英保留策略
2 算法性能測試

3 DBC-TFPM尺寸和性能分析





4 DBC-TFPM參數優化
4.1 選擇優化目標函數
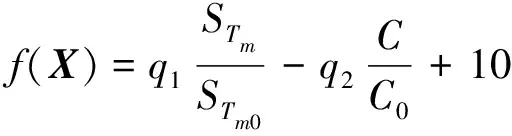
4.2 選擇優化設計變量
4.3 設定約束條件
4.4 構造增廣目標函數

4.5 主要參數和變量搜索范圍確定
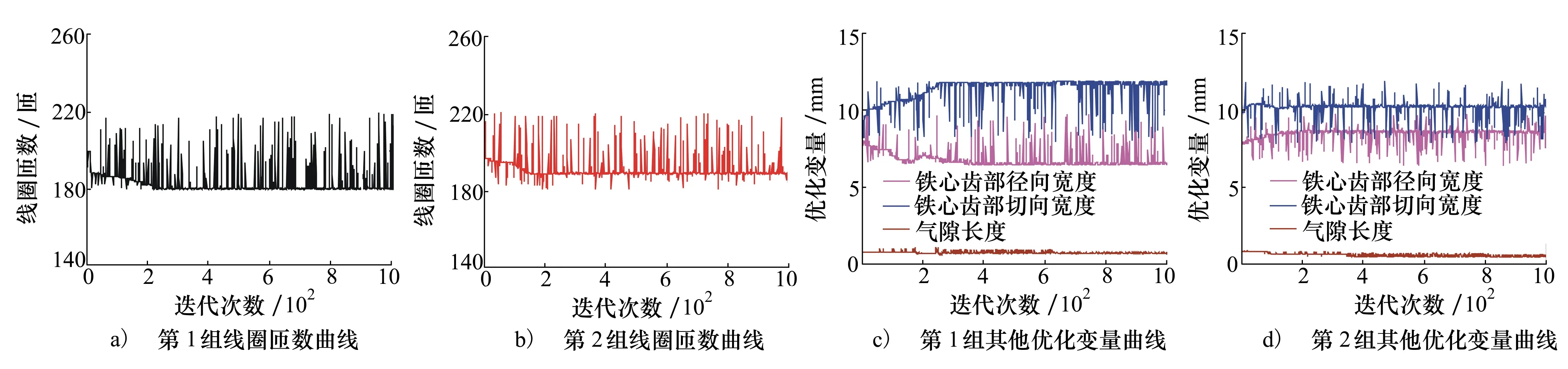
4.6 優化分析


5 結 論

