融合動態收斂因子與黃金正弦的花朵授粉算法
高翻翻,丁正生
(西安科技大學 理學院,陜西 西安 710600)
0 引言
花朵授粉算法(flower pollination algorithm, FPA)[1]是一種模擬花朵授粉過程的優化算法,該算法具有參數少、魯棒性好、易調節和易實現的優點。
國內外對FPA的研究主要分為算法的優化[2-4]和應用[5-7]兩大類。文獻[8]提出了融合正弦余弦算法和精英算子的花朵授粉算法,與FPA相比尋優精度得到了改善,但缺乏應用,該算法的可行性有待商榷。文獻[9]提出了一種求解置換流水車間調度問題的新型花朵授粉算法,但對測試函數的結果并未達到理論最優值,還需改進。文獻[10]提出了一種求解旅行商問題的離散花朵授粉算法,雖得到了較好的尋優效果,但其所花費的時間過長。
上述改進策略雖對FPA的性能有所提升,但仍存在收斂精度和跳出局部最優能力偏低等不足,故許多學者通過各種改進方法來幫助FPA算法跳出局部最優,如文獻[11]用霍爾頓(Halton)序列來初始種群質量,文獻[12-13]增加了高斯(Gauss)變異算子,文獻[14-15]分別引入了定向變異策略和量子搜索機制,文獻[16-17]加入了柯西(Cauchy)變異等。雖然以上改進均提高了算法跳出局部最優的能力,卻導致優化效果不明顯、無法收斂到0等問題,基于此,本文提出了一種融合動態收斂因子與黃金正弦的花朵授粉算法(flower pollination algorithm combining dynamic convergence factor and golden sine, DGSFPA)。借助仿真實驗和案例分析,驗證了DGSFPA能夠更有效地跳出局部最優,同時提高了FPA的尋優精度和收斂速度。
1 花朵授粉算法
花朵授粉算法是模擬顯花植物花朵傳粉的過程,要實現該算法需滿足以下幾個準則:
(Ⅰ)攜帶花粉的傳粉者(蜜蜂,鳥)利用Lévy飛行進行傳粉,這種生物異花授粉被認為是全局授粉。
(Ⅱ)通過風和水等自然因素進行傳粉的非生物自花授粉被認為是局部授粉。
(Ⅲ)花的恒定等于繁衍概率,其值與所涉及的兩種花的相似性成正比。
(Ⅳ)轉換概率p∈[0,1]調節全局授粉和局部授粉,由于自然因素的影響,使局部授粉具有更顯著的p值,在整個傳粉過程中占主導作用。
花朵授粉算法主要有兩個階段:
階段一:若轉換概率p>rand,rand是[0,1]的隨機數,則昆蟲通過攜帶花粉配子進行異花授粉(全局授粉),此時花粉的位置更新方法為:
(1)
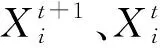
(2)
其中:縮放因子λ=1.5;Γ(λ)表示標準伽馬函數。
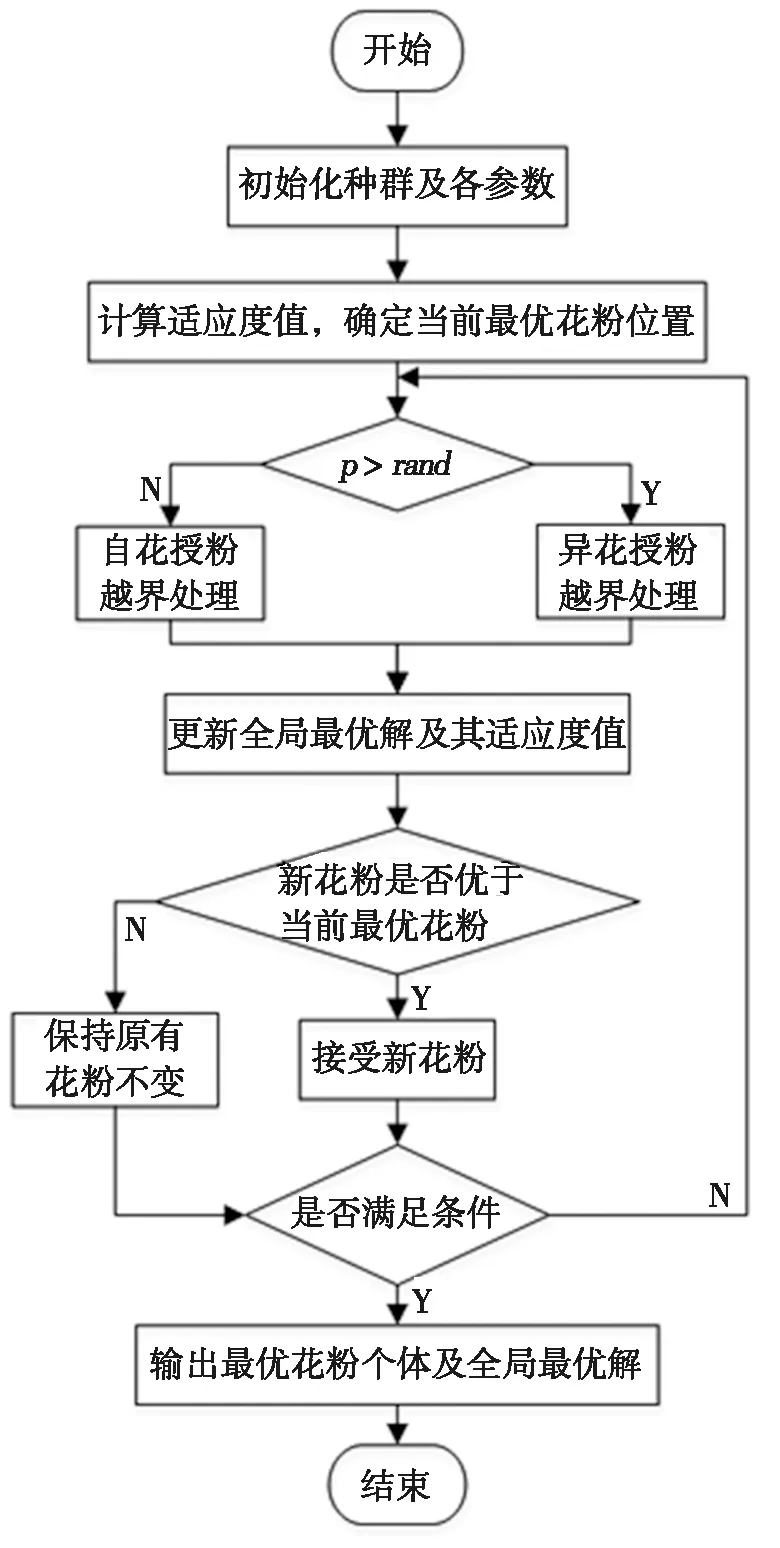
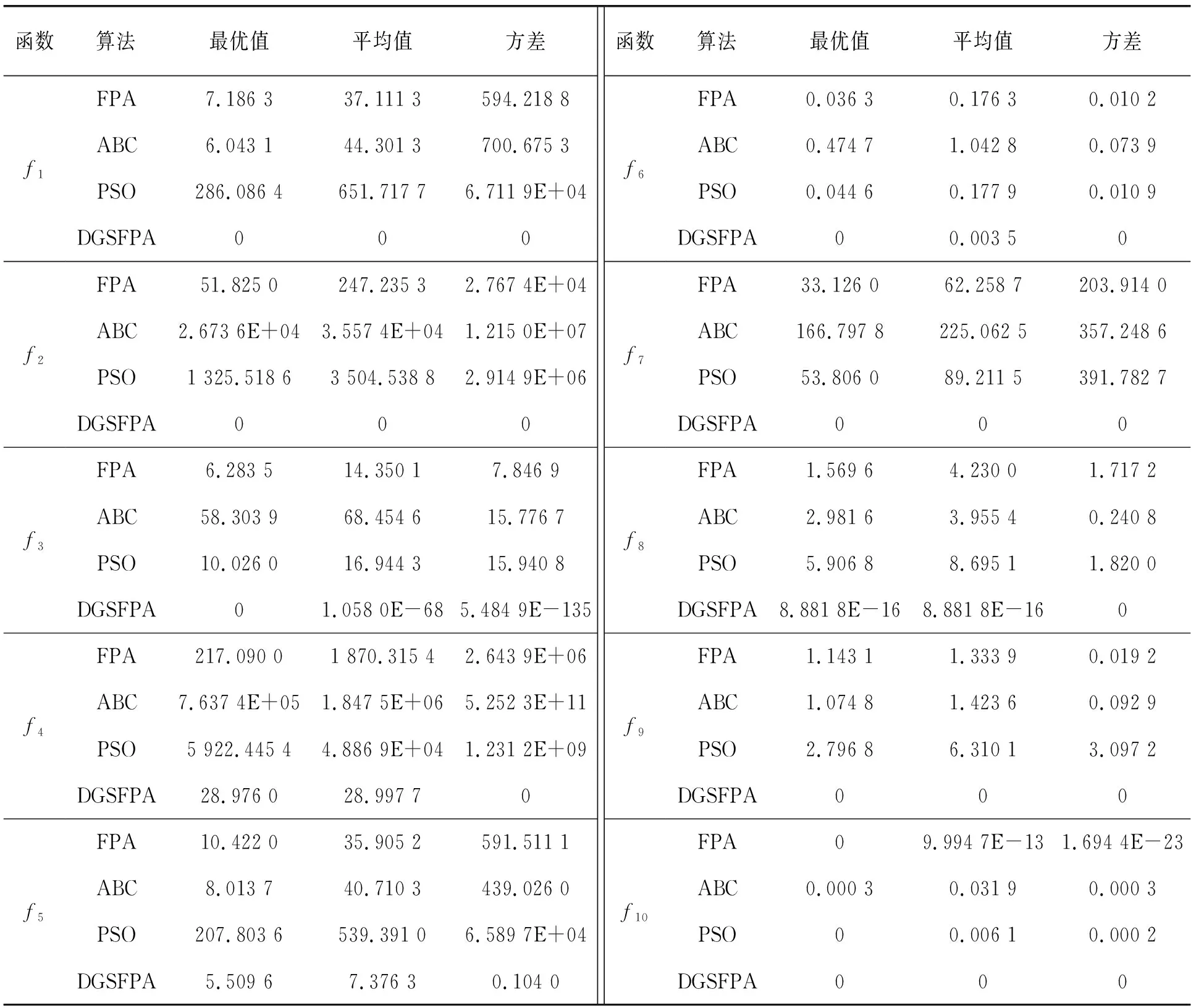
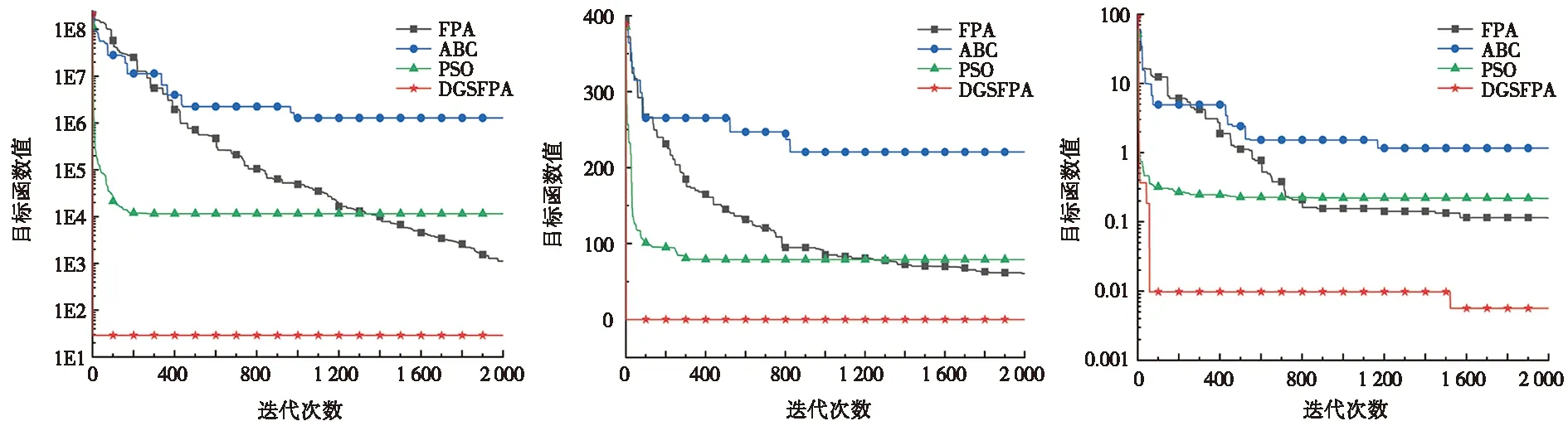
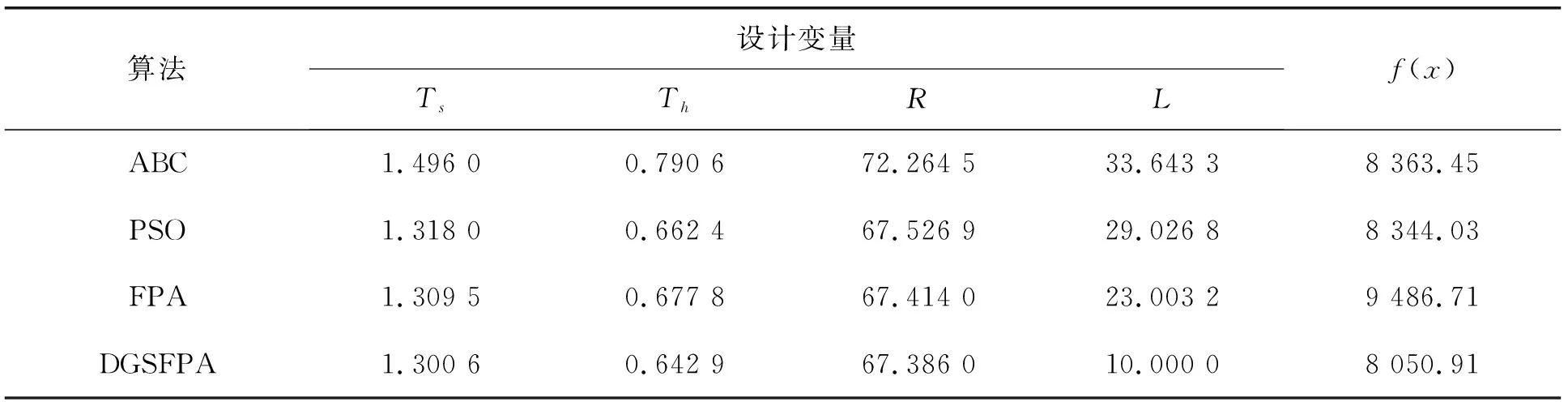
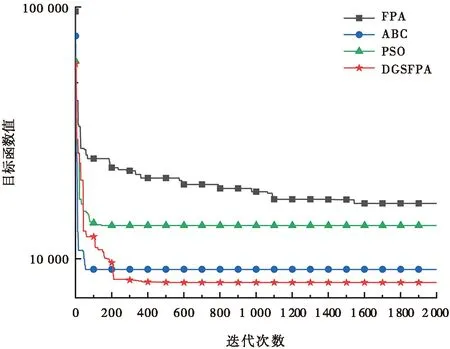
階段二:若轉換概率p (3) 鯨魚優化算法[18]在全局搜索中加入動態收斂因子,可以改善算法的收斂精度,受此啟發,本文在異花授粉的位置更新處引入動態收斂因子,該因子通過結合傳粉者的Lévy飛行軌跡,不僅能提高算法的收斂精度,而且可以增強全局勘探的能力。 改進后的異花授粉位置更新方法為: (4) 其中:a為動態收斂因子,其計算方式為: (5) 其中:t為當前迭代次數;N_iter為最大迭代次數;由于迭代次數的增加,a值逐漸減小到0。 傳統FPA在自花授粉過程中采用的位置更新方法,其搜索空間較廣泛,尋優效果不佳,而文獻[19-20]提出了黃金正弦算法(golden sine algorithm,Golden-SA),該算法中的參數R1和R2分別控制位置更新的距離和方向,有效指引花粉個體向最優個體靠近,并增加了種群之間的信息交流。因此,在自花授粉中嵌入黃金正弦算法,即在位置更新階段引入黃金比例系數,極大程度縮減了搜索空間,有利于跳出局部最優,達到提升尋優能力的目的。 改進后的自花授粉位置更新方法為: (6) 其中:r1,r2是隨機數,且r1∈[0,2π],r2∈[0,π],它們所代表的含義同R1和R2一致;x1=-π+(1-τ)2π和x2=-π+2πτ是通過黃金分割法得到的系數,τ為黃金分割數。 本文提出的DGSFPA的操作流程如圖1所示,具體的計算步驟如下: 圖1 DGSFPA流程圖 步驟1:初始化。n為種群規模,d為搜索空間的維數,p為轉換概率,t為迭代次數,N_iter為最大迭代次數。 步驟2:適應度值的評價。計算n個種群的適應度值,通過比較,將最優適應度值對應的花朵確定為當前最優花粉個體(當前最優解)。 步驟3:授粉形式的轉換。 (Ⅰ)若轉換概率p>rand成立,執行異花授粉階段,該階段采用改進后的異花授粉來進行花粉位置的更新,如式(4)所示,隨后進行越界處理。 (Ⅱ)若p 步驟4:判斷是否更新當前最優花粉個體。若步驟3得到的新解比當前最優解還好,則將此新解設為當前最優解,更新花粉個體,否則,將不發生任何改變。 步驟5:判斷循環是否結束。若已達到最大迭代次數N_iter,則循環結束,否則返回步驟3繼續進行循環,直到滿足條件為止。 步驟6:輸出最優花粉個體g*及全局最優解。 采用10個測試函數對DGSFPA進行仿真實驗,將DGSFPA與FPA、粒子群算法(particle swarm optimization,PSO)[21-22]及人工蜂群算法(artificial bee colony,ABC)[23]作對比,用來驗證DGSFPA的尋優能力。 為了實驗的公平性,本文將4種算法的共有參數設定一致,即種群容量20,最大迭代次數2 000,FPA、DGSFPA涉及的轉換概率p=0.8,PSO中c1=c2=1.5。 本文選取10個標準測試函數,即Sphere(f1)、Schwefel1.2(f2)、Schwefel2.21(f3)、Rosenbrock(f4)、Step(f5)、Quartic(f6)、Rastrigin(f7)、Ackley(f8)、Griewank(f9)和Schaffer(f10),其中函數f1~f9的維數是30,f10的維數是2。 用4種算法分別對每個測試函數獨立運行50次,并記錄它們的最優值、平均值和方差,其尋優結果如表1所示。 由表1可知:對于函數f1,f2,f7,f9,f10,DGSFPA的3個評價指標均達到了理論最優值0,說明DGSFPA的尋優能力在這5個函數上是最好的。對于函數f3,f4,f5,f6,f8,DGSFPA雖未達到理論最優值0,但其尋優結果與理論最優值非常接近,如函數f3,相比于FPA、ABC、PSO,DGSFPA,在平均值指標上均提高了69個數量級。DGSFPA在函數f1,f2,f4,f6,f7,f8,f9,f10上的方差均達到了0,其他3種算法在所有函數上的方差均未達到0,說明DGSFPA的穩定性更強。綜上所述,相比于其他3種算法,DGSFPA無論在低維還是高維函數中,尋優能力都更強。 表1 4種算法的尋優結果 為更直觀地表明改進算法的尋優能力,給出4種算法在函數f4,f6,f7上的收斂曲線圖,如圖2所示。 (a) 函數f4收斂曲線圖 (b) 函數f6收斂曲線圖(c) 函數f7收斂曲線圖 從圖2可以看出:4種算法中,DGSFPA的收斂曲線下降速度最快,PSO次之。圖2a和圖2b中FPA的曲線在規定迭代次數內還未找到全局最優,而DGSFPA的曲線未到100次迭代就已經取得了全局最優解,這表明改進算法的尋優效果更強。圖2c中FPA和ABC的曲線在后期迭代中跳出了局部最優,但又陷入另一個局部最優中,而DGSFPA的曲線下降速度最快,且在1 500次迭代左右跳出了局部最優,找到了全局最優解,這說明FPA在自花授粉階段中引入黃金正弦算子后,能夠提高算法跳出局部最優的能力。 壓力容器設計優化問題[24]是經典的工程設計優化問題,由容器厚度Ts、封頭厚度Th、內半徑R和圓柱形長度L共4個設計變量構成,其目標是在滿足一定的約束條件下優化這4個設計變量來最小化總成本(材料、成型和焊接的成本),相當于求有約束條件的目標函數最小值問題。 壓力容器設計問題的目標函數為: x=[x1,x2,x3,x4]=[Ts,Th,R,L]; s.t.g1(x)=-x1+0.019 3x3≤0; g2(x)=-x2+0.009 54x3≤0; g4(x)=x4-240≤0; 1×0.062 5≤x1,x2≤99×0.062 5,10≤x3,x4≤200。 (7) 為了驗證本文算法在壓力容器設計優化問題中的有效性,采用FPA、ABC、PSO及DGSFPA 這4種算法分別對該問題進行求解,并將所得實驗結果進行對比分析。算法參數設置與第3節仿真實驗中相似,種群容量為20,最大迭代次數為1 000,4種算法分別獨立運行50次,并分別記錄其最優值、平均值和方差,具體實驗結果如表2所示。 表2 4種算法解決壓力容器設計問題總成本的實驗結果 元 由表2可知:在壓力容器設計優化問題中,DGSFPA得到的總成本是最小的,ABC次之。DGSFPA平均值比FPA減少5 270.82元,與ABC相比減少876.72元,再次說明改進算法的尋優能力最好。DGSFPA的方差為0,其他算法的方差均不是0,這表明DGSFPA在尋找全局最優解時穩定性最好。 表3是4種算法在分別解決壓力容器設計問題時,所得最優結果對應的各個變量值。由表3可知:DGSFPA所得壓力容器中4個設計變量值是最小的,因而其總成本也最小。 表3 4種算法解決壓力容器設計問題的各個變量結果對比 圖3是4種算法求壓力容器總成本的收斂曲線圖。從圖4中可知:4種算法中,DGSFPA所得到的目標函數值是最小的,ABC次之。DGSFPA的曲線下降速度較快,更早地跳出局部最優到達最優解附近,降低適應度值直到穩定;而FPA的曲線在前期迭代時易陷入局部最優,且收斂緩慢,表明DGSFPA的尋優能力更強。綜上所述,從實際應用的實驗結果可以證明,本文提出的DGSFPA在解決工程設計優化問題時,求最優解的效果更好。 圖3 4種算法求總成本的收斂曲線圖 本文在傳統FPA的異花授粉和自花授粉兩階段中分別引入了動態收斂因子和黃金正弦算法,來提高算法的收斂精度和跳出局部最優的能力,并將4種算法在10個測試函數上進行比較分析,結果表明改進算法具有良好的尋優能力。將DGSFPA應用到壓力容器設計優化問題中,與FPA、PSO、ABC 3種優化算法相比,改進算法在求最優解質量方面得到了更好的效果。今后研究重點是如何將DGSFPA應用到其他領域。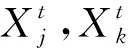
2 改進的花朵授粉算法
2.1 改進的異花授粉位置更新方法
2.2 改進的自花授粉位置更新方法
2.3 DGSFPA步驟
3 仿真實驗
3.1 實驗參數設定
3.2 測試函數
3.3 實驗結果分析
4 案例分析

5 結束語

