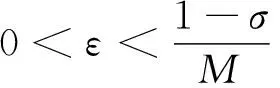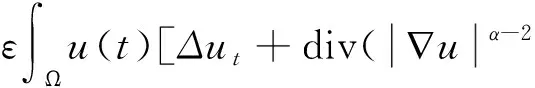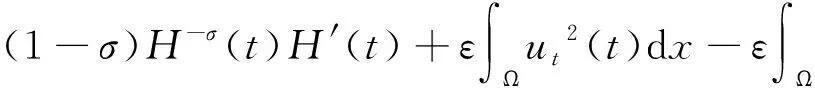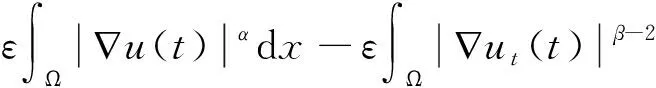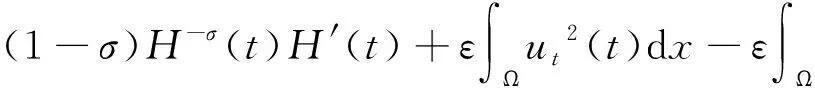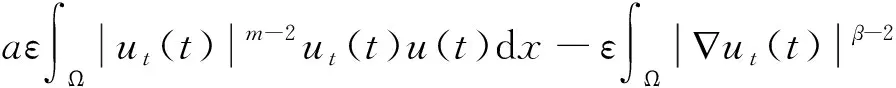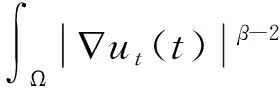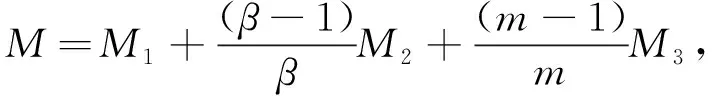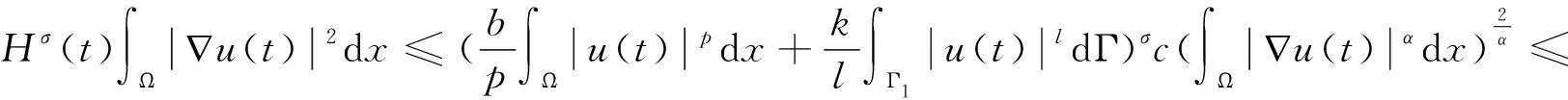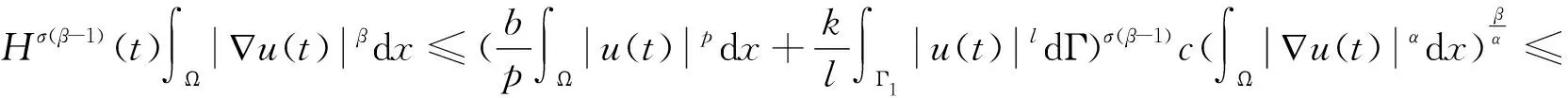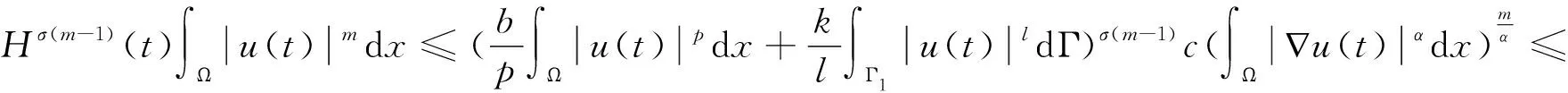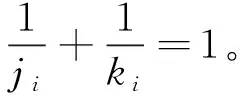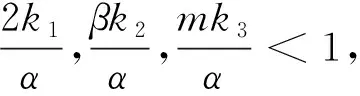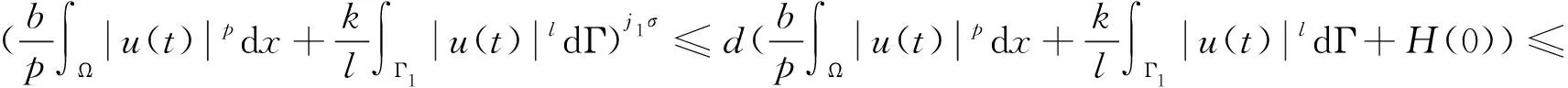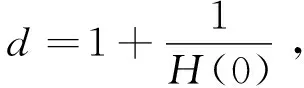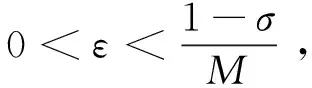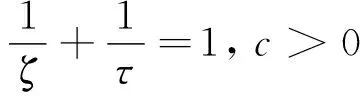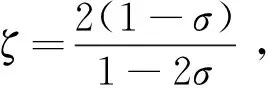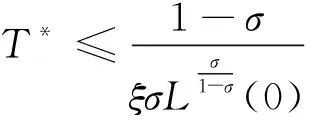具有內部及邊界源項的擬線性波方程解的整體不存在性
任佳敏
(山西大學 數學科學學院,山西 太原 030006)
0 引言
本文研究以下具有聲學邊界條件,非線性內部及邊界源項的擬線性波方程解的整體不存在性,
其中:a,b,k>0,α,β,m,p,l>2,Ω是Rn(n≥1)的一個有界正則區域且?Ω=Γ0∪Γ1。這里Γ0,Γ1均為閉的且互不相交,函數h(x),f(x),q(x):Γ1→R+是本性有界的且在Γ1上有:0 聲學邊界條件由Morse和Ingard在文獻[1]中首次提出,并在文獻[2]中得到了完善和發展。文獻[3]研究了具有非線性阻尼項和源項的擬線性雙曲型方程解的能量衰減和爆破。文獻[4]研究了具有內部源項j1(u)和邊界源項j2(u)的波方程局部解的存在唯一性、解的全局存在性及j1(u)=0時解的某一指定范數增長率。 文獻[5]研究了以下具有多孔聲學邊界條件的非線性波動方程解的整體不存在性,文中用到了經典的勢阱方法和凹性方法, 文獻[6-8]證明了一類具有非線性阻尼項和源項的波方程解的整體不存在性。文獻[9-10]研究了具有聲學邊界條件的黏彈性波方程解的存在性、爆破和衰減。文獻[11-12]證明了非線性發展方程整體解的不存在性。文獻[13]研究了具有時滯和聲學邊界條件的擬線性波方程解的整體不存在性。文獻[14-18]均利用伽遼金逼近法得出方程弱解的存在性。文獻[19]利用能量擾動法和構造李雅普諾夫(Lyapunov)泛函法,證明了系統的解在有限時間內爆破。 文獻[20]研究了以下具有聲學邊界條件的擬線性波動方程,證明了在初始能量為負的情形下解的整體不存在性: 受以上這些文獻的啟發,本文在文獻[20]的基礎上,在聲學邊界上有源項時,研究邊界源項對解的影響,并最終得出解的整體不存在性。 引入空間 固定T>0,定義能量泛函如下: (2) 引理1 若(u,z)為方程(1)的解,則由式(2)定義的能量泛函E(t)滿足: (3) 證明用ut乘以方程(1)中第1個式子并在Ω上積分,易得式(3)。引理1證畢。 利用文獻[14-18]中的方法,可以證明方程(1)有局部解存在性,結果如下: 定理2 假設α,β,m,p,l≥2,max{β,m}≤α E(0)<0, (4) 則方程(1)的解(u,y)∈Z×L2([0,T);L2(Γ1))在有限時間內爆破。 證明令H(t)=-E(t),則由式(2)~式(4)可得: (5) 構造Lyapunov泛函: (6) (7) 其中:M,j1,j2,j3的取值范圍將在后面給出。 首先估計L′(t),對式(6)求導可得: (8) 利用H?lder不等式和Young不等式可得: (9) (10) (11) 將式(9)~式(11)代入式(8)中可得: (12) 選擇合適的μ,δ,η滿足: 代入式(12)可得: (13) (14) 由式(5)、Poincaré不等式、Young不等式和max{2,β,m}≤α可得: (15) (16) (17) (18) 可得: 同理: (19) 其中:c為廣義常數;取α<θ (20) (21) 其中:r為一正常數。 上述估計意味著: (22) 一方面,由H?lder不等式和α>2得: 這個不等式表示存在常數c>0,使得: 再利用Young不等式可得估計: 由式(5)、式(7)和式(18)可得估計: (23) 故有: (24) 另一方面,由h(x)、q(x)本性有界、H?lder不等式、α≥2及Poincaré不等式可得: 這意味著: 利用Young不等式可得: 將式(23)代入上式可得: (25) 將式(24)、式(25)代入式(22)可得估計: (26) 由式(21)和式(26)可得: (27) 式(27)在(0,t)上積分可得: (28)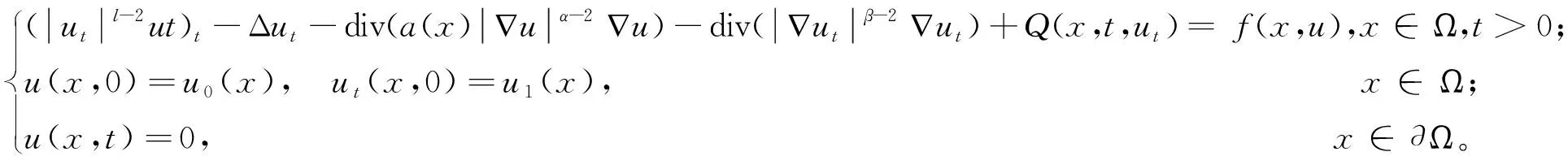
1 預備知識
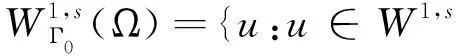
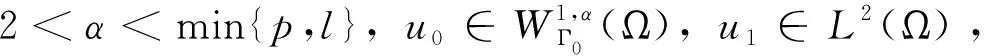
2 解的整體不存在性