齒面摩擦對兩級五分支行星齒輪系統分岔特性的影響

董 皓，張顥秦，張建文

(西安工業大學 機電工程學院，陜西 西安 710021)

0 引言

兩級行星傳動具有承載能力強、結構緊湊、傳動比大、傳動效率高等優點，廣泛應用于汽車、礦山開采、航空、船舶等各個領域，但行星齒輪裝置傳動構件多、動態耦合復雜，運轉過程中的振動產生過大的動載荷和噪聲，制約了其發展和應用，因此，研究齒面摩擦對行星齒輪非線性動態特性的影響顯得尤為重要。

諸多學者針對含摩擦力的齒輪非線性動力學模型的研究做了大量的工作。Ambarisha等[1]利用集中參數法和有限元法分別建立了圓柱直齒的行星齒輪傳動模型，發現了該模型具有復雜的非線性動力學特性，包括跳躍、混沌運動和倍周期分岔等；Kahraman[2]建立了三維單級行星齒輪的動力學模型，可以用來模擬和分析系統固有頻率和強迫振動響應；Li等[3]基于純扭轉非線性動力學模型，分析了包括嚙合阻尼和激勵頻率在內的工作參數對系統混沌和分岔特性的影響；劉志宇等[4]針對齒輪副6自由度多間隙彎扭耦合非線性振動模型，研究了隨轉速、間隙變化時，齒面摩擦對行星齒輪傳動系統分岔特性的影響；毛君等[5]通過分析相平面圖和龐加萊截面研究了嚙合剛度、阻尼比及激振頻率對齒輪系統動態特性的影響；李晟[6]綜合運用分岔圖、相空間軌線和Poincáre截面研究了激勵頻率、嚙合阻尼比對系統分岔與混沌特性的影響；向玲等[7]研究了風電齒輪箱兩級行星齒輪傳動系統的非線性動力學特性；陳甫等[8]綜合考慮了齒側間隙、齒面摩擦和時變嚙合剛度等非線性因素對系統通往混沌的過程進行了研究；王靖岳等[9]研究了干摩擦對行星齒輪傳動系統分岔特性的影響；陸鳳霞等[10]通過數值積分方法分析了16自由度人字齒輪副彎-扭-軸耦合的非線性動力學模型的嚙合力、時變摩擦力和摩擦力矩，比較了有無考慮齒面摩擦時系統的周期振動時域響應、振動位移分岔圖及最大Lyapunov指數變化圖；高楠[11]以風力發電機多級齒輪傳動系統為研究對象，對內外激勵參數變化下系統的運動穩定性、分岔特性分析以及嚙合狀態分析等進行了研究；董皓等[12]建立了基于變形協調條件的行星齒輪傳動系統的靜態均載力學模型，研究了系統的均載特性；盛冬平[13]圍繞直升機主減速器兩級行星傳動系統的動力學特性展開研究。

綜上所述，對齒面摩擦影響下兩級五分支行星系統的分岔特性研究較少。本文綜合考慮了齒面摩擦、時變嚙合剛度及齒側間隙等非線性因素，建立了系統非線性動力學模型，并利用數值積分方法進行求解，研究了齒面摩擦影響下系統隨轉速、間隙等參數變化下的分岔特性。

1 系統非線性動力學模型

圖1為兩級五分支行星傳動系統結構示意圖，其中輸入扭矩Tin作用在第Ⅰ級太陽輪的輸入軸上，負載扭矩Tout作用在第Ⅱ級的行星架輸出軸上，Ⅰ級行星架c(I)與Ⅱ級太陽輪s(Ⅱ)裝配在一起，具有較大的扭轉剛度Kc1s2，p代表行星輪，r代表內齒圈。

假定內齒圈固定，行星輪具有足夠大的支撐剛度，因此不計行星輪與內齒圈的彎曲變形，圖2為兩級五分支行星傳動系統的動力學模型。

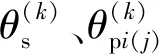
圖2 兩級五分支行星傳動系統的動力學模型Fig.2 Dynamic model of a two-stage five-branch planetary transmission system

各構件的制造誤差在內、外嚙合線上的當量累積綜合嚙合誤差可表示為

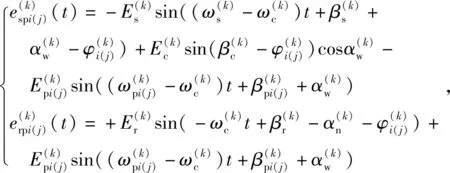
(1)

系統的齒側間隙和支撐間隙函數可表示為

(2)

(3)

(4)

圖3 齒輪副的時變嚙合剛度Fig.3 Time varying meshing stiffness of gear pair

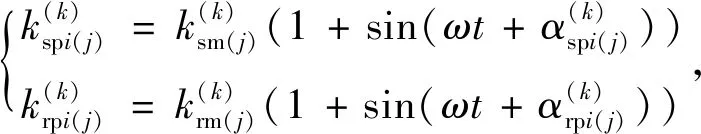
(5)

外、內嚙合阻尼系數表達式為

(6)

2 系統各齒輪副齒面摩擦計算

根據系統的嚙合受力分析，計算了兩級行星輪系的摩擦力臂，l=1,2表示嚙合對1，嚙合對2。

定義太陽輪與行星輪、內齒圈與行星輪第l對輪齒嚙合經過時間t后移動的距離為

(7)

由齒輪傳動的幾何關系可知太陽輪與行星輪以及內齒圈與行星輪的摩擦力臂表示為

(8)

相互嚙合接觸齒面在任一位置的相對速度為

(9)

(10)

式中，sgn(·)為符號函數

齒面摩擦力(根據庫侖定律)為

(11)

3 系統微分方程

基于集中參數法，建立系統非線性振動微分方程組，其中Ⅰ級太陽輪微分方程：

(12)

Ⅰ級行星輪微分方程：

(13)

Ⅰ級行星架微分方程：

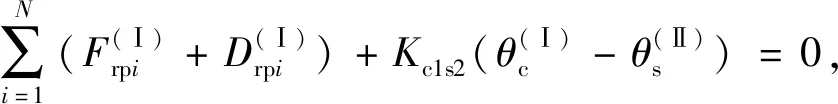
(14)

Ⅱ級太陽輪微分方程：

(15)

Ⅱ級行星輪微分方程：

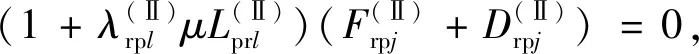
(16)

Ⅱ級行星架微分方程：

(17)

各誤差在內、外嚙合線上產生的無量綱累積綜合嚙合誤差可表示為

(18)

無量綱齒側間隙和支撐間隙可表示為

(19)

同時由于齒側間隙和支撐間隙的存在，使系統包含了剛體位移，方程有不定解，對于扭轉方向需要進行適當的坐標變換，引入相鄰構件之間的相對位移作為系統的廣義坐標如下：

(20)

將式(20)帶入到無量綱化后的振動方程中，可得變換坐標后的Ⅰ級外嚙合微分方程：

(21)

Ⅰ級內嚙合振動方程：

(22)

Ⅱ級外嚙合振動方程：

(23)

Ⅱ級內嚙合微分方程：

(24)

4 各因素對分岔特性影響

給定系統輸入功率為400 kW，輸入轉速為4 500 r/min，各級齒輪模數為5，壓力角為20°，第Ⅰ級太陽輪、行星輪和內齒圈的齒數分別為40、20和80，第Ⅱ級太陽輪、行星輪和內齒圈的齒數分別為60、30和120，各級輪齒制造誤差為10 μm，Ⅰ級各輪支撐剛度均為5×108N·m，Ⅱ級各輪支撐剛度均為1×109N·m，采用4-5階變步長Runge-Kutta數值方法對方程進行求解，分析研究齒面摩擦影響下，無量綱轉速及無量綱齒側間隙對系統的分岔特性的影響規律。

4.1 轉速對系統分岔特性影響

第Ⅰ級和第Ⅱ級外嚙合振動系統在摩擦因數μ分別為0、0.03和0.06時隨無量綱轉速Ω變化的分岔特性如圖4和圖5所示。

從圖4(a)可以看出當1<Ω<1.595，系統先后經歷了穩定的周期二、周期三和周期六運動，當轉速Ω=1.595時系統通過倍周期激變的形式進入到混沌運動。當Ω進一步增加到1.94時，系統又通過倒分岔通過短暫的擬周期運動后回歸到周期六運動，最終穩定在周期三運動。從圖4(b)、圖4(c)可以看出，隨著摩擦因數μ的增大，齒面摩擦在一定程度上加劇了系統的振動，但可以有效地抑制混沌運動，混沌區域逐漸減小甚至會完全消失，同時齒面摩擦會消耗系統的能量，所以將摩擦因數μ控制在0.06～0.10是較為合理的。

圖4 Ⅰ級輪系在不同摩擦因數下隨轉速變化的分岔特性Fig.4 Bifurcation characteristics of Ⅰ-stage gear train changed with rotational speed under different friction coefficients

從圖5(a)中可以看出，通過第Ⅰ級行星輪系的減速增扭，第Ⅱ級輪系的振幅具有一定的增加，但隨無量綱轉速變化時呈現出與第Ⅰ級相似的分岔特性，混沌運動區域主要集中在1.574 8<Ω<1.985范圍內。圖5(b)、圖5(c)顯示了摩擦因數μ分別為0.03和0.06時，第Ⅱ級外嚙合振動系統呈現出的分岔特性。從圖中可以看出，隨著摩擦因數的增加，混沌運動區域的面積逐漸減小，最終系統都由周期六運動通過倒分岔回歸到周期三運動。

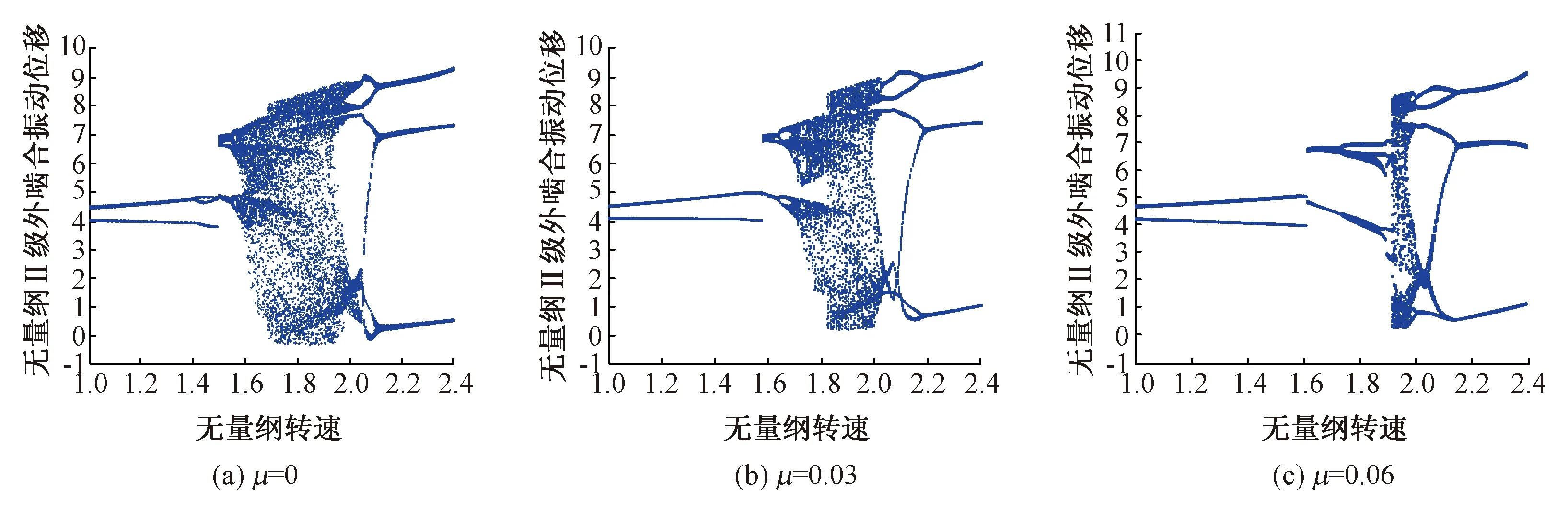
圖5 Ⅱ級輪系在不同摩擦因數下隨轉速變化的分岔特性Fig.5 Bifurcation characteristics of Ⅱ-stage gear train changed with rotational speed under different friction coefficients

4.2 齒側間隙對系統分岔特性影響

圖6 Ⅰ級輪系在不同摩擦因數下隨齒側間隙變化分岔圖Fig.6 Bifurcation diagram of Ⅰ-stage gear train changed with backlash under different friction coefficients

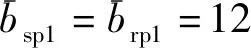
圖8 Ⅱ級輪系在不同摩擦因數下隨間隙變化分岔圖Fig.8 Bifurcation diagram of Ⅱ-stage with backlash under different friction coefficients

圖9中給出了對應的相圖及Poincaré截面圖，可以看出，圖9與圖7具有相似的影響規律。

圖9 第Ⅱ級不同摩擦因數μ的相圖和Poincare圖Fig.9 Phase diagram and Poincare diagram of different friction factor μ in Ⅱ-stage

5 結論

建立了兩級五分支行星輪系的振動微分方程，并采用變步長Runge-Kutta的數值方法進行求解，得到系統隨各參數變化的分岔圖、相圖及Poincare圖，研究了無量綱轉速及齒側間隙等參數對系統分岔特性的影響，所得結論如下：

1)隨著無量綱轉速的增加，無齒面摩擦時系統的敏感振動區域大，混沌特性表現明顯；隨著齒面摩擦的增大，在一定程度上加劇系統的振動及噪音，但由于摩擦消耗系統能量，使得混沌區域寬度越來越窄，系統振動受到抑制。

2)無齒面摩擦時系統在小齒側間隙下都處于穩定的周期運動狀態，隨著齒側間隙的增大使得系統出現強非線性振動，使得系統處于混亂振動狀態，混沌運動表現非常明顯；隨著摩擦因數的增大，齒面摩擦會消耗系統的能量，混沌區域逐漸減小，最終系統回歸到倍周期運動狀態。

3)系統第Ⅰ級與第Ⅱ級在不同參數變化情況下，所表現出來的分岔特性具有一定的相似性。