變截面格構式結構軸壓臨界力的高效分析方法

孟麗霞，于傲群，劉士明

（沈陽建筑大學機械工程學院，遼寧 沈陽 110168）

1 引言

由眾多梁桿組成的復雜格構式結構，廣泛應用于建筑鋼結構、起重機械臂架、輸電塔架以及某些橋梁結構中，其中變截面格構式結構憑借自重輕、材料利用合理、容易實現等強度原則，在工程實際中應用更加廣泛。結構的軸壓穩定性問題明顯區別強度問題，結構失穩破壞由于事發前沒有明顯的征兆，一旦失穩破壞即會對人身安全、社會經濟造成不可逆的損害。因此，許多學者將結構的穩定性分析作為關注的焦點。現階段，采用有限單元法、靜力法等分析等截面實腹式構件以及簡單組合結構的軸壓穩定性問題已相對成熟[1-3]。而相較于等截面梁單元研究，目前變截面梁單元的傳統做法是將其密分成多段等截面梁單元進行模擬，這種方法已經被證明是相當低效的。文獻[4]利用數值計算求解出一種具有軸向力和剪切變形的梁單元精確剛度矩陣。文獻[5]利用有限差分法對變截面懸臂梁單元進行了計算分析。文獻[6]基于Euler-Bernoulli梁理論研究了具有不同截面形狀的變截面梁單元沿長度的慣性矩變換，然后采用Bessel函數，獲得了包括軸向力影響的剛度矩陣。文獻[7]將變截面構件載荷轉換為等效節點載荷，采用增量割線剛度方法，推導出工程中常見截面類型統一表述的新型變截面梁單元。

文獻[8]提出一種TTH彎曲梁柱單元，并計入二階效應影響對變截面工字梁單元進行研究。針對復雜格構式結構或桁架結構的穩定性分析，目前主要采用有限單元法，一個結構進行一次建模，建模工作量大，計算效率不高。為了提高計算準確率和效率，許多學者對格構式結構的穩定性和非線性變形進行了深入的研究[9-13]。其中，在等截面格構式結構研究方面，學者們采用共旋坐標法、弧長法等對其進行了研究[9-10]。在變截面格構式結構研究方面，Theodore G.假設變形曲線，采用加遼金法獲得含有錐形截面的多跨梁與框架結構的失穩臨界力[11]。文獻[12]通過慣性矩等效方式將臂架從格構式結構簡化為實腹式梁結構進行穩定性研究。文獻[13]利用多項式函數進行變截面梁單元的高階計算，采用五次Hermit插值獲得形函數，剛度矩陣具有較精確的表達形式，但其獲得的變截面梁單元光滑連續性不高，并且插值函數階數過高會導致收斂性較差，最終使得求解精確度降低。

使用三次樣條函數構建變截面格構式梁單元位移場，基于非線性有限元法推導計及二階效應的變截面格構式梁單元的切線剛度矩陣，結合靜力凝聚法獲得一種新型的兩節點梁單元，利用該單元對由梁桿組成的變截面格構式結構的軸壓穩定性進行分析。

2 三次樣條變截面梁單元位移場

變截面格構式梁單元，如圖1所示。單元長度為l，在任意截面x處的截面慣性矩I(x)、面積A(x)與原點o處的截面慣性矩I0、面積A0的關系為：

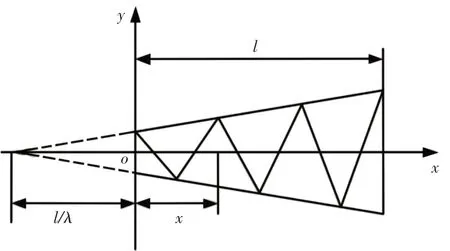
圖1 變截面格構式梁單元Fig.1 The Lattice Beam Element with Variable Section

利用三次樣條插值推導變截面梁單元切線剛度陣時，對梁單元進行基本假定：

（1）梁單元變形時，單元橫截面與變形前保持一致；

（2）遵循廣義Hooke定律，單元材料為各向同性；

（3）梁單元橫截面在變形后仍垂直于法線。

通過以上假定得到函數形式：

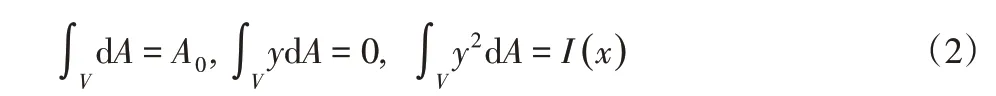
式中：λ—變截面構件錐度的無量綱參數，λ＞-1。

圖2 三次樣條變截面格構式梁單元描述Fig.2 Cubic Spline Description of Variable Section Lattice Beam Element

根據三次樣條插值定理，由于梁單元樣條曲線等分為3份，每份樣條曲線的橫向位移場均可表示為三次多項式，并且多項式參數是由節點的邊界條件和單元變形的連續條件決定的，如下所示。

式中：ξ=x/l。結合上述條件，獲得變截面格構式梁單元的橫向位移場形函數向量：

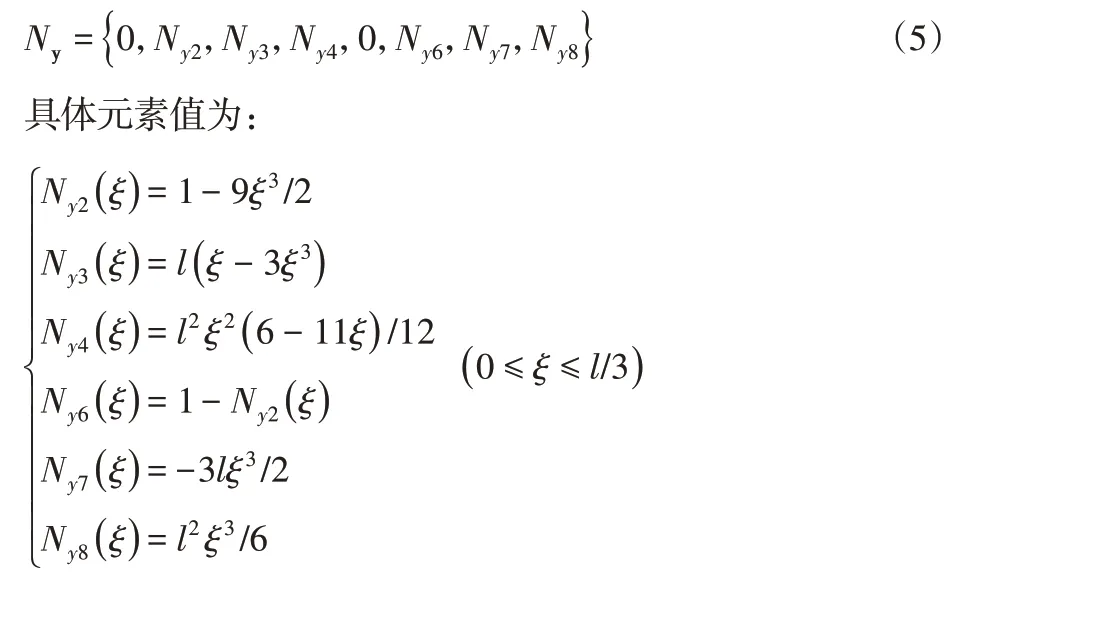
式（6）兩側同時對y取積分得：

3 變截面梁單元切線剛度矩陣

在大位移大轉角小應變條件下，忽略格林應變中與縱向位移相關的高階項得：

其中各變量的具體表達式詳見附錄。當剛度矩陣式（17）中錐度系數λ→0且軸力P→0時，所得的變截面梁單元剛度矩陣KT即可轉化成傳統等截面梁單元剛度矩陣K′T：

4 算例分析

選取無量綱穩定系數mcr=pcrl2/(EI2)，分析該懸臂變截面格構式構件的整體穩定性。采用本文新型變截面格構式梁單元，將構件劃分為一個單元，得到對應剛度矩陣：

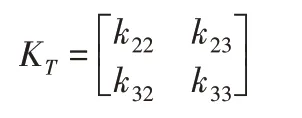
由結構失穩臨界力方程Det[KT]=0，獲得軸壓失穩臨界力，進而可得穩定系數mcr，并與文獻[14]的理論精確解進行對比，對比結果，如表1所示。

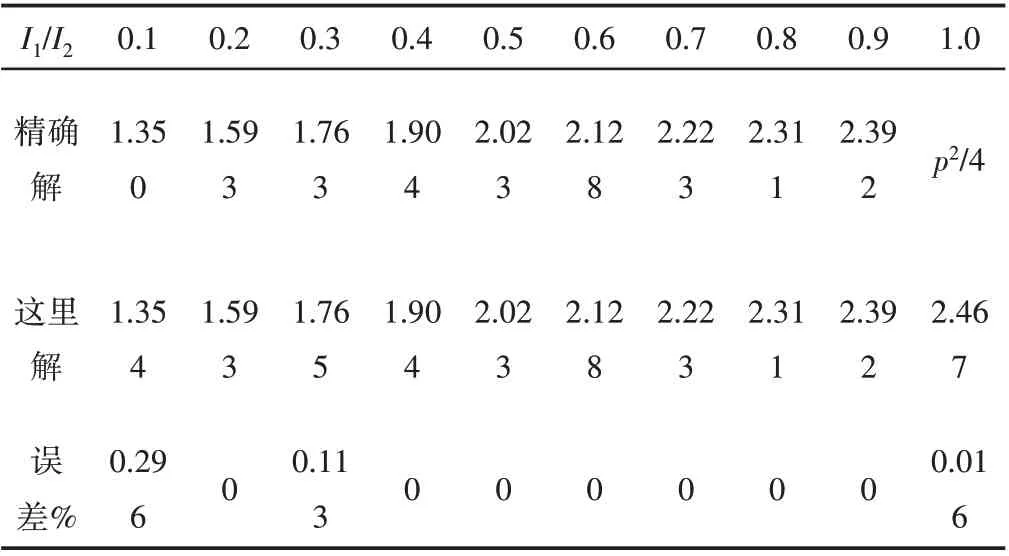
表1 懸臂格構式構件穩定系數mcr計算比較Tab.1 Comparison of Stability Coefficients mcr of Cantilever Lattice Structure

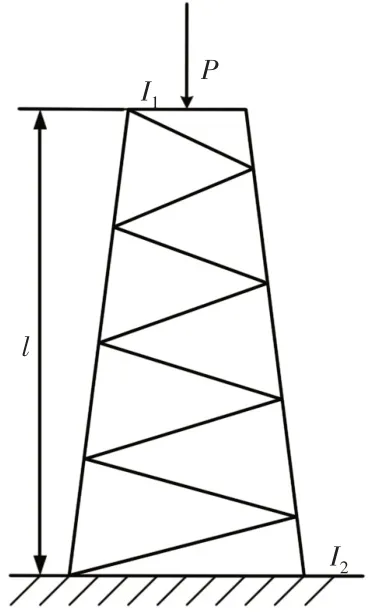
圖3 懸臂變截面格構式構件Fig.3 Cantilever Variable Section Lattice Structure

將該組合構件中每個變截面段劃分為一個單元，其中變截面單元1和3利用這里獲得的新型梁單元剛度陣進行計算，等截面單元2利用這里剛度陣令λ=0退化得到的等截面梁單元剛度陣進行計算。通過剛度矩陣組裝集成求解可得到該梭形構件的失穩臨界力。計算出不同I1/I2和x/l情況下的mcr值，這里結果與文[14]理論結果對比，如表2所示。

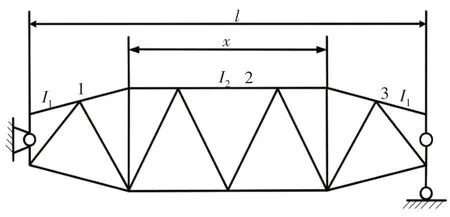
圖4 簡支梭形格構式組合構件Fig.4 The Combined Spindle Lattice Structure with Simple Support

表2 梭形格構式構件穩定系數mcr計算比較Tab.2 Comparison of the Stability Coefficient mcr of the Combined Spindle Lattice Structure

由表1、表2結果可見，這里所推導的變截面格構式梁單元切線剛度矩陣在進行結構的穩定性分析時，具有非常高的計算精度。本文獲得的新型梁單元不僅可用于單構件軸壓穩定性分析，也可用于變截面、等截面組合構件的軸壓穩定性分析。同時，所形成的整體剛度陣與傳統兩節點梁單元具有相同的階數，可以方便實現變截面梁到等截面梁的轉化。

5 結論

（1）基于有限元插值理論，采用三次樣條插值推導變截面格構式梁單元的切線剛度矩陣，隨后結合靜力凝聚法消除單元節點的曲率自由度，推導出一種新型的變截面格構式梁單元；（2）利用推導的變截面格構式梁單元剛度矩陣對變截面格構式懸臂結構和簡支梭形格構式組合結構進行軸壓穩定性分析，計算結果與Timoshenko精確解幾近相同，表明這里方法可高效地分析由梁桿組成的復雜變截面格構式結構的穩定性問題；（3）這里凝聚后的變截面梁單元剛度陣與傳統有限元法所得梁單元剛度陣的階數保持一致，可與傳統梁單元剛度陣集成組裝，方便統一分析求解；且當λ趨于0時，這里剛度陣可退化為計及二階效應的等截面梁單元剛度陣。

附錄：