加工及裝配誤差對氣體軸承運動狀態的影響規律*

李勇德 何永熹 劉檢華

(北京理工大學機械與車輛學院 北京 100081)

氣體軸承具有摩阻極低、轉速高以及環境適應性好等優點，在高速旋轉機械中獲得了廣泛應用[1-2]。氣體軸承具有多種類型，其中動靜壓氣體軸承具有啟動特性好、不易磨損、穩定性高等特點[3-5]。氣體軸承間隙很小，有較高的加工、裝配精度要求[6]。在旋轉機械中，不對中是導致轉子失穩的重要原因，而加工與裝配誤差則是造成軸承不對中的主要因素[7]。

針對加工與裝配誤差對氣體軸承性能的影響，國內外多位學者進行了相關研究。任天明等[8]研究了加工誤差對H型動壓氣體軸承剛度的影響，結果表明，0.2 μm的氣膜誤差會導致氣膜剛度降低20%以上。邊新孝等[9]研究了加工誤差對氣體靜壓軸承承載能力的影響，發現軸承間隙誤差為平均氣膜間隙的5%時，承載力可產生約10%的變化。姚英學等[10]利用相容性變換條件，研究了制造誤差對氣體承靜態特性的影響，發現誤差對氣體軸承徑向承載能力影響較大。PANDE等[11]基于二維可壓縮黏性流的Reynolds方程計算了表面粗糙形貌對靜壓軸承靜態特性的影響。STOUT[12]采用類似的數值分析方法研究了軸承間隙等制造誤差對軸承靜態特性的影響。CROSBY[13]分析了靜壓軸承靜態特性受橢圓圓度誤差與表面粗糙度的影響規律。趙琪等人[14]研究了制造誤差造成的軸頸偏斜對軸承性能的影響，發現軸頸偏斜距離變化對軸承性能影響較大，偏斜角度對軸承性能影響較小。但現階段所做的加工與裝配誤差對氣體軸承運動狀態影響的研究多采用以Reynolds潤滑方程為基礎的數值分析方法，對分析動靜壓耦合效應誤差較大[15]，并且大都為對軸承穩態特性的求解，而對軸承的動態特性問題涉及較少。賈晨輝等[16]采用商業軟件FLUENT研究了動靜壓氣體軸承的運動狀態隨轉速變化的規律，發現轉子的振動幅度隨轉速的增加呈現先減小后增大的狀態，并指出由于氣體軸承轉速極高，軸承氣膜的變化是非線性過程，因此以氣膜為研究對象是研究氣體軸承穩定性的關鍵。

本文作者以螺旋槽動靜壓氣體軸承氣膜為研究對象，基于計算流體力學與六自由度耦合方法，采用流體仿真軟件FLUENT模擬轉子在運轉過程中的軸心軌跡，通過分析軸心軌跡及其頻譜特征，研究加工和裝配誤差對動靜壓氣體軸承運動狀態的影響規律。研究結果為動靜壓氣體軸承設計、加工與裝配精度的確定提供理論依據。

1 氣膜模型

1.1 球面螺旋槽動靜壓氣體軸承結構

球面螺旋槽動靜壓氣體軸承的結構簡圖如圖1(a)所示，主要由兩部分組成：帶有螺旋槽的轉子以及帶有供氣孔的定子。為了簡化計算，建立的氣膜模型如圖1(b)所示，尺寸參數如表1所示。

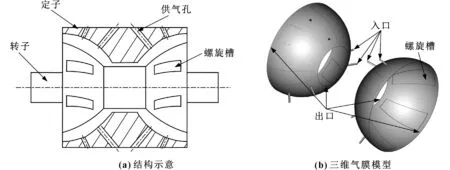
圖1 球面螺旋槽動靜壓氣體軸承Fig 1 A hybrid bearing with spherical spiral grooves (a)the schematicof structure;(b)three-dimensional model of the gas film

1.2 網格劃分與邊界條件

由于氣體軸承氣膜厚度很薄，并且需要考慮到由制造、裝配誤差產生的細微尺寸變化，故采用網格劃分軟件Pointwise對氣膜模型進行網格劃分。Pointwise具有極高的尺寸識別以及擬合精度，對于處理復雜細小尺寸幾何模型具有獨特優勢。為檢驗所用網格分辨率得到的仿真結果的收斂性，對無加工及裝配誤差的理想模型進行網格無關性檢驗，測試網格總量分別為90萬、120萬與150萬，網格劃分如圖2所示。其中對無供氣孔區域實施結構化網格剖分，對供氣孔與氣膜交接處實施六面體與四面體混合網格剖分。圖3所示為3種不同網格分辨率下的幅頻圖。結果表明，隨著網格分辨率的提高，軸心軌跡幅值差異在減小，而且120萬網格分辨率得到的軸心軌跡幅值相較于150萬得到的結果差異已經很小。綜合考慮計算精度與計算成本，文中后續仿真均采用網格總量約為120萬的分辨率進行模型計算。

圖2 氣膜網格劃分示意Fig 2 Mesh of the gas film of the hybrid bearing

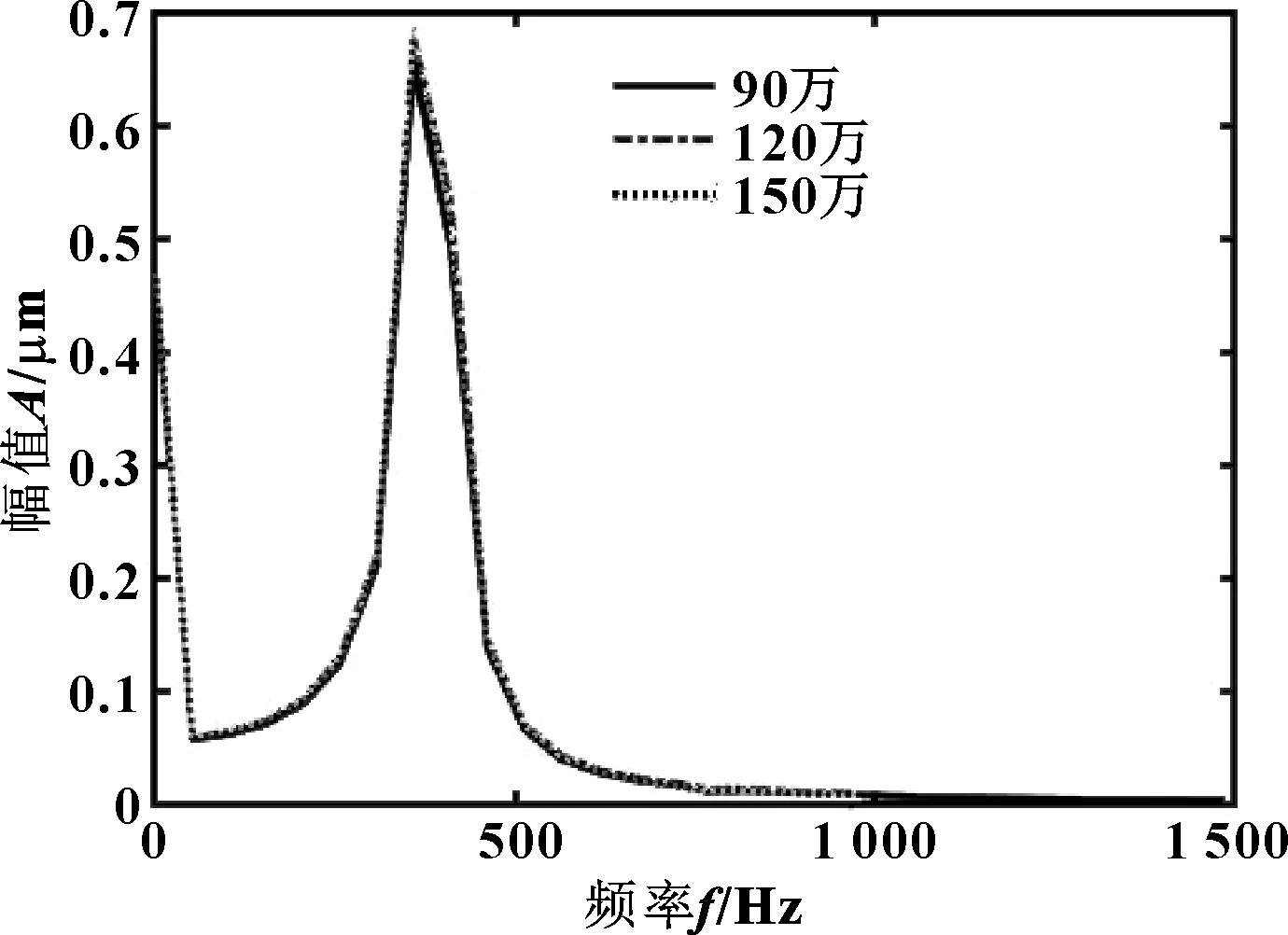
圖3 不同網格分辨率下的軸心運動軌跡幅頻圖Fig 3 Amplitude-frequency graph of the axis orbitfor three different grid resolutions

對氣體軸承進行瞬態流體動力學仿真時的邊界條件為：(1)軸承兩端氣膜的大端口與小端口均為出氣口，并且出氣口處氣壓為101.3 kPa(1個大氣壓)；(2)供氣孔端面為壓力進口，供氣壓力為穩定的0.2 MPa，氣體為氦氣，黏度為2×10-5Pa·s，且考慮為可壓縮流體；(3)其余邊界條件為壁面邊界條件，其中內壁面為旋轉的剛性壁面，外壁面為固定壁面。

1.3 流體潤滑理論

對螺旋槽動靜壓氣體軸承動態特性的仿真過程中，其流體模型主要考慮連續性方程以及動量守恒方程，由于潤滑氣體在流動過程中氣體能量交換較小，故不考慮能量守恒。另外，由于氣體在軸承氣膜內存在較大的壓力變化，需要考慮氣體的可壓縮性，故為使模型方程封閉，還需要引入氣體狀態方程。

氣體軸承的模型域內無質量源項，其非穩態連續性方程為

(1)

式中：ρ為流體密度；t為流體流動時間；u為流體矢量場。

針對文中研究的氣體軸承，其流體為氦氣，可以考慮為牛頓流體，且重力作用對氣膜內流體的運動影響很小，可以忽略。采用FLUENT中k-εRealizable湍流模型計算氣膜流動，其動量方程與湍動能方程為

(2)

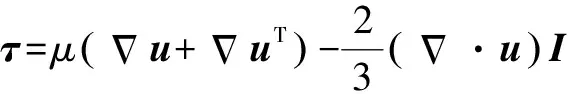
另外，邊界層選擇FLUENT中的標準邊界層函數。

對于完全氣體，其3個基本狀態參數壓力p、密度ρ和溫度T滿足狀態方程：

p=ρRT

(3)

式中：T為絕對溫度；R為氣體常數。

1.4 6DOF理論

工程中可根據物體的運動狀態將問題分為2種，一種是運動狀態已知的問題，稱之為主動運動，另一種是運動狀態未知的被動運動。在氣體軸承中轉子運動，既受到電磁力矩作用，又受到周圍氣體的作用，而文中關心的轉子的質心運動主要受周圍氣體的作用力的影響，而轉子的運動又會影響到氣膜結構，進而影響氣膜內的流體運動，因此這是一個雙向耦合問題，也是被動運動問題。FLUENT中的6DOF(六自由度)模型主要用于模擬計算域中存在運動的剛體的流固耦合問題。

慣性坐標系下剛體結構的重心平移運動的控制方程為

(4)

式中：v為質心的平移速度矢量；m為物體質量；fG為周圍流體作用在剛體界面上的外力矢量。

在體坐標系下剛體旋轉運動的控制方程為

(5)

式中:ωB為剛體在體坐標系下旋轉運動的角速度矢量；L為慣性張量；MB為剛體的力矩矢量。

將以慣性坐標系表達的MG轉化為以體坐標系表達，形式如下：

MB=RMG

(6)

其中變換矩陣：

(7)

式中:Cχ=cosχ，Sχ=sinχ，χ為θ、φ、ψ；角θ、φ、ψ分別為繞x、y、z軸旋轉的歐拉角。

另外，慣性坐標系中，剛體受到的周圍流體合力矩：MG=∑r×fG。

2 仿真結果與討論

文中分別對球面螺旋槽動靜壓氣體軸承為理想狀態(無加工與裝配誤差)，定子存在對中誤差，以及定子存在尺寸誤差等幾種不同情況下的轉子軸心軌跡的動態行為進行分析。

2.1 理想狀態分析

在無加工與裝配誤差的理想情況下，不同轉速下轉子軸心軌跡圖和頻譜圖分別如圖4、圖5所示。當轉速為10 000 r/min時軸心軌跡由大到小逐漸穩定在較小的橢圓范圍內，振幅最高時為0.014 μm(見圖4(a)、圖5(a))。當轉速為20 000 r/min時軸心軌跡依舊由大到小穩定在較小的橢圓范圍內，但橢圓長短軸長度有所提升，振幅最高時為0.038 μm(見圖4(b)、圖5(b))。當轉速為30 000 r/min時軸心軌跡一直穩定在較大的橢圓范圍內，振幅最高時為0.087 μm(見圖4(c)、圖5(c))。當轉速為40 000 r/min時軸心軌跡發散，轉子不能達到穩定狀態(見圖4(d)、圖5(d))。

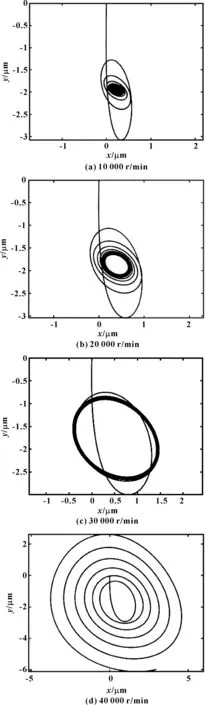
圖4 不同轉速下轉子軸心軌跡圖Fig 4 Axis orbits of rotor at revolving speed of 10 000r/min(a),20 000 r/min(b),30 000 r/min(c) and 40 000 r/min(d)

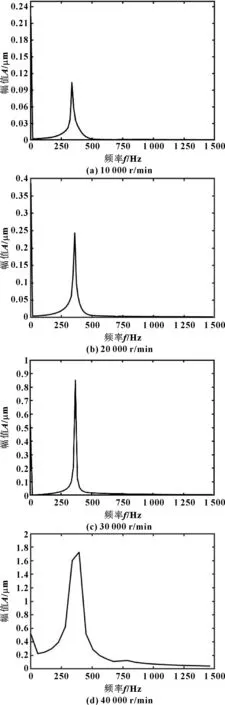
圖5 不同轉速下轉子頻譜圖Fig 5 Spectrograms of rotor at revolving speed of 10 000r/min(a),20 000 r/min(b),30 000 r/min(c) and 40 000 r/min(d)

圖6所示為轉子振幅隨轉速的變化關系，可以看出，隨著轉子轉速增加，轉子振幅逐漸增大。另外，從圖4可以看出，隨著轉子轉速增加，軸心軌跡從穩定在較小的橢圓軌跡中演變為較大的橢圓軌跡，隨著轉速繼續上升軸心軌跡發散；當轉速在臨界轉速30 000 r/min時，軸承運行狀態穩定，軸心軌跡為規則的橢圓形，當轉速達到40 000 r/min時，軸承穩定狀態被破壞，軸心軌跡發散，軸承處于失穩狀態。文獻[17]針對氣體軸承轉子動力學分析得到了類似的結論，雖然具體結構和轉速有所差異，但是所得轉子軸心軌跡隨轉速的變化規律是一致的。

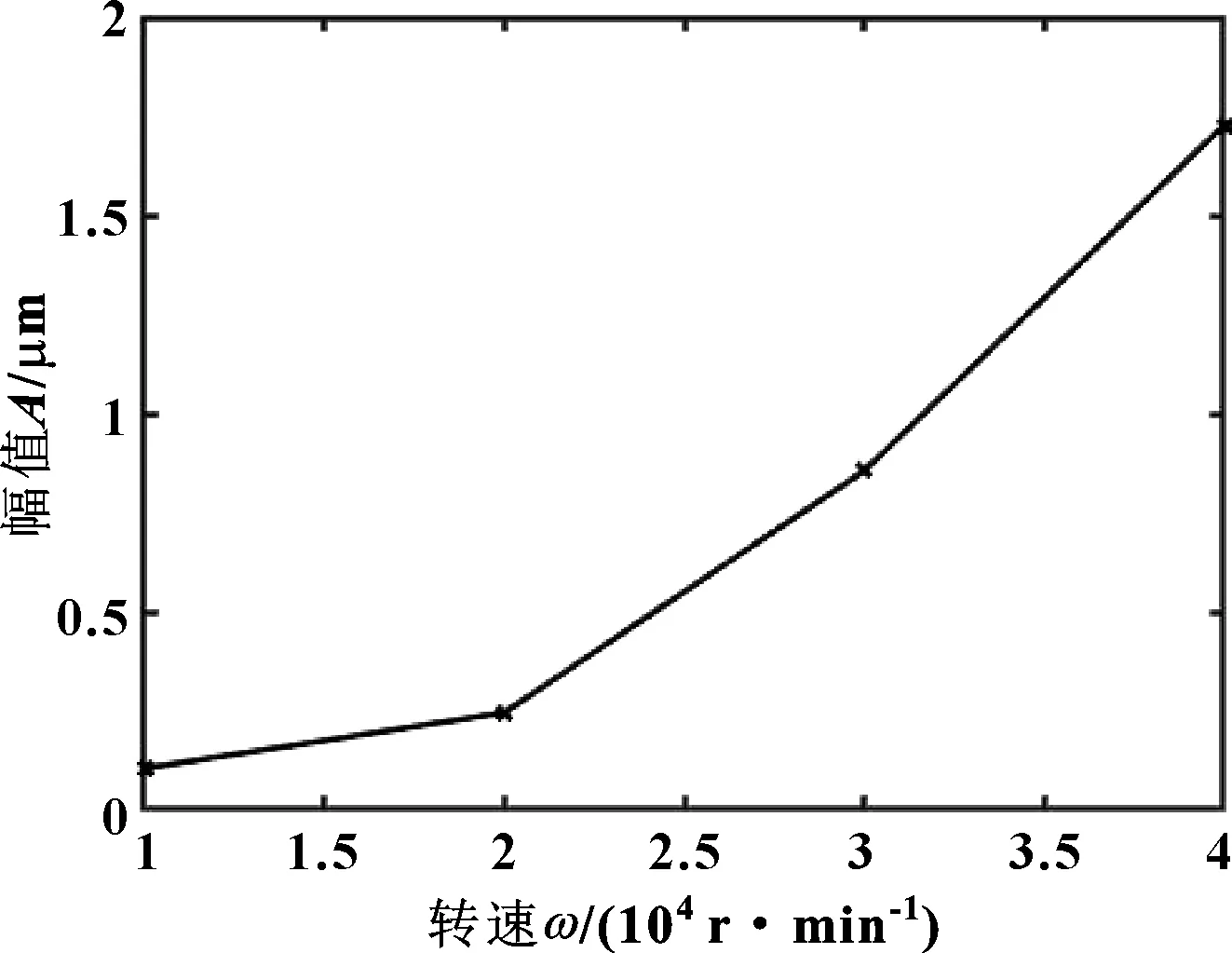
圖6 無誤差時轉子轉速-幅值曲線Fig 6 Rotor revolving speed-amplituderesponse curves without error

2.2 定子軸線偏移

軸承裝配過程中，由于定子兩端球殼軸線不對中，一端定子軸線出現偏移，造成兩端定子裝配出現同軸度誤差，如圖7所示。

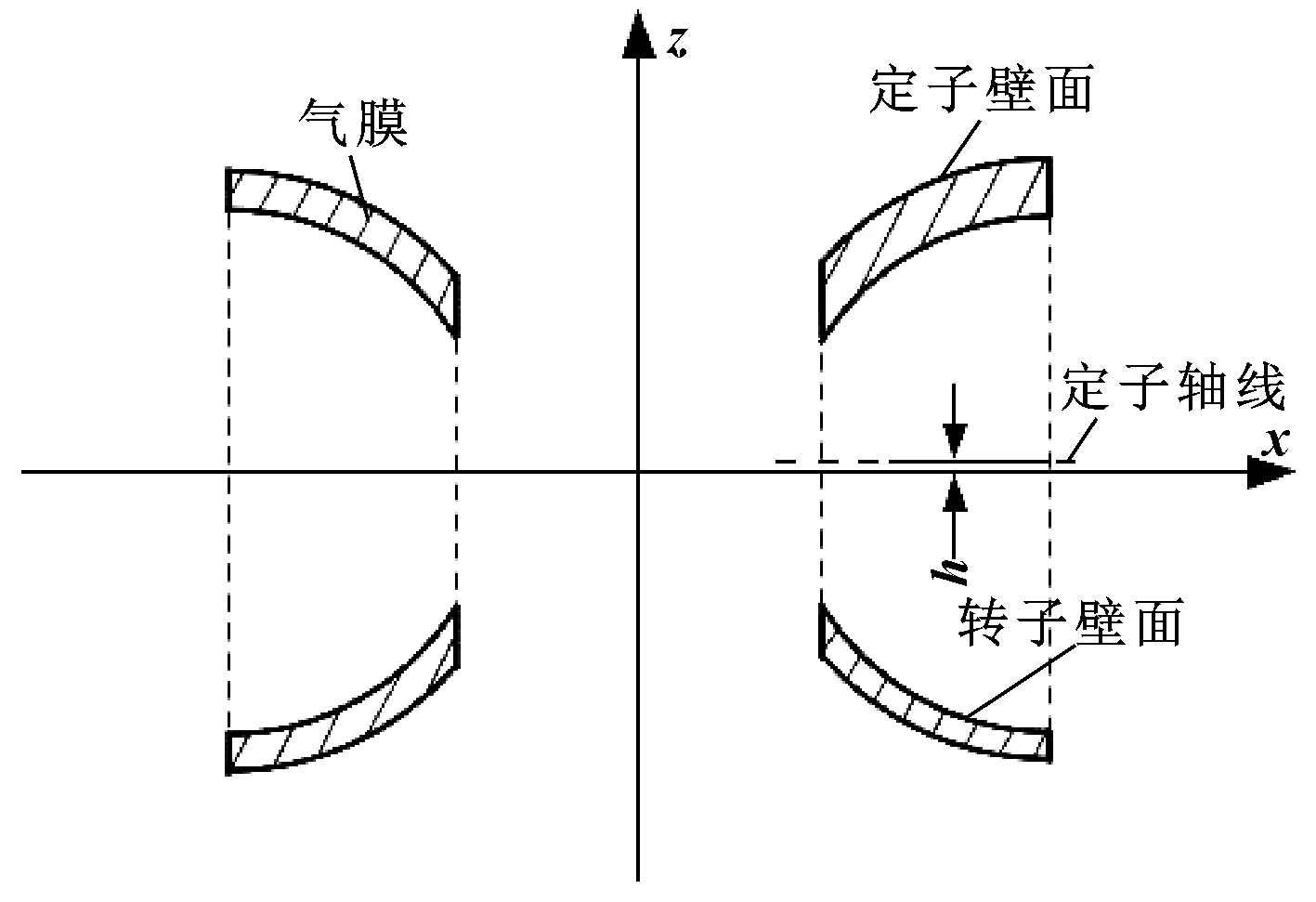
圖7 軸線偏移誤差模型Fig 7 Error model of axis offset

選取轉速為10 000 、20 000、30 000 r/min，在軸線偏移距離h分別為0.5、1、2 μm情況下進行模擬仿真，得到其軸心運動軌跡，并提取頻譜成分分析后，得到不同轉速、不同偏移距離下的轉子振幅變化，如圖8(a)所示。可以看出：定子軸線偏移引起的轉子幅值變化在低轉速的情況下較小，軸承處于穩定運轉的狀態；當轉子速度達到臨界速度30 000 r/min時，轉子振幅受定子軸線偏移影響較大；隨著偏移誤差增加，軸心軌跡從穩定在較小的橢圓軌跡到較大的橢圓軌跡再到極限環運動，如圖8(b)所示，同時軸心軌跡中心點也隨著偏移誤差的出現向y軸負向偏移。

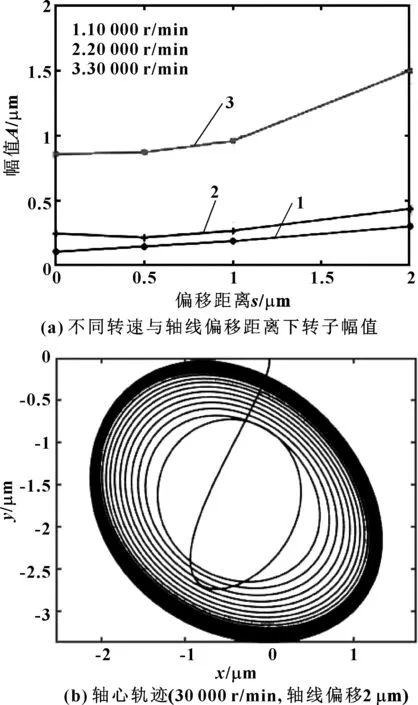
圖8 轉子幅值隨軸線偏移距離變化及轉子軸心軌跡Fig 8 Variation of the amplitude of rotor with axis offset androtor axis orbit (a)amplitude under different speedsand axis offsets;(b)axis orbit (30 000 r/min,axis offset 2 μm)

2.3 定子軸線傾斜

軸承裝配過程中，由于定子兩端球殼軸線不對中，一端定子軸線出現傾斜，造成兩端定子裝配出現同軸度誤差，如圖9所示。

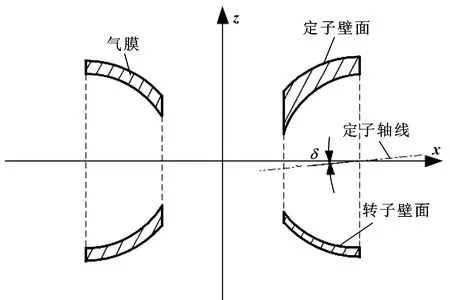
圖9 軸線傾斜誤差模型Fig 9 Error model of axis tilt

選取轉速為10 000、20 000、30 000 r/min，在傾斜角度δ分別為0.5°、1°、2°情況下進行模擬仿真，得到其軸心運動軌跡，通過提取頻譜成分分析，得到不同轉速、不同傾斜角度下轉子振幅的變化，如圖10(a)所示。可以看出：定子軸線傾斜引起的幅值變化規律與軸線偏移類似，在低轉速情況下影響較小；當轉子速度達到臨界速度30 000 r/min時，轉子振幅受定子軸線傾斜影響較大。隨著傾斜誤差增加，軸心軌跡也是從穩定在較小的橢圓軌跡演變為極限環，如圖10(b)所示，同時軸心軌跡中心點也隨著偏移誤差的出現向x軸正向偏移。

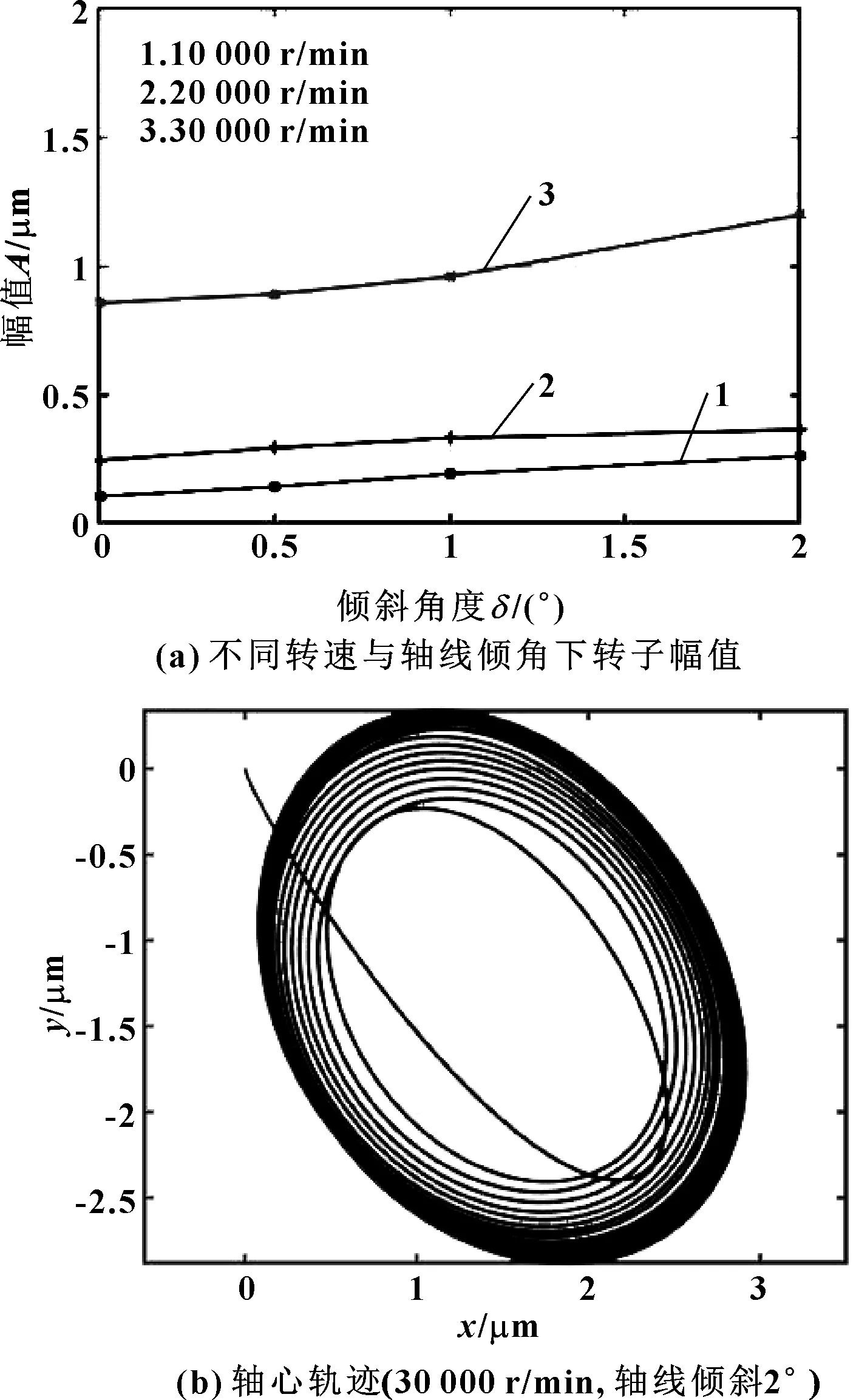
圖10 轉子幅值隨軸線傾斜角度變化及轉子軸心軌跡Fig 10 Variation of the amplitude of rotor with the tilting angleof the axis and rotor axis orbit (a) amplitude underdifferent speeds and tilting angle of the axis;(b)axis orbit (30 000 r/min,tilting angle 2°)

2.4 定子尺寸誤差

軸承加工過程中，由于兩端定子尺寸存在加工誤差，導致兩端氣膜厚度不一致，如圖11所示。

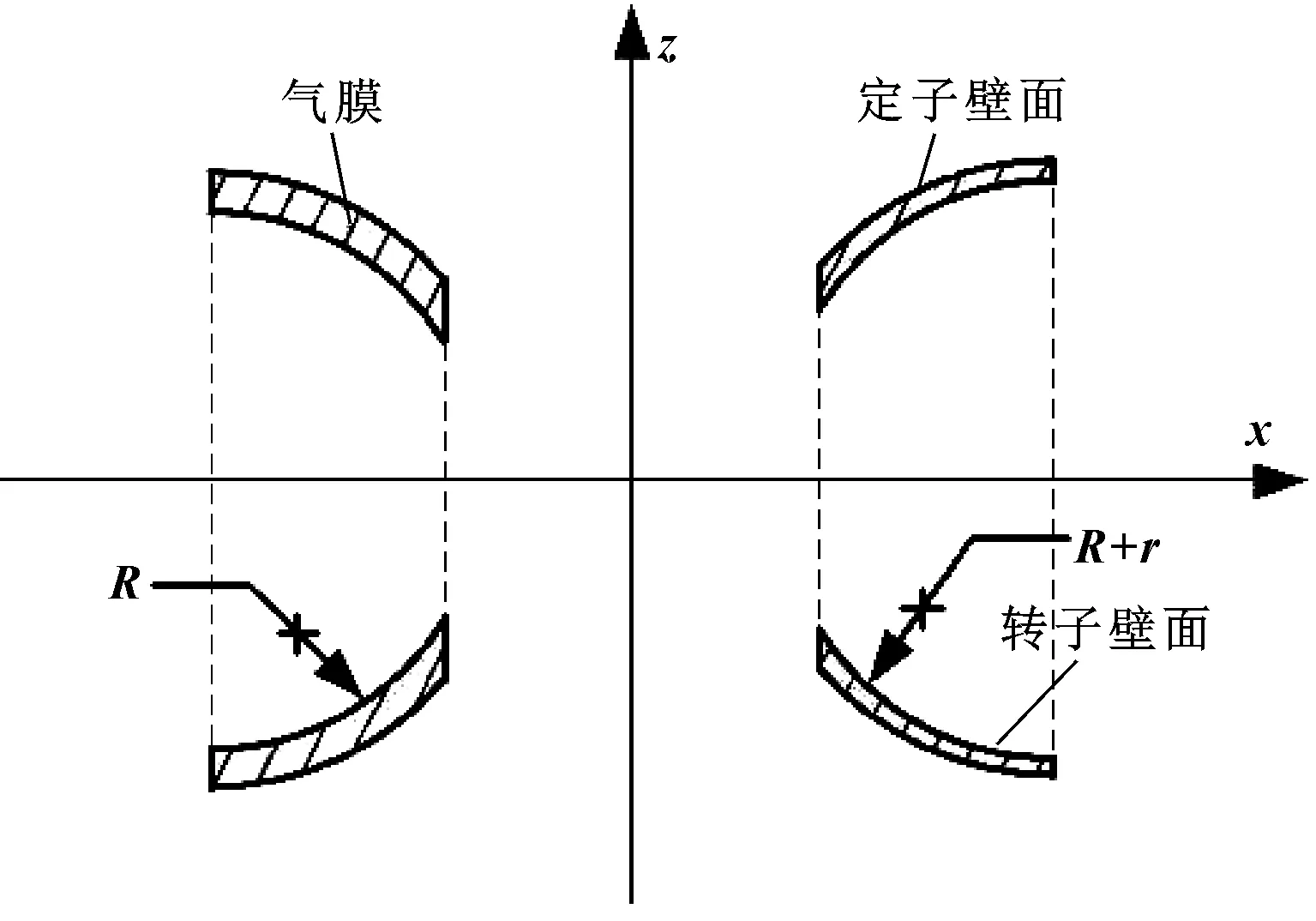
圖11 定子尺寸誤差模型Fig 11 Error model of stator dimension

選取轉速為10 000、20 000、30 000 r/min時，在定子尺寸誤差r分別為0.5、1、2 μm情況下進行模擬仿真，得到其軸心運動軌跡，并提取頻譜成分分析后，得到不同轉速、不同定子半徑誤差下的轉子振幅變化，如圖12(a)所示。可以看出：雖然存在定子半徑誤差，但由于單邊氣膜厚度仍然均勻，所以在所選轉速范圍以及尺寸誤差范圍內，轉子振幅隨著定子半徑誤差的增大僅發生小幅增大，對運動穩定性影響很小。只有當轉速達到30 000 r/min，并且定子半徑誤差達到2 μm時轉子振幅會有一定的提升，但軸心軌跡仍穩定在一定的橢圓范圍內，如圖12(b)所示。

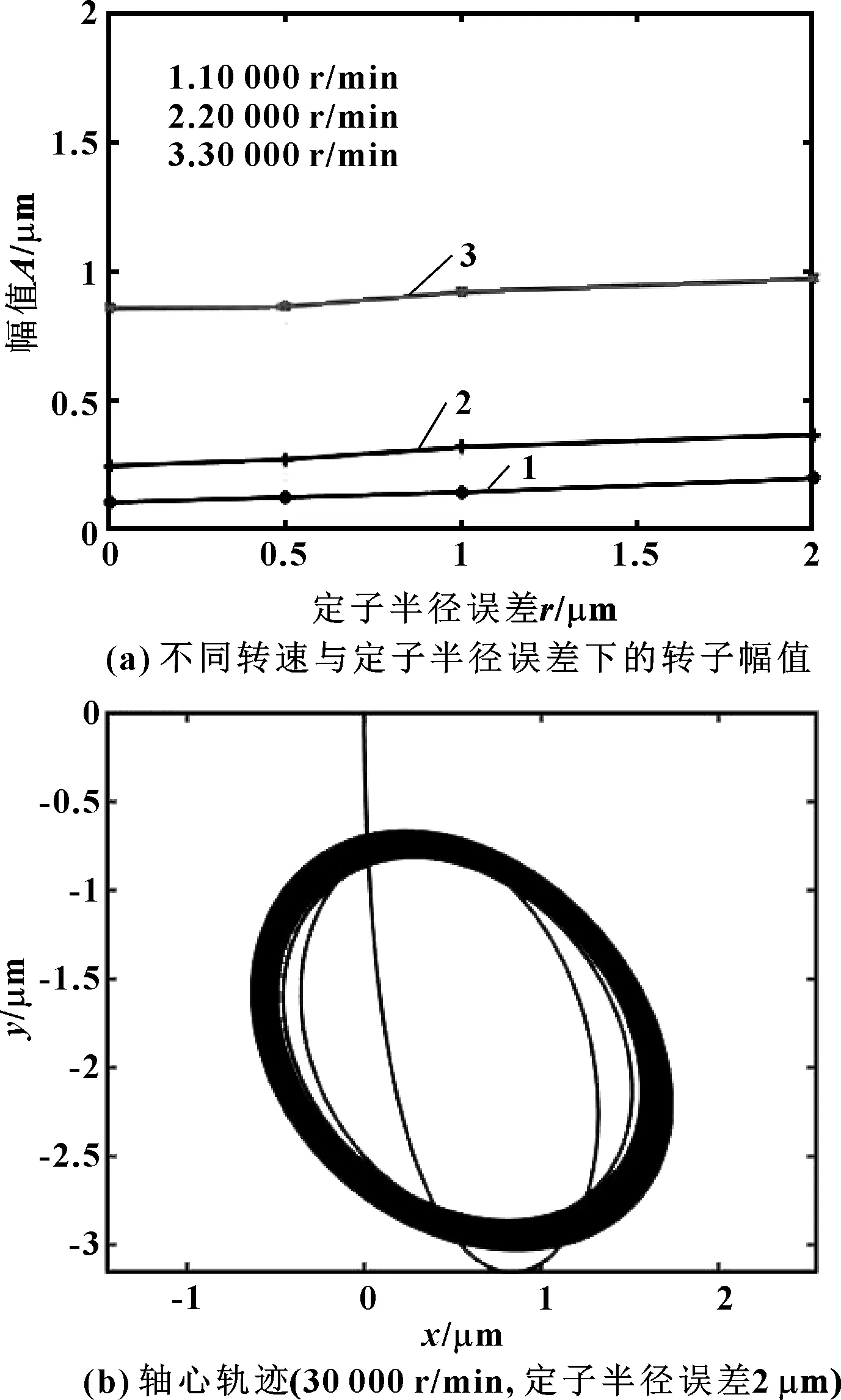
圖12 轉子幅值隨定子半徑加工誤差變化及轉子軸心軌跡Fig 12 Variation of the amplitude of rotor with the radial errorand rotor axis orbit (a)amplitude under differentspeeds and radial errors;(b)axis orbit(30 000 r/min,radial error 2 μm)

2.5 粗糙度

通過在FLUENT軟件中設置氣膜兩側壁面粗糙度數值，模擬氣體軸承在不同表面粗糙度下的運動狀態。模擬計算時考慮粗糙度的影響，實際上是在湍流模型的壁面函數中包含了壁面粗糙度的影響。選取轉速為10 000、20 000、30 000 r/min，在表面粗糙度分別為0.1、0.2、0.4 μm情況下進行模擬仿真，得到其軸心運動軌跡以及不同轉速與表面粗糙度下軸心軌跡變化，如圖13(a)所示。可以看出：在定子與轉子表面粗糙度不超過0.4 μm時，轉子振幅在較小的范圍內上下波動，軸心軌跡均穩定在一定大小的橢圓內，如圖13(b)所示，對定子運動穩定性影響較小。

圖13 轉子幅值隨定子與轉子表面粗糙度變化及轉子軸心軌跡Fig 13 Variation of the amplitude of rotor with the surfaceroughness of the rotor and rotor axis orbit (a)amplitude under different speeds and surfaceroughness;(b)axis orbit (30 000r/min,roughness 0.4 μm)

3 結論

針對螺旋槽動靜壓氣體軸承建立了CFD-6DOF流固耦合仿真模型，針對加工及裝配誤差對轉子運動穩定性的影響進行了仿真分析，得到的主要結論如下：

(1)裝配誤差對軸承運動穩定性影響較大，當轉速達到30 000 r/min，定子軸線偏移誤差以及定子軸線傾斜誤差分別達到2 μm以及2°時，轉子振幅增加明顯，軸承運動狀態均為極限環運動，處于臨界穩定狀態。為保證氣體軸承運動穩定性，應確保氣體軸承的軸線裝配精度。

(2)在保證軸承對中良好的情況下加工誤差對軸承運動穩定性影響較小。當定子尺寸誤差小于1 μm時，轉子振幅增大的幅度較小，達到2 μm時，增幅略為明顯；當表面粗糙度值不超過0.4 μm時，轉子振幅在較小的范圍內上下波動，軸承依然保持穩定。