神經(jīng)網(wǎng)絡(luò)優(yōu)化算法與《最優(yōu)化方法》課程教學(xué)融合研究

孫杰寶 楊暢 吳勃英

摘?要：近年來，人工智能在學(xué)術(shù)界和工業(yè)界都取得了極大的成功，這正是由于深度神經(jīng)網(wǎng)絡(luò)在最近十年內(nèi)的飛速發(fā)展。神經(jīng)網(wǎng)絡(luò)模型的目標就是最優(yōu)化，對一個復(fù)雜的問題中作出最優(yōu)決策。幾乎所有的神經(jīng)網(wǎng)絡(luò)模型都可以建模為一個優(yōu)化問題。本文就求解神經(jīng)網(wǎng)絡(luò)模型過程中涉及的優(yōu)化算法進行總結(jié)，并對《最優(yōu)化方法》課程教學(xué)內(nèi)容進行了探索。通過將神經(jīng)網(wǎng)絡(luò)模型及其優(yōu)化算法與《最優(yōu)化方法》課程教學(xué)融合，使學(xué)生熟悉并掌握其原理和優(yōu)化求解方法，具備更強的核心競爭力。

關(guān)鍵詞：人工智能;最優(yōu)化方法;神經(jīng)網(wǎng)絡(luò)

中圖分類號：G420?文獻標識碼：C

Abstract：In recent years，artificial intelligence has achieved great success in academia and industry.This is due to the rapid development of deep neural network in recent ten years.The goal of neural network model is optimization，that is making optimal decision in a complex problem.Almost all neural network models can be modeled as an optimization problem.In this paper，we summary the optimization algorithms involved in the process of solving neural network models，and explore the teaching content of optimization method.Through the integration of neural network model and its optimization algorithm with the teaching of optimization method，students can master its principle and optimization method，and have stronger core competitiveness.

Keywords：Artificial Intelligence;Optimization method;Neural network

一、概述

隨著人工智能的不斷發(fā)展和在社會各個領(lǐng)域應(yīng)用的不斷深入，人們逐漸切實領(lǐng)略到其改變?nèi)祟惿罘绞降臐摿Α嶋H中，存在很多對人類來說較為容易，但卻難以通過數(shù)學(xué)公式表達的問題，如語音識別、人臉識別。人往往能夠通過經(jīng)驗輕松地處理這些問題。由于深度神經(jīng)網(wǎng)絡(luò)能夠從大量的樣本中提取內(nèi)在的語義特征、學(xué)習(xí)經(jīng)驗并做出決策，其在處理這類的任務(wù)方面有著出色的表現(xiàn)。神經(jīng)網(wǎng)絡(luò)模型是目前人工智能中表現(xiàn)最為優(yōu)秀的算法之一。

優(yōu)化算法需要大量的數(shù)值計算，通常情況下是指通過迭代過程更新解的估計值來解決數(shù)學(xué)問題的算法。最優(yōu)化方法[1]在這個訓(xùn)練學(xué)習(xí)的過程中起著重要的作用，是求解模型的關(guān)鍵。作為人工智能實現(xiàn)模塊的核心工具之一，學(xué)習(xí)并掌握一定的優(yōu)化算法的重要性也日趨顯著。教育的變革不應(yīng)當(dāng)僅僅局限于教學(xué)方法探索方面，更應(yīng)該緊跟國家發(fā)展的戰(zhàn)略與方向，與時俱進提出新的教學(xué)理念，緊跟科學(xué)發(fā)展更新教學(xué)內(nèi)容，從而精準地定位培養(yǎng)目標。社會發(fā)展是課程改革和教育發(fā)展的原動力。對當(dāng)代教育來說更應(yīng)該培養(yǎng)學(xué)生在掌握專業(yè)知識的同時，具備將所學(xué)知識應(yīng)用到我國發(fā)展中所面臨的實際問題的能力。因此，最優(yōu)化方法的課程內(nèi)容如何與當(dāng)前社會實際應(yīng)用相匹配、如何體現(xiàn)本課程特色、如何滿足當(dāng)前社會與行業(yè)的人才需求等問題一直是教學(xué)工作中需要關(guān)注和思考的問題。

二、課程教學(xué)改革的必要性

在21世紀，在物聯(lián)網(wǎng)技術(shù)高速發(fā)展的同時，如何培養(yǎng)同時具備理論分析和實踐應(yīng)用的創(chuàng)新性人才是極為重要的。這也是最優(yōu)化方法課程改革不可避免要面對的問題。

隨著互聯(lián)網(wǎng)與計算機硬件的不斷發(fā)展，近20年來，各行各業(yè)都積累了大量的數(shù)據(jù)。人類對數(shù)據(jù)的采集、存儲、傳輸及處理能力飛速提升。因此，亟須有效的數(shù)據(jù)分析算法來合理利用這些數(shù)據(jù)。機器學(xué)習(xí)[2]恰巧滿足了處理海量數(shù)據(jù)的迫切需求。實際上，科學(xué)研究的模式方法由傳統(tǒng)的“理論+實踐”到如今的“理論+實驗+計算”，以至近年來流行的“數(shù)據(jù)科學(xué)”，機器學(xué)習(xí)扮演著越來越重要的角色。數(shù)據(jù)科學(xué)的核心是通過對數(shù)據(jù)進行分析從而獲取有價值的信息，數(shù)據(jù)分析是以“計算”為依托的。現(xiàn)如今，在多媒體、圖形學(xué)以及網(wǎng)絡(luò)通信、軟件工程，甚至芯片設(shè)計、體系結(jié)構(gòu)等計算機學(xué)科的分支領(lǐng)域中，機器學(xué)習(xí)的身影無處不在。此外，機器學(xué)習(xí)已經(jīng)成為推動計算機視覺、自然語言處理等計算機應(yīng)用技術(shù)領(lǐng)域向前發(fā)展最重要的動力源泉。

人工智能的目標就是最優(yōu)化，在一個復(fù)雜的環(huán)境中做出最優(yōu)決策，幾乎所有的人工智能問題都可以建模為一個優(yōu)化問題。最優(yōu)化理論可以判定人工智能目標函數(shù)的最大值、最小值是否存在，并且可以尋找到滿足最優(yōu)目標的數(shù)值。機器學(xué)習(xí)算法在人工智能領(lǐng)域中扮演著至關(guān)重要的角色，是人工智能中的核心技術(shù)，將其引入最優(yōu)化課程中，在拓寬學(xué)生知識面的同時還能夠讓學(xué)生掌握最先進的科學(xué)技術(shù)，從而提高學(xué)生在就業(yè)中的競爭力。在本科生、研究生教學(xué)中，引導(dǎo)學(xué)生思考、探索最前沿的科學(xué)問題是一項重要的任務(wù)。數(shù)值優(yōu)化算法是機器學(xué)習(xí)求解的基本策略，所以將其相融合是一個很自然的想法。這恰恰為學(xué)生創(chuàng)新能力的培養(yǎng)提供了素材。鑒于此，將人工智能中的神經(jīng)網(wǎng)絡(luò)模型引入《最優(yōu)化方法》課程是非常有必要的。

如何將最優(yōu)化方法中被廣泛應(yīng)用的一些工具性算法與其嚴謹又抽象的數(shù)學(xué)理論相結(jié)合，是廣大數(shù)學(xué)教育工作者堅持不懈的目標。這種結(jié)合一方面可以使得學(xué)生接受嚴格數(shù)學(xué)理論的熏陶，培養(yǎng)嚴謹?shù)臄?shù)學(xué)思維，同時又能夠熟練掌握相應(yīng)的計算方法，為后續(xù)課程的學(xué)習(xí)與科學(xué)研究奠定基礎(chǔ)[4-6]。當(dāng)前的最優(yōu)化方法課程教學(xué)內(nèi)容主要包括傳統(tǒng)的凸優(yōu)化算法的基本概念、基本理論、基本方法和基本算法，其重點是理論基礎(chǔ)和基本技術(shù)，尚未包含人工智能的相關(guān)內(nèi)容。因此，有必要從求解神經(jīng)網(wǎng)絡(luò)模型的角度對最優(yōu)化方法課程教學(xué)內(nèi)容進行更新探索。

三、神經(jīng)網(wǎng)絡(luò)中的優(yōu)化教學(xué)內(nèi)容探索

神經(jīng)網(wǎng)絡(luò)模型是目前最具代表性的人工智能算法。人工智能的目標就是最優(yōu)化：在復(fù)雜環(huán)境與多體交互中做出最優(yōu)決策。幾乎所有的人工智能問題最后都會歸結(jié)為一個優(yōu)化問題的求解，因而最優(yōu)化理論與方法是人工智能必備的基礎(chǔ)知識。深度學(xué)習(xí)[3]優(yōu)化算法與純優(yōu)化算法最大的區(qū)別在于目標不同。純優(yōu)化是找到優(yōu)化問題的最優(yōu)解，比如能量最小點，但是深度學(xué)習(xí)其實只是借用了純優(yōu)化的手段，最終的目的是讓模型的泛化誤差最小。深度學(xué)習(xí)優(yōu)化算法有很多，例如：SGD（隨機梯度下降法）、動量方法、Adagrad自適應(yīng)學(xué)習(xí)率調(diào)整方法、Adam、Nadam等。下面首先介紹神經(jīng)網(wǎng)絡(luò)模型，再介紹求解神經(jīng)網(wǎng)絡(luò)模型過程中經(jīng)常使用的優(yōu)化算法：梯度下降法。

（一）神經(jīng)網(wǎng)絡(luò)[2]

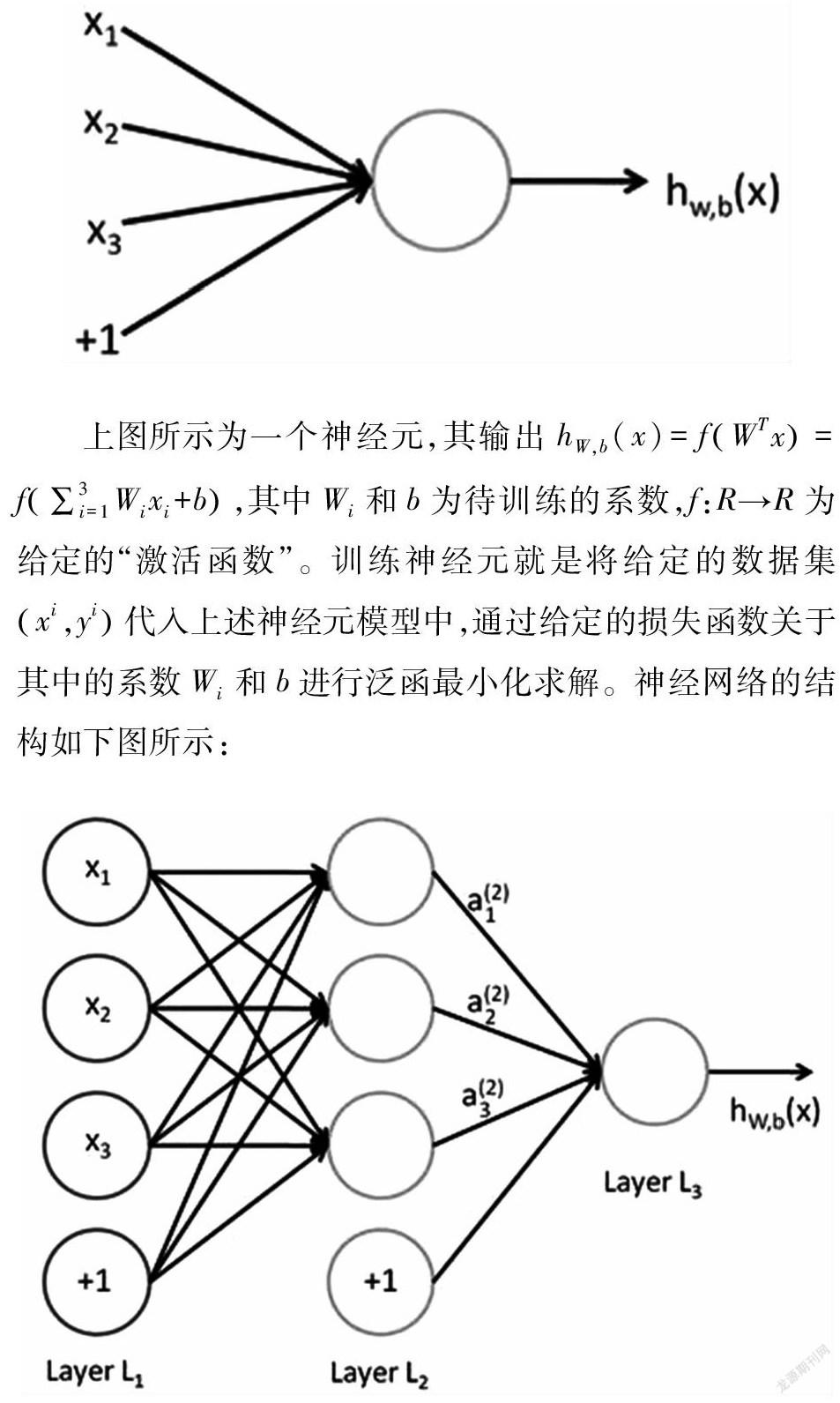
神經(jīng)網(wǎng)絡(luò)模型：假設(shè)有訓(xùn)練樣本集xi，yi：

這里的藍色圓圈表示輸入，“+1”代表偏置節(jié)點，即截距。上圖中最左邊一列為輸入層，最右邊一列為輸出層（本文上例中輸出層為單一節(jié)點）。中間的部分稱為隱藏層，這是由于中間的隱藏層是通過輸入層與損失函數(shù)數(shù)據(jù)計算得來的，其具體的值并不能直接觀察得到。

（二）反向傳播與梯度下降法[2]

這部分，本文介紹如何通過反向傳播與梯度下降法求解神經(jīng)網(wǎng)絡(luò)的參數(shù)（W，b）。首先，設(shè)樣本集為：

其為m個樣例構(gòu)成的集合，x為神經(jīng)網(wǎng)絡(luò)的輸入，y為期望的輸出值。對于單個（x，y），本文研究的損失函數(shù)為：

對于包含m個樣例的數(shù)據(jù)集，整體的損失函數(shù)為：

為了防止過擬合，增加上式中的正則化項（第二項）來降低權(quán)重的值。

針對上述損失函數(shù)，梯度下降法為按照下列公式更新參數(shù)W和b：

通過梯度下降法迭代過程，減小代價函數(shù)J（W，b），得到最優(yōu)的參數(shù)W和b。

結(jié)論

“人工智能”不僅是一項科學(xué)技術(shù)，更是一種可以認識當(dāng)下萬事萬物的思維方式。本文基于應(yīng)用這樣的認知邏輯到實際問題中，從教育的角度出發(fā)，將人工智能中的神經(jīng)網(wǎng)絡(luò)算法求解融入最優(yōu)化方法課程內(nèi)容當(dāng)中。希望把握國家發(fā)展戰(zhàn)略與教育變革發(fā)展方向，探索實現(xiàn)教育變革的路徑，使得學(xué)校教育緊跟時代發(fā)展的步調(diào)與方向。此外，當(dāng)前機器學(xué)習(xí)取得的一系列優(yōu)秀成果使得其被廣泛應(yīng)用到各行各業(yè)，機器已經(jīng)開始取代一些器械重復(fù)性的工作。在此趨勢之下，學(xué)生對于神經(jīng)網(wǎng)絡(luò)原理與最優(yōu)化方法的學(xué)習(xí)與掌握將極大地提高其在就業(yè)市場的核心競爭力。

《最優(yōu)化方法》改革建議：在向同學(xué)們講解一般的優(yōu)化方法的同時，也介紹一些神經(jīng)網(wǎng)絡(luò)優(yōu)化中出現(xiàn)的問題及一般的解決辦法。同時將神經(jīng)網(wǎng)絡(luò)優(yōu)化中的實際問題提煉出來交給學(xué)生去做，讓學(xué)生通過查閱文獻、交流討論、編程實現(xiàn)來解決實際問題并對其中的問題做相應(yīng)的理論分析。這不僅能夠使得教學(xué)內(nèi)容與時俱進，提高學(xué)生對最優(yōu)化方法的理解，同時也能鍛煉學(xué)生查閱資料、合作與動手能力。

參考文獻：

[1]袁亞湘，孫文瑜.最優(yōu)化理論與方法[M].科學(xué)出版社，1997.

[2]周志華.機器學(xué)習(xí)[M].清華大學(xué)出版社，2016.

[3]伊恩·古德費洛，約書亞·本吉奧，亞倫·庫維爾.深度學(xué)習(xí)[M].人民郵電出版社，2017.

[4]王永建，楊建華，郭廣濤，王治東.面向最優(yōu)化問題的人工智能搜索算法研究[J].通信技術(shù)，2016，49（11）：1459-1465.

[5]孫杰寶，吳勃英，張達治.《最優(yōu)化方法》課程教學(xué)法研究與實踐[J].大學(xué)數(shù)學(xué)，2016，33（3）：120-124.

[6]李明奇，杜鴻飛.最優(yōu)化建模實驗中的可視化設(shè)計[J].大學(xué)數(shù)學(xué)，2014，30（4）：19-23.

基金項目：黑龍江省高等教育教學(xué)改革研究項目“人工智能驅(qū)動下的《最優(yōu)化方法》課程教學(xué)改革”（SJGY2019 0224）;中國高等教育學(xué)會理科教育專業(yè)委員會高等理科教育研究課題“新時代下數(shù)學(xué)學(xué)科拔尖人才培養(yǎng)模式研究與實踐”（20ZSLKJYZD12）;哈爾濱工業(yè)大學(xué)研究生教育教學(xué)改革研究重點項目“數(shù)學(xué)學(xué)科杰出人才培養(yǎng)模式探索與實踐”

作者簡介：孫杰寶（1977—?），男，黑龍江雙鴨山人，博士，哈爾濱工業(yè)大學(xué)教授，從事計算數(shù)學(xué)研究;楊暢（1983—?），男，湖北武漢人，博士，哈爾濱工業(yè)大學(xué)副教授，從事計算數(shù)學(xué)研究;吳勃英（1961—?），女，黑龍江哈爾濱人，博士，哈爾濱工業(yè)大學(xué)教授，從事計算數(shù)學(xué)研究。