初高中數學函數教學銜接性的實踐研究

◎侯 嬌

(吉林師范大學,吉林 長春 130000)

前 言

數學是教學階段中不可缺少的工具學科，是學生學習物理、化學等科目的工具，更是研究數量關系與空間形式的學科，數學學習有利于培養學生的智力與能力.函數是初高中數學教學的關鍵，其思想與方法滲透到了數列、幾何、不等式、方式、代數、概率等各個方面，所以，函數的學習對學生的能力有較高的要求.為了提高學生的函數掌握程度，教師應該將初高中數學函數教學有機地銜接起來.

1 初高中數學函數教學的聯系與區別

隨著新課程改革的深入實施，數學函數教學逐漸向更加科學與細致的方向發展.目前，我國中學數學課程主要分為初中數學課程與高中數學課程兩部分，而新課標也對函數教學進行了詳細解釋與說明，為不同教育階段的教學提供了依據.初高中數學函數教學具有一定的聯系，但也有一定的區別.

1.1 初高中數學函數教學的聯系

從新課標對初高中函數內容的要求來看，初高中的函數知識雖然緊密相連，層層遞進，但是初高中的函數知識存在著天壤之別，函數知識的區別與聯系潛移默化地影響著學生的數學學習.在日常教學中，教師要根據學生的知識基礎，通過延伸、類比等方法將其納入知識框架中，從而增進學生對新知識的理解.初中函數教學是開展高中函數教學的前提和基礎，在初中學習函數的概念(變量說)以及各類函數的定義及性質等內容可以為學生更輕松地學習高中函數知識提供幫助[1].初中函數的學習是通過簡單的定義讓學生更好地理解函數的抽象性，這樣才能夠在進入高中之后更好地理解函數變量之間的關系.初高中數學函數知識聯系最緊密的是二次函數，在初中學習過程中，二次函數知識放在了初三，同時二次函數知識得到了很多教師和學生的重視，初中二次函數的學習也為高中二次函數的進一步學習奠定了基礎.另外，初中方程知識的學習對于高中根與系數的關系的學習做好了鋪墊；初中冪的計算的學習為高中指數函數以及對數函數內容的學習奠定了基礎.因此，初高中函數教學之間有較大的聯系.

1.2 初高中數學函數教學的區別

雖然初高中函數教學有很多的聯系，但是其內容、方法等各個方面都有不同，而這些不同之處與學生的認知結構、心理特征以及智力發育等因素也有直接關系.首先，初高中函數概念不同.初中教材中定義函數的方法是變量方法，而高中教材中函數的定義是以集合論為基礎的，因此高中教材中函數的定義是：給定一個非空的數集A，對A施加對應法則f，記作f(A),得到另一個數集B，也就是B=f(A).那么這個關系就叫作函數關系式，簡稱函數[2].因此，高中更加強調函數是一種對應關系.其次，初高中對函數的教學要求不同.初中只要求學生對函數有最基本的了解，只需了解一次函數、二次函數以及反比例函數的形式與應用，而在高中則對學生的要求更高，要求學生能夠熟練應用冪函數、指數函數、三角函數、對數函數等函數，要求學生透徹理解這些函數的性質，并且對函數的習題能夠靈活解決[3].此外，初高中教材關于函數知識的編寫不同，難度也不同，具有較大的差別.更重要的是，初中函數知識相對簡單，內容易理解，而高中函數知識內容相對復雜，需要學生有隨機應變的能力.

2 初高中數學函數教學銜接性的實踐策略

要想將初高中數學函數教學銜接起來，就需要將教學內容、教法以及學法銜接起來.

2.1 明確教材銜接點，實現教學內容的銜接

人教A版教材是初高中的常用教材，但是初中和高中的教材有較大的差別，編寫特點與思維都存在區別，因此，教師需要明確教材的銜接點，實現教材內容的銜接，科學利用教材當中已有的銜接內容，例如，在初中學習冪的知識時，教師可以為學生設置一些課外拓展題，讓學生提前認識冪函數以及對數函數，為高中冪函數、對數函數的學習做基礎.在新課程改革后，初高中數學教材出現了一定的變化，且都趨向于理論聯系實際，希望能夠以此調動學生學習的積極性，培養學生的數學思維能力及創造力，讓數學教育“活”起來.但是，初中數學教材當中的內容較為簡單，語言表達也比較簡單，而高中教材內容則較難.部分初中教師對高中教材并不熟悉，只是根據初中教學要求開展教學工作，沒有科學把握高中函數學習所需要銜接的知識[4].而高中教師對初中教材也不是很了解，認為學生能夠直接理解高中教材，這就導致了函數教學嚴重脫節.

在這種情況下，高中教師有必要研讀初中教學課程標準，并參考中考題，找到初高中函數教學的銜接點，將教學內容銜接起來.例如，已知函數y=f(x)，當x取何值時，y=0？這就相當于求f(x)=0的解，而x的值就是函數圖象與x軸交點的橫坐標.另外，也可以用一元不等式表示y與0之間的大小關系.所以，初中教師在講解這部分內容時，可以將函數、方程以及不等式等內容銜接起來，為后續學習“方程的根與函數的零點”這一部分內容奠定基礎.(如下表所示)[5].

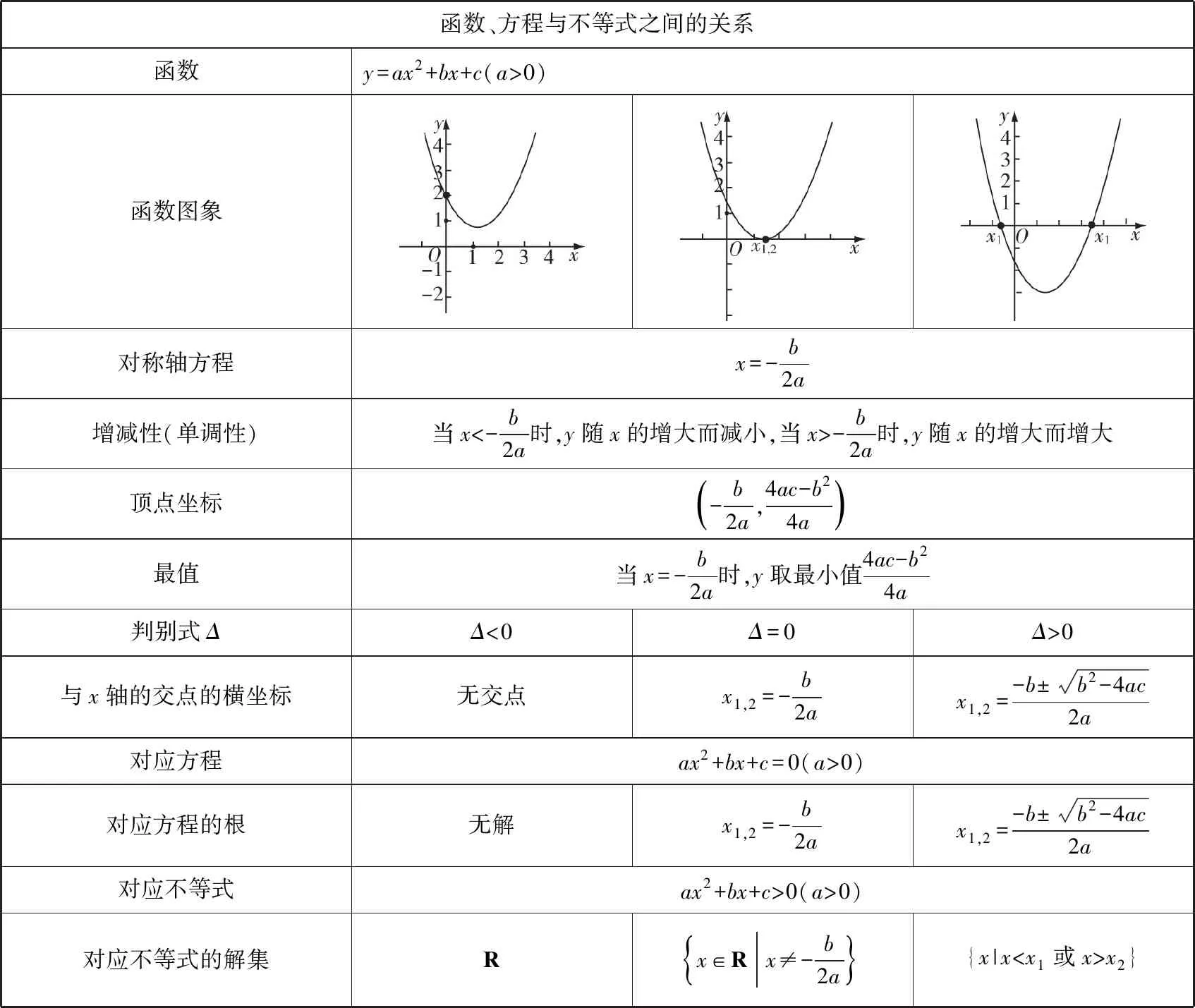
函數、方程與不等式之間的關系

另外，教師還應該根據教學實際補充教學內容，從而實現教材銜接.為了讓學生更好地接受新知識，教師應該從學生熟悉的舊知識入手，降低學生的學習難度，進而達到溫故而知新的目的.在教學過程中，教師應該根據精選以及交叉等原則，掌握初高中函數教學內容的交匯點，并根據教學內容，選取一些經典題型，從而解決教學內容的銜接問題.例如，在初中函數教學過程中，教師可以多為學生講解函數的起源、發展史，并且可以適當滲透集合思想，使學生進入高中之后能更好地接受集合論下的函數概念[6].同時，教師也可以適當講解一次以及二次函數、方程、不等式之間的關系，并且在講解的過程中要做到圖文并茂，例如，利用幾何畫板向學生展示圖形在變化過程中的關系.在講解不等式時，教師可以將不等式與函數圖象聯系起來.

2.2 加強教法研究，實現教法銜接

初高中教學方法的不同導致初高中函數教學存在嚴重的脫節現象，所以，教師應該加大對教法的研究力度，實現教學方法的銜接.第一，教師應當了解學生的數學基礎、知識儲備等各方面情況，積極開展因材施教.從實際情況來看，學生學習新知識是以舊知識為基礎的，即從舊知識出發，尋覓新舊知識之間的聯系，利用舊知識引出新知識，進而逐漸滲透新知識，從而降低學習難度.因此，在備課過程中，教師應當深入分析學生的實際情況，以提升教學效率.例如，在高中剛開學時，教師可以對學生進行測試，從而了解學生的情況.為了增強測試的針對性，教師應該對學生進行專門的函數測試，進而全面掌握學生對函數知識的了解情況[7].之后，再根據學生課堂生成表現來制訂適合本班級學生的教學計劃，進而使教學更高效.第二，教師應當重視數學語言教學，提高學生的理解能力.數學語言較為獨特，不僅包括文字，還包括符號、圖象以及圖形，并且數學語言十分精煉準確，但是理解難度較大.如果不理解數學語言，就不能理解數學思想，所以，教師應該加強數學語言教學，讓學生了解各種符號、圖形以及圖象.第三，教師應該優化教育管理環節，進而實現初高中函數教學的有效銜接.教師在進行銜接內容的滲透教學時要做充分的準備，不然會導致學生處于被動狀態當中，要體現滲透這一特點，讓學生在不知不覺、潛移默化當中掌握銜接內容[8].第四，教師應該做好培優輔差工作，尤其是對初中數學內容掌握不太好的學生，教師可以抽空為學生補齊初中數學內容，使其能夠更好地接受高中數學內容.在作業布置方面，教師應該分層處理，對于優生，要布置創新型的習題，培養優生的數學思維，對于中等生，要布置基礎題以及經過思考能夠解答的題目，提高中等生的學習積極性，使中等生能夠向優生轉變，對于待優生，要布置一些基礎題目，使其學生能夠通過完成作業來鞏固當天學習的內容，并增加自信心.只有這樣，才能實現培優輔差的目的，使每個學生都有題可做，從而增強學生的學習積極性，調動學生的學習能動性.另外，教師在教學過程中也要重視數學思想的滲透，比如，數形結合思想、分類討論思想等，在數學思想的支撐下，學生對于數學知識的理解將會更加深入.

2.3 注重學法指導，實現學法銜接

除了教法，學法也十分重要，初中數學內容相對簡單，所以部分學生沒有形成系統科學的學習方法，而高中數學內容相對復雜，因此，學生在剛入學的學習中會感到吃力.基于此，首先，教師在課堂教學中要有意識地培養學生的自主學習能力.在高中階段甚至以后的學習過程中，自學將伴隨學生的一生，學生的自學能力強，那么學生的數學思維提升得就很快.另外，初中生比較善于表現自我，但高中生則相對沉默，有較強的自我意識.所以，高中數學教師在備課時需要綜合考慮學生的情況，為學生創設一個輕松自由的環境，鼓勵學生表達自己的想法，讓學生積極參與教學過程，只有學生善于表達，積極參與教學活動，學生的學習成績才能有所提升.教師也可以大膽地將課堂還給學生，鼓勵學生上臺展示.其次，學生對于動畫的感知能力強，教師需要多利用多媒體進行教學.數形結合是數學中的重要思想，也是解決函數問題的關鍵，所以，教師需要通過多媒體教學等方式增強學生這方面的意識.例如，教師可以利用幾何畫板、Flash等軟件處理函數圖象，讓學生從圖象的角度出發，靈活轉化符號、文字以及圖象語言，進而解決抽象的、不易理解的函數問題[9].另外，學生在學習的過程中不能偷懶，對于函數與方程部分的內容，學生要通過教師滲透的數學思想發散思維，積極地去寫去畫，運用數學思想理解知識，只有知其原理才能懂其應用.對于數學知識，學生最容易忽視的就是對于知識的記憶，因此，高中教師要為學生講明原理，幫助學生更好地記憶數學知識.比如，在講方程的根與函數的零點的關系時，教師要剖析什么是方程的根，什么是函數的零點，找到兩者之間的關系，對最基本的知識進行拓展，進而靈活應用.

結 語

在內在因素與外在因素的共同影響下，初高中數學教學脫節現象十分嚴重，而將初高中數學函數教學銜接起來有重要意義，所以，教師應明確初高中數學函數教學之間的聯系與區別.同時，教師應明確教材銜接點，實現教學內容的銜接；優化教學方法，實現教學方法的銜接；指導學生有效學習，實現學法的銜接，從而增進學生對函數知識的了解，提高教學質量.