探究奇數與素數之間的聯系

◎王國昌

(英林學校，黑龍江 雞西市 158180)

1 引 言

數學的加、減、乘、除、乘方、開方等的基本運算都是以整數的運算為基礎，而整數的運算又是以素數的運算為基礎，因此，素數的性質就顯得格外重要.素數受其定義的約束，因此具備的性質少之又少，正因如此在素數領域的研究每取得一點成績都顯得彌足珍貴.經過十幾年不懈的探索，我對素數有了更進一步的了解，同時獲得了一些自己的心得體會，現在我把它提出來，與大家共同探討.

2 命題及概述

對于哥德巴赫猜想內容：“任何不小于7的奇數都可以用三個素數之和表示.”[1]，許許多多的科研工作者經過多年的計算都認為是正確的，但至今仍然無法給出一個完整的證明，其證明難度之大可想而知.因此筆者認為人們除了需要集中很大的力量進行證明哥德巴赫猜想之外，還應該有一部分人繞開這個難點，去研究一個奇數用三個素數之和表示時有多少種不同的情況，以及其他相關的性質.牛頓發現微積分的時候，并沒有證明微積分是正確的，當時也不為許多人所接受，但牛頓并沒有執著于證明微積分的正確性，而是用微積分解決了生活和生產中的實際問題，為科學做出了巨大的貢獻.牛頓的這種做法給了我們一個啟示，就是當前進的途中如果障礙太大，我們不妨設法繞過去，同樣可以到達目的地.因此，筆者試圖從另一個途徑來說明哥德巴赫猜想是正確的，同時更進一步闡明，奇數m(m≥7)不但一定能用三個素數之和表示，而且用三個素數之和表示的具體個數也是有規律的，有一定的范圍，是通過計算可以預知的.經過認真地思考，我總結出了下面這個命題.

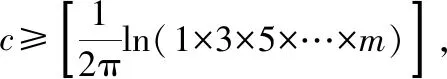
從公式中可以看出，一個奇數m(m≥7)用三個素數之和表示的個數僅與這個奇數的大小有關.從命題中還可以看出，一個奇數m(m≥7)用三個素數之和表示的個數的最小值是可以預測的.命題把最小的素數2、圓周率π以及不大于m的奇數的自然對數有機地結合起來，給人一種簡單、科學、自然、和諧的美感，增加了命題的使用價值.

下面列舉了7～300的部分有代表性的奇數用三個素數之和表示的情況.

7=2+2+3,

9=2+2+5=3+3+3,

11=2+2+7=3+3+5,

13=3+3+7=3+5+5,

15=2+2+11=3+5+7=5+5+5,

17=2+2+13=3+3+11=3+7+7=5+5+7,

19=3+3+13=3+5+11=5+7+7,

21=2+2+17=3+5+13=3+7+11=5+5+11=7+7+7,

23=2+2+19=3+3+17=3+7+13=5+5+13=5+7+11,

25=3+3+19=3+5+17=3+11+11=5+7+13=7+7+11,

27=2+2+23=3+5+19=3+7+17=3+11+13=5+5+17

=5+11+11=7+7+13,

29=3+3+23=3+7+19=3+13+13=5+5+19=5+7+17

=5+11+13=7+11+11,

31=3+5+23=3+11+17=5+7+19=5+13+13=7+7+17

=7+11+13,

33=2+2+29=3+7+23=3+11+19=3+13+17=5+5+23

=5+11+17=7+7+19=7+13+13=11+11+11,

35=2+2+31=3+3+29=3+13+19=5+7+23=5+11+19

=5+13+17

=7+11+17=11+11+13,

37=3+3+31=3+5+29=3+11+23=3+17+17=5+13+19

=7+7+23=7+11+19=7+13+17=11+13+13,

… …

75=2+2+71=3+5+67=3+11+61=3+13+59

=3+19+53=3+29+43=3+31+41=5+11+59

=5+17+53=5+23+47=5+29+41=7+7+61=7+31+37=11+11+53=11+17+47=11+23+41=13+19+43=13+31+31=17+17+41=17+29+29=19+19+37=23+23+29,

77=2+2+73=3+3+71=3+7+67=3+13+61=3+31+43

=3+37+37=5+5+67=5+11+61=5+13+59=5+19+53

=5+29+43=5+31+41=7+11+59=7+17+53

=7+23+47

=7+29+41=11+13+53=11+19+47=11+23+43

=11+29+37=13+17+47=13+23+41=17+17+43

=17+19+41=17+23+37

=17+29+31=19+29+29=23+23+31,

79=3+3+73=3+5+71=3+17+59=3+23+53=3+29+47

=5+7+67=5+13+61=5+31+43=5+37+37=7+11+61

=7+13+59=7+19+53=7+29+43=7+31+41

=11+31+37=13+13+53=13+19+47=13+23+43

=13+29+37=17+19+43=17+31+31=19+19+41

=19+23+37=19+29+31,

81=3+5+73=3+7+71=3+11+67=3+17+61=3+19+59

=3+31+47=3+37+41=5+5+71=5+17+59=5+23+53

=5+29+47=7+7+67=7+13+61=7+31+43=7+37+37

=11+11+59=11+17+53=11+23+47=11+29+41

=13+31+37=17+17+47=17+23+41=19+19+43

=19+31+31=23+29+29,

83=2+2+79=3+7+73=3+13+67=3+19+61=3+37+43

=5+5+73=5+7+71=5+11+67=5+17+61=5+19+59

=5+31+47=5+37+41=7+17+59=7+23+53

=7+29+47=11+11+61=11+13+59=11+19+53

=11+29+43=11+31+41=13+17+53=13+23+47

=13+29+41=17+19+47=17+23+43=17+29+37

=19+23+41=23+23+37=23+29+31

85=3+3+79=3+11+71=3+23+59=3+29+53=3+41+41

=5+7+73=5+13+67=5+19+61=5+37+43=7+7+71

=7+11+67=7+17+61=7+19+59=7+31+47

=7+37+41=11+13+61=11+31+43=11+37+37

=13+13+59=13+19+53=13+29+43=13+31+41

=17+31+37=19+19+47=19+23+43=19+29+37

=23+31+31,

87=2+2+83=3+5+79=3+11+73=3+13+71

=3+17+67=3+23+61=3+31+53=3+37+47

=3+41+43=5+11+71=5+23+59=5+29+53

=5+41+41=7+7+73=7+13+67=7+19+61

=7+37+43=11+17+59=11+23+53=11+29+47

=13+13+61=13+31+43=13+37+37=17+17+53

=17+23+47=17+29+41=19+31+37=23+23+41

=29+29+29

89=3+3+83=3+7+79=3+13+73=3+19+67

=3+43+43=5+5+79=5+11+73=5+13+71

=5+17+67=5+23+61=5+31+53=5+37+47

=5+41+43=7+11+71=7+23+59=7+29+53

=7+41+41=11+11+67=11+17+61=11+19+59

=11+31+47=11+37+41=13+17+59=13+23+53

=13+29+47=17+19+53=17+29+43=17+31+41

=19+23+47=19+29+41=23+23+43=23+29+37

=29+29+31,

91=3+5+83=3+17+71=3+29+59=3+41+47

=5+7+79=5+13+73=5+19+67=5+43+43

=7+11+73=7+13+71=7+17+67=7+23+61

=7+31+53=7+37+47=7+41+43=11+13+67

=11+19+61=11+37+43=13+17+61=13+19+59

=13+31+47=13+37+41=17+31+43=17+37+37

=19+19+53=19+29+43=19+31+41=23+31+37

=29+31+31

… …

195=2+2+191=3+11+181=3+13+179=3+19+173

=3+29+163=3+41+151=3+43+149=3+53+139

=3+61+131=3+79+113=3+83+109=3+89+103

=5+11+179=5+17+173=5+23+167=5+41+149

=5+53+137=5+59+131=5+83+107=5+89+101

=7+7+181=7+31+157=7+37+151=7+61+127

=7+79+109=11+11+173=11+17+167

=11+47+137=11+53+131=11+71+113

=11+83+101=13+19+163=13+31+151

=13+43+139=13+73+109=13+79+103

=17+29+149=17+41+137=17+47+131

=17+71+107=17+89+89=19+19+157

=19+37+139=19+67+109=19+73+103

=19+79+97=23+23+149=23+41+131

=23+59+113=23+71+101=23+83+89

=29+29+137=29+53+113=29+59+107

=29+83+83=31+37+127=31+61+103

=31+67+97=37+61+97=37+79+79

=41+41+113=41+47+107=41+53+101

=41+71+83=43+43+109=43+73+79

=47+47+101=47+59+89=53+53+89

=53+59+83=53+71+71=61+61+73

=61+67+67,

255=2+2+251=3+11+241=3+13+239=3+19+233

=3+23+229=3+29+223=3+41+211=3+53+199

=3+59+193=3+61+191=3+71+181=3+73+179

=3+79+173=3+89+163=3+101+151=3+103+149

=3+113+139=5+11+239=5+17+233=5+23+227

=5+53+197=5+59+191=5+71+179=5+83+167

=5+101+149=5+113+137=7+7+241=7+19+229

=7+37+211=7+67+181=7+97+151=7+109+139

=11+11+233=11+17+227=11+47+197

=11+53+191=11+71+173=11+107+137

=11+113+131=13+13+229=13+19+223

=13+31+211=13+43+199=13+61+181

=13+79+163=13+103+139=17+41+197

=17+47+191=17+59+179=17+71+167

=17+89+149=17+101+137=17+107+131

=19+37+199=19+43+193=19+73+163

=19+79+157=19+97+139=19+109+127

=23+41+191=23+53+179=23+59+173

=23+83+149=23+101+131=29+29+197

=29+47+179=29+53+173=29+59+167

=29+89+137=29+113+113=31+31+193

=31+43+181=31+61+163=31+67+157

=31+73+151=31+97+127=37+37+181

=37+61+157=37+67+151=37+79+139

=37+109+109=41+41+173=41+47+167

=41+83+131=41+101+113=41+107+107

=43+61+151=43+73+139=43+103+109

=47+59+149=47+71+137=47+101+107

=53+53+149=53+71+131=53+89+113

=53+101+101=59+59+137=59+83+113

=59+89+107=61+67+127=61+97+97

=67+79+109=71+71+113=71+83+101

=73+73+109=73+79+103=79+79+97,

… …

由于受篇幅的限制，不可能把太多的奇數用三個素數之和表示的可能情況都列舉出來，因此，我列出了部分有代表性的奇數m，這些奇數用三個素數表示的個數c，與相鄰的奇數用三個素數表示的個數c相比較，要小一些，只要這些奇數符合命題，那么與它相鄰的奇數也符合命題.進而，可以判斷出所有的不小于7的奇數對于命題都成立，因此，說明命題是正確的.

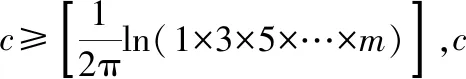
通過上面的計算我們可以發現，隨著奇數的增大，用三個素數之和表示的個數不斷變化，有時增大，有時減小，但整體上是呈現增大的趨勢，而且增大的速度較快.所以想用一個式子來表示奇數m用三個素數之和表示的具體個數是不可能的,但如果我們不需要知道用三個素數之和表示的具體個數，而只需要知道大約的個數，或者只需要知道最少有多少個，那么這個命題恰好解決了這個難題.

在通常的情況下，我們要想知道一個奇數m用三個素數之和表示大約有多少種不同的情況，需要先計算出所有不大于m的素數，再利用排列組合的方式寫出三個素數相加的所有的式子，僅僅這些式子就會占有很大的篇幅，然后計算出這些式子的和分別是多少，最后篩選出和等于m的符合要求的式子.隨著奇數m的逐漸增大，不大于m的素數的個數也會逐漸增加.雖然素數的個數增加較慢，但由這些素數中任意三個素數之和表示的個數卻會快速增大.如果將這些式子全部列出，不僅會占據非常大的篇幅,它的計算量的也會非常大，而且極易出現錯誤.其計算量之大和煩瑣的程度超出了我們的想象.但若要借助命題，就變得非常簡單了，手邊僅僅有一個計算器就可以了，這也是這個命題的實用價值之一.

另外，這個命題如果可以被證明是正確的，那么不但可以間接說明哥德巴赫猜想是正確的，而且通過公式可以看出，隨著奇數的增大，用三個素數之和表示的個數會逐漸增多，而且增多的個數呈現一定的規律.

總之，命題只要成立，即使我們現在還無法確定它的真正的使用價值，但隨著研究的深入，它的作用會越來越大.因此，這一命題是值得我們深入思考和研究的.