基于“PBL”學·教·評 “三位”一體深度行
——基于PBL的小學數學單元復習課教學實踐與探究

◎張海燕

(福建省廈門市集美區樂海小學，福建 廈門 361021)

“PBL”是 Problem-Based-Learning 的縮寫，即基于問題的學習.PBL教學模式可以有效地培養學生的問題解決能力、自主學習能力、實踐創新能力和終生學習能力.筆者提出的“基于PBL的小學數學單元復習課教學研究”是以問題學習為核心、以師、生的互動對話為形式、以建構體系為目標的，旨在改變傳統復習課教學理念與模式，以問題為導向，更大程度地驅動學生自主學習、深度探究，促進教師更新理念、建構教學，建立積極有效的評價機制，促進教學相長、整體提升、課程發展.

一、問題導學，引導學生深度學習

審視小學數學單元復習課教學現狀，發現仍然存在亟待解決的問題：學生主體缺失，再現受阻；教師引導不利，缺乏建構；練習缺乏開放性，學生難以拓展提升……基于PBL的小學數學單元復習課教學，筆者認為教師應當做好復習課教學的總設計師，根據單元核心內容與目標，創設真實有效、精巧恰當的問題情境，引導學生在課前自主復習，先學后教；在課中深入復習，整體建構；在課后拓展應用，提升素養.下面以“長方體和正方體的整理與復習”為例進行具體闡述.

1.課前自主整理，落實先學后教

單元復習課雖內容繁多，但都是已學知識，學生若在課前進行有效整理與復習，則不僅能彌補課堂教學時間的不足，提高復習時效，還能培養自主學習能力.因此，教師的扶放有度很重要：“扶”予方法：復習課前專門給學生介紹表格、思維導圖、錯題集圖等常見圖表的特點及整理知識的方法，并引導學生通過各種途徑，如查閱數學書、作業本、錯題集，上網查找資料或請教家長，來回憶并搜集相關的復習內容，還可引導學生編習題、寫反思、整理易錯題等，只要是有效的學習經歷就是一種良好的學習方法.“放”得精彩：“細心指導”后“大膽放手”，讓學生自主回顧與整理.學生可以選擇自主整理，大膽創新，展現個性，也可以小組合作進行回顧整理，取長補短，分享智慧[2].下面是學生在“長方體與正方體的整理與復習”的課前整理單：

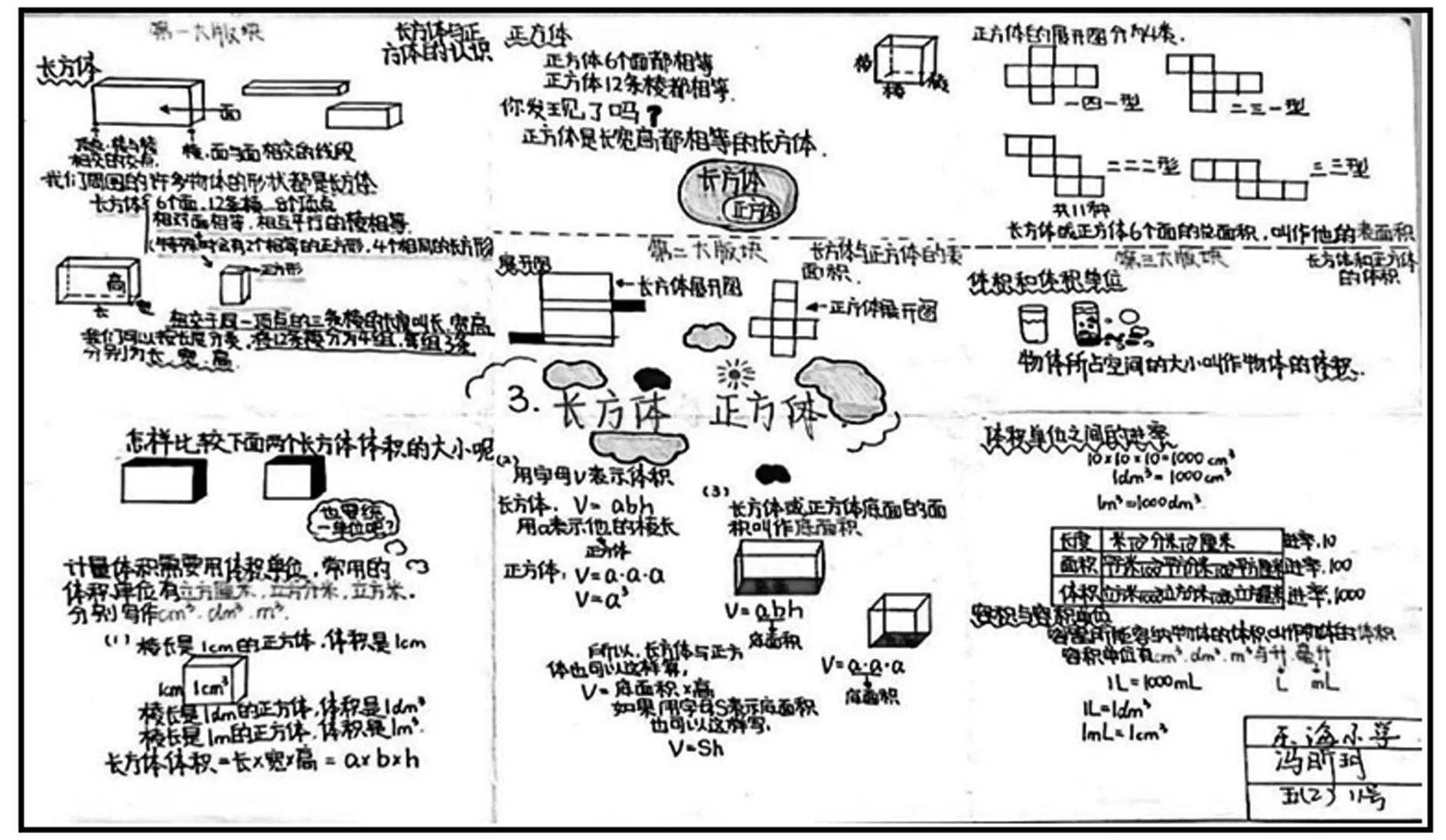
模塊整理圖：能有序歸納單元基礎知識，內容全面、條理清晰、表征多元，適合全體學生.

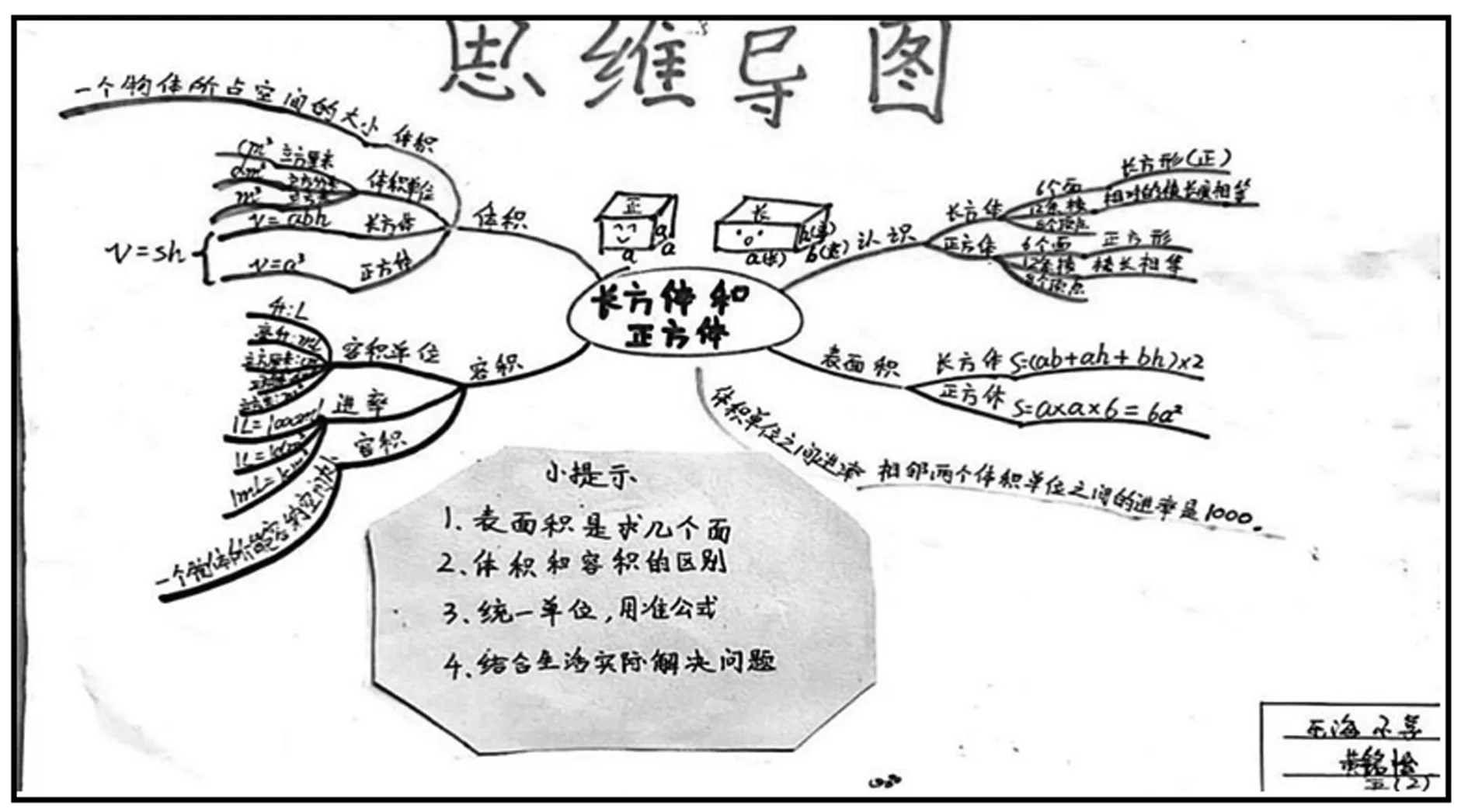
思維導圖：能溝通知識點、整理重難點、建構知識體系，體現學生嚴謹思維、獨特構想，展現學生個性特長.

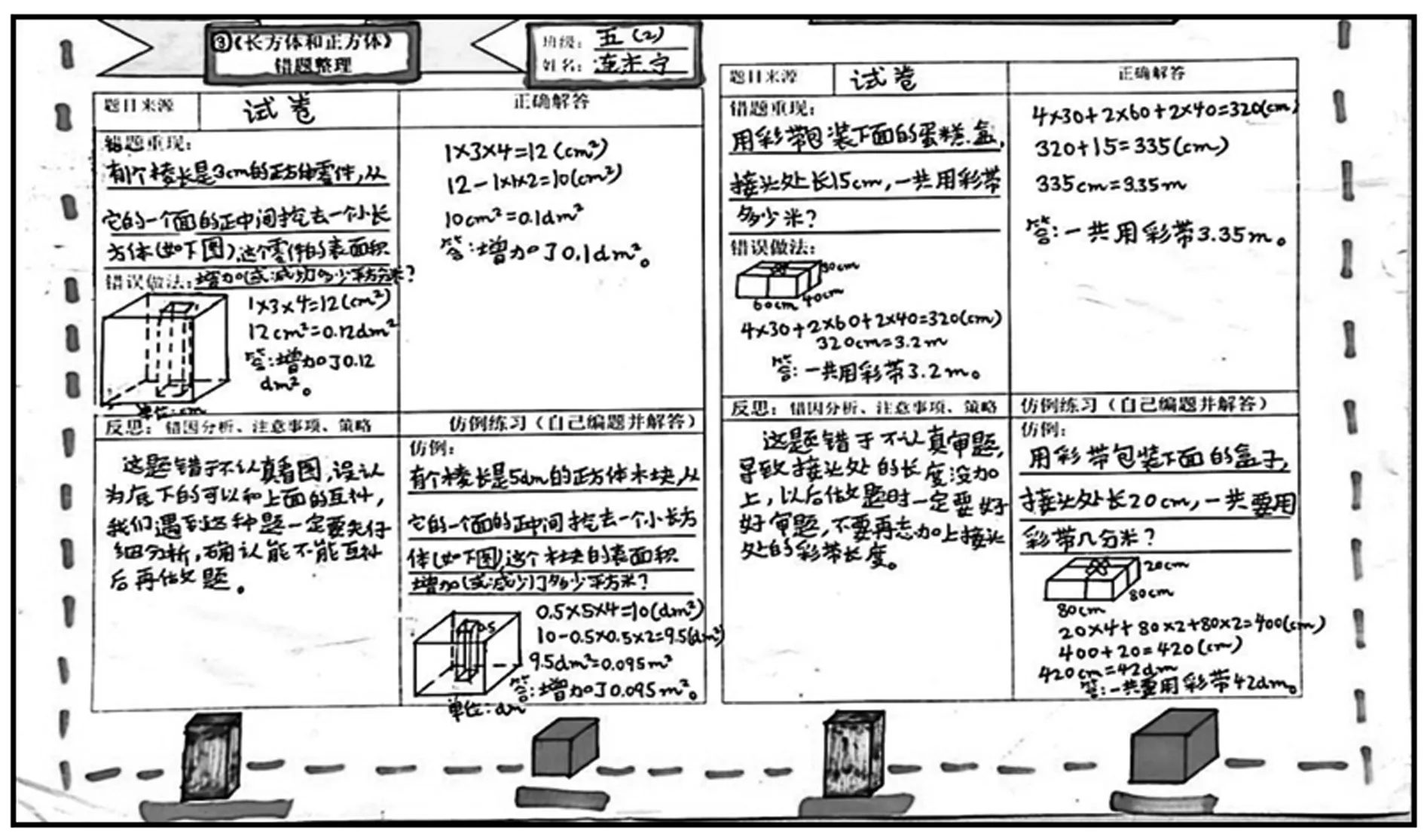
錯題集圖：能對所學知識進行查缺補漏、攻堅克難，使復習更有針對性，適合學優生.

教師引導學生帶著問題，對單元知識的內容進行自主整理、自我消化，學生根據實際情況，選擇教師設計好的表格或自己喜歡的圖文或制作錯題集等方式，做好單元知識的結構圖或思維導圖.這樣的“先學后教”喚醒了學生對單元知識的回憶與再現，為單元知識的進一步表征和復習奠定了基礎，使學生的學習變得更主動、生動且靈動.

2.課中深入復習，完善體系建構

基于PBL的復習課課堂教學，要求教師精心設計教學環節，努力創設問題情境，從新的視角引發學生新的思考，使其獲得新的體驗，并引導學生不斷深入復習、完善整體建構.在“長方體和正方體的復習”課堂教學中，首先，教師應放手讓有備而來的學生匯報其整理的成果，把展示的空間、提問的權力、評價的機會交給學生，為學生搭建自由發展的舞臺.此時，教師的有效組織與引導至關重要.教師要充分了解不同思維層次的學生復習整理的情況，引導學生進行有序匯報，交流展示小組中最具代表性的知識體系與整理方式.在全班展示交流時，其他學生可以補充不同觀點、質疑或分享自己的新發現[2].再者，教師應根據單元教學中的重難點、疑惑點和關聯點，結合知識體系的深層建構，巧設問題引導與追問，點在關鍵時，導在貫通處.如在“長方體和正方體的體積公式的復習”的課堂教學時設計如下問題：

問題1：對于長方體的體積計算公式，正方體能用嗎？為什么？

問題2：怎樣區分長方體和正方體的體積計算方法？

問題3：三棱柱、五棱柱、圓柱等幾何體的體積可以怎么求？

三個問題驅動學生做好三件事：一、聯結；二、貫通；三、拓展.教師設計精巧恰當的問題串，適時驅動學生對所學知識進行溝通聯系、深入探究，既能使單元知識更具結構化，也能使復習更有層次性、導向性、系統性和延續性.

3.課后拓展應用，提升數學素養

為進一步鞏固知識、提升能力，教師可根據教學內容與現實事物的聯系，設計一些實踐探究性問題，把課堂延伸到課外，讓學生真正地走進生活，適當接觸社會，進而在實踐活動中進一步合作探究、拓展提升[2].在“長方體和正方體的復習”課后，教師可以讓學生參與自家、親朋或學校等場所的裝修，引導學生運用相關知識解決生活中的實際問題，進而提高綜合應用能力和分析解決問題能力.例如，教師創設裝修場所的設計布局、周長面積、體積容積、估算材料、裝修預算等問題情境，以問題驅動學生進行實踐探究、合作交流、互學共進，這既能提升學生的數學綜合學習力，更能助力學生對所學知識的深度理解、學以致用，進而提升數學核心素養.

二、問題導教，助推學生深度建構

《義務教育數學課程標準》指出：“數學教學應注重學生對所學知識的理解，體會數學知識之間的關聯，建構完整的知識體系.[1]”這正是復習課要承載的最重要的教學目標.筆者認為小學數學復習課要達成的是知識體系的建構，要滲透的是方法，要孕育的是思想.教師在復習課教學之前應熟練把握教材，理清知識點間的內在聯系與外在延伸，搭建知識、方法、思想三個維度的頂層設計藍圖.基于PBL的小學數學單元復習課教學，我們以問題為抓手，在建構的過程中將三者深度勾聯，形成一個高質量的結構化課堂架構.下面以“簡易方程的整理與復習”為例，談談課堂教學中教師應如何以問題引導學生深度建構單元知識、方法、思想“三維”體系，進而提高學生的數學核心素養.

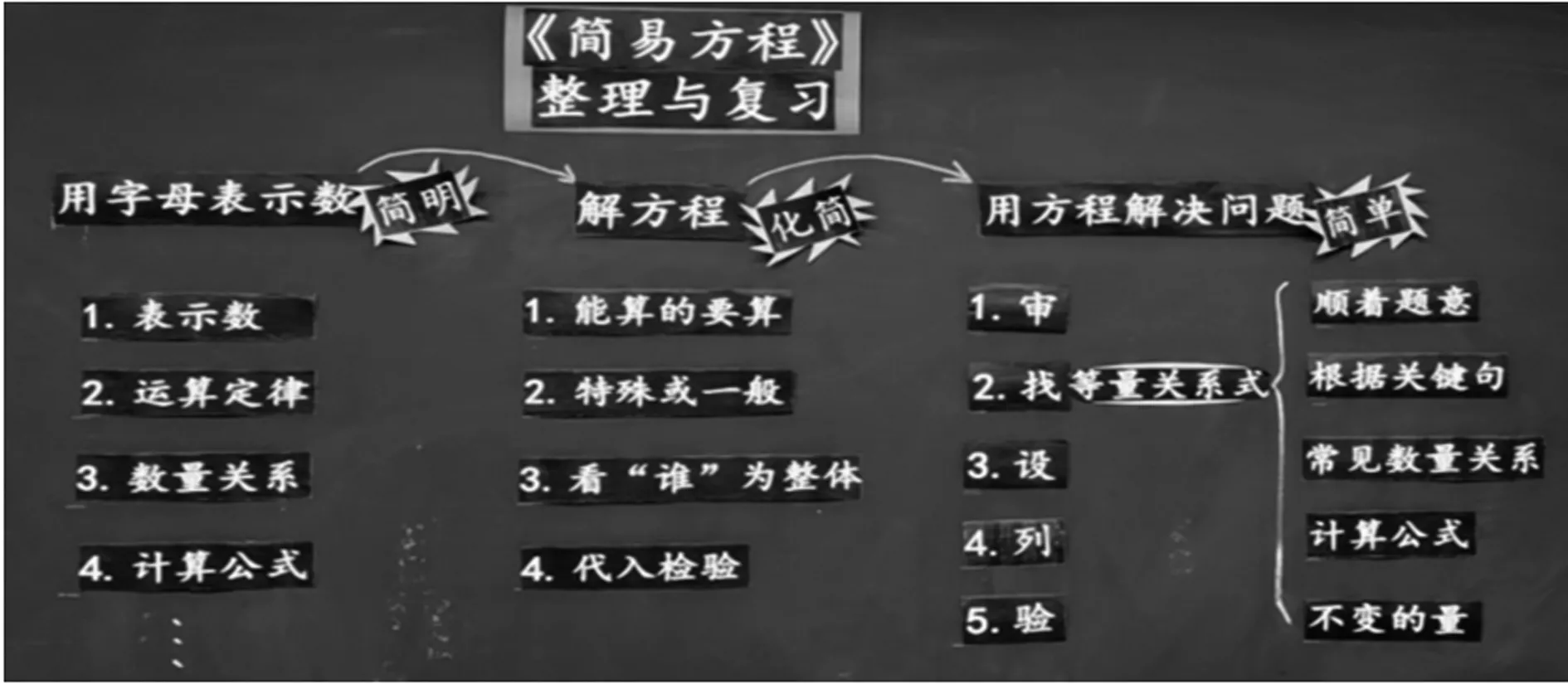
“簡易方程的整理與復習”板書設計

“簡易方程”這單元知識繁雜，但學生在課前整理的基礎上已自主消化基礎知識，建立了基本知識結構.課堂上，教師應根據學情，抓住三條主線，巧設問題串，引導學生深度探究與建構.

1.構建知識體系，立單元復習之架.

著名教育家烏申斯基曾言：“智慧不是別的，只是組織得很好的知識體系.”在引導知識體系的建構時，教師設置的問題應是從大方向到小問題的思維引向，并要處理好橫向豐富與縱向深入的關系.例如：本單元我們學到哪幾部分的知識？(用字母表示數、解方程、用方程解決問題，三部分相互聯系、互為基礎)每部分涉及哪些方面的知識？(根據學生的課前整理與匯報，教師加以引導，并適當補缺補漏，突出重難點)……教師引導學生超越龐雜的知識點，抓住知識間的組織結構和本質聯系，建立完整的單元知識架構.

2.構建方法體系，豐單元復習之軀.

在單元知識體系建構時，教師應適時適當地引導學生理解和把握單元知識背后的本質與規律、方法與策略.例如：本單元復習時，如何用字母表示數？(根據題中數量關系；數字寫在字母前面；乘號省略不寫)解方程時應注意什么？(能算的要先算；當未知數在減數、除數這種特殊位置時，要轉為一般方程，把“誰”看成一個整體；注意代入檢驗)解方程的本質是什么？(不斷化簡解題過程)如何列方程解決問題？(五步)最關鍵的是哪一步？(找等量關系)教師適時地利用問題串層層追問、循循善誘，幫助學生揭示解題規律，總結解題方法，構建更深層次的方法體系，進一步豐富單元復習課的整體建構.

3.構建思想體系，賦單元復習予魂.

隨著培養學生數學核心素養的不斷深入，教師要看到復習課中蘊藏的數學文化、數學思想等方面的價值.例如：本單元在建構知識與方法體系的同時，教師應注意把握時機，以問題引導學生進一步感悟：用字母表示數，其實就是一個“簡化的表達”；解方程，其實就是一個“化簡的過程”；列方程解決問題，其實就是將問題巧妙“簡化成等量關系”，進而解決問題.正如在課尾教師贈予學生的小詩：簡易方程不簡單，知識豐富方法多.簡易方程并不難，化繁為簡克難關.簡易方程是好友，結伴同行助學成.“化繁為簡”的數學思想既是本單元知識學習的方法，也是本單元問題解決的利器，更是今后不斷學習新知的法寶.實踐證明，構建思想體系能打通復習課全身經絡，賦單元復習予靈魂，引導學生實現更高層級的深度建構.

三、問題導評，促進教學深度發展

復習課的評價既是對師生教學成果的肯定，也是對教學過程中所遇問題改進的指引.傳統常規課的評價多以“量”的方式來評價收獲知識的多少，但復習課教學應更講究“質”的評價，重視單元知識的整體建構、深度認知、綜合應用和拓展提升，重視學生的自主學習能力、合作探究意識、高階思維品質的培養等.基于PBL的小學數學單元復習課教學，我們覺得應建立一個以問題為導向、積極有效的評價機制，使“教”的方向明晰，“學”的動力十足，促進教學相長、整體提升、深度發展.

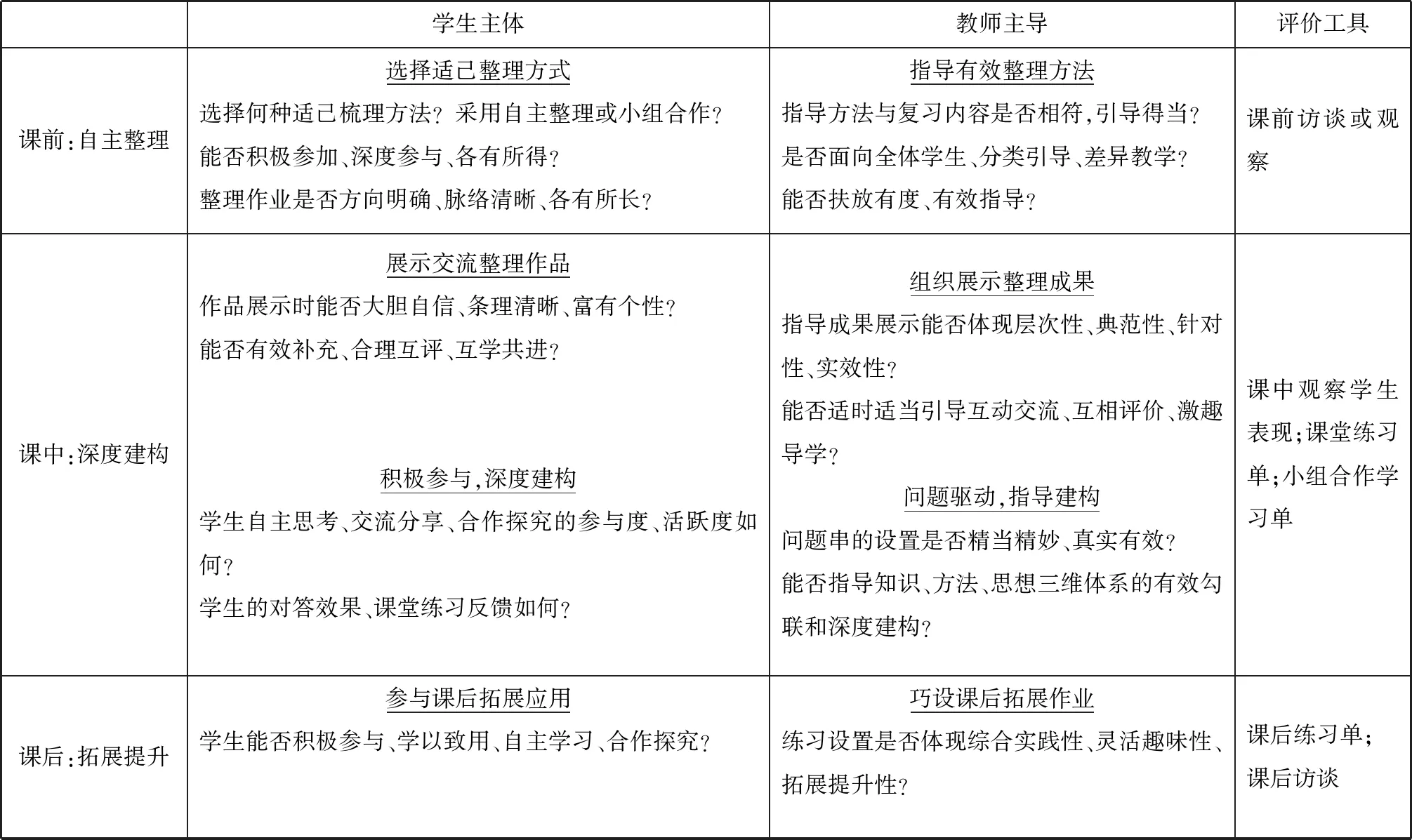
基于PBL的小學數學單元復習課教學評價表

基于“PBL”學.教.評，以問題導學，驅動學生深度參與、引導學生深度學習；以問題導教，要求教師對復習課整體把握、深度設計，強調教師對學生的深度引領、高階建構；以問題導評，讓評價更有針對性、導向性、實效性，進而促進教與學有效開展、深入進行、深度發展.