例析常微分方程在數學建模中的應用
◎陳 杰
(蘇州旅游與財經高等職業技術學校,江蘇 蘇州 215104)
一、引 言
在許多實際問題中,人們常常需要尋求變量之間的函數關系.有時這種關系無法直接建立起來,但是可以建立起該函數的導數所滿足的關系式,這種關系式就是微分方程.微分方程是在處理實際問題中產生的,縱觀微分方程的發展,它與物理、化學、醫學、生物學以及天文學等方面都有著密切的聯系,例如飛行器的運行軌跡,污染物濃度的變化,介質的傳播,傳染病的擴散與控制等都會用到微分方程的理論.
數學建模就是用數學的思想方法對復雜的現象進行分析,并用數學語言描述其中的關系或規律,抽象出恰當的函數關系,將實際問題轉化成數學問題并加以解決.數學建模的過程就是一個分析問題、解決問題的創造性思維過程,也是一個演繹推理與歸納總結相結合的過程,對現實問題的觀察、假設、歸納,怎么將其轉化為一個數學問題是數學建模的關鍵.對于不同的問題可以用不同的方法來建立數學模型,如常見的運動變化率的問題可以利用導數知識來建立模型,常見的抽樣調查問題可以利用統計學知識來建立模型,在研究買彩票中獎的概率的問題可以利用概率論相關知識來建立模型等.
二、常微分方程融入數學建模思想的措施
在日常的常微分方程教學中,教師首先要有意識地培養學生的數學模型思想,善于利用教材中的數學模型作為典型案例進行分析探索.同時在案例素材的選擇上也可以緊緊圍繞學生所學的專業或者是日常生活中最常見的問題,通過學生比較熟悉的案例素材引導學生產生對數學模型建構的認識與理解,讓學生利用常微分方程這個工具去解決專業中或實際生活中的相關問題,這在一定程度上還可以激發學生學習的積極性.其次在日常的常微分方程教學中,教師要有意識地結合數學模型進行案例教學,培養學生將實際問題抽象化成數學模型.這樣可以有效鍛煉學生的數學建模思維能力,提高學生實際問題解決能力.最后教師可采用啟發討論式的教學方法并利用現代信息技術構建數學模型.在數學建模思想融入常微分方程過程中,要引導學生參與到數學建模的各個環節中來,并針對每個環節讓學生展開討論,充分發揮學生的能動性,培養學生自主發現問題并能分析問題、解決問題的能力.教師在教學中也要教會學生利用現代信息技術建立數學模型,這樣可以讓學生對數學建模有更直觀的認識,同時也能簡化模型建立過程中復雜的數值運算.
三、常微分方程在數學建模中的應用
數學建模是聯系數學和實際問題的紐帶,是數學在相關領域被廣泛應用的媒介.數學建模的方法有很多種,而利用微分方程建立數學模型是其中重要的一種.常微分方程可以很好地將實際問題通過數學的語言進行轉化,從而能有效地簡化處理問題的過程,將問題解決.
利用常微分方程解決實際問題一般可按如下步驟進行:首先,用數學符號假設出實際問題中所涉及的變量和變化率,找出問題中包含的原理以及相關公式、定理等,根據問題的規律列出相應的微分方程;其次,對微分方程進行求解或對方程進行進一步的定性分析.對于參數問題模型需進一步討論參數變化對于問題的影響;最后,對結果進行描述、分析、預測或控制.下面從日常生活、幾何、物理以及經濟等方面常見例子來介紹微分方程在數學建模中的廣泛應用.
(一)日常生活方面的應用
日常生活中的很多問題都可以建立數學模型,并利用常微分方程進行解決.下面以日常交通出行中最常見的紅綠燈問題以及生活中經常出現的溶液稀釋問題為例,介紹常微分方程在數學建模中的應用.
例1(紅綠燈問題):在一些大城市中,由于汽車保有量比較大,等紅綠燈時的擁堵一直是一個比較麻煩的問題.在紅綠燈轉換的過程中通常會有個過渡狀態的黃燈.怎么合理的設置紅綠燈的時間,即能保證交通安全又能避免由于車輛積壓造成等候時間過長,給司機和乘客造成煩惱,如何設置黃燈閃爍的時長,是交通指揮燈經常要處理的問題.

例2(溶液稀釋問題):假設現有一批工業鹽溶液,每升溶液中含0.3 kg的工業鹽,現以2 L/min的速度將溶液倒入裝有10 L純凈水的容器中,溶液在容器里經過稀釋后又以相同的速度從容器中流出,問經過5 min后,容器中還剩有多少工業鹽.
解:令時間t為函數的自變量,把注入容器經過t分鐘時工業鹽的數量看作待求解的未知函數y(t),接下來求t到t+Δt這段時間間隔內工業鹽的變化量.
流入:2ΔtL溶液中含有0.3·2Δt=0.6Δtkg的工業鹽.

于是,在這段時間內工業鹽的增量為y(t+Δt)-y(t)=0.6(Δt-0.2)Δt(y(t)+α),上式除以Δt,當Δt→0時求極限,可得微分方程y′(t)=0.6-0.2y(t).
求通解得y(t)=3+Ce-0.2t,而y(0)=0,代入上式求得特解為y(t)=3-3e-0.2t.
所以,當t=5時,容器中將有y(5)=3-3e-0.2×5=3e-1≈1.9 kg的工業鹽.
在上例中主要體現了數學建模的思想,在實例中,引入了時間變量,建立了微分方程模型,通過求其特解,進而求得其結果.
(二)幾何方面的應用
常微分方程還可建立求解幾何問題的數學模型,主要利用導數的幾何意義,即函數y=f(x)的導數y′等于函數所表示曲線上點(x,f(x))處切線的斜率.
例1已知一條曲線通過點(1,3),且曲線上任何一點(x,y)處切線介于x軸及y=x+1之間的線段正好被切點所平分,求該曲線的方程.
解:設該曲線的表示式為y=y(x),則過任意點(x,y)的切線方程可表示為:
Y-y=y′(X-x)
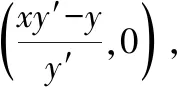

這是一個一階線性方程,通過計算可得曲線的方程為:
y2-xy-y=3.
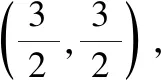
解:設點N的坐標為(x,y),則切線NA的方程為Y-y=y′(X-x).令X=0,則Y=y-xy′,故點A的坐標為(0,y-xy′).



(三)物理方面的應用
微分方程物理應用的范圍很廣,幾乎涉及物理學的每個分支,但應用得較多的領域是動力學及電學.在動力學中主要用牛頓第二定律,在電路分析中主要用克西霍夫定律.
例1從地球表面垂直向上發射一枚質量為m的火箭,考慮火箭所受空氣阻力可忽略不計的理想狀態,設火箭初速為v0,求火箭能克服地球引力發射到無窮遠去的最小速度.

這時一個形如y″=f(y,y′)不顯含自變量的二階微分方程,可降階為一階微分方程.



例2在RLC串聯電路中串接交流電源E0sinωt,求回路電流i(t).

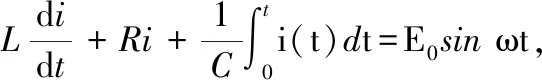



當ω≠ω0時,非齊次方程(1)的通解為

由解得結果分析可知,當ω≠ω0時,回路電流i(t)是一個周期振蕩的電流;當ω=ω0時,由于特解中含有tsinω0t項,當t→∞時振幅可趨于無窮,這就是共振現象.
(四)經濟學方面的應用
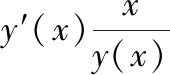
例1(人口模型)某城市在時刻t的人口函數用p=p(t)表示,m及n分別表示該城市的出生率和死亡率,在時間段Δt內出生人口與死亡人口都與Δt成正比.求在不發生意外的情況下,該城市的人口函數.
解:考慮在時間段[t,Δt]內人口的變化:(m-n)應表示人口的自然增長率,一方面,(m-n)p(t)Δt應近似表示這個時間段內人口的變化;另一方面,Δp=p(t+Δt)-p(t)精確表示了這個時間段內人口的變化,由此Δp≈(m-n)p(t)Δt.

注:生物群體的生滅變化是一個隨機過程,本例給出的只是一個簡化的近似模型.
例2(房貸模型)某客戶向銀行申請住房貸款,貸款本金為y0=20萬元,貸款月利率為λ=0.0045,協議貸款時間為300個月,問該客戶平均每月應向銀行還貸本息為多少.(銀行利息需計復利)
解:記y(k)為第k個月還款后尚欠銀行的本息數,x為每月還貸金額(為常數),則可建立方程y(k+1)=(1+λ)y(k)-x,初始條件為y(0)=y0,這時線性差分方程的初值問題:
通過求解可得x=1216.26元.






四、結束語
常微分方程在數學建模中的廣泛應用,將數學理論方法與實際生活巧妙地結合了起來,將生產生活實際中不容易解決的難題用數學的方法解決.常微分方程建立起來的數學模型,一般都是動態的數學模型,雖然整個推導過程相當復雜,但是結果卻是簡單明了.因此,將常微分方程和數學建模有機結合起來,能夠讓常微分方程在實際應用過程中發揮更大的作用,解決更多的實際問題.

