速度脈沖地震下偏心重力柱-核心筒結構的彈塑性地震響應分析

馬曉宇，補國斌，熊浩然，徐 沖，汪 恒，張 哲

（湖南工業大學 土木工程學院，湖南 株洲 412007）

0 引言

近年來，偏心建筑結構發展迅速，其抗震研究和應用也得到了快速發展。國內外專家學者們對偏心結構的抗震性能進行了廣泛的研究。如Bu G.B.等[1]對強度偏心框架結構的地震易損性進行了分析。夏玲濤等[2]對雙向偏心結構實用抗震計算方法進行了研究。補國斌[3]針對偏心框架結構體系的抗震性能和設計方法展開了詳細研究。但是已有研究大多數是針對傳統結構體系進行的研究。雖然周靖等[4]提出了一個新型重力柱-核心筒結構體系，并開展了相關的地震模擬振動臺試驗研究和數值分析，但是尚未對其偏心體系展開進一步分析。因此，本研究將以此新型重力柱-核心筒結構為研究對象，開展其在偏心布置下的抗震性能研究。

歷次震害分析結果表明，相對于非速度脈沖型地震動，速度脈沖型地震動對結構產生的影響更強，更易使建筑物倒塌和破壞。國內外大量的研究結果表明，結構在速度脈沖地震下的層間剪力、位移和延性需求等動力響應較非脈沖情況的顯著增大[5]。但是大多數有關速度脈沖地震的研究均停留在對規則和對稱結構的研究上，而考慮速度脈沖地震效應和偏心綜合影響的研究較少[6]，且尚無考慮速度脈沖地震和偏心雙重不利因素對新型重力柱-核心筒結構體系抗震性能影響研究的報道。

針對已有研究中的不足，本研究主要考慮在速度脈沖地震與結構質量偏心雙重不利條件下，新型重力柱-核心筒結構的彈塑性地震響應變化規律，重點探討雙重不利條件對頂點位移、層間剪力、層間位移和層間扭矩及扭轉角的定量影響規律。

1 偏心重力柱-核心筒結構模型

1.1 重力柱-核心筒結構振動臺試驗簡介和數值模擬

新型重力柱-核心筒結構體系利用核心筒具有的抗側、抗扭剛度大的優勢，將結構外圍框架柱、內筒剪力墻與鋼梁的連接節點由剛接改為鉸接，將外框架設計成只承受重力荷載的重力柱，而水平荷載由核心筒承擔，這樣能使結構受力更明確，不用糾結外框架剪力比的調整，簡化設計過程、提高結構設計的靈活性。新型體系極大地減少了施工現場的焊接工作量，有半工業模塊化建造特點，為建筑結構形式創新提供了靈活性。

文獻[4]以混凝土重力柱-核心筒結構的實際工程——廣西金融大廈為背景，開展了1:50 縮尺地震模擬振動臺試驗研究（其結構模型見圖1），結構構件典型的損傷情況如圖2所示，試驗模型和數據的詳細介紹參見文獻[4]，本文從略。

圖1 振動臺試驗結構模型Fig.1 Structural model of the shaking table test

圖2 典型構件損傷情況示意圖Fig.2 Schematic diagram of typical component damages

本研究以該試驗對應的原型結構為基礎開展研究。原型結構的總高度為320 m，共37 層，其他構件配筋、荷載條件、地震輸入等詳細信息參見文獻[7]。并采用李康寧博士開發的結構靜動力非線性分析軟件CANNY[8]對結構進行地震響應分析。CANNY 軟件使用有限元、線單元和特殊單元表達結構的力學特性，基于塑性理論建立單元力和變形關系，采用數值積分逐步求解法模擬結構物在各種靜力/動力荷載作用下變形、損傷和破壞的全過程。關于CANNY 軟件更詳細的介紹，參見文獻[8]。

采用CANNY 軟件對原型結構進行數值建模，得到如圖3所示的有限元模型。

圖3 結構的CANNY 有限元模型Fig.3 Finite element model of CANNY of the structure

本研究中，選用的混凝土強度等級為C60，鋼筋級別為HRB335 和HRB400，詳細參數等見文獻[7]。鋼筋和混凝土的本構關系模型分別采用CANNY 中的SR4 模型和CS4 模型進行表達，材料參數的符號說明詳見文獻[8]，參數取值采用程序建議的默認值（材料本構關系模型如圖4所示）。將試驗用地震波按相似比轉換為原型結構的地震記錄，并作為地震動輸入，對該原型結構進行非線性動力時程分析，得到模擬結果。然后對模型試驗結果按相似比轉換為原型試驗結果。選取7 度小震、中震和大震數據進行對比分析，所得結果如圖5所示。由圖5可以得知，模擬結果和試驗結果吻合度較高，表明建模和參數設置合理，故可以采用同樣的參數設置進行下文的數值擴展參數化分析。

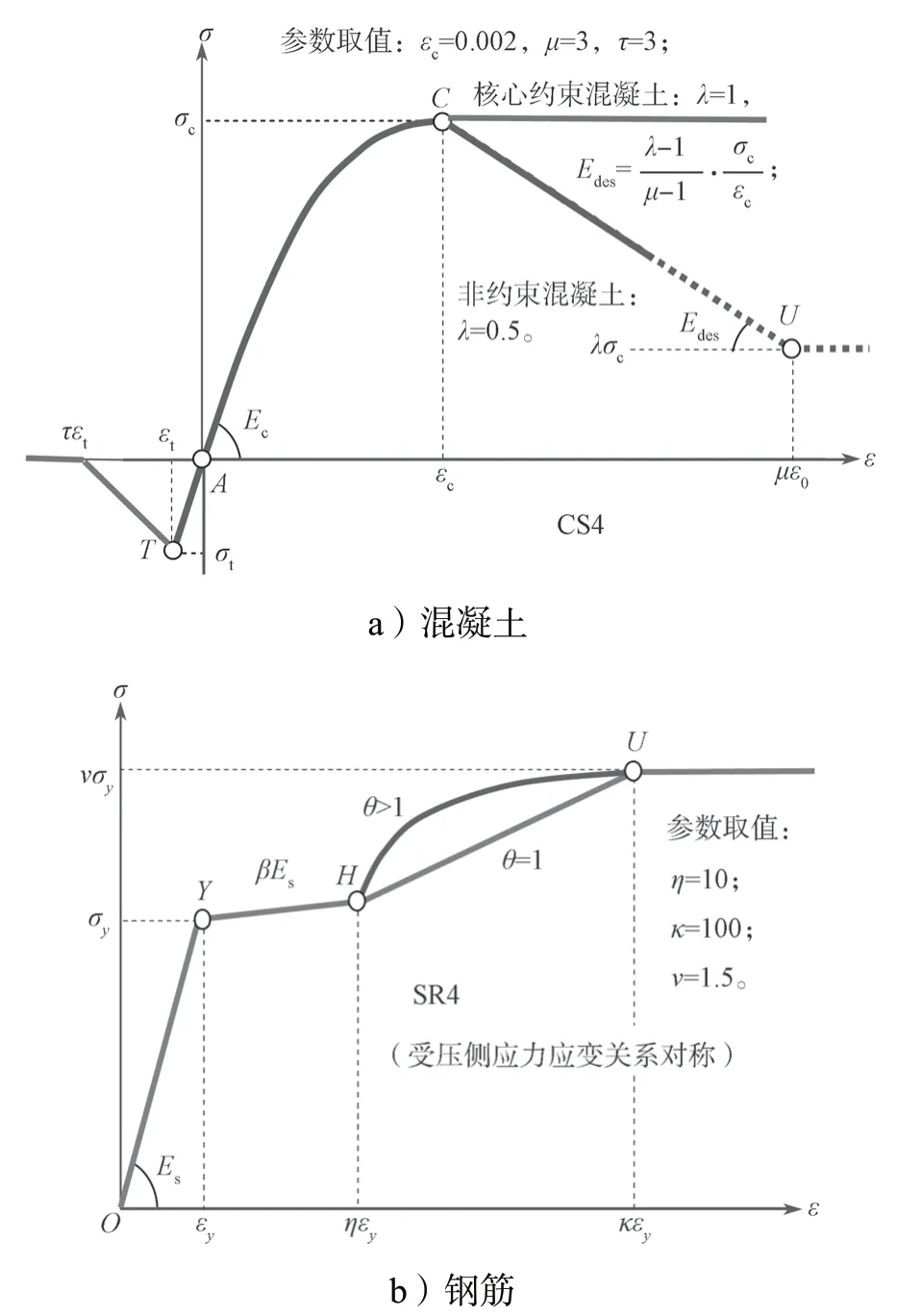
圖4 材料的本構關系模型Fig.4 Material constitutive relation model

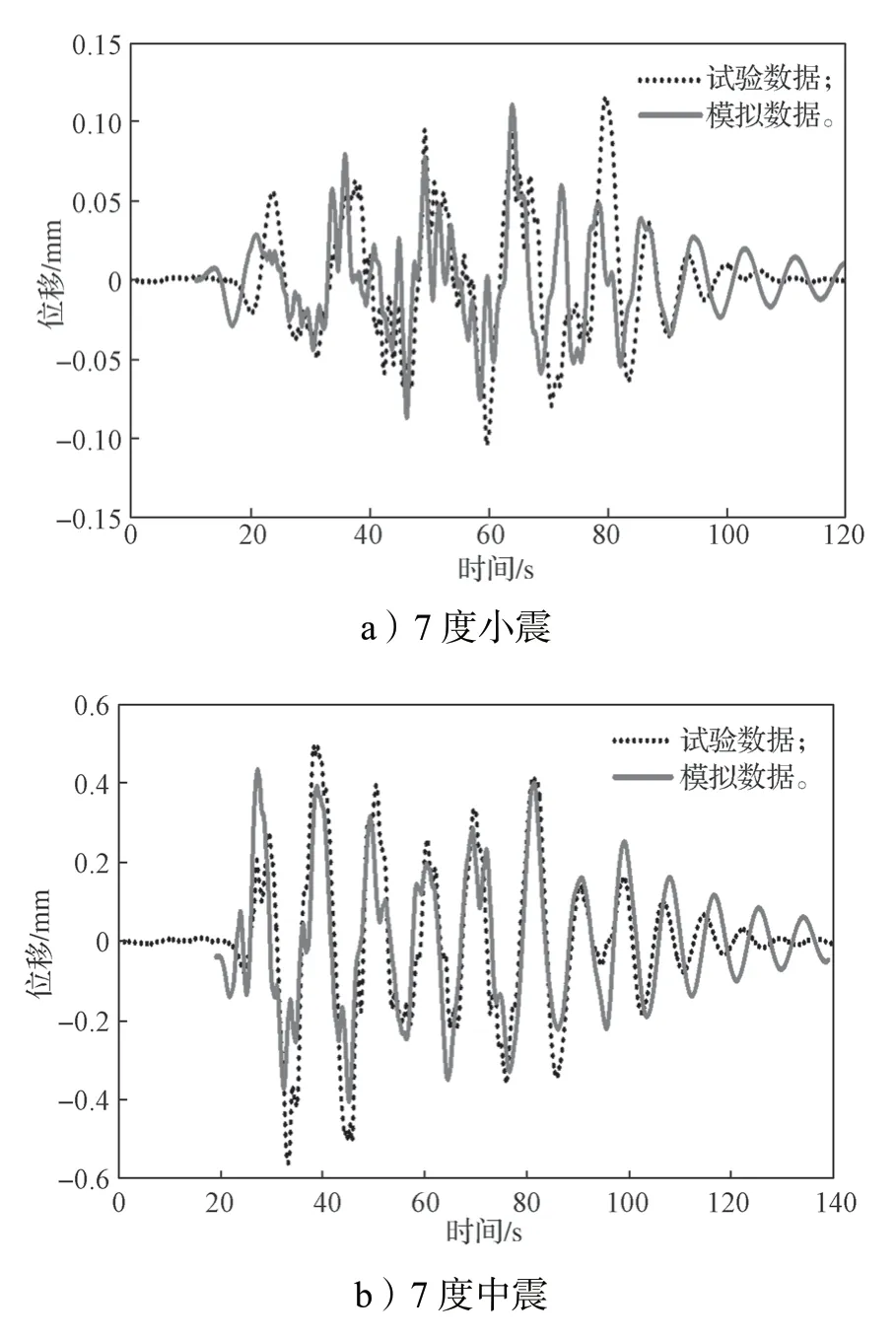
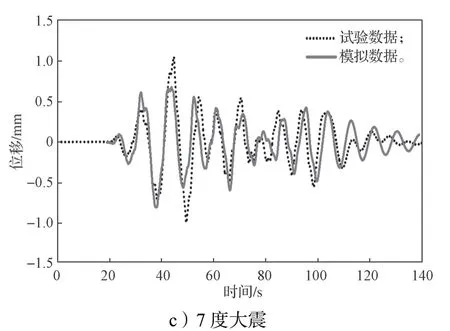
圖5 不同震級下的位移時程比較Fig.5 Comparison of displacement time history under different earthquake magnitudes

1.2 偏心重力柱-核心筒結構建模

以上文給出的新型重力柱-核心筒結構為基準結構，通過調整左右側質量，得到偏心體系，圖6為對稱結構與偏心結構的平面示意圖。

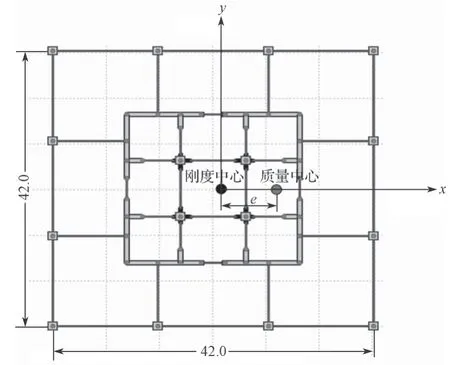
圖6 對稱結構與偏心結構平面示意圖Fig.6 Plane diagram of symmetric and eccentric structure

本模型分析中僅考慮沿x軸單向偏心（因結構對稱，沿y軸單向偏心情況與x軸相同），即左側各節點的質量減小，右側各節點的質量增大，但調整后結構的總質量保持不變。結構偏心率的計算公式如下：

式中：xi為第i根柱或者墻質心相對于幾何中心的橫坐標；

L為結構沿偏心方向的總長度；

e為質量偏心距。

前期研究結果表明[3]，在豎向布置上，各層均勻偏心體系相對于其它偏心體系的地震需求更大，更為不利，所以本研究選取各層均勻質量偏心體系來進行研究與分析。

2 地震動輸入與分析方法

2.1 地震動輸入

歷次震害表明，速度脈沖地震作用相對于非速度脈沖地震作用，將對結構造成更大的速度和位移沖擊。選取表1所列3 條近場速度脈沖型地震加速度記錄，編號P1~P3，速度脈沖特性用基于速度和能量標定的脈沖指標（PI）[9]表征。同時，選取對應的3 條非速度脈沖記錄作為對比，編號為N1~N3，詳細的地震記錄數據參見文獻[9]，此處不再列出。為強調地震作用的隨機性和不確定性，表中所列內容均采用原始加速度記錄。

表1 選取的3 條速度脈沖型地震動記錄Table 1 Three selected velocity pulse ground motion records

2.2 分析方法

結合前期振動臺試驗數據，綜合考慮速度脈沖強震和結構偏心耦合效應，對偏心重力柱-核心筒結構體系進行彈塑性地震響應演化規律分析。

基于1.2 節的結構模型和2.1 節的地震動記錄，采用CANNY 程序，依據以下條件進行非線性動力時程分析：4 種偏心率（0, 0.1, 0.2, 0.3 分別代表無偏心，小、中、大偏心程度）；6 條地震加速度記錄（3條速度脈沖型地震和對應的非速度脈沖型地震）。地震作用為y軸方向，偏心沿x軸方向。峰值地面運動加速度取0.5g，保證各結構模型均進入彈塑性受力階段和變形階段。

3 彈塑性地震響應分析

分析結果表明，脈沖工況和非脈沖工況下，各條地震波下得到的規律具有一致性。因此，3.1 節僅以脈沖和非脈沖的第一條地震波為例進行分析和對比，其他工況規律類似。3.2 至3.3 節則采用兩種地震工況下3 條地震波得到的計算結果平均值來表征結構的整體地震響應。以下各圖中 “P”和“N”分別表示速度脈沖地震工況和非速度脈沖地震工況（以下分別簡稱脈沖工況和非脈沖工況）。“e”表示偏心率，圖中“P1-e=0”表示第一條速度脈沖地震工況下偏心率為0 時的曲線。

3.1 單條地震波作用下的頂點位移時程分析

圖7分別給出了P1 與N1 工況下不同偏心率結構的頂點位移時程變化曲線。

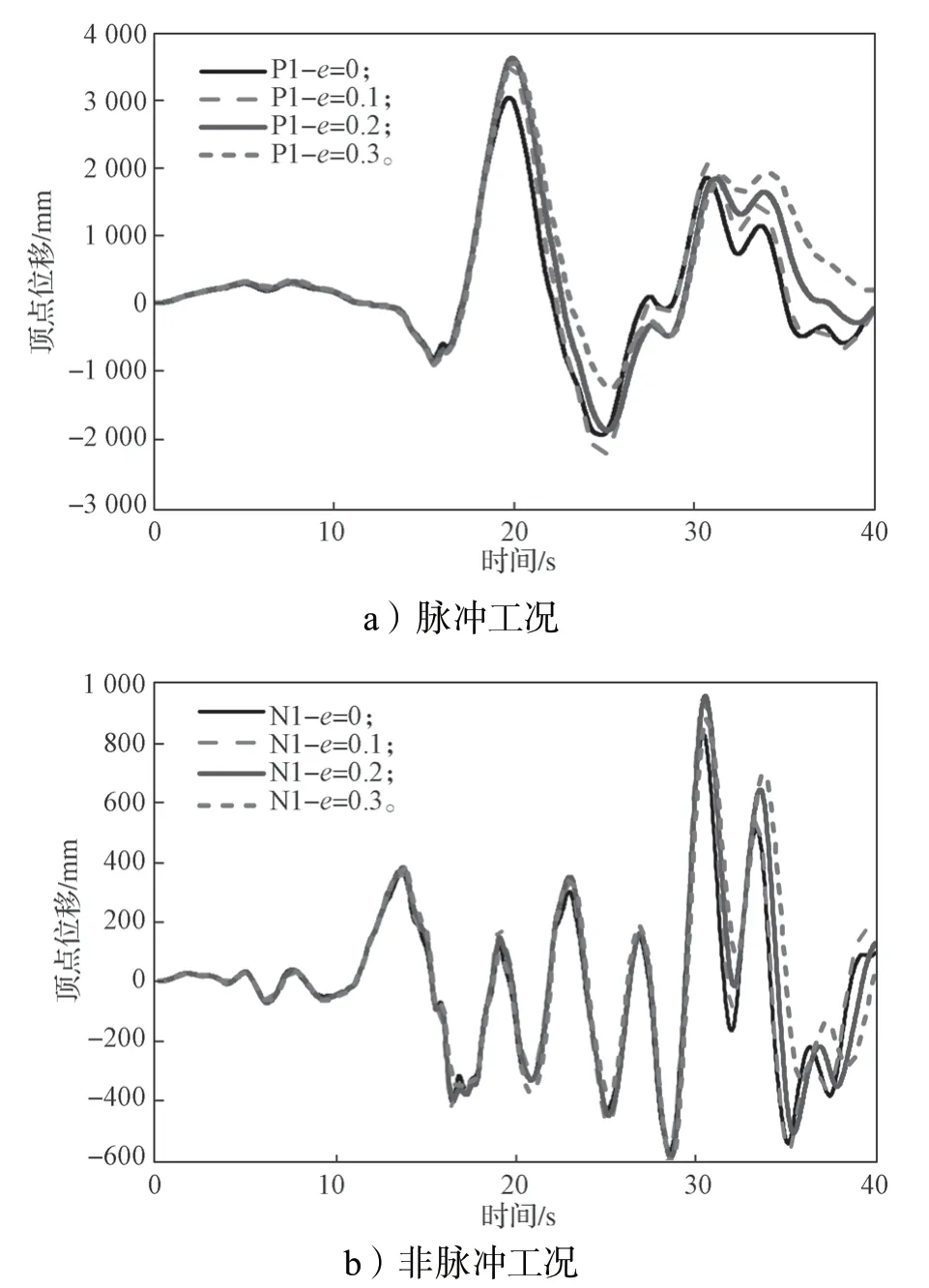
圖7 不同工況下各結構的頂點位移時程曲線Fig.7 Vertex displacement time history curves of the tube structures under different conditions

由圖7可知，同一時間的頂點位移最大值隨著偏心率增大表現出增大的變化趨勢。這一現象表明，偏心率越大，對結構頂點位移的影響也越大。此外，通過兩工況下的曲線對比可以看出，在脈沖工況下，結構的最大頂點位移接近4 000 mm，而非速度脈沖工況下的最大頂點位移僅接近1 000 mm，約為速度脈沖工況下的1/4。由此可以得知，速度脈沖型地震對結構頂點位移的影響要遠大于非速度脈沖型地震對結構頂點位移的影響。

3.2 偏心和速度脈沖效應對最大層間剪力和最大層間位移角的影響

非線性動力時程分析所得偏心率和速度脈沖效應對最大層間剪力的影響曲線如圖8所示，其中圖8a 為脈沖和非脈沖工況下，不同偏心率結構各樓層最大層間剪力的變化規律。

觀察圖8a 中的曲線可知，兩種地震工況下，各層的層間剪力包絡線均隨著偏心率的增大有內收的變化趨勢。此規律與文獻[10]的結論類似。可能的原因是隨著偏心率增大，扭轉效應加大，與地震輸入垂直的另一方向也隨之分擔了部分剪力作用，導致沿地震方向的層間剪力減小。另外，當偏心率相同時，脈沖工況下各樓層的層間剪力包絡線位于非脈沖工況下包絡線以外。

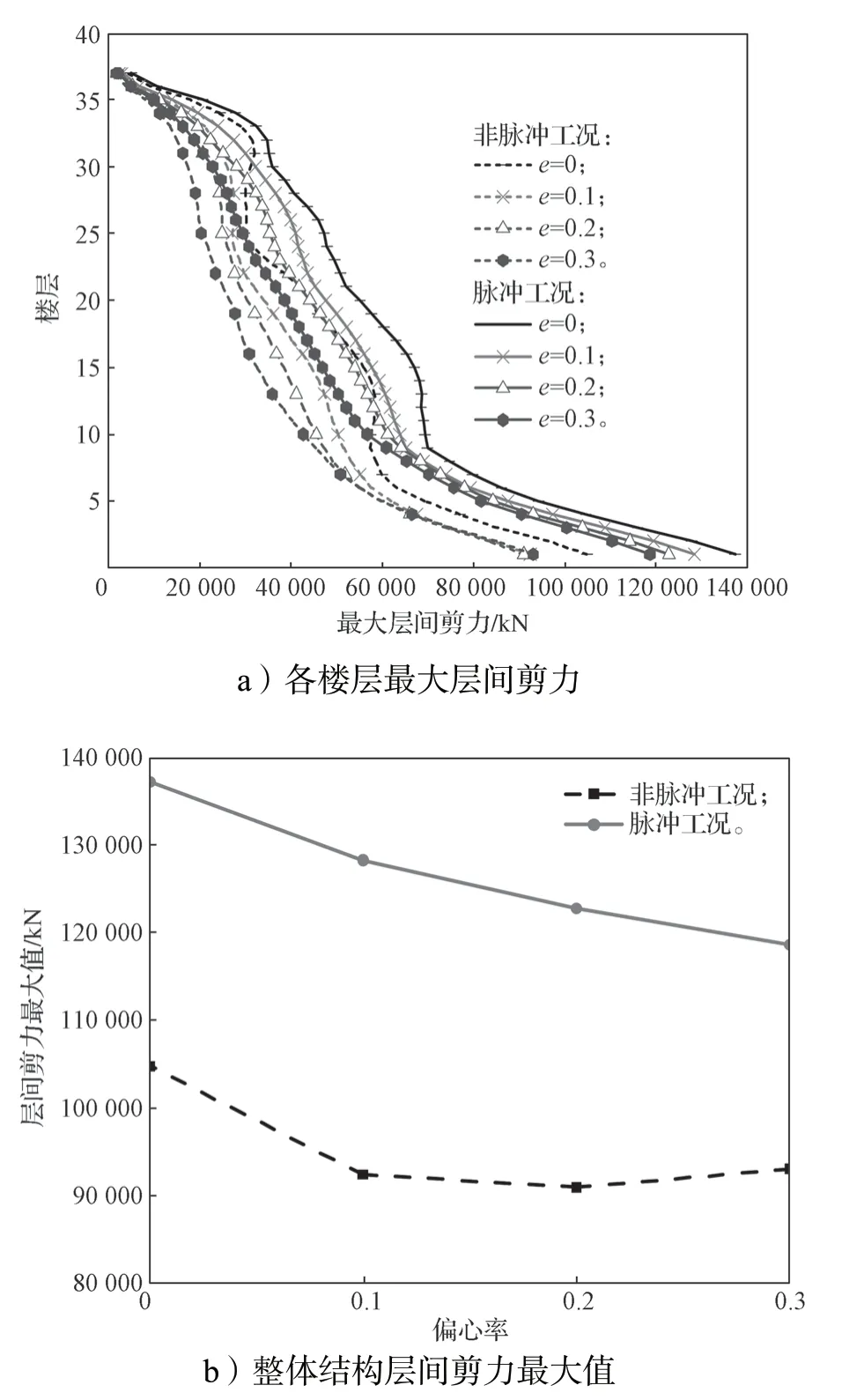
圖8 不同工況下的最大層間剪力變化規律曲線Fig.8 Change trend curves of the maximun inter-story shear force under different conditions

為了定量分析偏心率和速度脈沖地震效應的影響，進一步給出了整體結構最大層間剪力值（取各樓層最大層間剪力的最大值）隨偏心率的變化規律，如圖8b 所示。

由圖8b 中的曲線可以得知，兩種地震工況下，整體結構的層間剪力最大值均隨偏心率增大有減小的變化趨勢。當偏心率由0 變為0.3 時，脈沖工況和非脈沖工況下的最大層間剪力值分別減小了15%和17%。而偏心率一定時，脈沖工況下的整體結構最大層間剪力值顯著高于非脈沖工況下的對應值。如當偏心率均為0.1 時，脈沖工況下的層間剪力約是非脈沖工況下層間剪力的1.4 倍。

非線性動力時程分析所得偏心率和速度脈沖效應對最大層間位移角影響的規律曲線如圖9所示。其中，圖9a 表示不同偏心率下，結構在脈沖和非脈沖工況下各樓層最大層間位移角的變化規律曲線；圖9b 為取各條曲線的層間位移角的最大值進行定量分析所得的變化規律曲線。

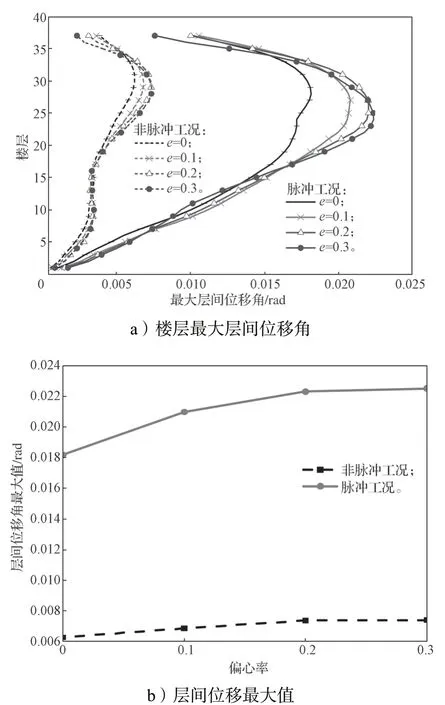
圖9 不同工況下的層間位移角變化規律曲線Fig.9 Change trend curves of the inter-story drift ratios under different conditions

從圖9a 所示樓層最大層間位移角變化曲線可以看出，在脈沖和非脈沖兩種工況下，樓層最大層間位移角隨著偏心率增大有增大的變化趨勢。此外，脈沖工況下的最大層間位移角要遠大于非脈沖工況下的。由圖9b 可以得知，在脈沖和非脈沖兩種工況下，樓層層間位移角的最大值均隨著偏心率增大有增大的變化趨勢，當偏心率由0 變化到0.3 時，脈沖工況和非脈沖工況下的最大層間位移角分別增大了24%和18%。另外，在相同偏心率條件下，脈沖工況下的最大層間位移角明顯遠大于非脈沖工況下的。如當偏心率為0.1 時，脈沖工況下的層間位移角最大值約是非脈沖工況下的3 倍。

3.3 偏心和速度脈沖效應對最大層間扭矩和最大層間扭轉角的影響

非線性動力時程分析所得偏心和速度脈沖效應對最大層間扭矩的影響結果如圖10 所示。其中，圖10a 是不同偏心率下，結構在脈沖和非脈沖工況下各樓層間扭矩值的變化曲線，圖10b 為提取各工況下整體結構的層間扭矩最大值分析曲線。

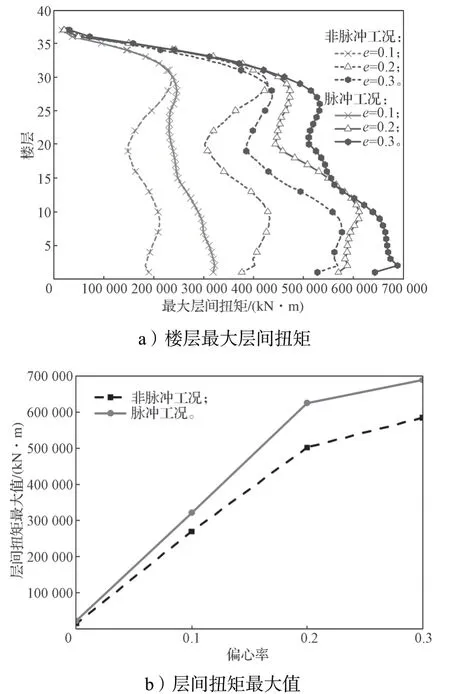
圖10 不同工況下的層間扭矩變化規律曲線Fig.10 Change trend curves of the inter-story torsion under different conditions

由圖10a 中的樓層最大層間扭矩曲線可看出，在所有工況下，最大層間扭矩均隨偏心率的增大而減小，最大層間扭矩值均在靠近底部出現。由圖10b可知，在同種工況下，隨著偏心率增大，層間扭矩最大值隨之增大，且呈現先線性急劇增長后非線性緩慢增長的發展趨勢。這是由于隨著偏心率增大，扭轉效應加大，出現了耦聯現象。同時，在其余條件相同的情況下，脈沖工況的層間扭矩比非脈沖工況大。如偏心率為0.3 的情況下，脈沖工況下的底層扭矩約為非脈沖工況下的1.2 倍。

非線性動力時程分析所得偏心率和速度脈沖效應對最大層間扭轉角的影響結果如圖11 所示。其中圖11a 為不同偏心率下，結構在脈沖工況和非脈沖工況下各樓層最大層間扭轉角的變化曲線，圖11b 為各工況下整體結構層間扭轉角最大值變化曲線。

圖11 不同工況下的層間扭轉角變化規律曲線Fig.11 Change trend curves of the inter-story rotation under different conditions

由圖11a 可以看出，最大層間扭轉角的變化規律與最大層間位移角的變化規律類似，但是其最大值出現在結構頂部附近。由圖11a 還可以得知，各樓層最大層間扭轉角隨著偏心率增大而增大，脈沖工況下的包絡曲線明顯比非脈沖工況下的外擴。由圖11b 可知，當偏心率相同時，脈沖工況下的層間扭轉角最大值明顯大于非脈沖工況下的。如當偏心率為0.3 時，脈沖工況下的最大層間扭轉角是非脈沖工況下的2.8 倍左右。此外，同種工況下，層間扭轉角最大值隨著偏心率的增大不斷增大，且增幅較大，總體上呈現出線性增長的變化趨勢。

4 結論

通過對重力柱-核心筒結構在速度脈沖地震和偏心耦合條件下的地震響應分析，得到以下主要結論：

1）重力柱-核心筒結構的頂點位移隨著偏心率的加大有增大的變化趨勢，速度脈沖地震作用下（脈沖工況）的頂點位移極值遠高于非速度脈沖地震下（非脈沖工況）的對應值。脈沖工況的頂點位移極值約為非脈沖工況的4 倍。故對結構的彈塑性分析中，應重點關注速度脈沖地震效應。

2）各樓層最大層間剪力隨著偏心率的增加而減小，而各層間位移角則表現出相反的變化趨勢。脈沖工況和非脈沖工況下，當偏心率由0 變化到0.3 時，層間剪力最大值分別減小了15%和17%，最大層間位移角分別增大了24%和18%。當偏心率一定時，脈沖工況下的層間剪力最大值和層間位移角最大值均顯著高于非脈沖工況下的對應值。當偏心率為0.1時，脈沖工況下的層間剪力最大值和層間位移角最大值分別是非脈沖工況下層間位移的1.4 倍和3.0 倍。因此，速度脈沖地震作用下，位移的增大效應比力的增大效應更為明顯。

3）各樓層最大層間扭矩和最大層間扭轉角均隨著偏心率的增加而增大。隨著偏心率加大，層間扭矩最大值表現出先線性增長后非線性增長的變化趨勢，層間扭轉角最大值則表現出大致成線性增長的變化趨勢。當偏心率一定時，脈沖工況下的層間扭矩最大值和層間扭轉角最大值均顯著高于非脈沖工況下的對應值。如當偏心率為0.3 時，脈沖工況下的層間扭矩最大值和層間扭轉角最大值分別是非脈沖工況下的1.2 倍和2.8 倍。