基于神經網絡的LCL型并網逆變器控制策略

屈浩軒，陳 剛，董和夫，李江坪，喬超杰，虞佳興

（湖南工業大學 電氣與信息工程學院，湖南 株洲 412007）

0 引言

為解決能源危機和生態環境問題，人們將目光轉移到開發新型清潔能源上，光伏發電應運而生[1]。光伏發電是利用半導體材料的光生伏特效應進能量轉換，逆變器是整個系統的重要組成部分[2]。由于受到光照強度和環境溫度等不穩定因素的影響，以及電力電子裝置的廣泛應用，電網將會被注入大量諧波，造成電網波動，降低電能質量[3]。因此，要改進并網逆變器的濾波效果，提升并網電流的跟蹤性能[4]。

改進并網逆變器的濾波效果主要采用電容電流反饋有源阻尼法，其優點為阻尼效果好、簡單易行、實用性強等[5]。對于LCL 型并網逆變器的電流內環控制方式有PI（proportional integral）控制、PID（proportional-integral-derivative）控制和神經網絡控制等。其中PI 控制結構簡單、穩定性好，但需要建立精確的系統模型[6]。PID 控制魯棒性和適應性較強，但傳統的PID 控制對非線性系統難以達到理想的控制效果，有著明顯的局限性[7]。其參數是通過人們的工作經驗設定，通常是固定不變的，在光伏發電系統的工作環境改變時，由于控制器無法及時調整出合適的控制參數，造成并網電流跟蹤精度降低。神經計算是一種參照生物神經系統信息處理的數學模型，具有自適應學習能力、容錯性高和抗干擾能力強等優點。BP 神經網絡使用多層網絡學習算法，具有逼近任意非線性函數的能力，因此被廣泛應用于控制領域[8]。

基于上述分析，利用電容電流反饋有源阻尼方法和BP（back propagation）神經網絡控制技術的優點，提出了BP 神經網絡結合PID 控制的策略，并運用到單相LCL 型并網逆變器的并網電流控制之中。為驗證理論正確性進行了實驗仿真，結果表明該策略能夠實時調整PID 參數，實現對并網電流跟蹤。

1 LCL 型并網逆變器介紹

單相LCL 型并網逆變器主電路如圖1所示。

圖1 單相LCL 型全橋并網逆變器主電路Fig.1 Main circuit of single-phase LCL full-bridge grid-connected inverter

圖1中，Ud為光伏直流電壓，逆變橋的兩個橋臂分別由MOS 管Q1和Q2、Q3和Q4構成，其中Q1和Q2互補工作，Q3和Q4互補工作，4 個MOS 管的通斷采用雙極性SPWM（sinusoidal pulse width modulation）進行控制。Uin為逆變橋電路輸出電壓，單相LCL 濾波器由電感L1、L2和電容C構成，其中電容C為高頻諧波電流提供了通路。i1為逆變橋電路輸出電流，i2為并網側電流，UC為濾波電容兩端電壓，Ug為并網側兩端電壓。

根據圖1可列出如式（1）所示方程組：

式中 ：j 為虛數單位；uin(t)為時域上的逆變橋電路輸出電壓；uC(t)為時域上的電容電壓；ug(t)為時域上的并網電壓；ω為電網角頻率。

對式（1）進行拉普拉斯變換，可得

單相LCL 型并網逆變器結構框圖如圖2所示。

圖2 單相LCL 型并網逆變器的結構框圖Fig.2 Structure block diagram of single-phase LCL typed grid-connected inverter

圖2中KPWM=Vin/Vtri，Vin為調制波的幅值，Vtri為三角載波的幅值。單相LCL 型并網逆變器控制結構圖如圖3所示。

圖3 單相LCL 型并網逆變器控制結構圖Fig.3 Control structure diagram of single-phase LCL typed grid-connected inverter

由于LCL 濾波器存在諧振尖峰，會造成電力系統不穩定，需要在諧振頻率處進行阻尼[9]。電容電流反饋有緣阻尼法實現簡單、阻尼效果好，因此采用電容電流比例反饋的控制方式。

圖中Hi1為濾波電容電流iC的反饋系數，用于實現LCL 濾波器諧振尖峰的電容電流反饋有源阻尼，Hi2為并網側電流i2的采樣系數，HV為并網側兩端電壓Ug的采樣系數。通過PLL 鎖相環獲得采樣電壓Ug的相位，并將相位賦予給定值Iref得到指令電流iref，iref與并網側電流的采樣信號i2進行比較，得到誤差信號送入電流調節器Gi(s)輸出Ur。Ur減去電容電流iC的反饋信號UiC輸出調制波UM，最后由SPWM 調制控制逆變電路的開關管通斷，完成并網電流閉環控制。經上述分析可繪制出含電容電流反饋有源阻尼的單相LCL 型并網逆變器結構框圖，如圖4所示。

圖4 含電容電流反饋有源阻尼的單相LCL 型并網逆變器結構框圖Fig.4 Block diagram of single-phase LCL typed grid-connected inverter with an active damping of capacitor current feedback

2 BP 神經網絡PID 控制器

2.1 BP 神經網絡介紹

BP 神經網絡結構分為3 部分：輸入層、隱含層、輸出層，層與層之間由權值矩陣連接，隱含層中的大量神經元用于計算處理[10]。BP 神經網絡結構如圖5所示。

圖5 BP 神經網絡結構Fig.5 BP neural network structure

2.2 BP 神經網絡學習

確定BP 神經網絡結構，設置學習率、隱含層層數、輸入和輸出向量元素個數、隱含層神經元個數、各層激活函數、層間初始權值矩陣、學習率、遺忘因子及學習算法。完成結構設計后進入學習階段。

BP 神經網絡學習由兩個階段組成：第一個階段為BP 神經網絡的前向傳播，輸入向量通過權值矩陣從輸入層傳遞到隱含層的各個神經元中，神經元經過本層的激活函數計算將結果傳遞至下一層，下一層再向后一層不斷計算和傳遞，直至輸出層得到輸出向量。第二個階段為誤差的反向傳播，用期望值與輸出值定義誤差性能函數，從輸出層向前一層逐層計算每個權值矩陣對誤差性能函數的梯度，運用最速下降法更新各層權值矩陣。BP 神經網絡的前向傳播和誤差反向傳播循環往復，最小優化函數收斂時結束。

2.3 基于BP 神經網絡的PID 控制

2.3.1 BP-PID 控制原理

PID 控制要達到理想的控制效果需要不斷地調試kp、ki、kd3 個參數，該組合過程是非線性的，十分繁瑣復雜，并且準確性低。而通過BP 神經網絡的自適應學習過程，不斷地更新權值矩陣，可以更快更好地逼近非線性函數曲面的最小值，調整出最適合當前系統運行狀態的PID 參數。

控制器由兩部分組成：第一部分為PID 控制器，它的kp、ki、kd參數直接由BP 神經網絡實時調整，并對被控對象進行閉環控制。第二部分為BP 神經網絡，它能夠根據誤差性能函數，輸出最佳的kp、ki、kd。BP 神經網絡結合PID 控制的結構框圖見圖6。

圖6 BP 神經網絡結合PID 控制的結構框圖Fig.6 Block diagram of BP neural network combined with PID control

經典增量式數字PID 的控制算式如式（3）所示：

當kp、ki、kd參數可以在線調整時，可將式（3）寫為如式（4）所示：

式（4）為非線性函數，可以通過BP 神經網絡得到最佳控制規律。

2.3.2 BP-PID 的前向傳播

參照圖5，設置一個BP 神經網絡，其結構為3 層，有n個輸入元素，s個隱含層神經元，3 個輸出元素，其中W(2)為第一層的權值矩陣，W(3)為第二層的權值矩陣，f(2)(?)為隱含層的激活函數，f(3)(?)為輸出層的激活函數。輸入向量I的元素對應系統不同時刻的輸入量、輸出量、偏差量等，輸出向量Y的元素分別對應PID 控制器的3 個參數kp、ki、kd。

BP 神經網絡的輸入層輸出如式（5）所示：

式（5）中，i=1, 2, …,n為輸入向量I的第i個元素。隱含層激活函數f(2)(?)的輸入如式（6）所示：

式中：j=1, 2, …,s；為當前隱含層第j個神經元的輸入，為輸入層第i個元素到隱含層第j個神經元之間的權值矩陣。

隱含層的輸出如式（7）所示：

選取具有正負對稱性的雙曲正切S 形tanh 函數作為隱含層激活函數，如式（8）所示：

BP神經網絡激活函數f(2)(?)的輸入如式（9）所示：

式中：h=1, 2, 3；為當前輸出層第h個神經元的輸入；為隱含層第j個元素到輸出層第h個神經元之間的權值矩陣。

輸出層的輸出如式（10）所示：

由于kp、ki、kd不能為負，所以輸出層神經元激活函數取非負的Sigmoid 函數，如式（11）所示：

輸出層的輸出對應PID 的3 個參數，如式（12）所示：

2.3.3 BP-PID 的誤差反向傳播

設d(k)為當前期望響應，y(k)為當前輸出，則當前誤差e(k)如式（13）所示：

若輸出與期望存在差異，則定義均方誤差函數E(k)，如式（14）所示：

為了在E(k)最小值時得到權值矩陣的最優值，利用最速下降法搜索誤差曲面，在梯度為0 時搜索到最優值，通過沿曲面的負梯度方向改變權值可達誤差曲面底部。輸出層E(k)的梯度如式（15）所示：

式（15）中的分離項可根據式（14）求值，如式（16）所示：

由式（3）和式（12）可得式（18）：

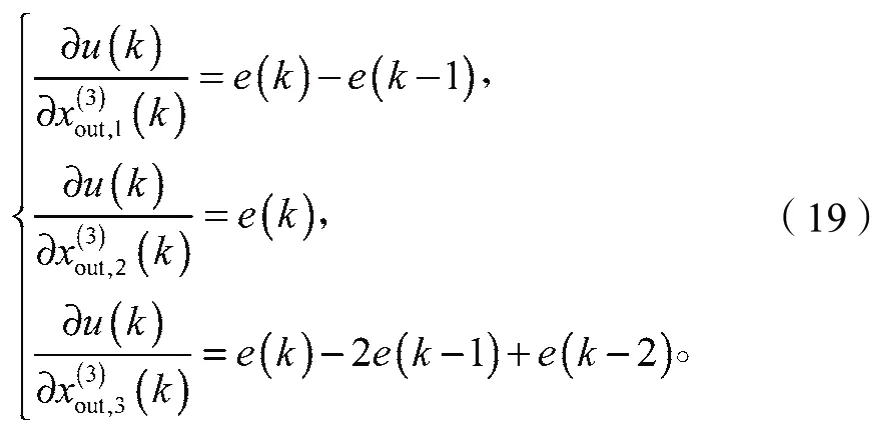
式中：

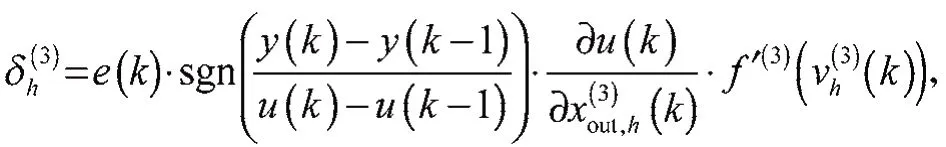
為局部誤差。

運用具有動量更新的反向傳播學習算法，可得輸出層權值更新規則如式（21）所示：

式中：μ為學習率；α為遺忘因子。

隱含層權值的更新規則可由同樣的方法導出，如式（22）所示：

式中：μ>0；0<α<1。

2.3.4 BP-PID 的算法流程

BP 神經網絡結合PID 控制的算法步驟如下：

1）確定BP 神經網絡隱含層層數，設置BP 神經網絡的輸入向量元素個數n、隱含層神經元個數s、各層權值矩陣初值和、學習率μ、遺忘因子α；

2）根據BP 神經網絡的前向傳播算法計算各層神經元的輸入和輸出，輸出層輸出kp、ki、kd參數；

3）根據輸出的kp、ki、kd參數計算PID 控制器的輸出u(k)；

4）根據采樣的d(k) 和y(k) 計算當前誤差e(k)=d(k)-y(k)，并定義誤差性能函數E(k)；

5）根據BP 神經網絡的誤差反向傳播算法，實時更新權值矩陣和；

6）設置k=k+1，回到第二步。

3 仿真測試

為了驗證BP 神經網絡結合PID 控制策略的可行性和有效性，以單相LCL 型并網逆變器為實驗對象，利用Matlab 軟件進行仿真研究。主電路仿真圖如圖7所示。

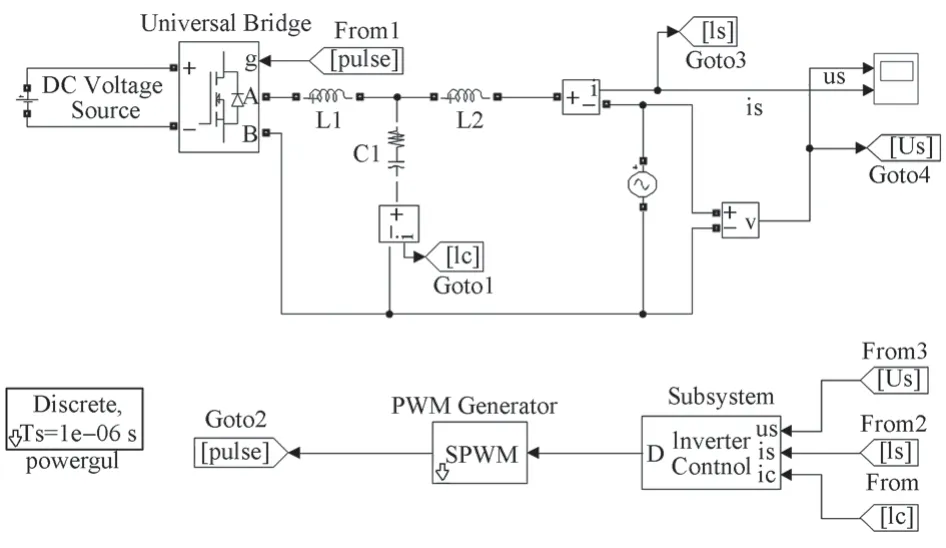
圖7 單相LCL 型并網逆變器主電路仿真圖Fig.7 Main circuit simulation diagram of single-phase LCL grid-connected inverters

圖7中主要器件參數如下：電感L1=3.3×10-3H,電感L2=2×10-3H，電容C1=5×10-6F，開關頻率f=2×104Hz。Control 模塊內部結構如圖8所示。

圖8 逆變器主電路的Inverter Control 模塊內部結構Fig.8 Internal structure of Inverter Control module of the main circuit of inverters

圖中Switch 開關用于選擇使用BP 神經網絡結合PID 控制策略或者使用傳統PID 控制。bppid 模塊內部結構如圖9所示。

圖9 逆變器主電路的bppid 模塊內部結構Fig.9 Internal structure of bppid module of the main circuit of inverters

圖中nn_bppid 模塊是由.m 文件編寫的S 函數，運行BP 結合PID 控制程序，程序中設置學習率μ=0.2，遺忘因子α=0.05。搭建好整體結構模型，將圖8中Switch 開關向上撥動并運行仿真，基于BP 結合PID 控制下的并網電流和電壓波形如圖10 所示。

圖10 基于BP 結合PID 控制下的并網電流和電壓波形Fig.10 Grid-connected current and voltage waveform based on BP combined with PID control

將Switch 開關向下撥動并運行仿真，傳統PID控制下的并網電流和電壓波形如圖11 所示。

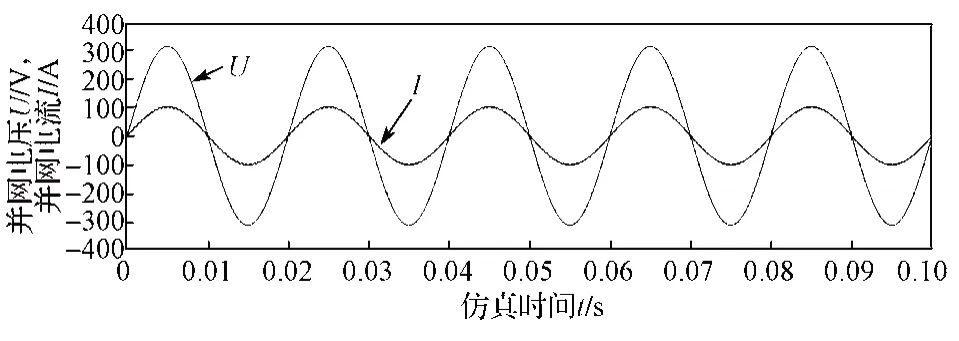
圖11 傳統PID 控制下的并網電流和電壓波形Fig.11 Grid-connected current and voltage waveforms under traditional PID control

通過圖10 與圖11 對比，可發現基于BP 結合PID 控制下的并網電流波形明顯比傳統PID 控制下的并網電流波形的畸變率低，曲線更加平滑。并且在BP 結合PID 控制下的并網電流始終與并網電壓保持同頻率同相位。基于BP 結合PID 控制的nn_bppid模塊輸出的3 個參數kp、ki、kd變化情況如圖12 所示。

圖12 BP 結合PID 控制的可調參數kp、ki、kd 變化情況Fig.12 Changes of adjustable parameters kp、ki、kd of BP combined with PID control

由圖12 可以看出，在運行初期1×10-3s 內，隨著時間推移，kp、ki、kd3 個參數通過誤差反向傳播不斷地調整，以尋找PID 控制的最優效果。從圖8的誤差示波器中可以得到傳統PID 控制下電流跟蹤誤差，如圖13 所示。

圖13 傳統PID 控制下電流跟蹤誤差Fig.13 Current tracking error under traditional PID control

BP 結合PID 控制下電流跟蹤誤差如圖14 所示。

圖14 BP 結合PID 控制下電流跟蹤誤差Fig.14 Current tracking error under BP combined with PID control

對比圖13 與圖14，可發現在傳統PID 控制下，并網電流誤差在0.25 s 內趨于穩定，穩態誤差在±1.0 A 內，并且穩定性較差；而在BP 結合PID 控制下，并網電流誤差在0.18 s 內趨于穩定，穩態誤差在±0.5 A 以內，并且波動幅值較小。上述結果表明：在BP 神經網絡結合PID 控制下的并網電流跟蹤速度快、跟蹤誤差小，可實現并網電流跟蹤。

4 結語

以單相LCL 型逆變器為研究對象，利用BP 神經網絡的自適應學習能力調整PID 控制器的kp、ki、kd3 個參數，提出BP 結合PID 控制的策略，構建BP 結合PID 控制的系統模型。通過仿真表明：在此控制方法下的并網電流跟蹤速度快、跟蹤誤差小，實現并網電流跟蹤。證明了該控制策略的可行性。