基于博弈-灰靶模型的隧道塌方風(fēng)險(xiǎn)評價(jià)*
侯天亮 張義平,2 彭意飛 蔣云萊 黃薇
(1.貴州大學(xué)礦業(yè)學(xué)院,貴州 貴陽 550025;2.貴州一和科技有限公司,貴州 貴陽 550025)
0 引言
當(dāng)前,我國已步入基建工程建設(shè)的高峰期,公路隧道在西部地區(qū)的發(fā)展尤為迅速[1]。至2019年年底,我國公路隧道達(dá)19 067座,同比增長7.5%;隧道總長度達(dá)到1 896.66萬m,同比增長10%[1-2]。隨著隧道建設(shè)跨度和數(shù)量的突破,施工事故頻發(fā)。通過對2005—2019年國內(nèi)109起隧道施工事故進(jìn)行分析可知,塌方、透水突水、爆炸、冒頂事故的占比分別為68.75%、10.4%、93.8%、6.25%[3]。其中,塌方事故占比超過50%。因此,如何科學(xué)合理地確定隧道塌方風(fēng)險(xiǎn)等級已成為隧道施工中的關(guān)鍵問題之一。
近年來,隧道塌方風(fēng)險(xiǎn)評價(jià)模型研究逐步深入,并取得了豐碩成果,為隧道安全施工提供了重要的理論指導(dǎo)。秦勝伍等[4]建立了最大熵-屬性區(qū)別隧道塌方風(fēng)險(xiǎn)評價(jià)模型。呂擎峰等[5]提出并驗(yàn)證了模糊層次-后果當(dāng)量隧道塌方風(fēng)險(xiǎn)評價(jià)模型。Wang等[6]在模糊綜合評判和組合賦權(quán)的基礎(chǔ)上開發(fā)了山嶺隧道塌方風(fēng)險(xiǎn)評價(jià)系統(tǒng)。pǎcková和岳誠東等[7-8]介紹了多種隧道塌方風(fēng)險(xiǎn)評價(jià)模型的特點(diǎn)和案例。翟強(qiáng)等[9]建立了EW-AHP-未確知測度隧道坍塌風(fēng)險(xiǎn)評估模型,并進(jìn)行了驗(yàn)證。但是,目前國內(nèi)可靠性高的隧道塌方風(fēng)險(xiǎn)評價(jià)模型較少,主要是由于評價(jià)指標(biāo)選取及權(quán)重確定不夠客觀、全面,且隧道塌方不確定性因素較多。因此,急需建立一種科學(xué)合理、客觀直接的隧道塌方風(fēng)險(xiǎn)評價(jià)模型解決上述問題。
本文將灰靶理論引入隧道塌方風(fēng)險(xiǎn)評價(jià),提出了博弈-灰靶多指標(biāo)評價(jià)模型。運(yùn)用博弈論對序關(guān)系分析法(G1法)、變異系數(shù)法和熵權(quán)法的權(quán)重進(jìn)行組合優(yōu)化,一方面,能夠減少原始數(shù)據(jù)信息的丟失;另一方面,能夠削弱人為主觀因素和單一權(quán)重帶來的誤差,并通過臨界靶心距的計(jì)算定量確定塌方風(fēng)險(xiǎn)等級的集合,使評價(jià)結(jié)果更加科學(xué)準(zhǔn)確。同時(shí),為了進(jìn)一步確定評價(jià)對象的危險(xiǎn)程度,引入了“靶數(shù)”概念,提高了評價(jià)結(jié)果的可信度和直觀性。實(shí)踐證明,該模型的評價(jià)結(jié)果較為真實(shí),可為隧道塌方預(yù)防提供理論參考。
1 構(gòu)建博弈-灰靶多指標(biāo)評價(jià)模型
1.1 博弈-灰靶多指標(biāo)評價(jià)模型原理與算法
灰靶理論可保證多指標(biāo)決策的客觀性,減少原始數(shù)據(jù)信息的丟失,應(yīng)用較為廣泛。灰靶理論的基本思想為:在既有序列組中,將最優(yōu)序列作為靶心,將其他序列和靶心比較構(gòu)建灰靶模型,進(jìn)而判斷待評對象接近靶心的程度,最終確定風(fēng)險(xiǎn)等級。該模型應(yīng)用性強(qiáng)、簡單高效,可以很好地解決多指標(biāo)決策不確定性問題[10]。考慮到單一灰靶理論精度不高的缺陷,本文運(yùn)用博弈論,對序關(guān)系分析法(G1法)、變異系數(shù)法和熵權(quán)法進(jìn)行組合優(yōu)化,得到最優(yōu)權(quán)重集,結(jié)合灰靶決策理論,提出了基于博弈-灰靶的多指標(biāo)風(fēng)險(xiǎn)評價(jià)模型。博弈-灰靶多指標(biāo)評價(jià)模型構(gòu)建思路與算法流程如圖1所示。
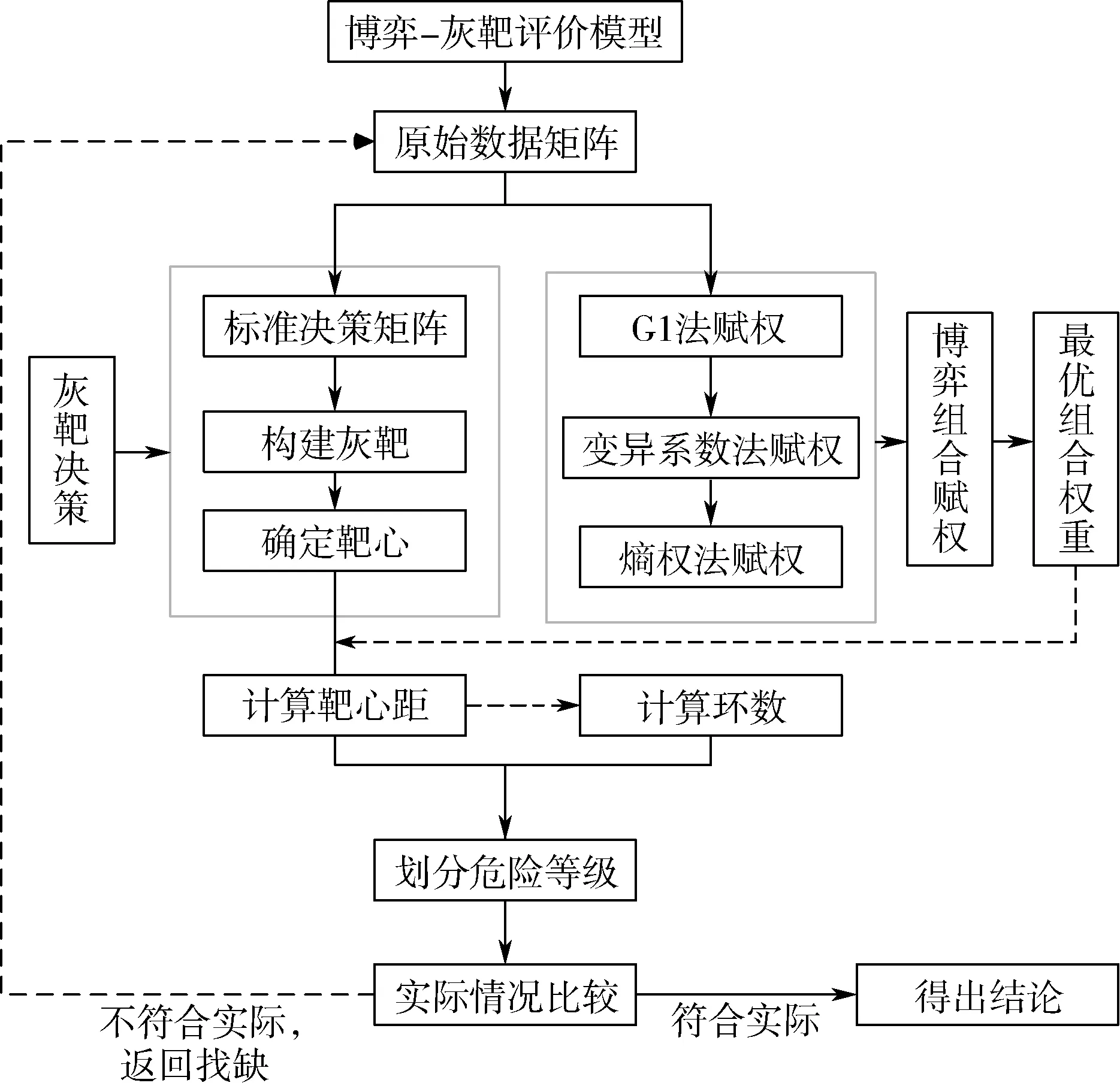
圖1 博弈-灰靶多指標(biāo)評價(jià)模型構(gòu)建思路與算法流程
1.2 構(gòu)建樣本矩陣與決策矩陣
(1)建立樣本矩陣。假設(shè)有m個(gè)評價(jià)對象、n個(gè)評價(jià)指標(biāo),用Cij表示第i個(gè)對象中的第j個(gè)指標(biāo)的信息(1≤i≤m,1≤j≤n)。根據(jù)工程實(shí)際情況,設(shè)定參考序列(靶心)S0=(C01,C02,…,C0n)。
(2)構(gòu)建決策矩陣。為避免量綱差異造成的評價(jià)指標(biāo)權(quán)重偏移問題,通過[-1,1]變換算子對原始數(shù)據(jù)樣本進(jìn)行標(biāo)準(zhǔn)化處理,得到標(biāo)準(zhǔn)化矩陣,即
S={rij}(i=1,2,…,m;j=1,2,…,n)
(1)
(3)計(jì)算原始數(shù)據(jù)標(biāo)準(zhǔn)化后的值。得到:
1)效益性指標(biāo)。公式為

(2)
2)成本型指標(biāo)。公式為
(3)
1.3 計(jì)算靶心距及靶數(shù)
(1)計(jì)算靶心距。考慮到臨界值在風(fēng)險(xiǎn)評價(jià)中的重要性,選取塌方臨界值作為靶心[11]。得到
di=|Si-S0|=
(4)
式中,ω為基于博弈論得到的最優(yōu)權(quán)重集。
(2)計(jì)算靶數(shù)。為使評價(jià)對象風(fēng)險(xiǎn)可視化,將整個(gè)灰靶劃分為0~10環(huán),離靶心越近,環(huán)數(shù)越大,其塌方危險(xiǎn)性越高。即
(5)
式中,D為靶心距矩陣;i=1,2,…,m。
1.4 劃分靶心距的風(fēng)險(xiǎn)等級
從靶心距的定義可知,靶心距di可以反映Si的危險(xiǎn)程度。設(shè)樣本中共有q個(gè)風(fēng)險(xiǎn)等級,令靶心距D=(d1,d2,…,dm),令集合D根據(jù)q個(gè)風(fēng)險(xiǎn)等級的排序?yàn)锽=(B1,B2,…,Bq),令k為正整數(shù)且1≤k≤q,那么第k類臨界值ck=min{Bk},dk=max{Bk},存在:hk=ξdk+1+(1-ξ)ck。其中,ξ∈(0,1),h0=+∞,hq=-∞,進(jìn)而得到q組風(fēng)險(xiǎn)等級的靶心距集合[12]。即
Dq={|d|ho>d1>h1,…,hq-1>dq>hq}
(6)
2 博弈論確定評價(jià)指標(biāo)權(quán)重
2.1 確定單一指標(biāo)權(quán)重
2.1.1 序關(guān)系分析法(G1法)
序關(guān)系分析法是一種主觀賦權(quán)法,與AHP相比,其計(jì)算量較少且無須進(jìn)行一致性檢驗(yàn)。具體計(jì)算步驟如下:
(1)確定序關(guān)系。對n個(gè)評價(jià)指標(biāo)按照重要性進(jìn)行排序。
(2)判斷相鄰指標(biāo)的重要程度。將專家組關(guān)于底層指標(biāo)Ck和Ck-1的重要性之比的理性賦值定義為Bk。得到
(7)
(3)確定權(quán)重ωn。得到
(8)
ωk-1=Bkωk
(9)
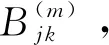
(10)
由此,可得出單指標(biāo)綜合權(quán)重為
(11)
(12)
2.1.2 變異系數(shù)法(標(biāo)準(zhǔn)差率)
變異系數(shù)法是一種客觀賦權(quán)法,計(jì)算量較少且可以有效消除平均數(shù)大小的影響。具體算法過程如下:
(1)計(jì)算各指標(biāo)變異系數(shù),得到
(13)
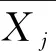
(2)計(jì)算權(quán)重。得到
(14)
2.1.3 熵權(quán)法
熵權(quán)法是一種客觀賦權(quán)法,其基本思想是在綜合考慮各評價(jià)指標(biāo)所含有信息的基礎(chǔ)上,求取一個(gè)綜合權(quán)重向量集[14]。具體計(jì)算步驟在此不做詳細(xì)闡述。
2.2 博弈論組合賦權(quán)
評價(jià)指標(biāo)權(quán)重的確定是通過決策者對主觀因素和客觀因素的綜合考慮,反映評價(jià)結(jié)果的重要程度。采用博弈論組合賦權(quán),將多種確定權(quán)重的方法進(jìn)行組合優(yōu)化,一方面,可以減少單一賦權(quán)造成的信息損失;另一方面,能夠綜合專家組的主觀能動(dòng)性,得到更為客觀全面的指標(biāo)權(quán)重[15]。
假設(shè)運(yùn)用p種算法對同一指標(biāo)集賦權(quán)(當(dāng)p>2時(shí),博弈結(jié)果較優(yōu)),每種算法的權(quán)重向量可表示為ω(i)=[ωi1,ωi2,…ωin](i=1,2,…,p),將該p組向量進(jìn)行隨機(jī)線性組合。得到
(15)
式中,αi為最優(yōu)權(quán)重系數(shù)且αi>0;WT為最優(yōu)權(quán)重向量集。得到
(16)
通過式(16)得到最優(yōu)權(quán)重系數(shù)集α(n)=(α1,α1,…,αi)(n=1,2,…,i)。將其進(jìn)行歸一化處理后,通過式(15)確定博弈組合賦權(quán)的最優(yōu)權(quán)重向量集。
3 實(shí)例分析
以桃子?jì)I隧道進(jìn)口端(T1)和出口端(T2)、白鶴隧道進(jìn)口端(B1)和出口端(B2)的隧道資料、風(fēng)險(xiǎn)特征作為樣本數(shù)據(jù),利用博弈-灰靶多屬性決策模型對隧道塌方危險(xiǎn)性進(jìn)行定量評價(jià)。
3.1 評價(jià)指標(biāo)的選取
隧道塌方評價(jià)指標(biāo)的選取直接影響最終風(fēng)險(xiǎn)等級的客觀性和準(zhǔn)確性。根據(jù)朱捷等[16]對381個(gè)隧道塌方案例的統(tǒng)計(jì)分析可知,主要風(fēng)險(xiǎn)致因占比如圖2所示。此外,結(jié)合國內(nèi)外相關(guān)文獻(xiàn)、隧道的地質(zhì)條件和風(fēng)險(xiǎn)特征選取4個(gè)二級指標(biāo)和12個(gè)三級指標(biāo),其中包含6項(xiàng)定量指標(biāo)(來源于工程實(shí)際資料數(shù)據(jù))和6項(xiàng)定性指標(biāo)(由專家打分得到),并由此構(gòu)建隧道塌方風(fēng)險(xiǎn)評價(jià)指標(biāo)體系,如圖3所示。原始數(shù)據(jù)樣本見表1。
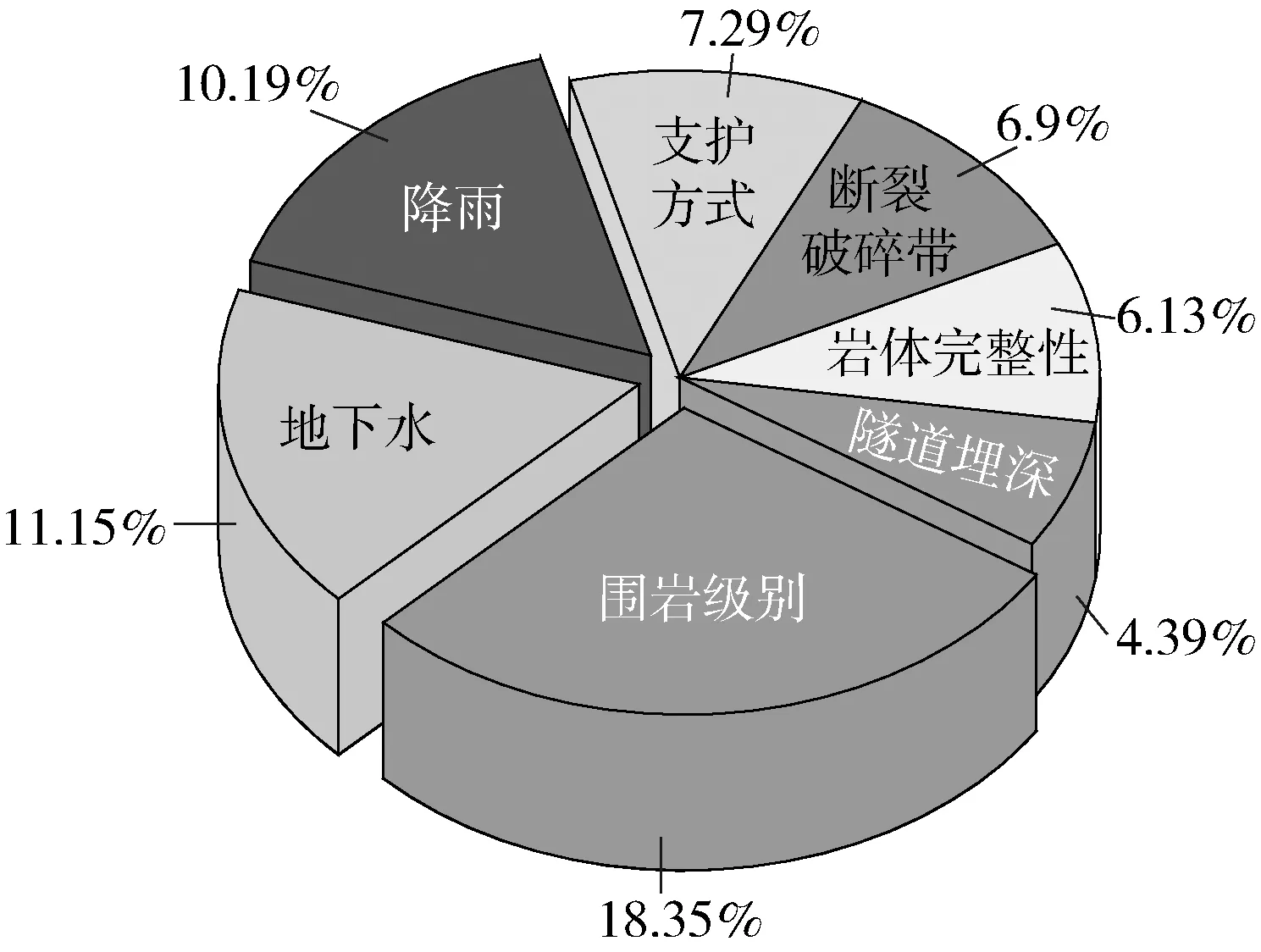
圖2 公路隧道塌方主要風(fēng)險(xiǎn)因素占比
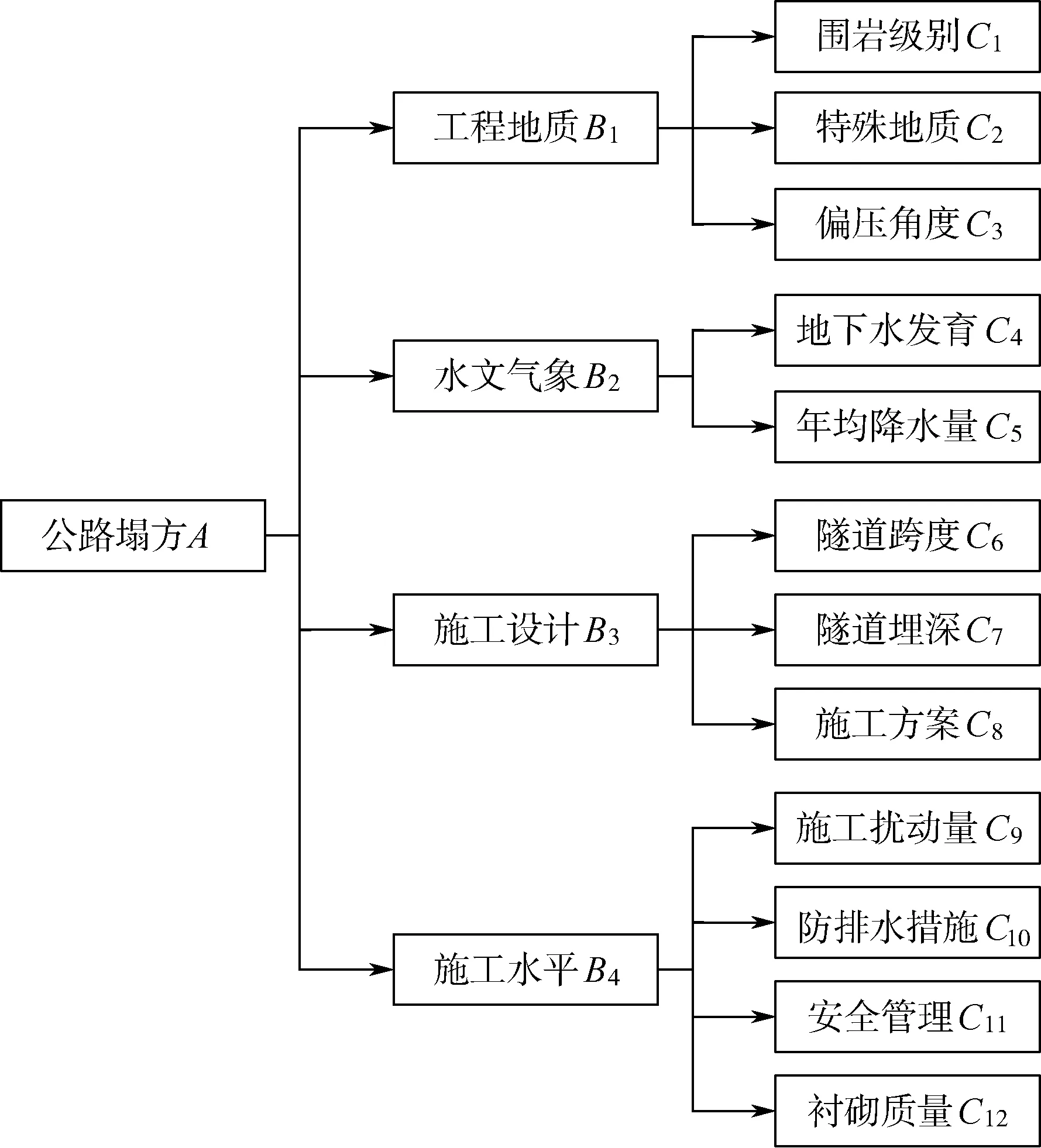
圖3 隧道塌方風(fēng)險(xiǎn)評價(jià)指標(biāo)
3.2 確定隧道塌方指標(biāo)權(quán)重
3.2.1 確定主觀權(quán)重
利用G1法計(jì)算主觀權(quán)重時(shí),為保證評價(jià)結(jié)果的準(zhǔn)確性,共邀請5名專家對各評價(jià)指標(biāo)進(jìn)行排序和打分,根據(jù)式(7)得到各評價(jià)指標(biāo)重要性賦值,根據(jù)式(8)~式(12)得到綜合權(quán)重,見表2。

表2 各評價(jià)指標(biāo)主觀權(quán)重
3.2.2 確定客觀權(quán)重
根據(jù)表1數(shù)據(jù),利用變異系數(shù)法和熵權(quán)法求解客觀權(quán)重。利用式(13)~式(14)得到變異系數(shù)賦權(quán)。同時(shí),利用熵權(quán)法算法確定熵權(quán)賦權(quán)。
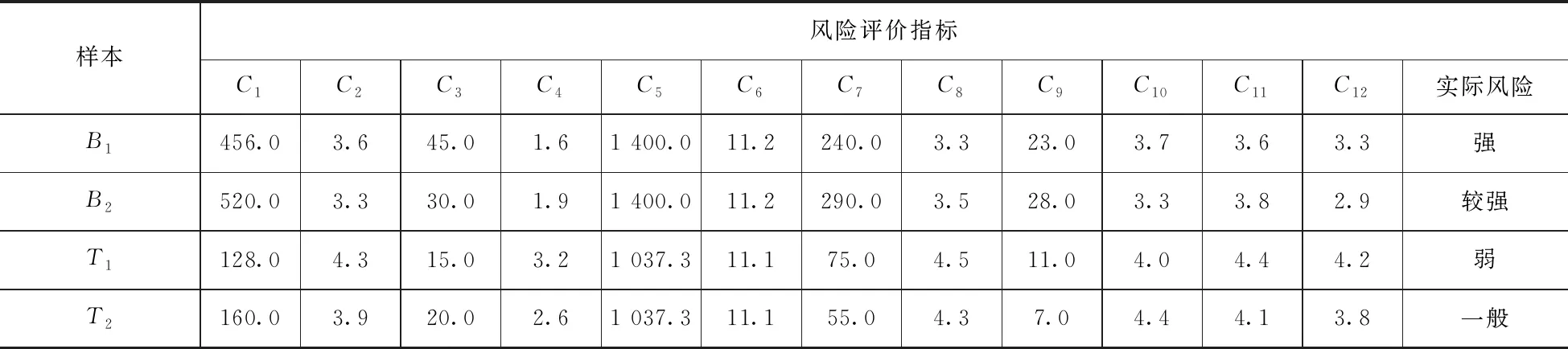
表1 各隧道評價(jià)指標(biāo)原始數(shù)據(jù)樣本
3.2.3 確定最優(yōu)權(quán)重
由式(15)~式(16)計(jì)算得到各賦權(quán)法最優(yōu)權(quán)重系數(shù)(0.317,0.653,0.030),進(jìn)而計(jì)算得到最優(yōu)組合權(quán)重
3.2.4 單一權(quán)重與組合權(quán)重對比
邀請5名專家根據(jù)隧道資料對各指標(biāo)單一權(quán)重和組合權(quán)重與工程的實(shí)際相符程度進(jìn)行打分(滿分為5分),最后取每個(gè)指標(biāo)得分的平均值進(jìn)行判定。各賦權(quán)方法權(quán)重表見表3。由此,繪制多指標(biāo)多算法權(quán)重可視化圖如圖4所示。
從圖4和表3可以看出,各評價(jià)指標(biāo)因?yàn)樗惴ǖ牟煌錂?quán)重大小差異較大。這說明單一權(quán)重的計(jì)算可能會造成原始信息丟失,算法不同引起的偏差對最終評價(jià)結(jié)果且有顯著影響。例如,評價(jià)指標(biāo)C6的變化最大,利用熵權(quán)和G1法得到C6的排序位置較為吻合,但是與變異系數(shù)法相差較大,這是因?yàn)樽儺愊禂?shù)的基本思想是同一指標(biāo)差異性越大,其權(quán)重越大。而隧道跨度(C6)是隧道塌方的重要致因,但本次選取的樣本中隧道跨度相差較小,這就導(dǎo)致了變異系數(shù)法算出的權(quán)重偏差較大,影響實(shí)際結(jié)果的判斷。由此說明,通過博弈論對不同算法的權(quán)重進(jìn)行優(yōu)化組合,得到包含信息量最多的權(quán)重集,其結(jié)果更符合實(shí)際情況。

表3 各賦權(quán)方法權(quán)重表
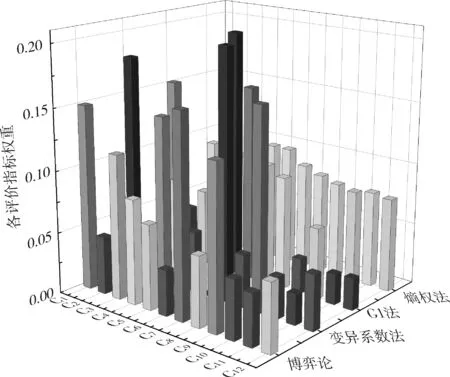
圖4 多指標(biāo)多算法權(quán)重可視化圖
3.3 基于博弈-灰靶的隧道塌方風(fēng)險(xiǎn)計(jì)算
3.3.1 確定標(biāo)準(zhǔn)化決策矩陣
評價(jià)指標(biāo)C3、C5、C6、C9為成本型指標(biāo),其余指標(biāo)均為效益性指標(biāo),根據(jù)式(1)~式(3)得到標(biāo)準(zhǔn)化決策矩陣S,見表4。
3.3.2 確定靶心距和靶數(shù)
根據(jù)博弈論確定的最優(yōu)權(quán)重,由式(4)~式(5)得到靶心距(1.451,1.540,1.831,1.700)和靶數(shù)(10.0,7.7,0.0,3.4)。
3.3.3 確定塌方風(fēng)險(xiǎn)等級
由式(6)得到隧道塌方風(fēng)險(xiǎn)靶心距臨界值和根據(jù)靶心距臨界值確定的風(fēng)險(xiǎn)等級。靶心距臨界值見表5、隧道塌方風(fēng)險(xiǎn)等級見表6。
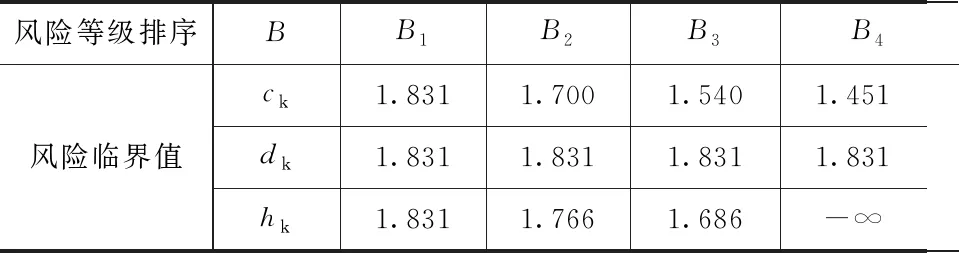
表5 靶心距臨界值
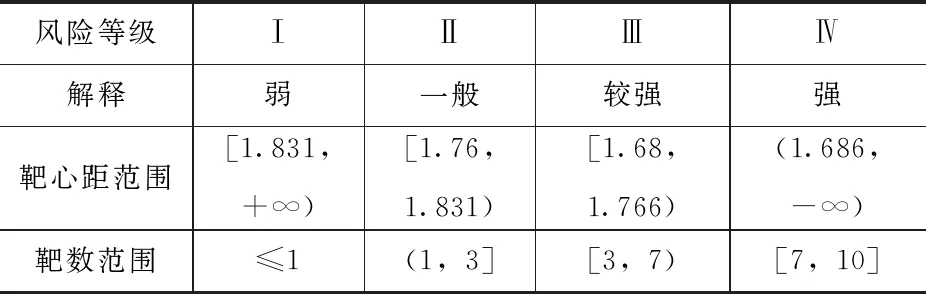
表6 隧道塌方風(fēng)險(xiǎn)等級
3.3.4 各隧道塌方風(fēng)險(xiǎn)評價(jià)
根據(jù)表4和表5,確定各隧道塌方風(fēng)險(xiǎn)等級,即隧道B1、B2、T1、T2的塌方風(fēng)險(xiǎn)等級分別為Ⅳ、Ⅳ、Ⅰ、Ⅲ。同時(shí),為進(jìn)一步直觀描述各隧道的危險(xiǎn)程度,將各樣本的靶心距投影到同一同心圓中(圖5),B1正中靶心,塌方風(fēng)險(xiǎn)性最強(qiáng);B2位于內(nèi)環(huán),塌方風(fēng)險(xiǎn)性較強(qiáng);T2位于外環(huán),塌方風(fēng)險(xiǎn)性一般;T1遠(yuǎn)離靶心,塌方風(fēng)險(xiǎn)性最弱,均與實(shí)際情況接近。這說明本文提出的模型具有可行性和可信度,可為同一隧道不同施工段提供優(yōu)先支護(hù)順序,提高施工安全性。
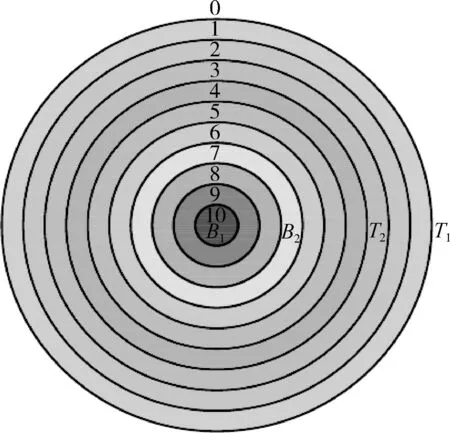
圖5 靶心距投影示意圖

表4 標(biāo)準(zhǔn)化矩陣S
綜上所述,運(yùn)用本文建立的博弈-灰靶評價(jià)模型對4個(gè)隧道進(jìn)行風(fēng)險(xiǎn)性評價(jià),并與實(shí)際風(fēng)險(xiǎn)情況和其他模型的算法進(jìn)行比較,發(fā)現(xiàn)評價(jià)結(jié)果除B2稍有誤差(略高于實(shí)際風(fēng)險(xiǎn),但并不影響評價(jià)結(jié)果),其他均與實(shí)際情況一致,其結(jié)果較其他模型更加全面客觀。各隧道塌方風(fēng)險(xiǎn)等級見表7。
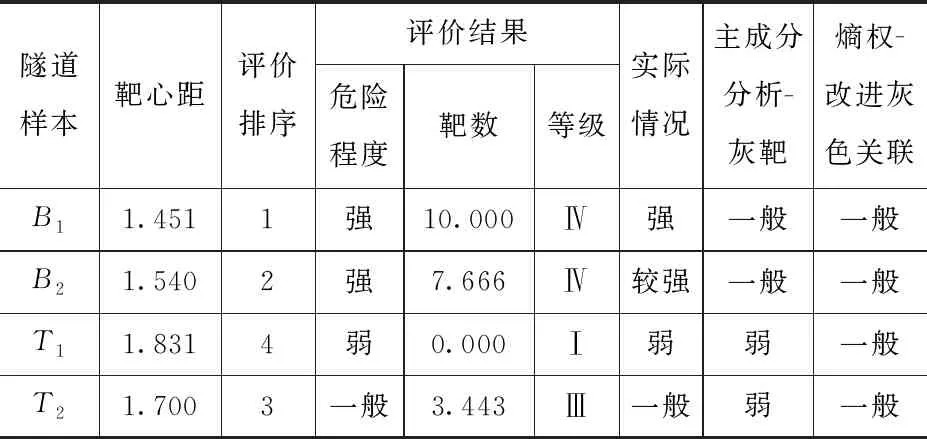
表7 各隧道塌方風(fēng)險(xiǎn)等級
4 結(jié)語
為了對隧道塌方風(fēng)險(xiǎn)進(jìn)行合理準(zhǔn)確的評價(jià),本文建立了博弈-灰靶多指標(biāo)評價(jià)模型。通過資料收集、指標(biāo)選取、多方法結(jié)合演算、現(xiàn)場驗(yàn)證等方法,得出如下結(jié)論:
(1)運(yùn)用博弈論對序關(guān)系分析法(G1法)、變異系數(shù)法和熵權(quán)法確定的權(quán)重進(jìn)行組合優(yōu)化,降低了不同算法帶來的偏差、減少了原始數(shù)據(jù)攜帶信息的丟失,獲得含有原始數(shù)據(jù)信息量最多的最優(yōu)權(quán)重集,使得評價(jià)結(jié)果更加客觀、更具有代表性。
(2)通過靶心距臨界值方程,推導(dǎo)出各等級下靶心距的臨界值,將隧道塌方等級的劃分由定性變?yōu)槎浚瑸楸疚脑u價(jià)模型提供更客觀準(zhǔn)確的風(fēng)險(xiǎn)等級評價(jià)標(biāo)準(zhǔn),使評價(jià)結(jié)果更加科學(xué)準(zhǔn)確。
(3)為進(jìn)一步直觀描述各隧道的危險(xiǎn)程度,引入了“靶數(shù)”的概念。將各樣本的靶心距投影到同一同心圓中,直觀且準(zhǔn)確地顯示了各隧道的塌方危險(xiǎn)程度,且結(jié)論基本與實(shí)際情況一致。
(4)運(yùn)用本文構(gòu)建的博弈-灰靶多指標(biāo)風(fēng)險(xiǎn)評價(jià)模型,確定了各隧道塌方風(fēng)險(xiǎn)等級:白鶴隧道進(jìn)出口端、桃子?jì)I隧道進(jìn)出口端隧道塌方風(fēng)險(xiǎn)等級分別為Ⅳ、Ⅳ、Ⅰ、Ⅲ。將該模型評價(jià)結(jié)果與實(shí)際情況和其他模型進(jìn)行對比,結(jié)果表明該模型評價(jià)結(jié)果與工程實(shí)際最為接近,證明了該模型的準(zhǔn)確性和可行性。

