考慮輸入飽和的直升機機動飛行LPV控制

李 碩, 張紹杰,*, 嚴 鵬, 張 涵, 魯 可,2

(1. 南京航空航天大學自動化學院, 江蘇 南京 211106; 2. 中國直升機設計研究所直升機旋翼動力學重點實驗室, 江西 景德鎮 333001)

0 引 言

直升機機動飛行是指直升機在作戰飛行時靈活改變直升機的速度、方向、高度、姿態的動作,使其完成一系列從有限機動性到迅猛機動性的全部飛行科目。ADS-33E-PRF是一種以任務為導向的直升機駕駛品質規范,一共給出了23種機動飛行科目,并為所有的科目都合理規劃了需要滿足的性能指標要求。為了對機動飛行進行模擬仿真,需要用數學描述的方法界定飛行軌跡的邊界條件,生成可供仿真的導航模型。其中,在不考慮駕駛員建模的情況下,逆仿真方法是直升機機動飛行數值模擬的主要手段。其本質是根據駕駛品質規范劃定的飛行軌跡要求,在直升機運動學方程中附加邊界條件約束,使得求解方程時具有唯一解。

輸入飽和在直升機機動飛行的控制系統中是一個不可忽視的問題。當直升機的姿態或速度的指令信號輸入值較大時,容易超出執行器的作用范圍,導致控制器輸出與執行器輸出不一致,從而引發系統性能下降甚至出現發散的問題。文獻[9]中,在執行機構飽和約束下,針對直升機這種開環不穩定系統,提出了一種兩步法抗飽和控制方法。文獻[10]中,針對超空泡航行體在運動過程中面臨的執行器飽和問題,通過Lyapunov方法,基于多面體理論和線性矩陣不等式的約束,設計了一種狀態反饋控制器。文獻[11]針對三自由度直升機,提出了一種基于混合性能和線性二次調節器的魯棒控制器,將控制輸入間接約束在代價函數中。雖然上述文獻對輸入飽和的研究已有一定的成果,但基于LPV模型對直升機機動飛行的輸入飽和研究較少。

為使直升機機動飛行的輸入出現飽和時仍然能夠跟蹤機動飛行軌跡,本文基于參數依賴的Lyapunov函數和集不變性,提出了一種狀態反饋控制方法。首先在動力學方程的基礎上選用能表征直升機非線性特性的狀態量作為時變參數,采用雅克比線性化方法建立了線性變參數(linear parameter varying, LPV)縱向模型。為了對時變參數進行跟蹤控制,對LPV縱向模型進行了增廣變換。基于吸引域與不變集理論和參數依賴Lyapunov方法,結合參數化線性矩陣不等式(parameterized linear matrix inequalities,PLMI)提出了一種狀態反饋控制器。利用松弛變量技術將難以求解的PLMI條件轉換成易于求解的線性矩陣不等式(linear matrix inequalities,LMI)條件,通過求解LMI得到直升機機動飛行在輸入飽和時保持穩定追蹤的控制律。仿真結果表明閉環系統能夠漸近跟蹤給定指令,且能夠有效地實現抗飽和補償。

1 直升機縱向LPV模型與機動飛行的軌跡描述

1.1 LPV模型

(1)

式中:表示直升機總質量;為直升機沿前向機體軸的線速度;表示沿直升機垂向機體軸的線速度;是俯仰角速率;為俯仰角;慣性矩用來表示;是俯仰力矩;,分別為作用于直升機機體軸和的合力。

常用的建立與非線性模型動態接近的LPV模型的方法有3種:雅克比線性化、狀態變換和函數替換法。由于雅克比線性化法可以在任意平衡點處線性化,易于在非線性模型平衡點處進行線性化處理,因此本文選擇雅克比線性化方法,然后對多個平衡點采用數據擬合法建立LPV模型。

本文參考文獻[22]中建立的LPV模型,選取調度參數,,的高階次冪,即

=[,,,,,,,,,,]

(2)

使用其仿射參數依賴形式的LPV模型:

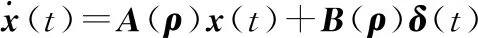
(3)

式中:=[,,,],=[,],為縱向周期變距,為旋翼總距,且

()=+++++++
++++

(4)

()=+++

(5)

式中:(=0,1,…,11),(=0,1,2,3)為適當維數的常數向量。

1.2 機動飛行軌跡描述

懸停科目是ADS-33E-PRF中規定的直升機任務科目基元,該科目考察了直升機從平飛到懸停的能力。基于本文建立的LPV縱向模型,忽略直升機橫側向部分的要求,規定飛行軌跡保持在-平面內,側向速度總為0。

考慮到任務科目的動作要求和性能要求,對直升機機動飛行的軌跡進行數學描述,根據圖1給出的軌跡路線圖和ADS-33E-PRF中給出的期望性能,選擇通用機型在目視良好的狀態下,分時段對直升機的軌跡進行描述。

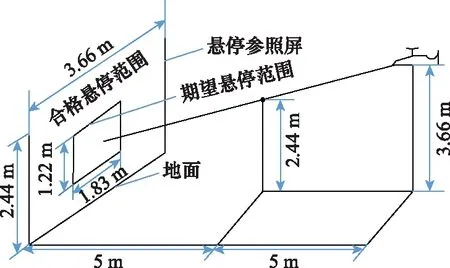
圖1 懸停科目試驗軌跡示意圖Fig.1 Schematic diagram of hovering subject test trajectory

任務科目要求直升機在低于6.096 m的高度下,以3.087～5.144 m/s的地面速度啟動。本文設定直升機以初始高度為3.66 m、初始速度為4 m/s的水平前飛狀態進入該機動。=0 s時刻開始減速下降,產生負的前向加速度,給定地面參照標為2.44 m,減速至=5 s時,懸停在1.22 m處,使得前飛速度=0 m/s,然后保持懸停狀態至時間=35 s。

將直升機的垂向位移用()表示,則-階段,()滿足以下邊界條件:

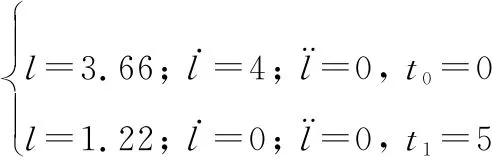
(6)

由邊界條件,可將()表示為5次多項式:

()=+++++

求解可得

()=-0004 7+0058 6-0195 2+366

(7)

將直升機的水平位移用()表示,則-階段,()滿足以下邊界條件:

(8)

同理可解

()=0016-016+4

(9)

1.3 模型的增廣

第12節給出了懸停科目的機動飛行軌跡數學描述,可以看出,懸停科目需要速度分量和速度分量進行跟蹤控制。因此,需要考慮對參考輸入的跟蹤控制問題,記指令信號為()=[,],系統的輸出為

()=+()

(10)

式中:

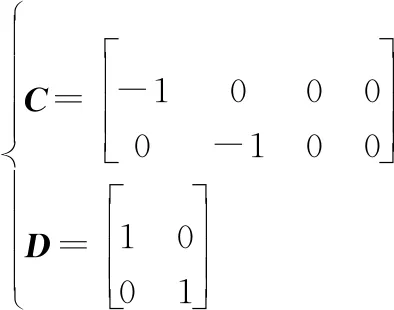
(11)

則系統控制目標為

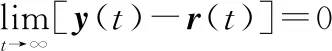
(12)

將跟蹤誤差積分項

(13)

與直升機縱向LPV模型(見式(2))聯合,得出增廣系統:

(14)

2 控制律設計

2.1 PLMI條件

考慮如下具有仿射參數依賴的LPV系統:

(15)

式中:=[,,…,]為可時刻檢測的變參數,且在如下給定范圍變化:

(16)

(17)

()是系統的輸入指令信號;()為性能輸出;()為系統的控制輸入;sat(·)代表控制輸入的飽和函數,定義為

(18)

式中:表示飽和閾值。為方便書寫,將下文中()省去。

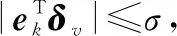
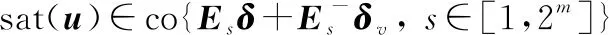
(19)

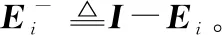
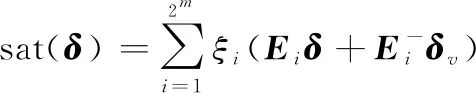
(20)

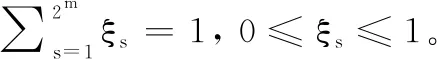
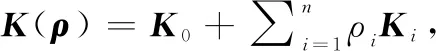
(1) 當控制輸入信號飽和時,對于∈,閉環系統的軌跡必須有界。

(2) 控制性能目標是讓閉環系統增益盡可能小,或使其小于一給定值,即有最小值>0,使得

(21)

定義對稱多面體

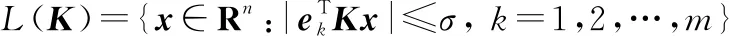
如果對于=1,2,…,,控制輸入均未達到飽和,則∈()。定義()=,>0,若存在正實數,則定義橢球體

(,)={∈:≤}

(22)

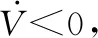
min log(det())

使得

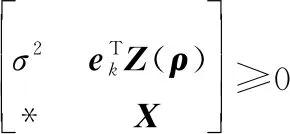
(23)

(24)

式中:

()=()

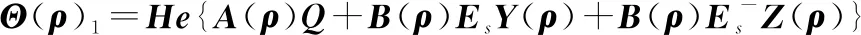
(25)

能夠使閉環系統漸近穩定并具有增益。

選取橢球體(,)上的Lyapanov函數

()=()()

(26)

式中:為常數矩陣。定義橢球體

(,)={∈:≤}

(27)

可將單位橢球體表示為

(28)

式(28)中橢球體是一個正不變集,意味著對任何初始條件,若滿足∈(,),則當≥,()∈(,)。

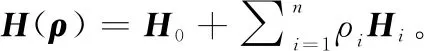
那么

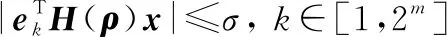
(29)

進一步,對∈[1,2],式(29)可變換為

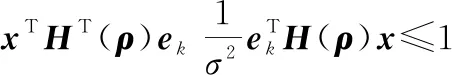
(30)

且有

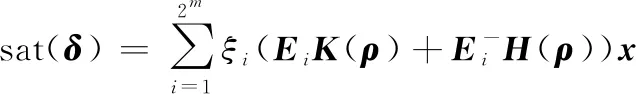
(31)

(32)

由于()定義在橢球體上,有()∈(,),∈()。令

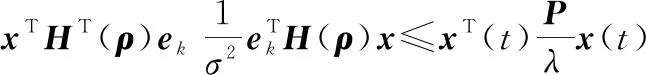
(33)

對不等式變換,兩邊省略。利用Schur補定理,且兩邊同時乘diag[,λ],可得到不等式(23)。接下來對式(24)進行證明。

若有以下不等式:

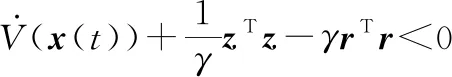
(34)

成立,則設計條件2中的不等式(21)可以被驗證。

進一步,由式(20),式(34)可寫成

(35)

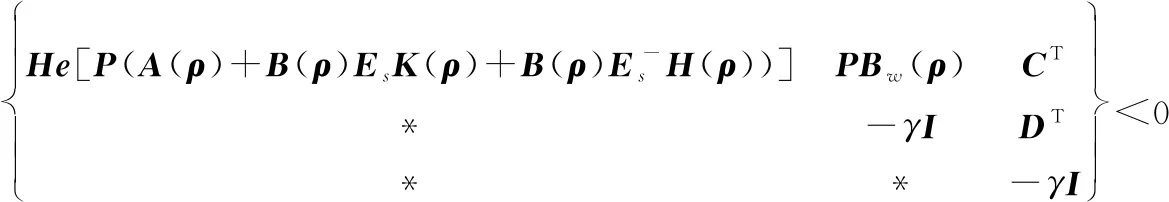
(36)

由于式(36)的形式是雙線性矩陣不等式,因此可以通過前后相乘[,,]進行全等變換,同時整個矩陣乘。得到公式

(37)

令

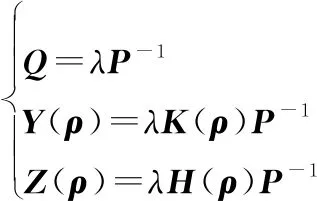
(38)

從而得到式(24)。

通過對橢球體(/λ)，即對()進行最優求解，從而可使系統初始條件的允許范圍最大化。至此定理1證畢,得到控制器設計的PLMI條件。

證畢

2.2 LMI條件

上述PLMI條件涉及無窮多個LMI條件,因此求解控制器的任務是復雜難解的。為了克服這一點,使用松弛變量技術將第2.1節中求出的PLMI條件轉換為時變參數的LMI條件。

基于松弛變量技術,時變參數的約束(16)可以轉變為

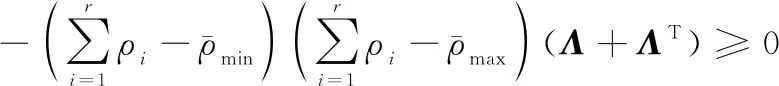
(39)

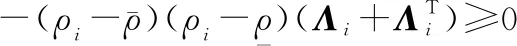
(40)

式中:矩陣∈×,∈×滿足

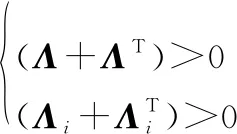
(41)

對于PLMI條件式(23),結合式(39)～式(41),有

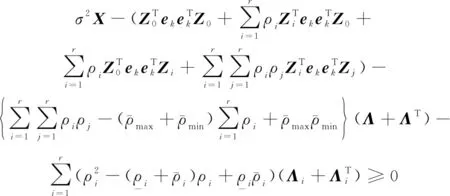
(42)

定義向量()=[,,…,],式(42)可寫為

(43)

式中:

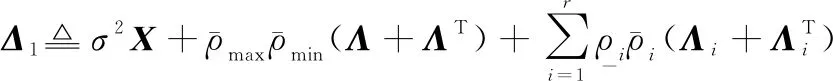
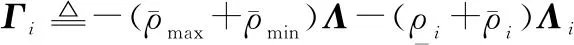
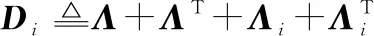
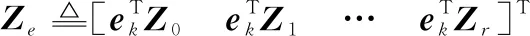
由Schur補定理,式(43)等價于

(44)

同理對于PLMI條件式(24),結合式(39)～式(41),有

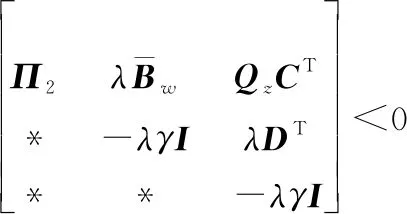
(45)

式中:

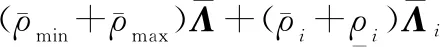
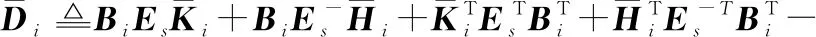
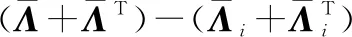
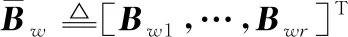
證畢

3 仿真分析

參考文獻[22]中給定的直升機數據,通過定理2中LMI對LPV模型式(10)、式(14)進行輸入飽和的控制律求解。同時給定時變參數的范圍為

(46)

(47)

(48)

仿真得到直升機模型的速度分量和速度分量響應跟蹤曲線如圖2和圖3所示。垂向位移()和前向位移()的響應跟蹤曲線如圖4和圖5所示。從圖2和圖3可以看出,速度分量和速度分量以較快的響應速度跟蹤了參考輸入,即直升機能夠在規定時間范圍內完成平穩的懸停過渡。

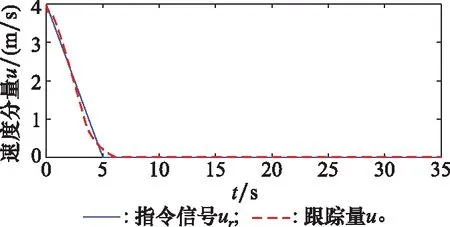
圖2 速度分量u的響應跟蹤曲線Fig.2 Response tracking curve of velocity component u

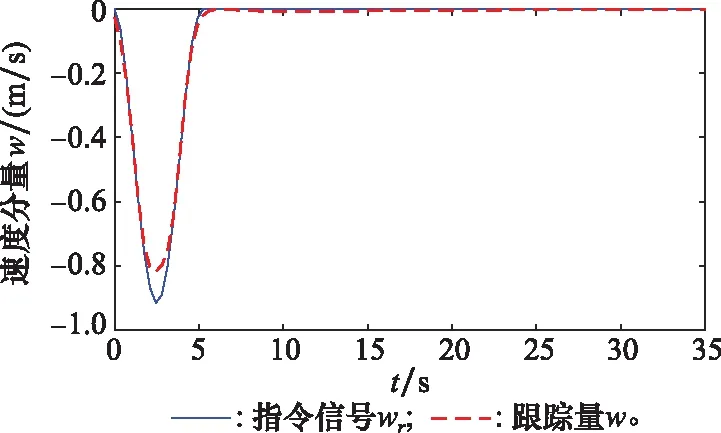
圖3 速度分量w的響應跟蹤曲線Fig.3 Response tracking curve of velocity component w

圖4 垂向位移l的響應跟蹤曲線Fig.4 Response tracking curve of vertical displacement l

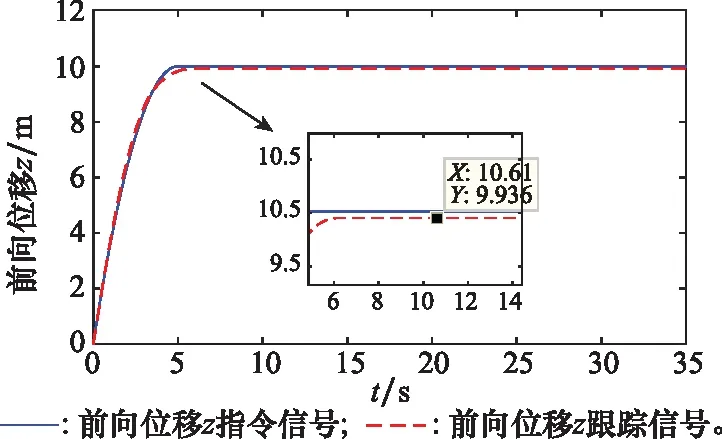
圖5 前向位移z的響應跟蹤曲線Fig.5 Response tracking curve of forward displacement z

ADS-33E-PRF中給出了不同類型的直升機的期望性能與合格性能。對于通用機的要求是高度偏差保持在正負0.61 m內,相對于地面點的縱向偏差保持在0.91 m內。對于本文選取的通用機型,從圖4可以看出,垂向位移偏差為0.23 m,在合理的誤差范圍內,有較為理想的跟蹤效果。表明通用直升機在進行懸停機動時可以保持高度偏差在期望性能范圍內,30 s內也能夠保持穩定懸停,從圖5可以看出,直升機在保持懸停的時間段內,前向位移偏差為0.674 m,能夠保持在0.91 m內,滿足期望性能要求。

考慮輸入飽和時,控制器輸入量的仿真曲線如圖6和圖7所示。從圖中可以看出,所設計的抗飽和控制器在對指令信號進行跟蹤的同時,輸入量可保持在所設定的-0.1～0.1 m范圍內,實現了抗飽和補償。實驗結果表明基于輸入飽和控制器,直升機可以在一定性能范圍內完成懸停科目的試飛。

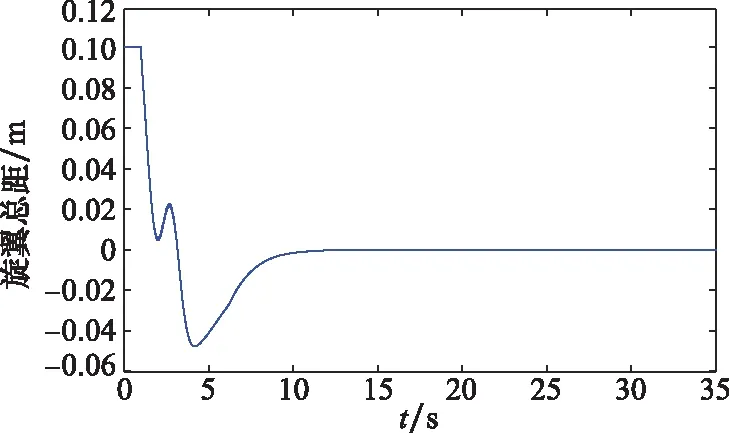
圖6 旋翼總距Fig.6 Collective pitch

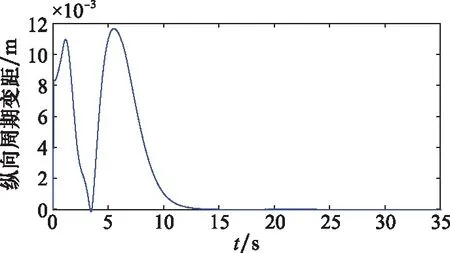
圖7 縱向周期變距Fig.7 Longitudinal cyclic coefficient

4 結 論

本文以直升機為研究對象,針對直升機機動飛行過程中遇到的輸入飽和問題,在動力學方程的基礎上選用能表征直升機非線性特性的狀態量作為時變參數,采用雅克比線性化方法建立了LPV縱向模型。且為對時變參數進行跟蹤控制,對參考文獻[22]提供的模型進行了增廣變換。通過求解定理2中的LMI條件得到了直升機機動飛行在輸入飽和時可保持穩定追蹤的控制律。仿真結果表明閉環系統能夠漸近跟蹤給定指令,且能夠有效地實現抗飽和補償。