新型的基于堆棧式ELM的時變信道預測方法

張 捷, 楊麗花, 聶 倩

(1. 南京郵電大學通信與信息工程學院, 江蘇 南京 210032; 2. 江蘇省無線通信重點實驗室, 江蘇 南京 210003)

0 引 言

高速鐵路(high speed railway, HSR)因其高效安全的特點被廣泛部署,目前針對HSR場景下的無線通信已開展了大量的研究。在HSR場景下,列車時速將超過300 km,如此高的移動速度將會產生嚴重的多普勒頻移,造成信道發生快速隨機變化,使得此場景下的信道獲取更具挑戰性。傳統獲取信道狀態信息(channel state information, CSI)的方法是采用信道估計技術,然而信道估計技術在處理過程中存在一定的時延,通過其獲取的CSI對于快速時變信道而言會出現嚴重的老化現象,此時的CSI已不能準確表征當前信道的真實情況。為了減少信道老化引起的系統性能損失,信道預測技術被提出,其基本的思想是根據歷史時刻的CSI來提前預測未來的信道信息,并且目前針對HSR環境已開展了大量信道預測技術的研究。

傳統的信道預測方法主要是將當前時刻的信道和過去時刻的信道以一種線性組合的方式來預測未來時刻的信道,即線性預測方法,其中最為常用的方法是基于二階自回歸(autoregressive, AR)模型的信道預測方法。線性預測方法在慢時變信道中能夠取得較好的性能,但是在HSR場景下信道的快速時變使得該場景的信道具有很強的非線性特性,在此場景下采用線性預測方法將使得預測性能出現惡化。因此,需要建立非線性預測模型,通過非線性預測來提高信道預測的精度,更好地適應快速時變信道。

目前,常用的非線性信道預測方法主要包括支持向量機(support vector machine, SVM)方法和深度學習方法,其中深度學習方法對于快速時變信道具有較好的預測性能,文獻[13]給出了利用遞歸神經網絡(recurrent neural network, RNN)實現信道預測的方法,文獻[14-16]給出了基于長短期記憶(long short-term memory, LSTM)的信道預測方法,但是這兩類信道預測方法復雜度較高。文獻[17]給出了一種基于反向傳播(back propagation, BP)神經網絡的瑞利衰落信道預測方法,該方法首先構造稀疏信道樣本進行訓練網絡,其次基于早期停止策略來防止訓練過程中出現過擬合現象,因此該方法取得了較好的預測性能。然而,BP算法存在學習速度較慢、泛化能力不強以及局部最優等缺陷。為此,文獻[18]給出了一種基于單隱藏層前饋神經網絡的極限學習機(extreme learning machine, ELM)信道預測方法,該方法首先隨機產生隱藏層權值,且計算得到隱藏層的輸出,然后通過求解最小二乘問題得到網絡的輸出權值,從而獲得最終的預測網絡,該方法不僅學習速度快,而且泛化性能較好。但是ELM作為一種淺層結構,在處理擁有復雜特征的原始數據時存在一定的局限性。文獻[19]給出了一種基于堆疊泛化原理的預測模型,稱為堆棧式ELM方法,該方法結合ELM方法得到的預測結果,對原始輸入樣本進行隨機偏移,然后作用于一個核函數上以實現對偏移后特征矩陣的再次變化,從而得到新的特征,因此該方法是一種深層ELM模型,其能夠從原始輸入中提取有效的深層特征,具有較好的預測性能。然而,文獻[17-19]給出的方法均未充分考慮歷史信道與當前信道之間的變化,在線上預測時均采用固定的網絡模型,這將導致信道預測精度受限。

文獻[20]給出了一種在線序列極限學習機(online sequential ELM, OS-ELM)方法,該方法首先利用ELM方法獲得網絡輸出權值,并利用順序到達的數據采用遞推的方法來對網絡的輸出權值進行更新,該方法在時間序列預測領域具有優越性能。信道預測技術屬于時間序列預測的范疇,因此,若利用OS-ELM方法來實時更新線下訓練時獲取的網絡初始輸出權值,可以充分地利用最新到來的歷史信道信息,更好地適應信道的變化,獲得較好的預測性能。但是,OS-ELM方法采用的是淺層ELM,不能從原始數據中提取有用的更深層特征,為此利用其獲取的信道精度需要提高。

為此,針對HSR環境,本文提出了一種新型基于堆棧式ELM模型的信道預測方法。線下訓練時,新方法利用堆棧式ELM模型從歷史信道中提取有用的深層特征與網絡輸出權值;線上預測時,新方法首先利用新的歷史信道訓練樣本對網絡輸出權值進行更新,然后基于更新后的輸出權值獲取當前時刻的信道信息。研究結果表明,新方法較現有方法能夠取得更高的預測精度,適用于高速移動場景中時變信道的獲取。

1 信號模型

考慮一個單輸入單輸出正交頻分復用(orthogonal frequency division multiplexing, OFDM)系統,假設為頻域第個發送的OFDM符號,且=[(,0),(,1),…,(,-1)],其中(,)為第個OFDM符號上第個載波上的調制后的發送信號,是一個OFDM符號具有的子載波數。信號進行點快速傅里葉逆變換(inverse fast Fourier transform, IFFT)后,則時域發送信號為

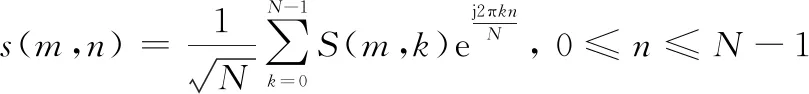
(1)

在HSR環境中,基站普遍建立在鐵軌沿線,這樣的部署方式使得基站與列車之間通信的無線信道中存在一個極其強的直射(line-of-sight, LOS)分量,故在此場景下,采用的信道模型通常是萊斯信道,即

(2)

在接收端,假設理想定時同步,則第個接收到的OFDM符號可以表示為

(3)

2 新型的信道預測方法

新方法包括線下訓練和線上預測兩部分。由于堆棧式ELM是一種深度ELM,其可以從復雜的原始數據中提取深層特征,并且其學習速度快、泛化性能好。因此,新方法在線下訓練中將采用堆棧式ELM從歷史信道信息中獲取信道的深層特征,以提高線上信道預測的精度。下面將對堆棧式ELM及新方法原理進行詳細介紹。

2.1 堆棧式ELM算法

圖1給出了堆棧式ELM的基本原理圖,作為一種堆疊式的模型,堆棧式ELM由多個ELM堆疊而成,在每一個ELM模塊中,首先基于原始特征矩陣,使用ELM方法得到對應輸出,然后基于該輸出對原始特征矩陣做一次隨機偏移,并利用一個核函數生成新的特征矩陣,作為下一個ELM模塊的輸入,以此類推。

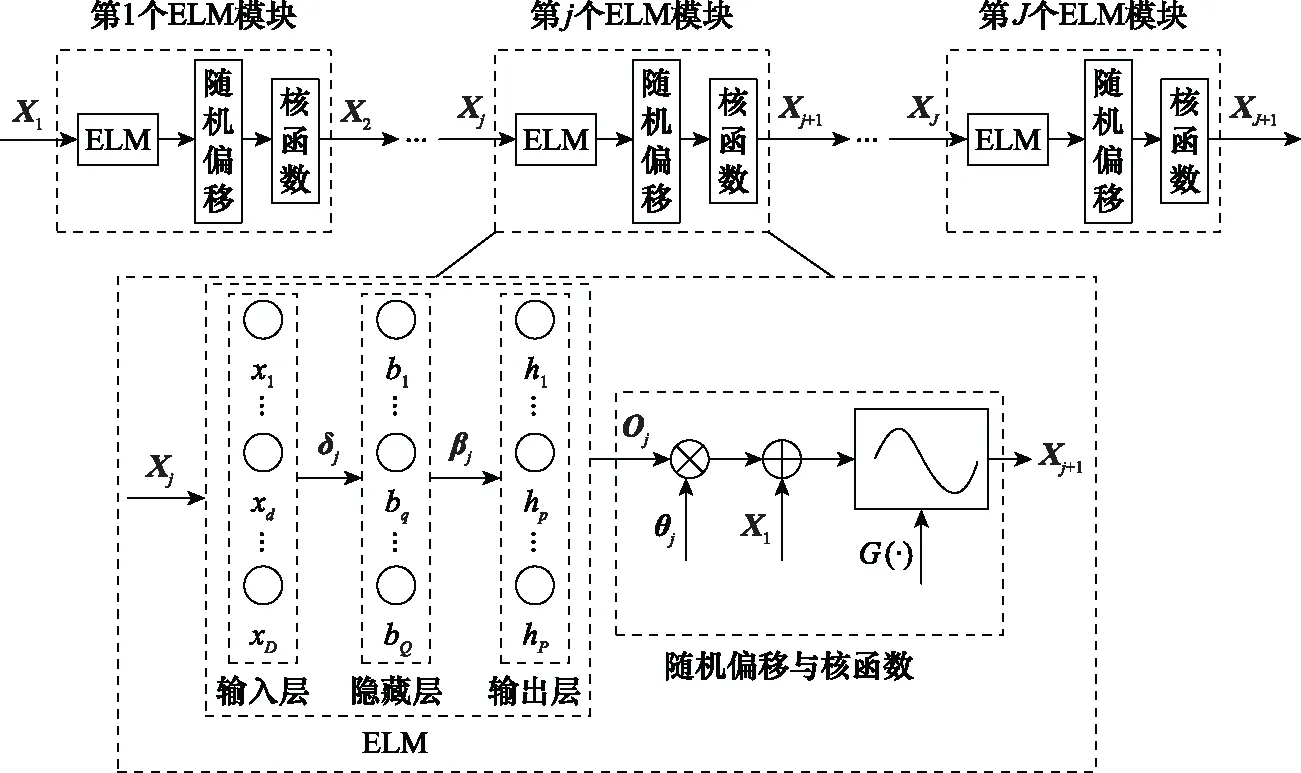
圖1 堆棧式ELM的原理圖Fig.1 Schematic diagram of stacked ELM

ELM基于單隱藏層前饋神經網絡,隨機生成輸入層和隱藏層之間的權值,并利用隱藏層的輸出矩陣與最小二乘方法獲得網絡的輸出權值,即

(4)

(5)

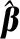
利用式(4)可以得到網絡的輸出為

(6)

由于此時利用式(6)獲得的結果可能并不理想,因此利用該結果對原始特征矩陣進行隨機偏移,然后作用于一個核函數以實現對偏移后特征矩陣的再次變化,則可以獲得新的特征矩陣。為此,獲得的新特征矩陣+1為

+1=(+λ)

(7)

式中:(·)是Sigmoid函數;投影矩陣∈×隨機取樣于正態分布(0,1);是權重參數,用來控制隨機偏移的程度。

2.2 基于堆棧式ELM的時變信道預測方法

新方法基于堆棧式ELM方法挖掘歷史信道的深層特征,獲得網絡初始輸出權值,再利用遞推公式實現輸出權值的更新,從而實現時變信道的預測。新方法主要由線下訓練與線上預測兩部分組成,其中線下訓練階段的主要作用是從歷史信道中提取信道的深層特征,并基于該深層特征,通過求解一個最小二乘問題,獲得網絡的初始輸出權值;在線上預測階段,為了適應信道的變化,首先基于新構造的歷史信道樣本與初始的輸出權值對網絡輸出權值進行更新,并基于更新后的輸出權值獲取當前時刻的信道。

新方法是時域信道預測方法,對于多徑信道而言,需要逐徑進行預測。由于每一徑的信道預測方法是一樣的,因此在下面的論述中將省略信道徑數的標識。

2.2.1 線下訓練階段

在新方法中,線下訓練的主要目的是基于堆棧式ELM方法提取原始輸入樣本的深層特征表示,并利用深層特征與最小二乘方法獲取網絡的初始輸出權值。

假設是由個樣本組成訓練樣本集,其可以表示為

={(,),(,)，…,(,),…,(,)}

(8)

式中:(,)表示為第個訓練樣本,為輸入樣本,為理想信道,其可以表示為

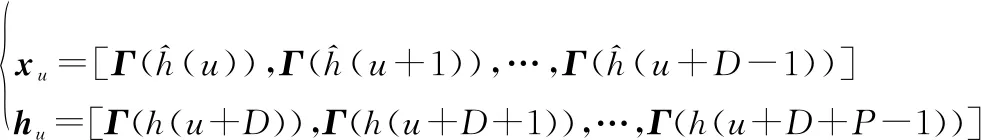
(9)

(())=[Re(()),Im(())]

(10)

式中:Re(·)和Im(·)分別為取實部和虛部操作。

輸入樣本經過深度為的堆棧式ELM方法得到最終的特征矩陣,并利用式(5)得到隱藏層的輸出矩陣,然后根據式(4)得到網絡的初始輸出權值,即

(11)

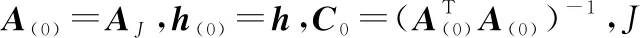
在線下訓練階段,采用堆棧式ELM方法從歷史信道中提取信道的深層特征,能夠有效地處理擁有復雜特征的原始數據,有利于提取出更多有用的信息,基于歷史信道的深層特征矩陣來獲得網絡的初始輸出權值,可以提高預測的準確性。

2.2.2 線上預測

在線上預測階段,基于線下訓練的具有初始輸出權值的網絡,只需輸入前個時刻的歷史信道估計來實時更新網絡的輸出權值,然后基于更新后的輸出權值預測得到當前時刻的信道。

假設線上預測階段網絡輸入樣本為前個時刻的歷史信道信息,基于堆棧式ELM方法可獲得式(7)的特征矩陣,再根據式(5)計算隱藏層的輸出矩陣,然后采用式(12)中的遞推公式對線下訓練后的網絡的輸出權值進行更新處理,從而獲得最終的網絡輸出權重。

(12)

基于更新后的輸出權重,根據網絡輸出權重與輸出之間的關系,可以獲得網絡的輸出為

(13)

式中:為第個ELM模塊中網絡的輸入層與隱藏層之間隨機產生的權值矩陣,且=[,,…,],為第個ELM模塊中隨機生成的隱藏層偏置矩陣；(·)為實數轉復數的運算。

3 性能仿真與復雜度分析

3.1 性能仿真

本節將對新方法進行計算機仿真與分析。仿真中采用的是長度為128的OFDM符號,導頻結構為均勻分布的數目為32的梳狀導頻。車載速度考慮500 km/h,采用5徑的萊斯信道。載波頻率為2.35 GHz和3.5 GHz,子載波間隔為15 kHz。網絡的輸入神經元數目=10,隱藏層神經元數目=10,輸出層神經元=1。仿真中,訓練樣本數為=2 000。為了與新方法性能進行對比,仿真中給出了文獻[18-20]中方法的性能,其中文獻[18]為基于ELM的預測方法,文獻[19]為基于堆棧式ELM的預測方法,文獻[20]為基于OS-ELM的預測方法。

圖2給出了載波頻率為2.35 GHz時新方法與文獻[19]采用不同堆棧ELM深度時的均方誤差(mean square error, MSE)性能曲線。從圖2中可以看出,新方法與文獻[19]的預測性能均會隨著信噪比(signal to noise ratio, SNR)的增加而逐漸提高。在同一方法下,尤其是低SNR時,堆棧深度的增大可以提高預測性能,這是因為隨著堆棧深度的增加,可以更好地從原始數據中提取出更多有用的信道特征。在相同堆棧深度時,新方法的性能要優于文獻[19],這是因為新方法充分利用了新到來的歷史信道數據對預測網絡輸出權值的實時更新,使其更接近預測的信道環境。

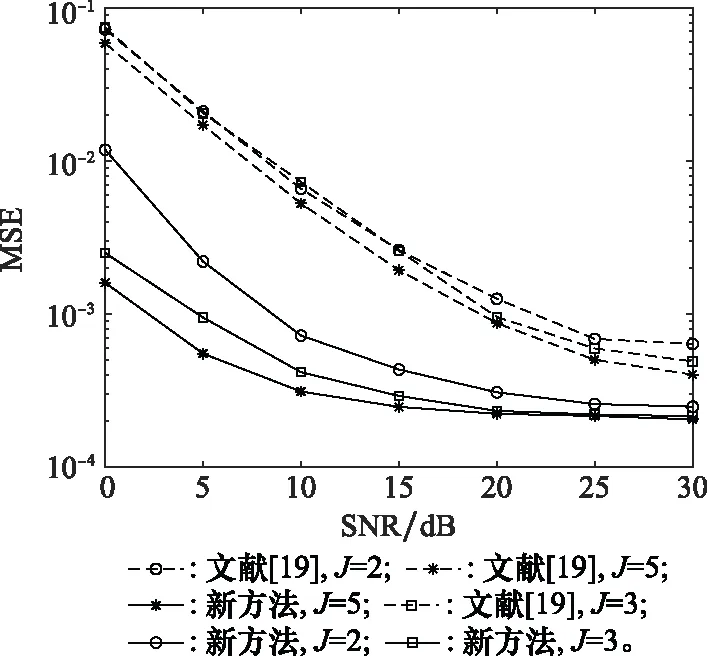
圖2 不同堆棧深度下本文方法與文獻[19]的MSE性能 (fc=2.35 GHz,萊斯因子為5)Fig.2 MSE performance of the proposed method and reference [19] under different stack depths (fc=2.35 GHz, Ricean factor is 5)

圖3給出了載波頻率為3.5 GHz時新方法與文獻[19]采用不同深度的堆棧式ELM方法下的MSE性能。與圖2相比,2種方法的預測精度均會降低,這是由于載波頻率增大會使得對應的多普勒頻移變大,從而使得信道的時變性更強,這將導致信道預測精度的降低但是新方法的性能仍優于文獻[19]。考慮堆棧深度越大,預測方法的計算復雜度將越高,因此,選擇合適的堆棧深度應綜合考慮預測性能與計算復雜度。在后面的仿真中,本文考慮堆棧深度為2。

圖3 不同堆棧深度下本文方法與文獻[19]的MSE性能(fc=3.5 GHz,萊斯因子為5)Fig.3 MSE performance of the proposed method and reference [19] under different stack depths (fc=3.5 GHz, Ricean factor is 5)

圖4給出了新方法采用不同數目的訓練樣本時的MSE性能。仿真中萊斯因子為10,載波頻率3.5 GHz,堆棧深度為2。從圖4可以看出,新方法隨著訓練樣本數的增加,其MSE性能也越來越好,尤其是在低SNR時,由于訓練樣本數越多越有利于數據深層特征的提取。然而,訓練樣本數越多,線下訓練網絡的計算復雜度越高。因此,訓練樣本數的選擇至關重要。

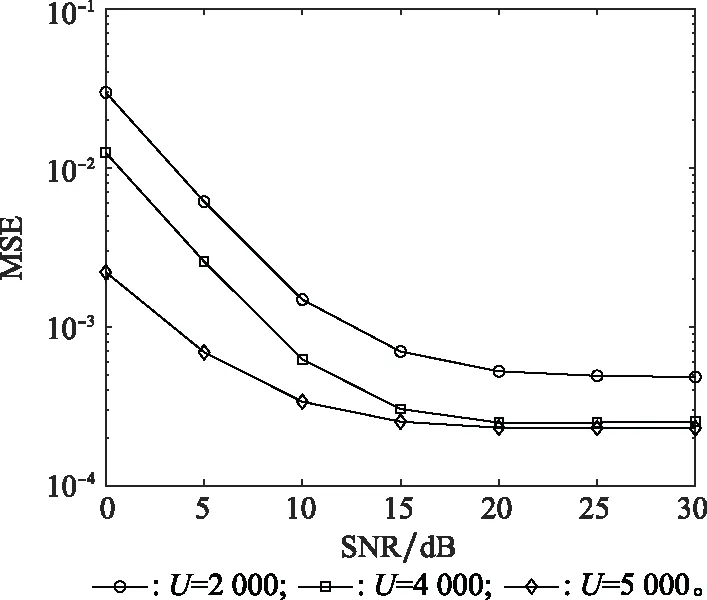
圖4 本文方法采用不同訓練樣本數時的MSE性能(fc=3.5 GHz,萊斯因子為10)Fig.4 MSE performance of the proposed method with different numbers of training samples (fc=3.5 GHz, Ricean factor is 10)

不同信道預測方法的MSE性能比較如圖5所示。仿真中萊斯因子為5,載波頻率3.5 GHz,堆棧深度為2,訓練樣本數為2 000。

圖5 本文方法與現有信道預測方法的MSE性能比較(fc=3.5 GHz,萊斯因子為5)Fig.5 Comparison of MSE performance between the proposed method and existing channel prediction methods (fc=3.5 GHz, Ricean factor is 5)

從圖5可以看出,隨著SNR的增大,各種預測方法的性能均有提高。相比于文獻[18]的預測方法,文獻[19]采用了深層ELM模型,有利于提取復雜的數據特征,因此取得了較好的性能。文獻[20]利用新的歷史信道訓練樣本,采用了遞推算法更新網絡的輸出權值,具有更強的適應性,因此性能得到改善。本文方法由于采用深層ELM模型,利用新到來的歷史信道實時更新預測網絡的輸出權值,不僅可以從原始數據中提取出有用的特征表示,還充分利用歷史信道,實現了預測網絡輸出權重的更新調整,因此新方法具有更好的性能。

3.2 計算復雜度

本節主要對比分析不同信道預測方法的計算復雜度,如表1所示。可以看出,文獻[18]方法具有較低的計算復雜度,但是其MSE性能最差。文獻[19]方法在線下訓練中的復雜度要高于文獻[20],這是因為文獻[19]線下采用的是深層ELM來訓練網絡,增加了復雜度,而在線上預測中,由于文獻[20]對初始輸出權值進行了遞推更新處理,故文獻[19]的線上預測復雜度要低于文獻[20],但是文獻[20]的預測性能要優于文獻[19]。新方法的計算復雜度略高于現有信道預測方法,但是新方法在線下訓練采用了深層ELM訓練網絡,線上預測利用新到來的信道信息來實時更新網絡的輸出權值,能夠獲得優于現有方法的預測性能,可以更好地適應信道的變化。

表1 不同信道預測方法的復雜度比較

4 結 論

針對HSR環境,本文提出了一種新型時變信道預測方法。基于單隱藏層神經網絡,新方法采用了堆棧式ELM來提取原始信道的深層特征,提高了預測的精度。此外,本文方法基于歷史信道樣本與初始的輸出權值來更新網絡的輸出權值,充分利用歷史信道信息,更新調整預測網絡的輸出權值,以使其更貼近當前的信道狀態,其進一步提高了信道預測的精度,適用于高速移動場景中時變信道信息的獲取。