在實踐中反思 在反思中優化
——以“環形跑道問題”為例

■陸祥雪 吳秋芳

知識與能力是教師專業發展的兩個方面。知識主要包括教育知識和學科知識兩個方面，這兩個方面融合為一體形成學科教學知識（簡稱PCK）。顧泠沅先生認為教學案例是發展PCK的重要載體。為了探求環形跑道問題中的相等關系，筆者先組織學生模擬跑，再用幾何畫板模擬實驗。通過不斷優化，發展了教師的教學能力，促進了教師的專業發展。

一、教學實施

問題1:運動場環形跑道周長400m，小紅跑步的速度是爺爺的倍，他們從同一起點沿跑道的同一方向同時出發，5min后小紅第一次與爺爺相遇。請問:小紅和爺爺跑步的速度各是多少？

這是蘇科版《數學》七年級上冊“用一元一次方程解決問題”中的問題4。教材在分析中直接給出這個問題的數量關系式：小紅跑的路程-爺爺跑的路程=400。

那么，教師在授課時，怎么來闡述這個相等關系呢？

師：這個問題中的相等關系是什么呢？

生1：第一次相遇時，小紅比爺爺多跑一圈。

師：你是怎么知道的？

（學生1沉默。）

師：好！為了驗證這位同學所說的相等關系，我們用幾何畫板做個模擬實驗。如圖1，我們用實心點表示小紅，空心點表示爺爺，為了方便區分，我們將小紅與爺爺的同一跑道，分離為兩個同心圓，不過我們認為它們的半徑是相同的。圖中的“動畫點”就相當于小紅與爺爺起跑的“發令槍”，我只要一點擊，兩個點就運動起來了。現在我開始點擊“動畫點”，請同學們注意觀察小紅比爺爺多跑了多少？

在學生觀看兩個點的運動的同時，教師手握鼠標，當實心點與空心點第一次相遇，再次點擊“動畫點”停止運動（如圖2）。

圖2

師：好！我們現在停止運動，請問，小紅與爺爺第一次相遇時，小紅比爺爺多跑了多少？

生1：多跑了一圈。

師：你是怎么知道的？

（學生1還是沉默。）

師：我們重新演示一遍。

師：當實心點（小紅）再次回到起點時（如圖3）（此時教師點擊“動畫點”按鈕，使兩點運動停止），此時實心點（小紅）已經跑了多少？

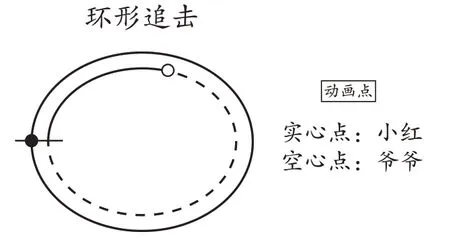
圖3

生1：一圈。

師：當實心點（小紅）第一次與空心點（爺爺）相遇時，小紅比爺爺多跑了多少？

生1：還是一圈。

師：請你解釋一下原因。

生1：因為從小紅再回到起點到追上爺爺（第一次相遇），小紅與爺爺跑的路程是相同的，而在此之前，小紅已經跑了一圈，所以小紅比爺爺多跑了一圈。

師：很好！那就請你到黑板上來完整地解答這個問題。

師：接下來我們再看一下這道題的變式題。如圖4，小明與小華在一個邊長為100米的正方形ABCD的跑道上練習跑步，小明的速度為每分鐘200米，小華的速度為每分鐘150米，小明、小華分別從A、B兩點同時出發，按順時針方向跑。請問：當小明和小華首次相遇時，此題的相等關系又是什么？

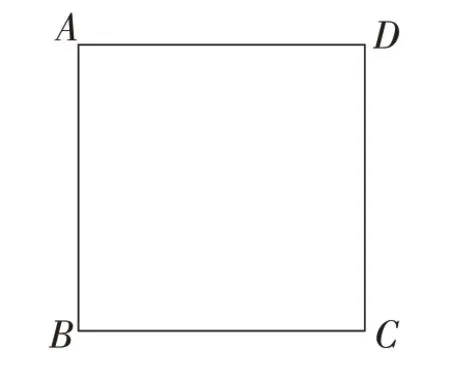
圖4

生2：小明比小華多跑了300米。

師：為什么？

生2：小明跑到小華的起點B時，小明跑了300米，當小明首次與小華相遇時，小明比小華多跑了300米。

師：同意的請舉手。

二、教學改進

起初，設計教學方案時，為了尋找相等關系，教師請兩名學生到講臺來，站在同一個位置。一名學生扮演“小紅”，另一名學生扮演“爺爺”，沿教室內的過道，來模擬跑。教師提醒學生注意觀察小紅比爺爺多跑了多少。于是，兩名學生在教室內跑了起來。教師問：“小紅是不是比爺爺多跑了一圈？”有學生說“是的”，但大多數學生不發聲。教師發現回答的人很少，就覺得可能有學生沒有看清，于是，又重新演示了一遍。當教師再次提問時，學生的回答還是很少，說明大多數學生沒有看清問題中的相等關系。

設計模擬跑的目的是用實際情境幫助學生尋找問題中的相等關系，提升學生的參與度，提高學習興趣。但學生并沒有通過這個模擬跑的實驗發現問題中的相等關系。另外，教師在學生沒有辦法說明“小紅比爺爺多跑一圈”的情況下，也沒有幫助學生解決這個疑惑，而是選擇避而不談。筆者對此教學設計進行反思，問題出在何處？在教室里模擬跑，學生的注意力僅是集中在兩個學生身上，而不能觀察到兩個學生的行進路徑。找到問題的癥結，筆者做出幾點改進。

改進的目標是化不可視的行進路徑為可視。于是，有了兩個改進的方案：一是用線示法，將小紅與爺爺跑的路線畫出來，如圖5，讓學生直觀地比較小紅比爺爺多跑了多少。在起點與相遇點之間，小紅與爺爺有一段路程是一樣的，如果我們把它們擦除，剩下的部分恰好是一圈。二是用幾何畫板來進行模擬實驗，這樣小紅與爺爺跑的路徑可視性更強，且不需要場地。

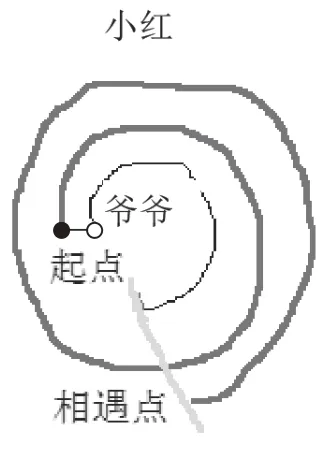
圖5

三、教學反思

從最初設計到優化后的最終設計，經歷了“設計—實施—反思—改進”的循環過程，這個過程不但提高了課堂教學效率，而且促進了教師自身發展。

1.“設計—改進”促進終身學習。

在“環形跑道問題”中，學生不能探索出相等關系，所以需要改進設計，打破原有的知識、思維框架，否則只能墨守成規，不斷退步。

現代教育技術已經得到了很大的發展，雖然知識是古老而陳舊的，但借助新技術，知識以新的面貌呈現。其實，只要用幾何畫板的動態演示就能解決這個問題。利用軟件對動點的追蹤功能，學生可以很全面地從整體上觀察兩人的跑步路徑，而不是在教室或操場上只能看到局部的情形。這就是PCK分類中的一類，即將特定的學習內容呈現給學生的策略知識。

2.“設計—改進”促進深度思考。

利用幾何畫板讓學生直觀地觀察小紅比爺爺多跑了一圈，但學生受路徑重疊的影響，效果反而不如圖5的“線示法”。學生在解決變式題時受挫，這都促使我們去反思，去進行更深度的思考，觸及問題的本質，由教師的深度思考去引導學生的深度學習。其實，這個模擬實驗，讓我們從直觀上獲得了感性知識，同時，還體現數學的理性特點。怎么說明這個從實驗中獲得的相等關系？這就需要教師在備課時做充分思考。我們為什么要從運動過程中抽出圖3，而不是僅僅出現起點與終點的圖1或圖2，目的就是為進行理性的解釋鋪路。當小紅再回到起點時，她已經跑了一圈，小紅從現在到與爺爺第一次相遇，兩人所跑的路程相同，所以小紅比爺爺多跑了一圈。根據學生回答的情況，可以多次重復演示，并在小紅回到起點時停留，讓學生觀察，找準觀察的對象。這實際上就是基于同一個起點，如何比較小紅和爺爺所跑路程的長短問題。學生在明晰這點之后，就可以扔掉“直觀”的拐杖，解決相關的變式題。實踐證明，教師利用改進優化后的方案實施教學，學生解答變式題的準確率提高很多。

3.“設計—改進”促進“四個理解”。

章建躍博士提出“理解數學、理解學生、理解技術、理解教學”。我們要充分掌握這四個“理解”間的關系，恰當地使用信息技術幫助學生理解數學內容。信息技術起輔助作用，還得結合學生的想象力。對七年級學生來說，形象思維占主導地位，所以我們通過幾何畫板來直觀、整體地呈現小紅及爺爺跑的過程，有助于學生突破難點，理解相等關系。教師應樹立終身學習的理念，與時俱進，只有常備一桶活水，方能澆灌新時代的花朵。