基于最佳子策略記憶的強化探索策略

周瑞朋，秦 進

（貴州大學計算機科學與技術學院，貴陽 550025）

0 概述

強化學習中存在探索與利用困境，一個強化學習智能體必須嘗試一些之前沒有嘗試過的操作，發現其中某些能有效產生獎勵的動作，同時智能體也必須充分利用能有效產生獎勵的經驗［1］。強化學習問題中的ε-greedy 策略由于簡單而被廣泛使用，但在這種探索策略下智能體過度依賴于隨機算子，探索完全隨機，沒有針對性。目前已有大量關于強化學習中有效探索的研究，如2002 年KEARNS 等［2］提出的多項式時間內的近最優強化學習，2010 年JAKSCH 等［3］提出的強化學習的近最優后悔邊界。多數探索方法都依賴于隨機干擾智能體的策略，如1999 年SUTTON 等［4］提出的ε-greedy，WILLIAMS［5］提出熵正則化以誘導新動作，但這些方法都限制于較小的狀態動作空間或者線性函數近似，不適用于神經網絡 這樣的復 雜函數近 似［6］。2016 年BELLEMARE 等［7］提出基于 計數的探 索，2017 年OSTROVSKI 等［8］提出狀態空間的密度建模，這些方法被嘗試用來解決高維度和連續動作上的馬爾科夫決策問題，但不足是它們都依賴于較為復雜的額外結構，且探索不具備針對性。2017 年PATHAK 等［9］提出的自監督好奇心模塊，通過建立一個環境預測模型，對于模型預測不佳的，給予智能體一定的獎勵（好奇心），這種方法在某些控制問題上有一定的效果，但是在部分控制問題上會導致智能體陷入過度探索。另一種方法是通過向算法中加入額外的關聯噪聲來增加自然探索，如2017 年MATTHIAS 等［10］提出使用參數空間噪聲探索，2018 年FORTUNATO等［11］提出噪聲網絡探索。這些算法通過加入噪聲干擾神經網絡計算動作的Q值，從而影響智能體在當前狀態下采取的動作，這些動作可能是之前沒有嘗試過的動作。2020 年ZHANG 等［12］提出與任務無關的探索策略，通過探索MDP，不依賴于獎勵函數去收集軌跡。這些算法一定程度上提高了算法效率，但是過度依賴隨機算子，干擾神經網絡計算動作的Q值，其探索動作沒有針對性，在探索期間，如果智能體訪問到某些對于獲取獎勵沒有幫助的狀態，在這些策略下，它可能會繼續深度探索這些狀態及其后繼狀態，產生過度探索的問題。

在有限馬爾科夫決策過程中，存在一個唯一的、確定的最優策略π*，其狀態動作值函數Q*對于所有狀態動作對都是最優的［13］，這個最優值函數滿足貝爾曼最優性方程集。受此啟發，筆者認為最優策略由若干局部最優策略組成。在強化學習中，一個學習任務被建模成馬爾科夫決策［14］過程，那么其局部最優策略空間不可能無限大，則設計一個基于獎勵排序的M 表，通過訓練不斷迭代最后得到一個最優策略的最優子策略空間。

本文設計基于獎勵排序的M 表并改進ε-greedy算法。智能體在一定的概率下對當前樣本與M 表中子策略進行匹配，若找到一個相似子策略，則選擇該策略所采用的動作，通過這種方式，使智能體得到的動作具有針對性，同時提高獲得的平均獎勵。

1 基礎理論

1.1 深度強化學習

強化學習是用于解決序貫決策的機器學習分支領域，其關鍵之一是智能體要學習好的行為，這意味著需要增量式地調整行為或獲得新的技巧。另一個關鍵是強化學習通過不斷試錯獲取經驗進而學習［15］。強化學習問題通常被建模成馬爾科夫決策過程，在每個時間步t，智能體所處狀態為st，策略π(at|st)表示智能體在狀態st下執行動作at的概率，在此概率下執行動作at，獲得一個標量獎勵rt，并轉換到st+1，將這個過程用五元組(st，at，st-1，rt-1，done)表示，其中done 是個布爾值，用來指示一個episode 是否結束。在回合型問題中，其回報是帶折扣的累積獎勵，折扣因子γ∈(0，1]，是對未來預估獎勵的懲罰項：

智能體的目標就是最大化每個狀態的長期回報期望。通常使用值函數來預測未來回報的期望以衡量一個狀態或者狀態動作對的好壞。狀態值函數定義為：

動作值函數定義為：

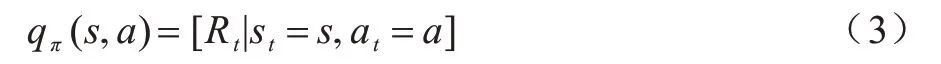
一個最優狀態值被定義為：

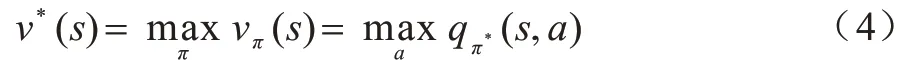
深度強化學習就是使用深度神經網絡來近似強化學習中的狀態值函數（或動作值函數）。深度強化學習被廣泛應用于視頻游戲［16］、機器人［17］、自然語言處理［18］、計算機視覺［19］等領域。2013 年，DeepMind團隊將深度神經網絡引入強化學習用來近似值函數。深度強化學習設置了經驗緩沖，將智能體與環境進行交互產生的經驗存入該緩沖，通常又稱這些經驗為樣本。

1.2 ε-greedy 探索策略

ε-greedy 策略是強化學習中最常用的探索策略。在該策略下，智能體有ε的概率會選擇一個隨機動作，1-ε的概率選擇當前動作Q值最大的動作，定義為：

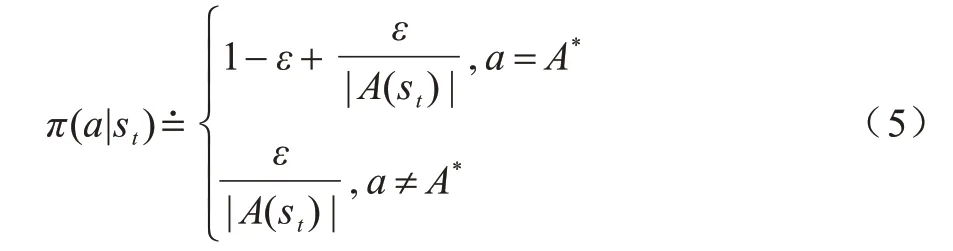
其中：A*表示最優動作；|A(st)|是當前狀態st下所有可選動作的集合。

2 基于最佳子策略記憶的強化探索

定義一個強化學習問題的狀態集為：

π*表示全局最優策略，由有限馬爾科夫決策過程的性質可知其由若干優先的局部最優子策略組成。本文使用(st，at)表示子策略，用來近似π*，是一個向量。定義為：

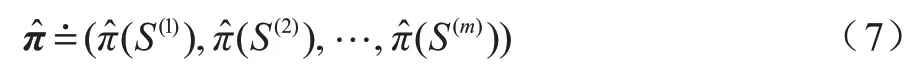
基于最佳子策略記憶的強化探索，就是將智能體目前學到的最佳子策略存入一個存儲表中（記為M 表），當智能體訪問M 表時，將當前狀態與M 表中子策略狀態進行相似度計算。若構成相似，則返回子策略中的動作。

2.1 基于獎勵排序的M 表

解決過度探索，一個可行的方法是增加探索的針對性。在智能體與環境交互過程中，會產生大量的樣本并將樣本保存到經驗緩沖中。本文將較好的經驗作為子策略獨立存放，在探索時，以一定的概率計算智能體當前狀態與這些子策略的相似度，類似基于實例的學習，本文選擇最相似的子策略中的動作并執行。通過相似計算增加智能體產生新的獎勵值較高的樣本的概率，這樣的探索能夠促進智能體獲得獎勵值大的樣本，使探索具有針對性。如果將所有的子策略保存下來，那么空間開銷和計算代價將會很大。本文使用結構性相似度算法計算子策略的相似度，將相似的子策略中獎勵值最高的子策略存入M 表中，視為智能體目前學到的最佳子策略。M 表獨立于經驗緩沖和智能體對經驗的采樣過程。M 表使用二元組(st，at)來存儲一個最佳子策略，并為每個子策略附加一個獎勵信息rt，表示該子策略可獲得的獎勵，并使表中所有子策略基于獎勵降序排序。M 表上的操作如圖1 所示。

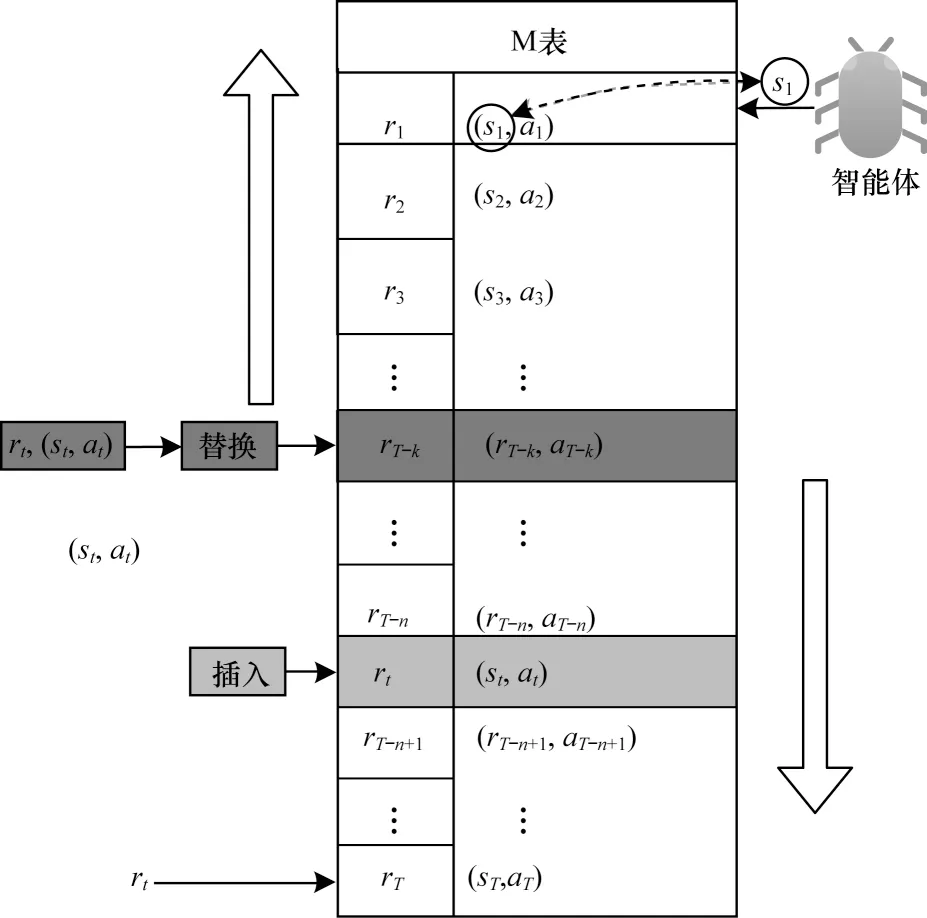
圖1 M 表上的操作Fig.1 Operation on table M

如圖1 的左邊部分所示，智能體與環境交互產生一個新樣本之后，如果樣本的獎勵值大于零且M 表為空，則將該樣本中的子策略存入M 表。若M 表不為空，則依次判斷該獎勵與倒序的M 表中子策略的獎勵值。若該獎勵大于某個子策略(sT-k，aT-k)的獎勵且小于該子策略的前繼子策略(sT-k-1，aT-k-1) 的獎勵，則進一步計算該樣本與(sT-k，aT-k)中狀態的相似度，若小于閾值θ，則認為不相似并掃描(sT-k+1，aT-k+1)前面的子策略中是否有與其相似的子策略，如果有，則跳過該策略，如果沒有相似度且大于閾值θ，則認為相似，并使用樣本中的子策略替換掉M 表中對應的子策略(sT-k，aT-k)，可結合圖1 中3 個綠色文本框和上下子策略查看（彩色效果見《計算機工程》官網HTML 版）。若樣本中的子策略(st，at)獎勵值大于(sT-n+1，aT-n+1)的獎勵且小于(sT-n，aT-n)的獎勵，M 表中沒有與其重復的子策略（若有重復，則跳過），且該子策略與(sT-n+1，aT-n+1)不相似，則將其插入(sT-n，aT-n)與(sT-n+1，aT-n+1)之間，可結合圖1 中紅色文本框以及上下子策略查看（彩色效果見《計算機工程》官網HTML 版）。

如果該樣本的獎勵大于零但不大于M 表最后一個子策略的獎勵，則檢查M 表前面是否有與其相似的子策略，若有，則跳過該樣本，反之，則將該樣本中的子策略添加到M 表的末尾。

基于最佳子策略記憶的強化探索設計智能體在探索時，將有一定的概率會通過M 表進行探索。在這種情況下，智能體會對M 表做相似查詢，通過將當前狀態與M 表中子策略的狀態正序依次計算相似度。若與其中某個子策略的相似度大于θ，則將該子策略中的動作反饋給智能體。如圖1 右半部分所示，若st與s1相似，則將該動作反饋給智能體，若不相似則繼續往下找，若整個M 表都沒找到，智能體將選擇神經網絡計算該狀態下最大Q值的動作。

2.2 MEG 探索

在通常情況下，強化學習算法采用ε-greedy 探索。本文在ε-greedy 算法的基礎上加以改進得到M-Epsilon-Greedy（MEG）探索。

令am為從M 中選出的最佳動作，aQ為利用神經網絡選出的動作，am和aQ不同。A 為智能體所有可選動作。智能體從M 表中選出的一個動作為，sim 函數用來求智能體當前狀態與M 中子策略狀態的相似度，從M 表頭到表尾，如果小于θ，則取對應子策略中的動作。由于前期神經網絡不穩定，為了使智能體在前期保留探索能力的同時增強探索的針對性，本文將智能體利用神經網絡的概率分出一部分使用M 表探索，這樣智能體就既保留了探索能力，又能夠有效結合目前已學最佳策略進行探索。

由此，定義MEG 探索表示為：

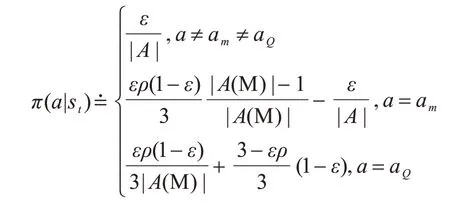
在狀態st下，智能體以ε的概率選擇一個隨機動作a，以的概率選擇對M 表進行相似查詢，ρ為在M 表中找到相似子策略的概率，如果找到相似子策略，則選擇子策略中的動作am，反之，則選擇神經網絡計算出最大Q值的動作。在的概率下選擇利用神經網絡計算的Q值最大的動作aQ，其中|A(M)|為M 表中所有動作的集合，|A|為智能體在該環境下的所有動作集合，探索概率設置將在下文3.1 節中詳細介紹。

MEG 探索示意圖如圖2 所示。

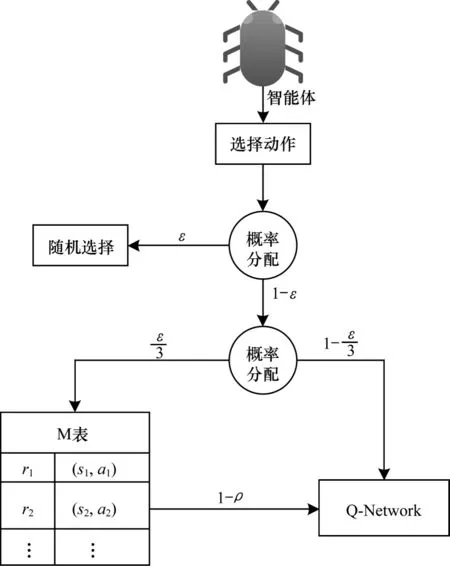
圖2 MEG 探索示意圖Fig.2 Schematic diagram of MEG exploration

2.3 訓練

基于最佳子策略記憶的強化探索方法具有廣泛適用性，為了驗證其性能，本文使用FQF 算法［20］（分布強化學習的全參數分位數函數）作為實例。

將基于獎勵的有序M 表和MEG 探索策略與FQF 相結合，得到M-FQF。定義經驗緩沖的容量為N，每一次訓練所用的數據量為一個batch_size。一個強化學習問題從開始到結束為一個episode。

為近似分位點函數網絡，為分數提議網絡設置H個可調分位數（τ0=0，τH=1）。分數提議網絡輸出對應的分位數并將這些分位數傳入分位點函數網絡。分位點函數網絡將每個狀態動作對映射到對應分位數的概率，使用1-Wasseretein 計算近似分位點函數與真實分位點函數分布之間的距離，為了最小化1-Wasserstein 誤差，從固定的可調分位數τ去尋找對應的最優分位數值。分別使用RMSprop 算法和Adam 算法優化分數提議網絡和分位點函數網絡。將分布貝爾曼更新和分位數回歸相結合訓練分位點函數網絡，最小化Huber 分位數回歸損失（同分布強化學習的隱分位數網絡IQN［21］和分位數回歸的分布強化學習QR-DQN［22］，將閾值設為k）。達到訓練的最低步數后，對樣本采樣，訓練網絡。最后更新分數提議網絡和分位點函數網絡。

3 實驗與分析

3.1 實驗設計

為驗證改進策略的有效性，選擇Playing Atari 2600游戲中的經典控制問題BankHeist、RoadRunner、Freeway、BeamRider作為實驗對象，將本文改進算法與DQN系列算法以及非DQN系列的A2C算法［23］進行比較。

軟件環境：Arcade Leaning Environment，CUDA10.0，Pytorch 1.5，Python3.8。硬件環境：GPU型號：Tesla P40 以及NVIDIA GeForce RTX 2080 Ti。為公平比較，對BankHeist、RoadRunner、Freeway、BeamRider 使用同狀態對抗DQN的魯棒深度強化學習［24］（SA-DQN）的參數，訓練了500萬個step。圖中橫坐標單位為250 000 step。對于Playing Atari 2600 視頻游戲設置250 000 step 視頻游戲幀用于探索。本文使用IQN、FQF、QR-DQN、IQNRAINBOW［25］這4 種算法作為baseline。經驗回放的大小設置為1 000 000，一個訓練batch_size 設置為32。折扣因子γ初始化為0.99。由于訓練之初神經網絡不穩定，如果利用神經網絡這種不穩定性去探索顯得沒有針對性，因此從中分出的概率，使智能體根據M 表來探索。這一方面不影響智能體以ε的概率探索動作空間，另一方面也加強了智能體探索的針對性。使用M表探索的概率隨著智能體探索概率ε線性衰減而逐漸衰減到0.01。初始化α=1e-5，θ=0.989。探索策略中的探索概率初始化為1，隨著訓練逐漸減少到0.01。目標網絡的更新步長C為10 000。對環境Arcade Learning Environment 所反饋的獎勵做歸一化處理后將樣本存入經驗緩沖。在與A2C 算法的比較中，選擇Berzerk、BeamRider這2種控制問題作為實驗對象。利用openAI的開源baselines 項目中的A2C 算法作為baseline，時間步與M-FQF 同為500 萬，其他參數為默認參數，epsilon為1e-5，alpha 與gamma 皆為0.99，學習率7e-4，智能體的評估間隔設置為250 000 step。

根據FQF 的實驗描述，設計以下實驗過程：智能體每到達一個狀態s就會將狀態輸入基礎DQN 經典網絡。該網絡將狀態s的特征傳遞給分數提議網絡，將輸出的所有動作輸入到分位點函數網絡。智能體根據MEG 探索策略選擇動作，以ε的概率會執行一個隨機動作的概率智能體從M 表中進行相似查詢選擇與當前狀態相似的子策略中的動作。以的概率選擇分數提議網絡預測的最大狀態動作值執行動作a，環境反饋獎勵和下一個狀態后，將產生的樣本存入經驗回放，再進行采樣、訓練。

3.2 實驗結果與分析

深度強化學習中算法效果主要由獎勵值決定。網絡在設定的迭代次數結束后，平均獎勵越大說明該算法的性能越好。M-FQF 在實驗環境Arcade Learning Environment 中4 種控制問題上的實驗結果如圖3～圖7 所示（彩色效果見《計算機工程》官網HTML 版）。

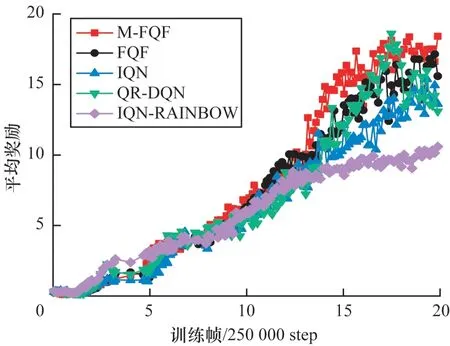
圖3 5 種算法在BankHeist 上的平均獎勵Fig.3 Average reward of five algorithms on BankHeist

通過實驗對比發現，結合了基于獎勵有序的M表探索策略 的FQF 算法（M-FQF）相較于FQF、IQN、QR-DQN、IQN-RAINBOW 算法，在多數控制問題上取得了更高的平均獎勵且具有更好的穩定性。

圖3 中約1.25×2 500 000 step 處5 種算法 突然性能變化較大，這可能是剛好更新了目標網絡，這時候更能體現算法本身的穩健性。IQN-RAINBOW 在經過這個點后就趨于平穩，獲得的平均獎勵是5 種算法中最低的。M-FQF 和FQF 趨勢有點相似，但是從圖中可以看出M-FQF 明顯要優于FQF 以及其他3 種算法。圖4 中游戲開局5 種算法的起點都不在原點，這是因為Freeway 游戲開局距離游戲得分處有一小段距離。約在2.5×250 000 step 到4×250 000 step 之間應該是智能體學習的一個關鍵階段。因為在這里5 種算法出現了不同程度的波峰或者波谷，只有QR-DQN 形成了一個波谷。相比其他4 種算法，QR-DQN 似乎受影響更大。可以看出這個問題上最優的算法是IQN-RAINBOW，其次是M-FQF。此外，5 種算法在Freeway 上都有較好的收斂性。

圖4 5 種算法在Freeway 上的平均獎勵Fig.4 Average reward of five algorithms on Freeway

在RoadRunner 問題上，從圖5 看出M-FQF 和IQN-RAINBOW 都有較好的收斂性。IQN-RAINBOW收斂更快，在初期其平均獎勵更高，但是其收斂的平均獎勵明顯低于M-FQF。M-FQF在該問題上表現最好。從圖6 可以看出，M-FQF 在該問題上收斂較為緩慢，但是最后獲得了較高的平均獎勵，說明其學習到了一個較好的策略。而IQN-RAINBOW 依然收斂最快，但是收斂的平均獎勵并不高且穩定性不好，出現了很多明顯的波峰和波谷。M-FQF 則相對穩健，整個訓練過程沒有出現明顯的波峰和波谷。Berzerk 問題的訓練情況如圖7 所示，M-FQF 和IQN-RAINBOW 收斂都很快，初期IQN-RAINBOW就獲得了最高平均獎勵，比M-FQF還稍高一些。但在5×250 000 step 后IQN-RAINBOW就趨于收斂了，與其同時，其他3 種算法也都趨于收斂，而M-FQF 平均獎勵還在不斷上升，最后獲得了最高的平均獎勵。可以看出，在Berzerk 問題上，M-FQF 算法性能最優，QR-DQN 性能最差。

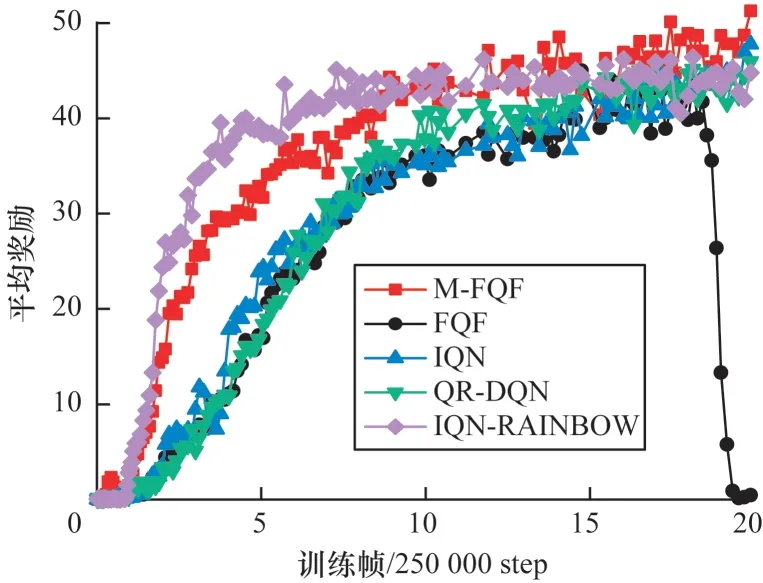
圖5 5 種算法在RoadRunner 上的平均獎勵Fig.5 Average reward of five algorithms on RoadRunner

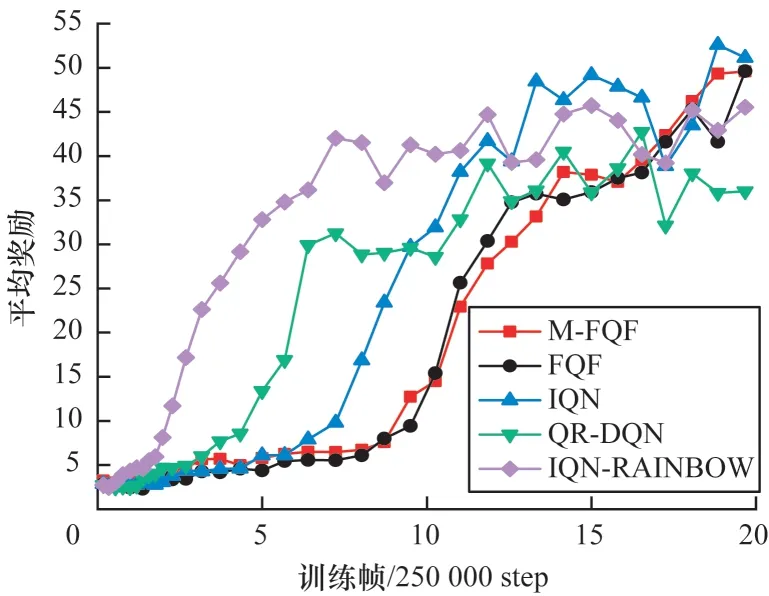
圖6 5 種算法在BeamRider 上的平均獎勵Fig.6 Average reward of five algorithms on BeamRider

圖7 5 種算法在Berzerk 上的平均獎勵Fig.7 Average reward of five algorithms on Berzerk

將M-FQF 與非DQN 系列算法的A2C 進行比較，如圖8 和圖9 所示。

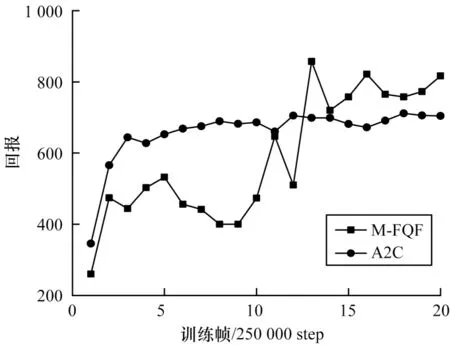
圖8 M-FQF 和A2C 算法在Berzerk 上的回報Fig.8 Return of M-FQF and A2C algorithms on Berzerk

圖9 M-FQF 和A2C 算法算法在BeamRider 上的回報Fig.9 Return of M-FQF and A2C algorithms on BeamRider

從圖8 可以看出，Berzerk 問題上A2C 算法收斂很快，在2.5×250 000 step 左右已經獲得較高的回報。反觀M-FQF 算法在1.25×2 500 000 step 之前尚未表現出收斂，1.25×2 500 000 step 以后M-FQF 算法反超A2C 算法，獲得了相對高的回報。圖9 中A2C 算法趨于平穩，而M-FQF 算法獲得了相對高的回報。可以看出A2C算法相對穩定，而M-FQF算法相對有些波動，不夠穩定。

除了與以上算法進行比較，本文對比了加入MEG探索和加入噪聲網絡以及優先經驗回放在Bankheist和Roadrunner 問題上的性能，如圖10 和圖11 所示（彩色效果見《計算機工程》官網HTML 版），可以看出，加入了MEG 探索的FQF 算法性能明顯提高。

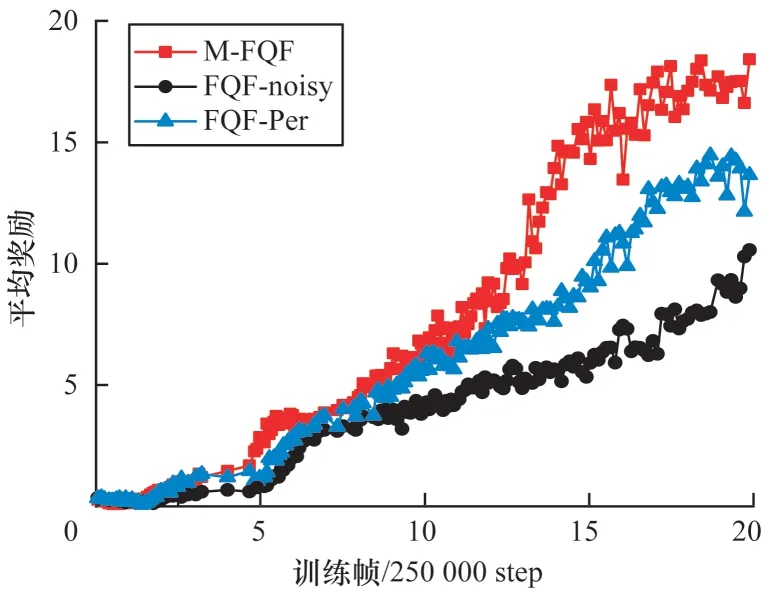
圖10 FQF 算法在BankHeist 上的平均獎勵Fig.10 Average reward of FQF algorithms on BankHeist

圖11 FQF 算法在RoadRunner 上的平均獎勵Fig.11 Average reward of FQF algorithms on RoadRunner

為測試MEG 探索是否對收斂結束時的參數值有依賴，在BankHeist 環境下做了4 個實驗，設置算法收斂過程中使用隨機探索和MEG探索的概率之和為0.01。用e表示隨機探索的概率，m表示使用MEG 探索的概率。M-FQF 不同探索參數的平均獎勵如圖12 所示（彩色效果見《計算機工程》官網HTML 版）。

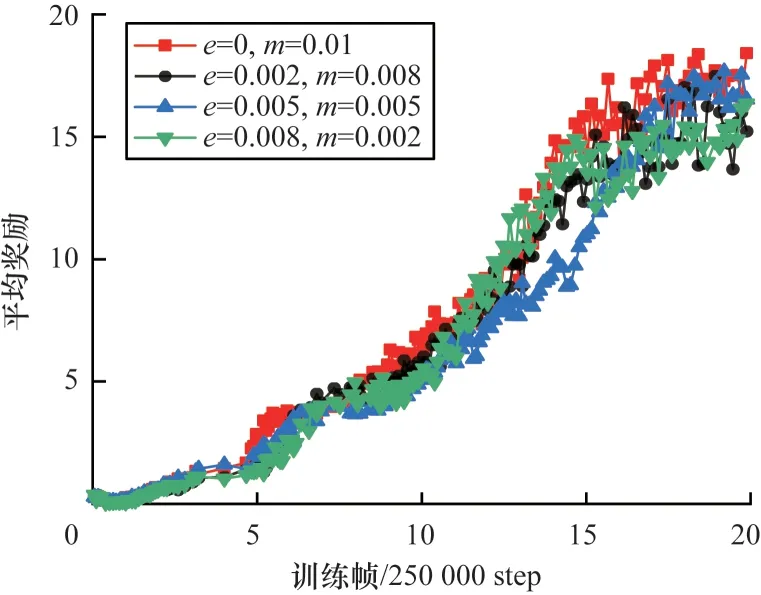
圖12 M-FQF 算法在BankHeist 上的平均獎勵Fig.12 Average reward of M-FQF algorithm on BankHeist

可以看出，隨著智能體使用MEG 探索的概率從0.01 下降到0.002，智能體所獲得的平均獎勵也在不斷減少，說明M-FQF 算法對于收斂過程中MEG 探索的概率參數設置有所依賴，使用MEG 探索的概率越大，算法性能越好。

4 結束語

本文設計一個基于獎勵排序的M 表，進而提出基于M 表的MEG 探索策略，并都加入到FQF 算法中，以提高算法的探索效率，緩解過度探索的問題。實驗結果表明，該策略在Playing Atari 2600 游戲中取得了較高的平均獎勵。但MEG 探索依然存在不足，如在部分游戲中收斂速度緩慢。下一步將針對此問題，通過調整探索方法進一步優化MEG 探索效果，如將M 表中實際存在的最佳子策略個數和有效訪問次數考慮在利用M 表進行探索的概率計算過程中，或對M 表中的最佳子策略進行路徑規劃，通過邏輯處理導出新的最佳子策略或啟發策略。