考慮混合約束的柔順機構拓撲優化設計

占金青， 王云濤， 劉 敏， 朱本亮

(1.華東交通大學 機電與車輛工程學院，南昌 330013;2.華南理工大學 廣東省精密裝備與制造技術重點實驗室，廣州 510641)

柔順機構是通過其柔性組件的變形來實現運動、力傳遞或能量轉換的一種整體式機構[1-2]。柔順機構對裝配過程的需求降至最低，同時它能夠減少摩擦、磨損及潤滑，具有高精度和高適應性優點。因此，柔順機構在精密加工、微納操作及微機電系統等許多領域應用廣泛[3-5]。

基于拓撲優化方法設計的柔順機構構型的特征尺寸有時太小，難以加工制造，并且容易引起應力集中現象，導致疲勞壽命降低。因此，考慮最小尺寸控制進行柔順機構拓撲優化設計是非常有必要的。Guest等[6-7]采用Heaviside函數的映射方法進行實相材料最小尺寸控制的結構拓撲優化設計；在此基礎上，提出了一種多相映射拓撲優化方法，能夠實現實相和空相兩相材料結構最小尺寸控制。榮見華等[8]采用兩種不同的Heaviside映射分布過濾實相和空相設計變量，進行考慮最小尺寸控制的結構拓撲優化設計，獲得的拓撲結構清晰。Sigmund[9]引入基于圖形學中侵蝕和擴張算子的映射方法，實現了結構的實相和空相最小尺寸控制。Wang等[10]提出了一種基于侵蝕、中間和擴張映射的拓撲優化魯棒性列式，可以同時控制實相和空相的最小尺寸，但是每次迭代需要進行多次有限元分析，導致計算成本增加。Zhou等[11]提出了一種基于幾何約束的最小尺寸控制拓撲優化設計方法。

為了滿足機構的靜強度要求，需要考慮應力約束進行柔順機構拓撲優化設計。Saxena等[12]采用基結構法進行基于局部應力約束的柔順機構拓撲優化設計，計算成本高。Chu等[13]采用參數化水平集方法進行多相材料柔順機構應力約束拓撲優化設計。Lopes等[14]采用拓撲導數方法進行柔順機構應力約束拓撲優化設計。Leon等[15]考慮全局應力約束進行柔順機構拓撲優化設計，以滿足機構的靜強度要求。占金青等[16]采用P范數方法進行柔順機構應力約束拓撲優化設計。Pereira等[17]研究了不同應力極限約束值及靈敏度過濾半徑對柔順機構拓撲優化結果的影響規律。

目前，現有研究僅僅單獨考慮制造約束或應力約束進行柔順機構拓撲優化設計，沒有綜合考慮制造約束和應力約束進行柔順機構混合約束拓撲優化設計。本文提出一種綜合考慮最小尺寸控制和應力約束的柔順機構混合約束拓撲優化設計方法。采用改進的固體各向同性材料插值模型描述材料分布，利用多相映射方法同時控制實相和空相材料結構的最小尺寸，采用最大近似函數P范數求解機構的最大應力，以柔順機構的輸出位移最大化作為優化目標，建立綜合考慮最小尺寸控制和應力約束的柔順機構混合約束拓撲優化模型，利用移動漸近優化算法進行混合約束拓撲優化問題求解，通過數值算例對本文提出的方法的有效性進行驗證。

1 柔順機構混合約束拓撲優化模型

1.1 材料插值模型

對于柔順機構混合約束拓撲優化問題，采用改進的SIMP(solid isotropic material with penalization)材料插值模型[18]描述結構的材料分布，其表示為

(1)

式中：Ee為單元e的材料彈性模量；φi為單元設計變量；k為懲罰系數，取值為3；E0和Emin分別為實體材料和空洞材料的彈性模量；φmax和φmin分別為設計變量的最大值和最小值。

1.2 最小尺寸控制

多相映射方法[19]采用Heaviside函數將設計變量場映射到物理變量場，無需添加額外的約束條件，能夠實現實相和空相材料結構的最小特征尺寸控制；因此采用多相映射方法進行柔順機構構型的最小制造尺寸控制。

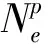
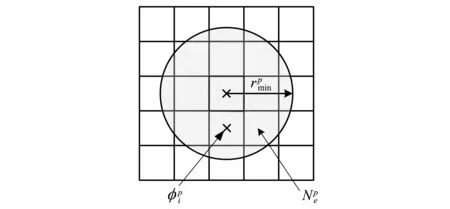
圖1 多相映射示意圖Fig.1 Schematic of multiple phase projection

(2)

式中，xi為單元i的中心坐標。

(3)

式中：ωp為雙曲線正切的非線性函數；ω為常數權重函數，表示為

(4)

對于實相和空相材料，非線性函數ωp分別取為

(5)

(6)

式中，αs和αv為可調參數，分別取為2×10-3和5×

10-4。

定義φrange=φmax-φmin，用來計算np

(7)

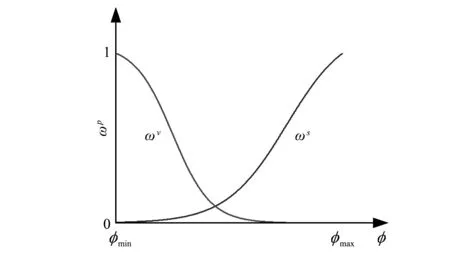
圖2 非線性函數ωp曲線圖Fig.2 The nonlinear weighting function ωp

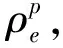
(8)

式中，β為控制近似程度的參數，當β=0時，映射函數相當于線性映射，當β趨近于∞時，映射函數趨近于Heaviside階躍函數。

(9)

1.3 應力約束

結構有限元分析中，任一單元e的應力可表示為

σe=DBue=[σ11,σ22,σ12]T

(10)

式中：σe為單元的應力列陣；D為材料的彈性矩陣；B為應變位移矩陣；ue為單元節點位移列陣；σ11和σ22分別為單元x和y方向的主應力；σ12為單元的剪切應力。

為了避免應力約束引起的奇異解問題，采用應力松弛方法[22]進行單元應力懲罰，因此，任一單元e的von Mises等效應力表示為

(11)

式中：q為松弛系數，取值為0.5；σvM為未松弛的e單元的von Mises等效應力；V為輔助矩陣，其表示為

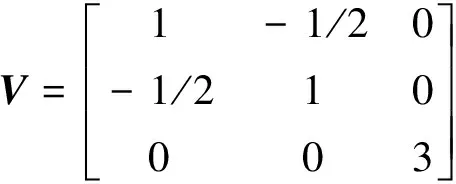
(12)

將機構的設計區域離散成有限個單元，每個單元對應一個局部應力約束，引起總的約束數太大，使靈敏度分析計算量巨大。為了提高計算效率，采用P范數方法[23]將所有單元的局部應力約束進行最大近似處理，轉變為全局的應力約束問題。P范數應力σPN可表示為

(13)

式中：P為P范數參數；ve為單元體積。

當P的值趨近于∞，P范數應力值趨近最大的應力值，但是，P的取值過大，容易引起非線性程度越明顯，甚至導致優化迭代求解困難。然而，P取值過小，引起P范數應力與最大應力在數值上的差異較大。因此，為了減少兩者在數值上的差異，采用自適應約束縮放方法[24]修正P范數應力

σmax≈γσPN

(14)

式中，γ為自適應約束縮放系數。

當迭代步數n≥1，γn可表示為

(15)

式中：ζn為控制參數，取值為ζn=0.5；γ0=1。

1.4 拓撲優化模型

采用多相映射方法進行拓撲優化實體和空相材料結構的最小尺寸控制；將柔順機構輸出端的位移最大化作為優化目標函數，以滿足機構的運動需求；以機構的應力作為約束，以滿足靜強度指標；綜合考慮最小尺寸控制和應力約束，建立柔順機構混合約束拓撲優化數學模型為

(16)

2 靈敏度分析及優化算法

采由式(16)，機構的輸出位移對設計變量的靈敏度可求得為

(17)

(18)

由式(9)對設計變量求導，式(18)中的?ρe/?φi項可求得為

(19)

(20)

(21)

式(21)右端的?ωp/?φi項可由式(5)和式(6)分別對設計變量求導得到

(22)

(23)

由式(16)，體積約束的靈敏度可求得

(24)

由式(14)，最大應力σmax對設計變量的靈敏度可求得

(25)

對式(25)等號右邊的各項進行求解，則有

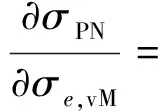
(26)

(27)

由式(11)和式(12)，式(27)右邊的?σvM/?σe項可求得為

(28)

單元應力矢量σe對單元密度ρe的靈敏度可由式(10)求得

(29)

將式(28)和式(29)代入式(27)可得

(30)

令有

(31)

將式(26)、式(30)及式(31)代入式(25)中，可得最大應力對設計變量的靈敏度為

(32)

令有伴隨矢量λ滿足

(33)

式中，Ke為單元的剛度矩陣。

由式(33)，式(32)改寫為

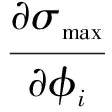
(34)

移動漸近線優化算法[25](method of moving asymptotes，MMA)適用于復雜的多約束優化問題求解，具有較好的魯棒性。因此，采用MMA算法求解基于混合約束的柔順機構拓撲優化設計問題。

3 數值算例

本章通過反向器和咬合機構兩個數值算例來驗證本文提出的柔順機構混合約束拓撲優化設計方法的有效性。所有算例中，實體材料選用Al7075，材料的彈性模量E0為68.9 GPa，空洞材料的彈性模量Emin為10-4；屈服強度為275 MPa，泊松比為0.33。單元設計變量的初始值均取值為-0.3；控制參數β的初始值取為1，每間隔50迭代步增大1倍，最大值為16；P范數參數P取值為8。

3.1 反向器

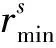
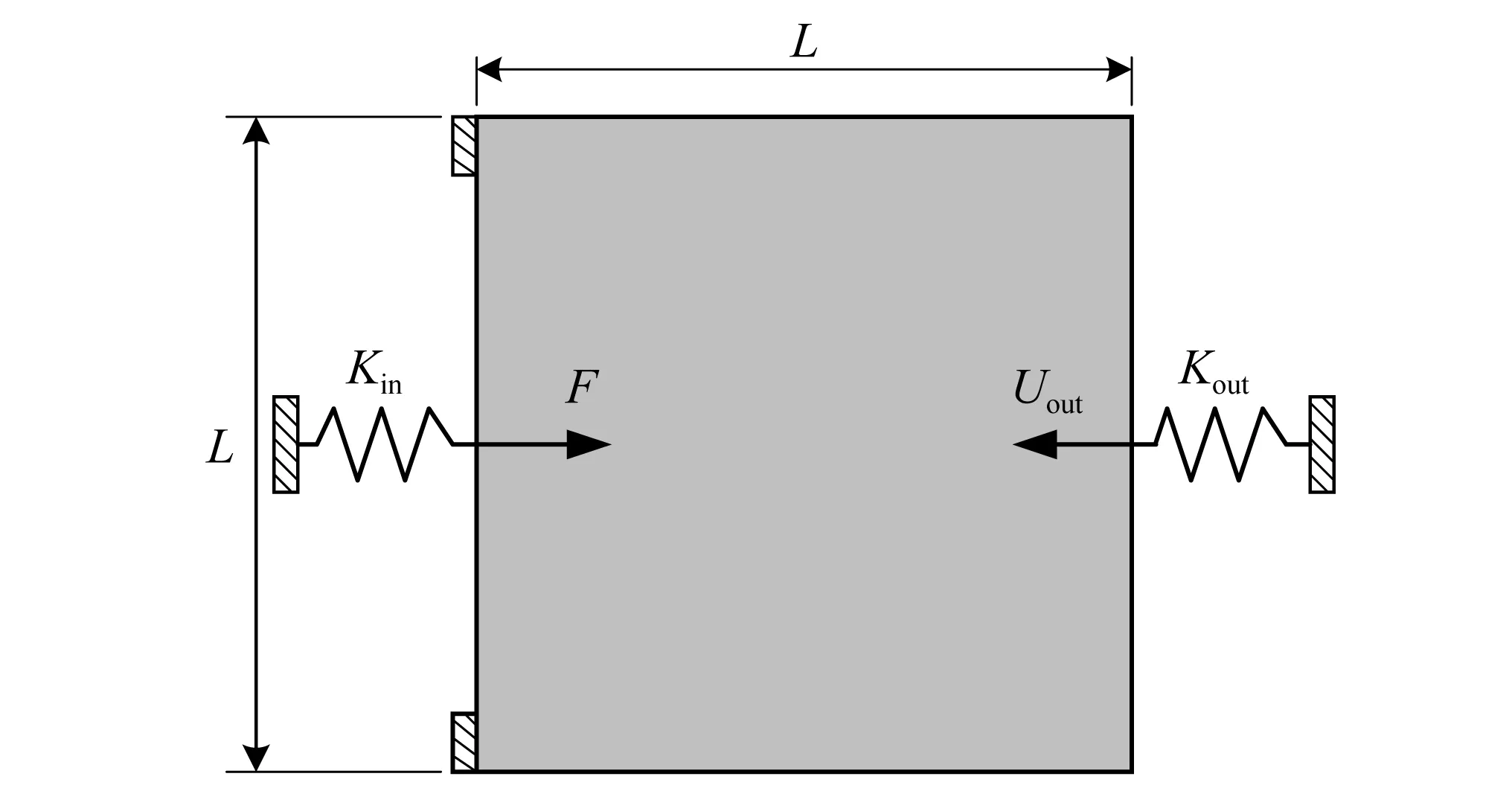
圖3 柔性反向器設計域Fig.3 Design domain for compliant inverter mechanism

為了驗證提出的方法有效性，在相同設計參數條件下，采用無最小尺寸控制、無應力約束，有最小尺寸控制、無應力約束，無最小尺寸控制、有應力約束，有最小尺寸控制、有應力約束四種拓撲優化模型進行柔性反向器設計，反向器的拓撲優化結果分別如圖4～圖7所示。

圖4 無最小尺寸控制、無應力約束的反向器拓撲優化Fig.4 Topological design of inverter mechanism without minimum length scale control and without stress constraints

無最小尺寸控制、無應力約束拓撲優化獲得的柔性反向器拓撲構型存在實相和空相細小尺寸特征，最大應力值(480.123 MPa)出現在變形較大的單節點連接鉸鏈區域，結構的應力集中現象非常明顯。有最小尺寸控制、無應力約束拓撲優化獲得的反向器構型的實相和空相材料結構能夠滿足最小尺寸要求；最大的應力值為425.598 MPa，表明添加最小尺寸控制可以在一定程度減少機構的應力水平，但是應力集中現象仍然明顯。

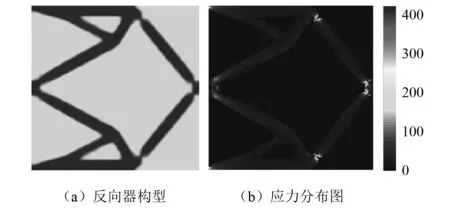
圖5 有最小尺寸控制、無應力約束的反向器拓撲優化Fig.5 Topological design of inverter mechanism with minimum length scale control and without stress constraints

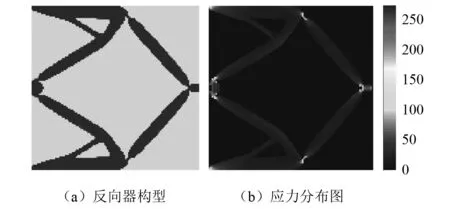
圖6 無最小尺寸控制、有應力約束的反向器拓撲優化Fig.6 Topological design of inverter mechanism without minimum length scale control and with stress constraints

與無最小尺寸控制、無應力約束拓撲優化結果相比，無最小尺寸控制、有應力約束拓撲優化獲得的反向器構型的最小特征尺寸有所變大，但是實相和空相的最小特征尺寸仍然過小，不易加工制造。機構的最大應力值為274.995 MPa，小于材料的屈服極限值，因此能夠滿足機構的靜強度要求，并且應力分布更加均勻。

考慮最小尺寸控制和應力約束的混合約束拓撲優化獲得的反向器構型的實相和空相材料結構能夠滿足最小尺寸要求，有效地避免細小幾何特征的出現，有利于加工制造；結構的應力最大值為275.025 MPa，很好地滿足應力約束，結構應力分布相對均勻，因此能夠同時滿足最小制造尺寸約束和靜強度要求。由表1可知，與其他的三種拓撲優化模型優化結果相比，混合約束拓撲優化獲得的柔性反向器的輸出位移最小，由于最小尺寸控制和應力約束的混合約束在一定程度上限制了輸出位移的最大化。反向器混合約束拓撲優化迭代過程中，初始階段會出現應力約束違反現象，造成一些波動，總體迭代過程平穩，如圖8所示。

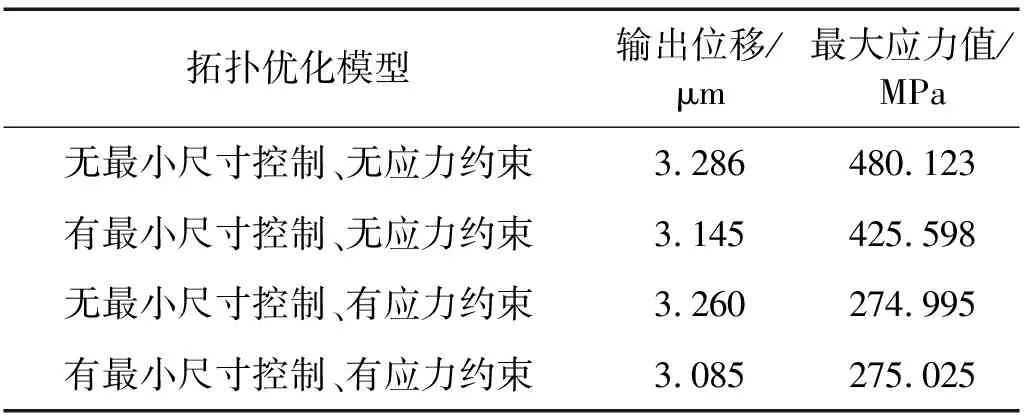
表1 不同優化模型的反向器拓撲優化結果

圖7 有最小尺寸控制、有應力約束的反向器拓撲優化Fig.7 Topological design of inverter mechanism with minimum length scale control and with stress constraints

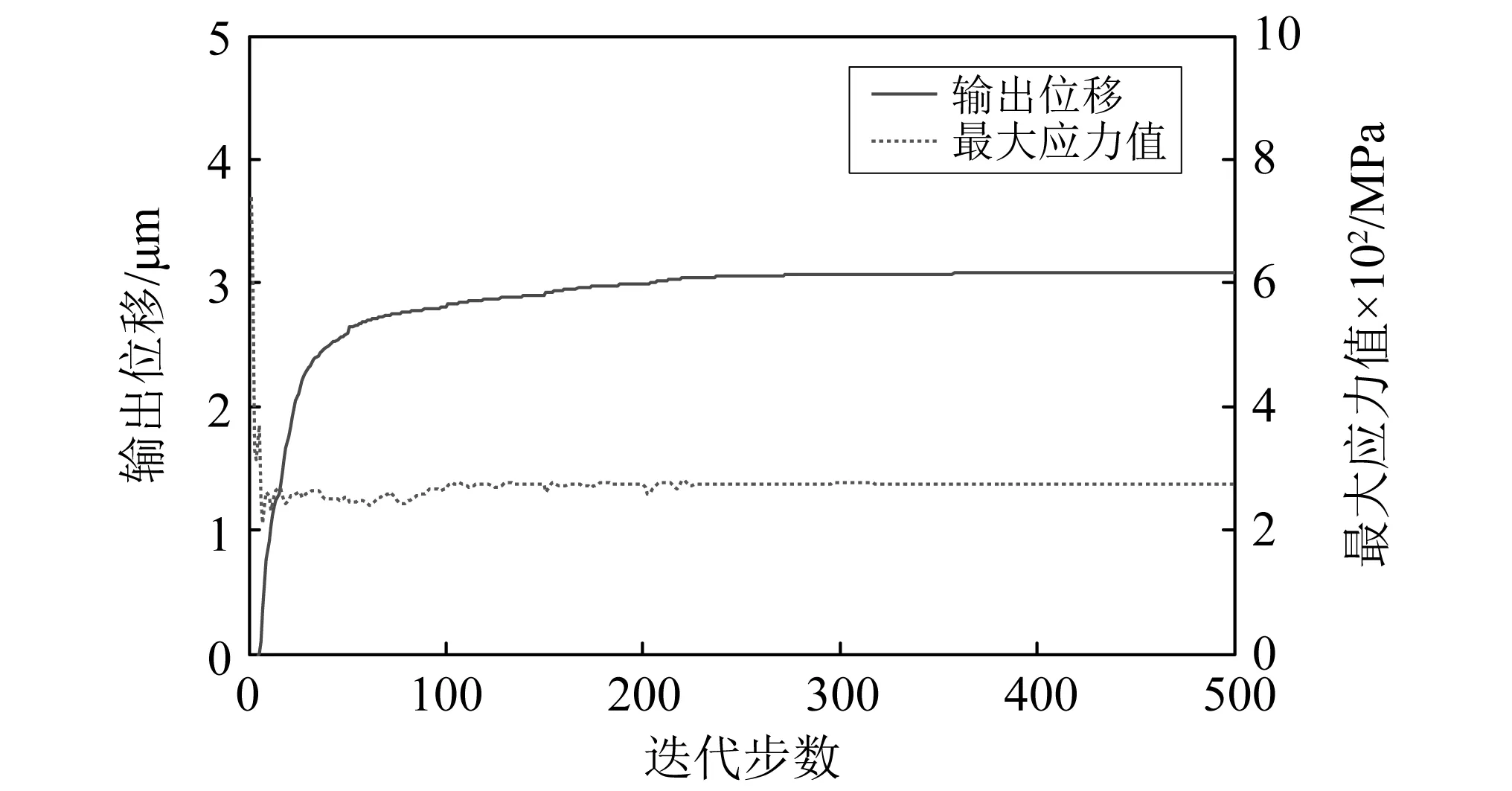
圖8 考慮混合約束的反向器拓撲優化迭代過程Fig.8 Iteration history for topology optimization of inverter mechanism with hybrid constraints

3.2 柔性咬合機構

圖9表示柔性咬合機構的設計域、固定邊界、輸入作用載荷以及輸出位移方向。設計域尺寸L×L為120 μm×120 μm，左上端和左下端為固定邊界，作用載荷F的大小為1.2×103μN，施加在右上端和右下端，左端中點為輸出端。輸入端剛度系數Kin和輸出端剛度系數Kout分別為2.5×103N/m和1.5×102N/m，允許的體積份數f*=0.20。同樣，由于咬合機構結構具有對稱性，取其一半進行設計，將設計域離散成120×60個四節點單元。

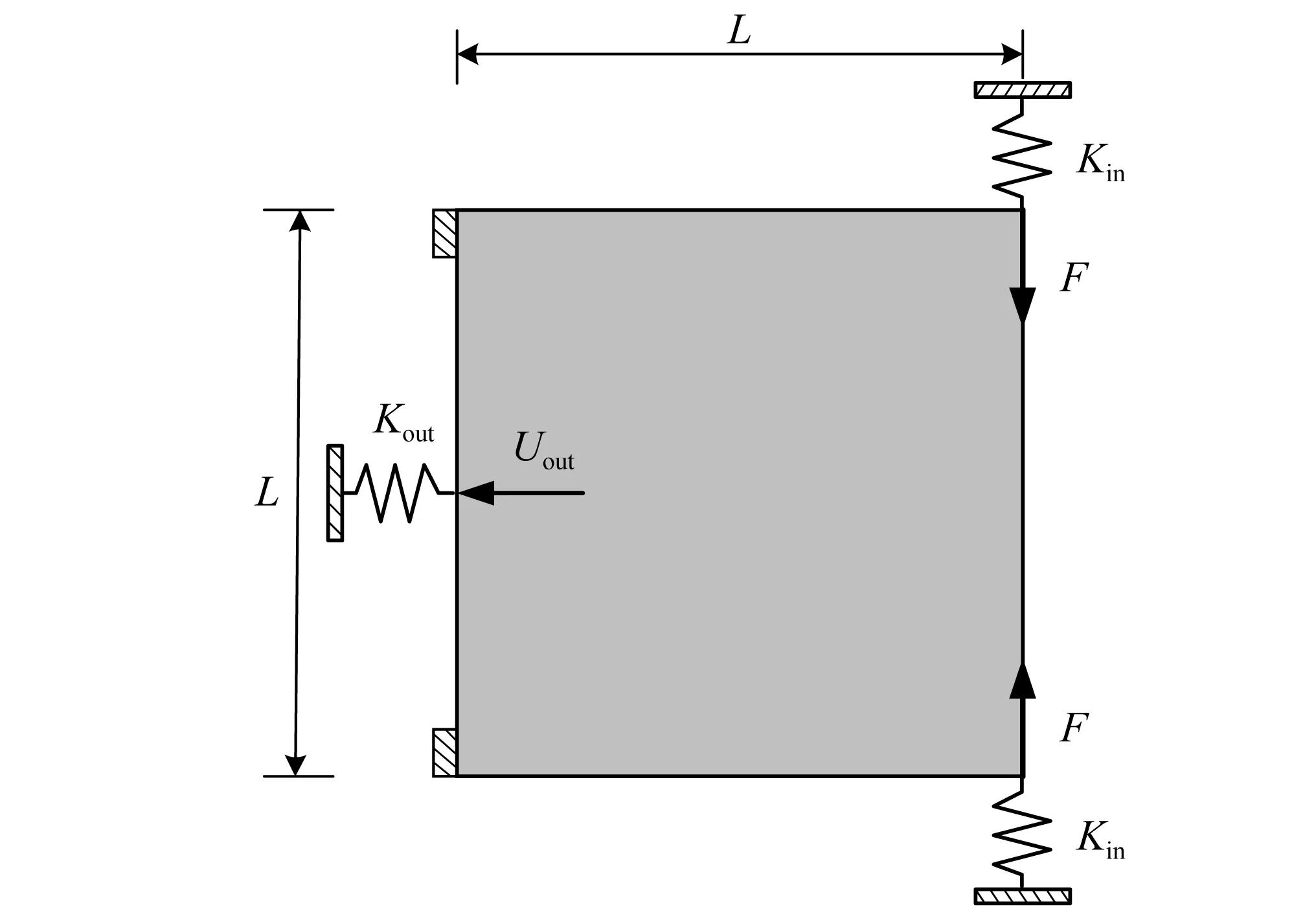
圖9 咬合機構設計域Fig.9 Design domain for crunching mechanism

圖10 無最小尺寸控制、無應力約束的咬合機構拓撲優化Fig.10 Topological design of crunching mechanism without minimum length scale control and without stress constraints

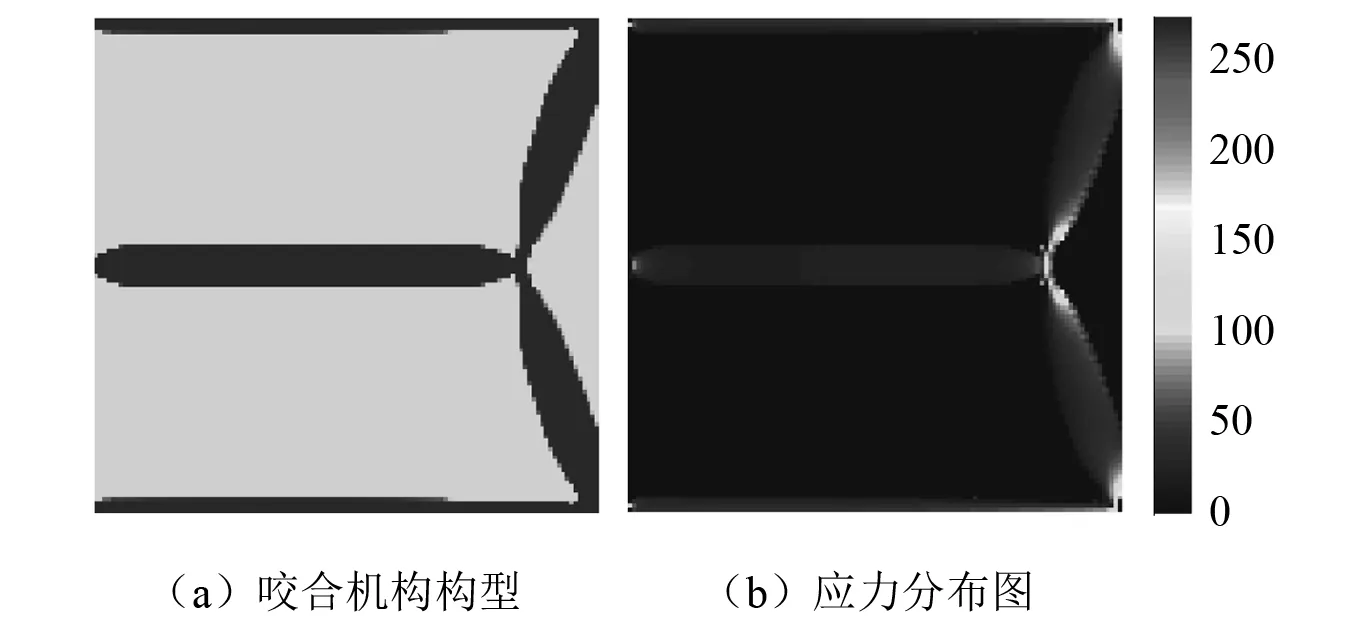
圖12 無最小尺寸控制、有應力約束的咬合機構拓撲優化Fig.12 Topological design of crunching mechanism without minimum length scale control and with stress constraints

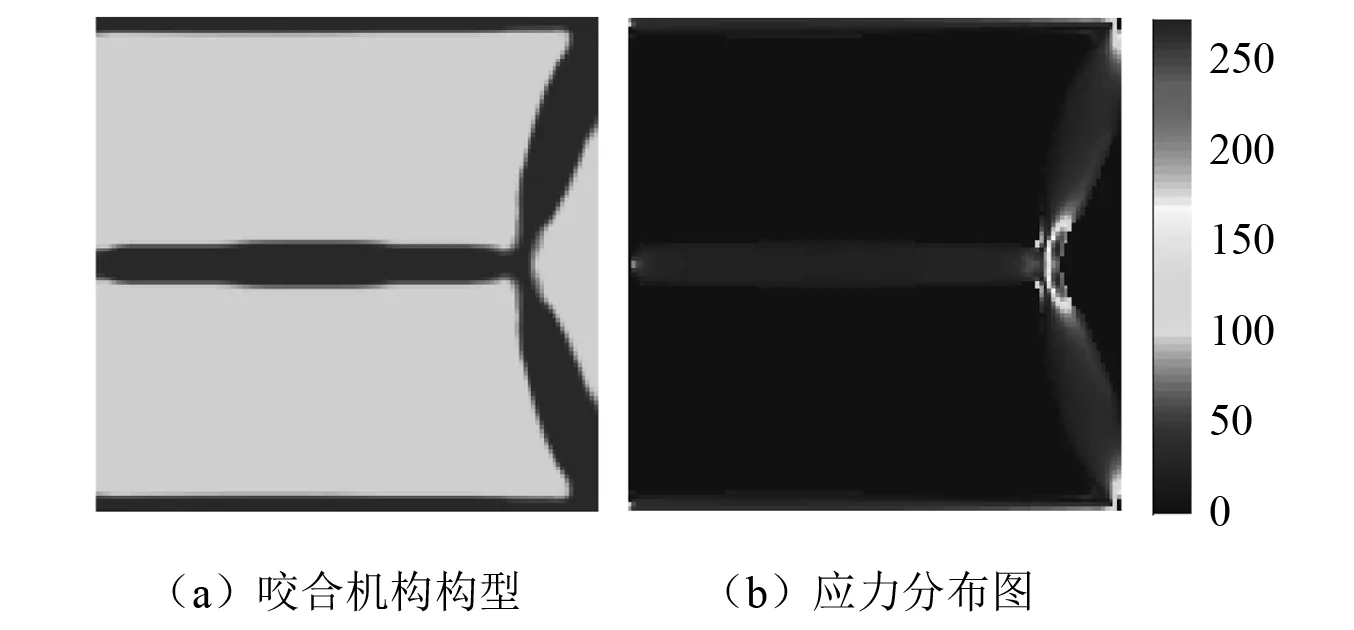
圖13 有最小尺寸控制、有應力約束的咬合機構拓撲優化Fig.13 Topological design of crunching mechanism with minimum length scale control and with stress constraints

混合約束拓撲優化獲得的咬合機構構型的實相和空相材料結構能夠滿足最小尺寸要求，有利于加工制造；最大值的應力為274.961 MPa，能夠很好地滿足應力約束，結構的應力分布相對均勻，因此機構構型能夠同時滿足最小尺寸制造約束和靜強度要求。由表2可知，與其他的三種拓撲優化模型優化結果相比，混合約束拓撲優化獲得的柔性咬合機構的輸出位移最小，由于混合約束在一定程度上限制了輸出位移的最大化。咬合機構混合約束拓撲優化設計迭代過程中，同樣初始階段會出現應力約束違反現象，造成一些波動，總體迭代過程平穩，如圖14所示。

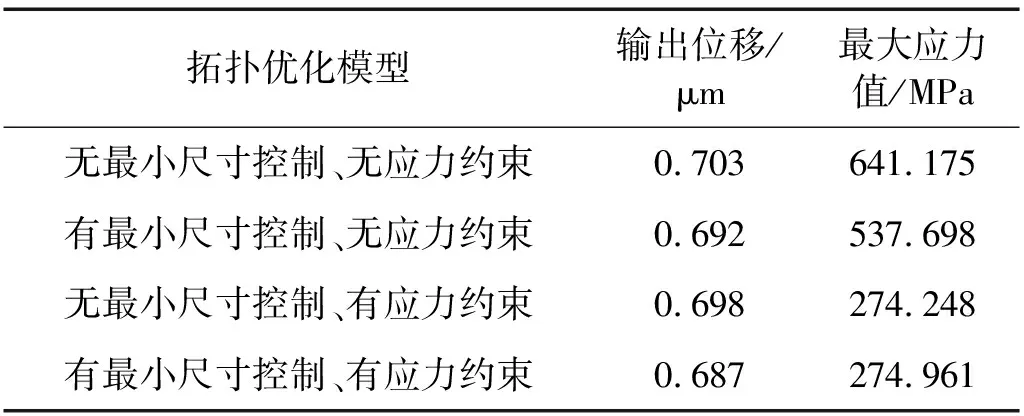
表2 不同優化模型的咬合機構拓撲優化結果

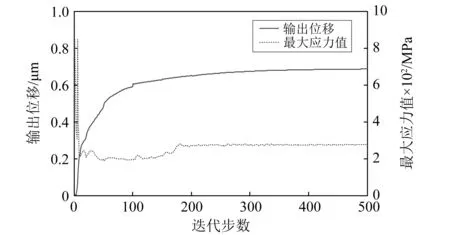
圖14 考慮混合約束的咬合機構拓撲優化迭代過程Fig.14 Iteration history for topology optimization of crunching mechanism with hybrid constraints

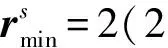
圖15 咬合機構混合約束拓撲優化設計Fig.15 Topological design of crunching mechanism with hybrid

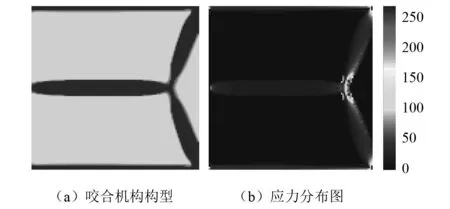
圖16 咬合機構混合約束拓撲優化設計Fig.16 Topological design of crunching mechanism with hybrid

4 結 論

(1)采用多相映射方法控制實體相和空洞相材料結構的最小尺寸，將P范數對所有單元局部應力約束進行最大近似處理，轉化為全局的應力約束，實現了綜合考慮最小尺寸空和應力約束的柔順機構混合約束拓撲優化設計。

(2)比較無應力約束條件下的有、無最小尺寸控制拓撲優化結果，最小尺寸控制拓撲優化獲得的柔順機構構型的實相和空相材料結構能夠滿足最小尺寸要求，并且可以在一定程度減少機構結構的應力水平。

(3)比較無最小尺寸控制條件下的有、無應力約束拓撲優化結果，有應力約束拓撲優化獲得的柔順機構構型的最小特征尺寸有所變大，但最小尺寸仍然過小，不易加工制造；能夠滿足靜強度要求。

(4)與其他的三種拓撲優化模型優化結果相比，混合約束拓撲優化獲得的柔順機構能夠同時滿足最小尺寸制造約束和靜強度要求，機構的von Mises等效應力分布更加均勻，但是混合約束使柔順機構的輸出位移有所減小。