顆粒形狀對堆石料力學特性影響的離散元分析

王蘊嘉，宋二祥，張千里

(1. 中國鐵道科學研究院集團有限公司鐵道建筑研究所，北京 100081；2. 清華大學土木工程系，北京 100084)

堆石料廣泛應用于土石壩、機場高填方路基和鐵路公路填方路基等填筑工程中[1-2]。堆石料取材便利、來源廣泛，不同工程中采用的堆石料在顆粒強度、顆粒形狀等方面存在較大差異。大量工程經驗表明，顆粒形狀是影響堆石料力學性能的重要因素之一，值得進行深入研究。

近年來，很多學者采用室內試驗方法研究顆粒形狀對堆石料、砂等散粒體材料力學特性的影響[3-13]。Chuhan 等[3]對砂土進行側限壓縮試驗，結果表明砂顆粒棱角越鮮明、越易發生破碎，材料的屈服應力越低。Varadarajan 等[4]分別對砂卵石堆石料和爆破堆石料進行相似級配試驗，發現二者表現出相反的試驗規律，進而認為顆粒形狀對材料破碎程度有較大影響。Afshar 等[5]采用電鏡掃描的方式統計了大量巖石顆粒的形狀特征并對其進行單顆粒壓碎試驗，發現顆粒球度越高越難破碎。鄒德高等[6]對單一粒組堆石料進行三軸試驗，研究顆粒顆粒形狀對顆粒破碎率的影響，發現堆石料顆粒破碎率隨顆粒球度的增加而減小。劉鋼等[7]對大量碎石顆粒進行統計分析，提出了顆粒幾何尺寸的量化表征參數，認為顆粒棱角與紋理是影響堆石料孔隙率的重要因素。Lashkari等[8]對六種不同形狀的砂進行直剪試驗，分析了顆粒形狀對試樣臨界狀態的影響，發現形狀越不規則，臨界狀態摩擦角越高。此外，田繼榮等學者[9-12]也進行了大量試驗研究，分析顆粒形狀對散粒體力學特性的影響。現階段室內試驗測得的大多是材料宏觀力學表現，難以捕捉顆粒細觀表現，不利于進行細觀機理分析，且天然材料形狀不規則難以控制單一變量，定量研究較困難。

堆石料是典型的顆粒材料，越來越多的學者采用多尺度分析方法研究其宏、細觀力學特性[13-14]。離散單元法由Cundall 和Strac[15]提出，該方法將介質視為一系列離散的獨立運動單元，可方便的處理非連續介質力學問題，常被用于研究顆粒形狀對散粒材料力學特性影響及其細觀機理[16-24]。Ng[16]對長短軸比值不同的橢球顆粒試樣進行三軸剪切試驗模擬，發現橢球顆粒長短軸之比越大、材料抗剪強度越小。邊學成等[17]采用自行開發的三維塊體離散元程序建立道砟顆粒模型，模擬分析道砟顆粒料在直剪試驗中的細觀力學特性。王蘊嘉和宋二祥[18]采用PFC3D 模擬研究球度對砂卵石堆積特性及強度的影響，并分析其細觀機理。Xu 等[19]采用三維離散元模擬分析顆粒形狀對試樣力學特性的影響，發現顆粒形狀越不規則，材料剪切強度越大，且顆粒形狀對臨界狀態線的影響不可忽略。Katagiri 等學者[20-24]也分別就考慮顆粒形狀的數值模型構造和形狀影響機理開展研究。

與一般土體相比，堆石料粒徑大、顆粒破碎明顯，研究中應考慮顆粒破碎的影響[25]。基于此，常曉林等[26]采用SGDD 模型，分析顆粒形狀及粒間摩擦角的影響，并建立粒間摩擦角與非線性強度參數的對應關系。Zhou 等[27-28]采用FEM與DEM 相結合的模擬方法研究顆粒形狀的影響，結果表明顆粒形狀越狹長、顆粒破碎越顯著。Wang 等[29]模擬分析了顆粒形狀對堆石料蠕變特性的影響，發現堆石料顆粒棱角越尖銳、蠕變速率越大。Zhang 等[30]對不同顆粒形狀試樣進行模擬試驗，發現不規則顆粒試樣會產生更多的破碎，且顆粒破碎與能量輸入的關系受顆粒形狀影響。可破碎材料的力學性能與顆粒強度密切相關，目前對綜合考慮顆粒形狀和顆粒強度影響的研究尚不充分，且尚未建立顆粒形狀參量與試樣宏觀力學性能參數的對應關系。

本文以爆破堆石料為研究對象，采用離散元軟件PFC3D 根據真實顆粒形狀建立不同球度的單顆粒模型，分別生成不破碎和可破碎試樣并進行三軸剪切試驗模擬，分析顆粒球度對堆石料力學特性的影響及細觀機理。

1 數值模型及試驗方案

1.1 單顆粒模型

Barrett[31]對已有的巖石顆粒形狀相關研究進行綜述，提出顆粒形狀一般可從宏觀、中觀、細觀三個尺度來描述。宏觀尺度一般指顆粒的整體形狀，例如正方形或三角形；中觀尺度指顆粒局部變化的劇烈程度，例如角部圓滑或尖銳；細觀尺度是指顆粒表面形態，例如光滑或粗糙。本文暫不考慮堆石料顆粒的中觀、細觀形態，僅從宏觀尺度出發討論顆粒形狀對堆石料力學特性的影響。參考文獻[18]，采用球度S作為描述顆粒宏觀形態的計算參數。

爆破堆石料由于爆破開采的原因，顆粒往往棱角分明，這使其在受力過程中應力集中更明顯，顆粒破碎現象十分顯著。對于爆破堆石料而言，顆粒破碎是影響材料力學特性的重要因素，模擬時需考慮顆粒破碎。基于此，采用可模擬顆粒破碎的顆粒簇單元來構建單顆粒模型。

如圖1 所示，依據真實顆粒形狀建立不同球度S的爆破堆石料單顆粒模型。單顆粒模型由半徑相同的球顆粒粘結而成，球顆粒按密排六方結構排列。綜合考慮單顆粒模型的精細程度和計算效率，分別采用13 顆粒、23 顆粒和33 顆粒的顆粒簇作為球度分別為0.878、0.617 和0.446 的單顆粒模型，不同模型的圓度及表面粗糙度均相同。

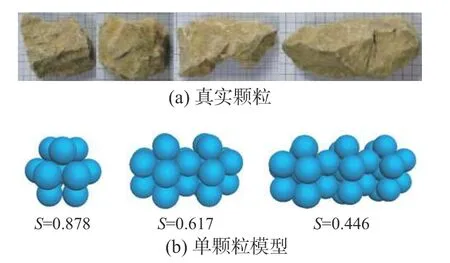
圖1 真實顆粒與單顆粒模型Fig. 1 Rocks and particle model

單顆粒模型內的球顆粒互相不重疊，顆粒真實密度即為計算密度，無需修正。球顆粒之間采用平行粘結模型，當接觸所受的拉應力或剪應力超出平行粘結的法向或切向強度時，粘結破壞，此后接觸仍采用線性接觸模型和滑移模型來模擬。模型的顆粒力學參數如表1 所示。

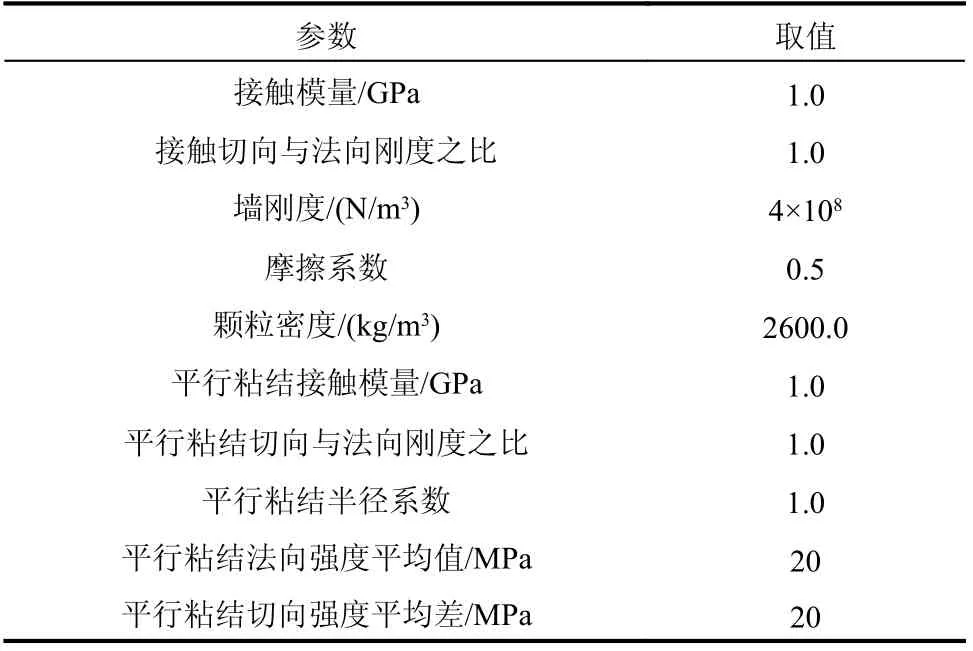
表1 顆粒力學參數Table 1 Granular mechanical parameters

1.2 單元試驗模型

顆粒流模擬試驗中，數值試樣尺寸過小可能會導致結果不可靠[32]。參考已有研究，綜合考慮計算結果可靠性和計算效率，試樣邊長與顆粒平均直徑之比在5～9，最大與最小顆粒粒徑之比為1.25。數值試樣及試樣尺寸參數分別如圖2 和表2所示。采用文獻[18]提出的制樣方法進行制樣，制樣摩擦系數取0.1，試樣相對密實度為0.75。

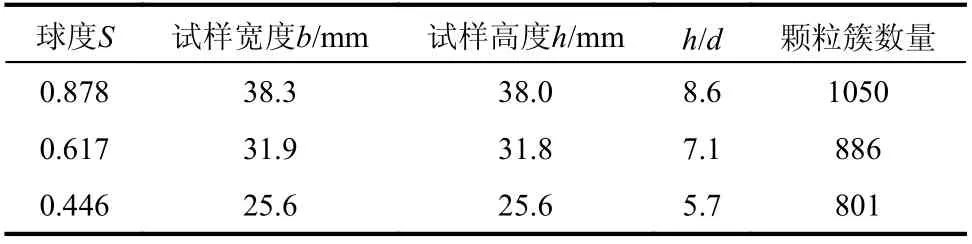
表2 數值試樣參數Table 2 Parameters of numerical models

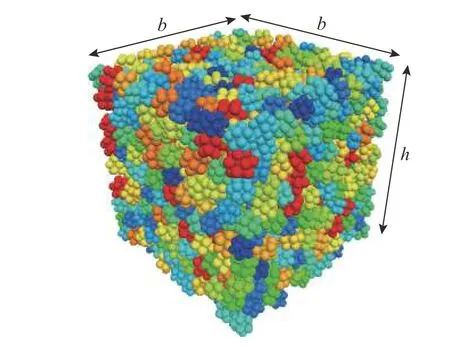
圖2 數值試樣(S=0.878)Fig. 2 Numerical sample (S=0.878)

1.3 試驗方案

為討論顆粒破碎的影響，分別生成不破碎爆破料試樣和可破碎爆破料試樣。兩組試樣的接觸剛度、摩擦系數等顆粒力學參數均相同，僅粘結強度不同。不破碎試樣用于模擬顆粒強度較高的情況，可認為材料在常用應力水平范圍內幾乎不發生破碎，顆粒破碎的影響可忽略不計，此時粘結強度均值取2000 MPa；可破碎試樣用于模擬材料強度較低的情況，顆粒破碎顯著，其影響不可忽略，此時粘結強度按照表1 取值。

分別對兩組試樣進行三軸剪切試驗模擬，圍壓取值為400 kPa、600 kPa、800 kPa 和1000 kPa。顆粒球度取值分別為0.878、0.617 和0.446。

2 模擬結果及分析

2.1 三軸剪切試驗結果

2.1.1 應力-應變曲線

圖3 和圖4 為不同圍壓、不同球度時不破碎試樣的應力-應變曲線。由圖3 可知，當試樣顆粒形狀不變時，偏應力隨圍壓增大而增大，試樣剪脹性隨圍壓增大而減小，這與已有的試驗結果[2]是一致的。由圖4 可知，圍壓為800 kPa 時，峰值偏應力及殘余偏應力均隨S的減小而增大，試樣剪脹性隨S的減小而減小。這與已有模擬研究[26]得到的規律相符。

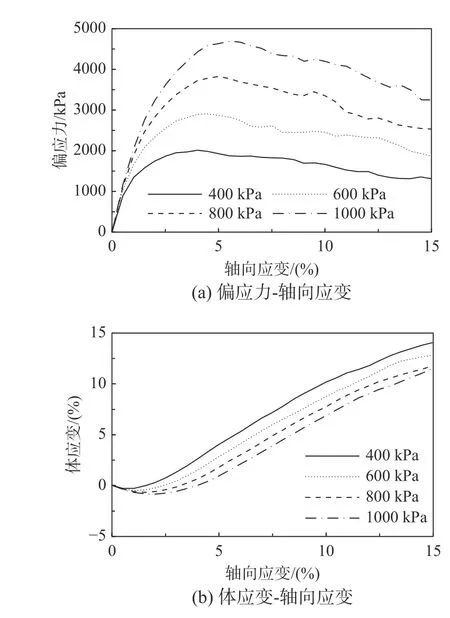
圖3 圍壓對不破碎試樣三軸剪切試驗表現的影響(S=0.878)Fig. 3 The effect of confining pressure on triaxial compression behavior of unbreakable specimens (S=0.878)

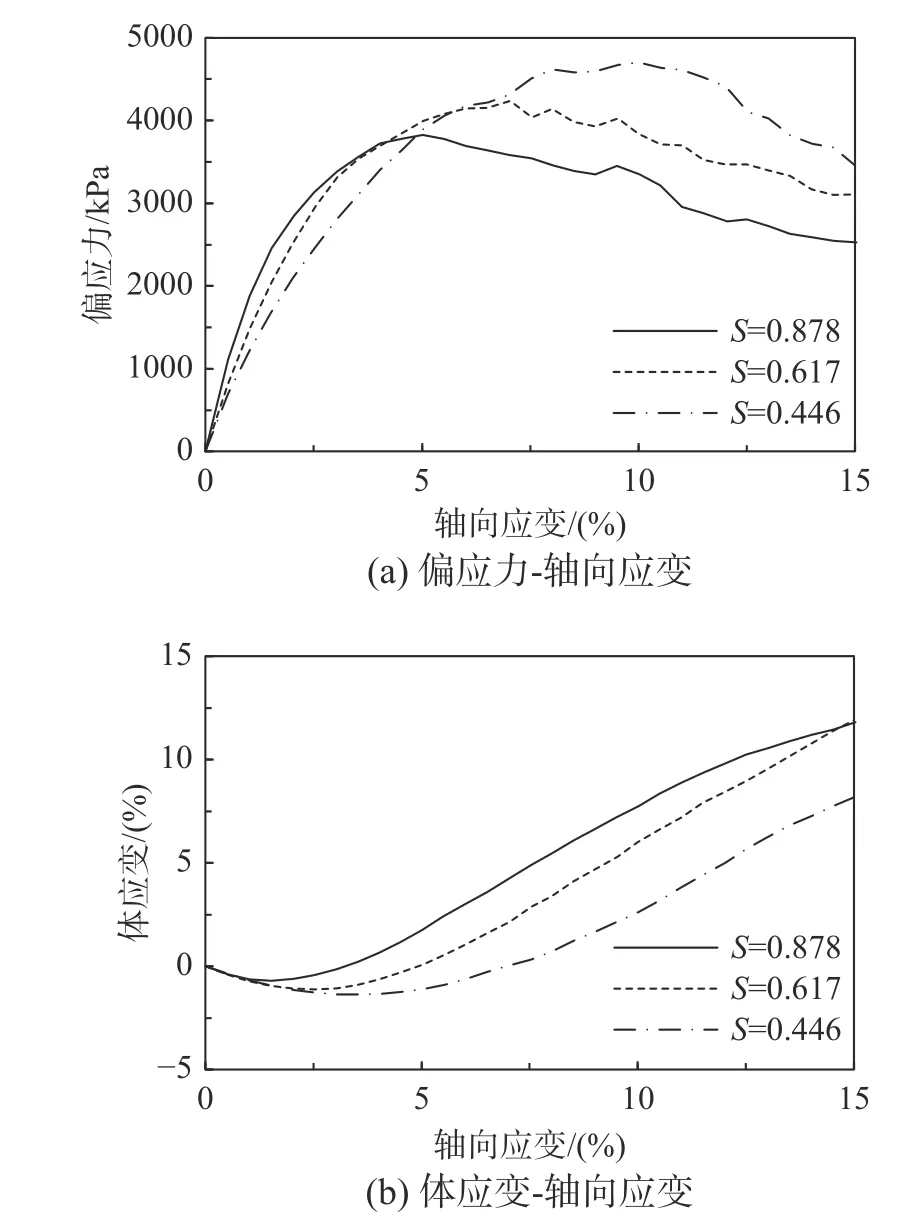
圖4 球度對不破碎試樣三軸剪切試驗表現的影響(800 kPa)Fig. 4 The effect of S on triaxial compression behavior of unbreakable specimens (800 kPa)

圖5 和圖6 為不同圍壓、不同球度時可破碎試樣的應力-應變曲線。由圖可知，圍壓為400 kPa時，峰值偏應力受球度影響較小，試樣剪脹性隨S的減小而減小；圍壓增加至800 kPa 時，峰值摩擦角隨S的減小而減小，試樣剪脹性隨S減小而減小，峰值摩擦角變化規律與400 kPa 圍壓時并不相同。

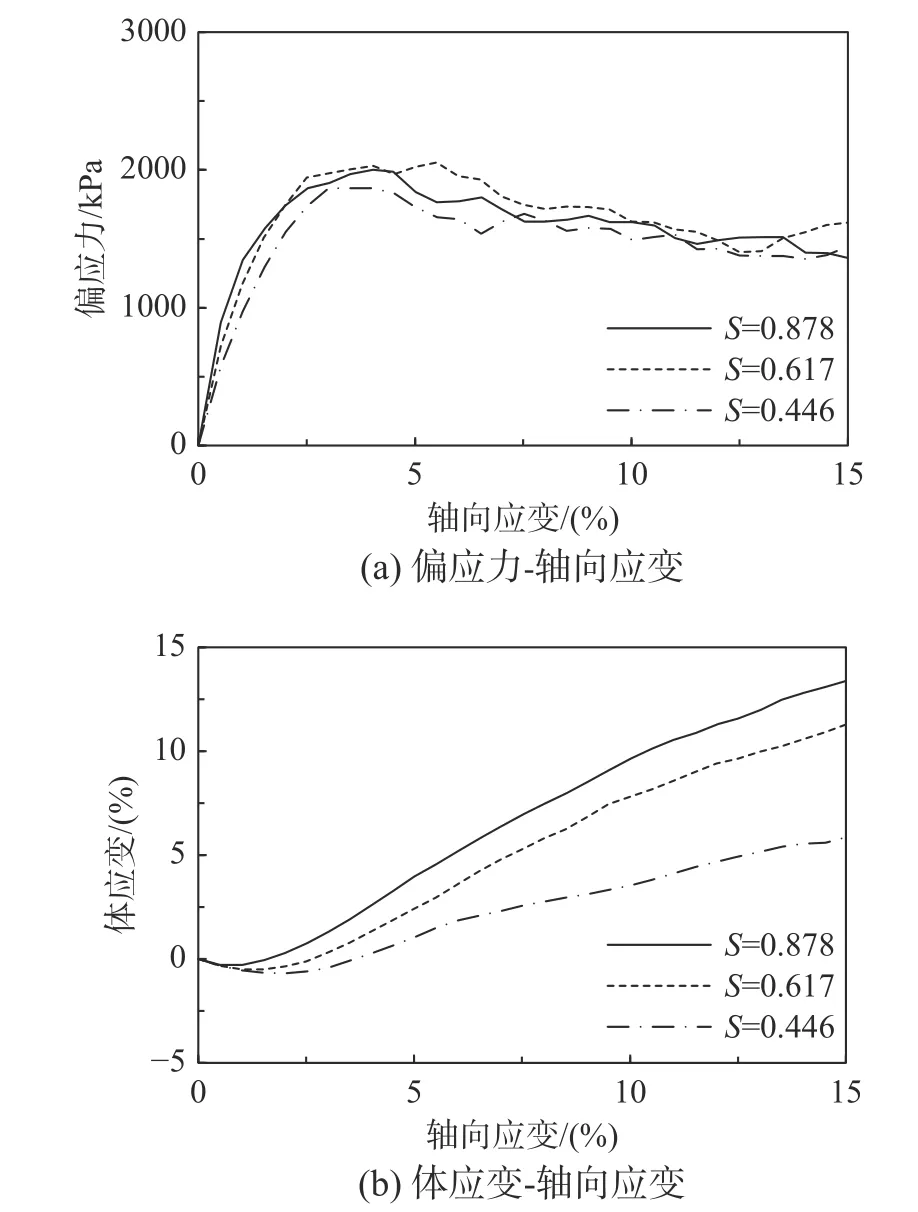
圖5 球度對可破碎試樣三軸剪切試驗表現的影響(400 kPa)Fig. 5 The effect of S on triaxial compression behavior of breakable specimens (400 kPa)

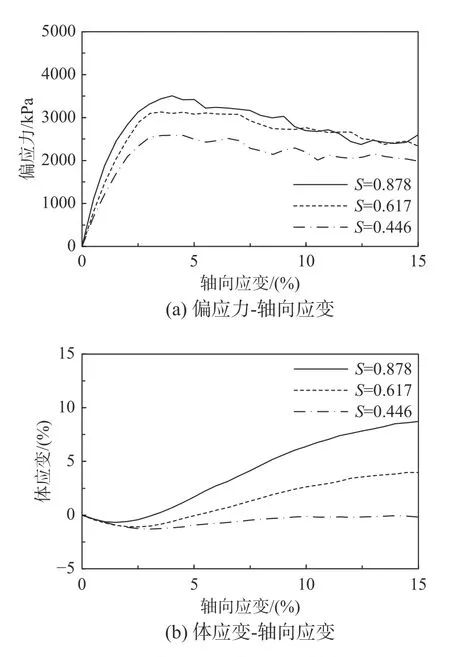
圖6 球度對可破碎試樣三軸剪切試驗表現的影響(800 kPa)Fig. 6 The effect of S on triaxial compression behavior of breakable specimens (800 kPa)

對比不破碎試樣和可破碎試樣的三軸剪切試驗結果可知，顆粒球度對試樣強度的影響規律與顆粒破碎即顆粒強度有關，顆粒強度高、圍壓低時，試樣強度隨S的增大而減小，顆粒強度低、圍壓高時，試樣強度隨S的增大而增大；試樣剪脹性均隨S的增大而增大，且圍壓和S均相同時，可破碎試樣剪脹性小于不破碎試樣。

2.1.2 峰值摩擦角

圖7 分別為不破碎和可破碎試樣的峰值摩擦角。由圖可知，不考慮顆粒破碎時(顆粒強度高)，試樣峰值摩擦角隨圍壓增大稍有降低，隨S增大而減小；考慮顆粒破碎時(顆粒強度低)，峰值摩擦角隨圍壓增大而迅速減小，且S越小峰值摩擦角減小的程度越大。

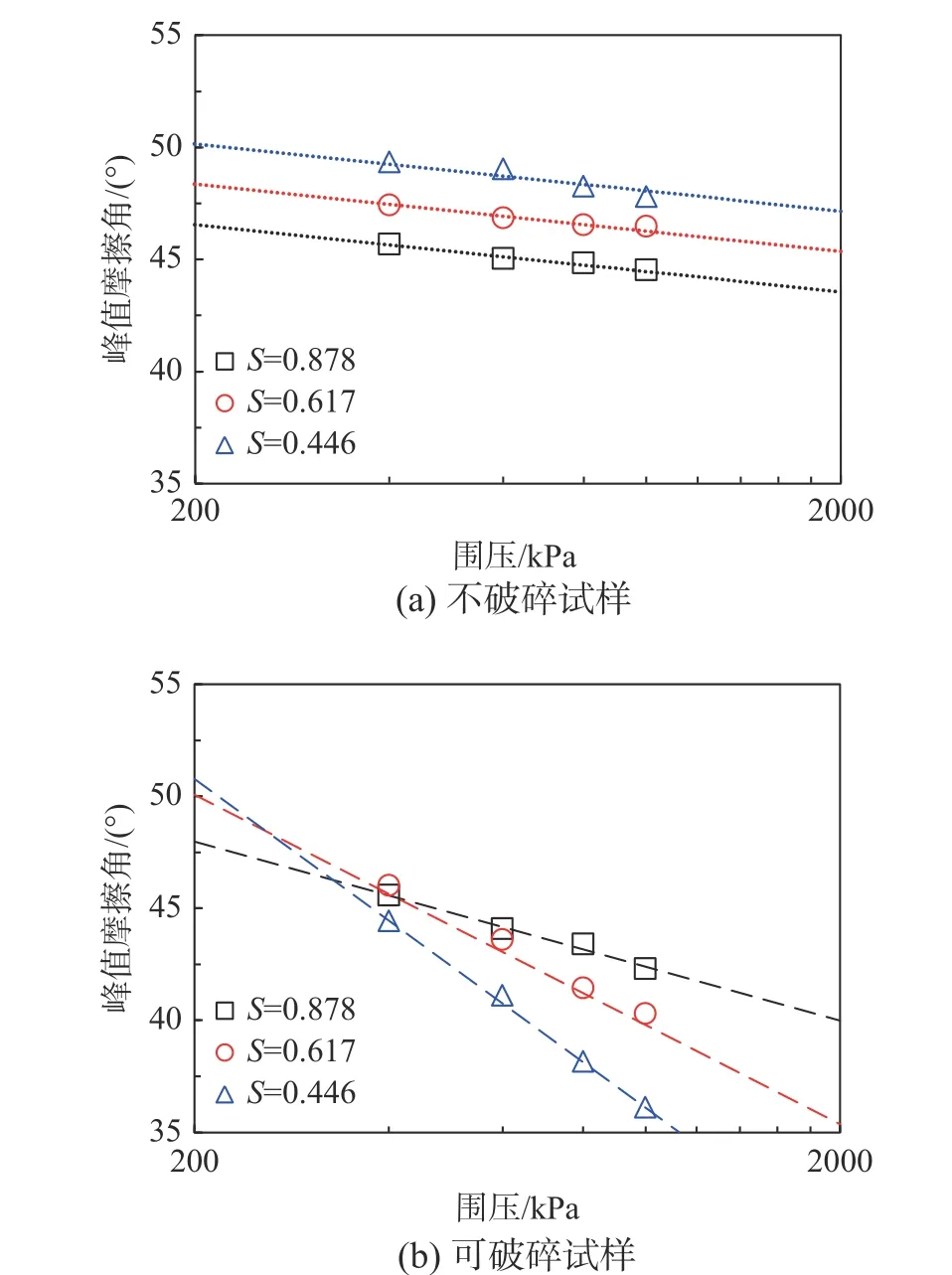
圖7 峰值摩擦角Fig. 7 Peak friction angle

粗粒料峰值摩擦角由兩部分組成：一是顆粒間滑動時的滑動摩擦角；二是顆粒間由于咬合產生的咬合摩擦，也可理解為剪脹角。不考慮顆粒破碎時，剪脹角隨圍壓增大而稍有降低(圖7(a))；考慮顆粒破碎時，圍壓增大，顆粒破碎量增加，咬合摩擦即剪脹角顯著減小，使得峰值摩擦角隨圍壓增大而顯著減小(圖7(b))。

S的影響可從以下兩方面分析：首先，S越小顆粒不規則程度越高，試樣內顆粒咬合、內鎖程度越高，會提高試樣強度；其次，S越小越容易發生顆粒破碎，尤其是平均壓應力水平高時，這會降低試樣強度。試樣強度的提高或降低取決于兩種作用疊加后的效果，因此，在討論顆粒形狀影響時，需綜合考慮顆粒破碎的影響。基于以上分析，S對堆石料強度的影響可依據平均壓應力水平的不同大致分為三個區域：當平均壓應力水平低時，S的影響以增大試樣內顆粒咬合、內鎖為主，試樣強度隨S的減小而增大；當平均壓應力水平高時，S的影響以增加試樣內顆粒破碎為主，試樣強度隨S的減小而減小；當平均壓應力水平適中時，S減小時增大顆粒咬合和增加顆粒破碎的作用相當。

峰值摩擦角和圍壓在半對數坐標系內有較好的線性關系，圍壓越高，顆粒破碎越多，咬合摩擦越小。本文在Duncan 等[33]建議的非線性強度公式基礎上進行改進，提出可反映球度S影響的峰值摩擦角表達式：

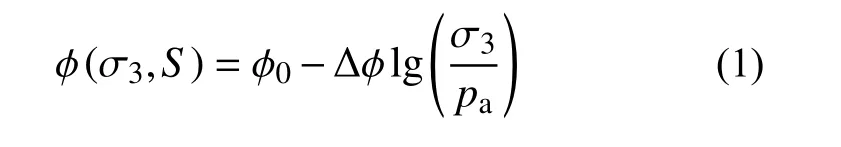
其中：

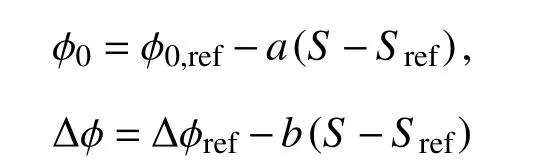
式中：pa用于平衡量綱，取值一個標準大氣壓；Sref為參考球度； φ0,ref和 Δφref為S=Sref時的 φ0和Δφ取值；a和b為反映球度影響的擬合參數。

本算例中，取Sref=0.878 ，不同球度時 φ0和Δφ取值如圖8 所示，此時各參數取值如表3 所示。

表3 峰值摩擦角公式參數Table 3 Parameters of the peak friction angle formula

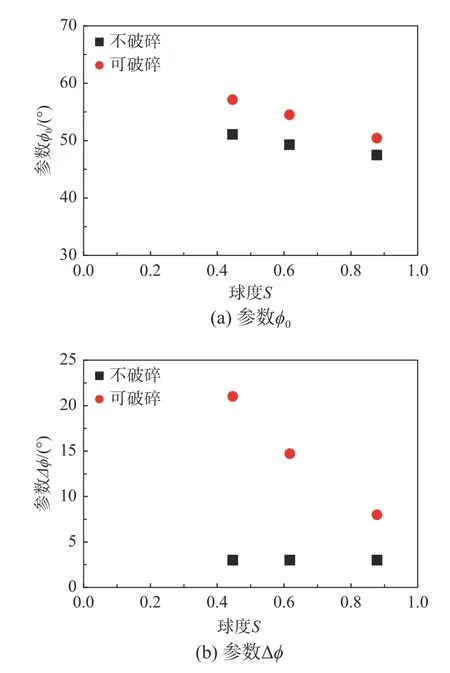
圖8 S 對峰值摩擦角公式參數的影響Fig. 8 The effect of S on parameters of the peak friction angle formula

需注意的是，半對數坐標系下，試樣峰值摩擦角隨圍壓增大而減小，近似線性關系，但減小的斜率絕對值并不是固定的，可大致分為兩階段：當圍壓低時，顆粒幾乎不破碎，峰值摩擦角-圍壓曲線的斜率絕對值較小；當圍壓高時，顆粒大量破碎，峰值摩擦角-圍壓曲線的斜率絕對值較大。因此，若只采用高圍壓時的峰值摩擦角擬合強度曲線，其曲線斜率絕對值較大，會高估低圍壓時的試樣強度。

2.1.3 初始彈性模量

圖9 為S對三軸剪切試驗中初始彈性模量E0的影響。由于剪切初始階段顆粒破碎較少，對初始彈性模量的影響可忽略不計，此處僅給出不破碎試樣的初始彈性模量。由圖可知，E0隨圍壓增大而增大，且隨S增大而增大。

圖9 初始彈性模量Fig. 9 Initial tangent modulus

根據計算結果對Janbu 公式[34]進行修正，提出可反映球度S影響的初始彈性模量表達式：

其中：

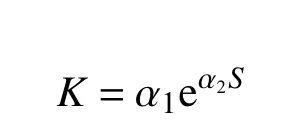
式中， α1、 α2和n為擬合參數。

對圖9 中數據進行擬合，K取值如圖10 所示，擬合參數取值如表4 所示。

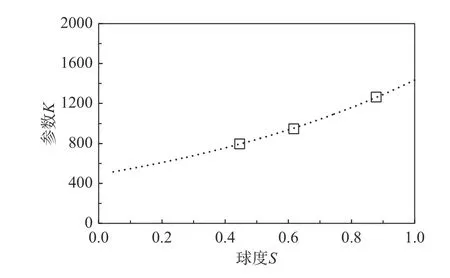
圖10 S 對參數K 的影響Fig. 10 The effect of S on K

表4 初始彈性模量公式參數Table 4 Parameters of the initial tangent modulus formula

2.2 細觀組構分析

顆粒材料的細觀組構是指顆粒在空間中的分布、定向，孔隙在空間中的分布，顆粒間的相互作用，以及這些因素在空間中的分布情況。細觀組構及其演化規律常用于解釋和預測顆粒材料的宏觀力學行為。本部分針對不破碎和可破碎試樣，采用不同的細觀組構進行分析。

2.2.1 不破碎試樣

采用接觸力平均值、拉應力平均值和接觸各向異性指標來描述和分析不破碎材料的細觀表現[13]。接觸力平均值是指試樣內所有顆粒間接觸的力的平均值，描述試樣內顆粒整體受力水平；拉應力平均值是指顆粒內所有接觸的拉應力的平均值，描述顆粒內拉應力水平；接觸各向異性指標 φ描述試樣內顆粒間接觸的各向異性程度，可采用下式計算：

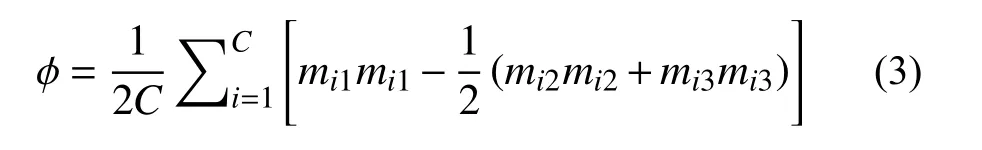
式中：C是試樣內顆粒間的接觸個數；mi1、mi2和mi3分別為第i個接觸法向向量的第一、第二和第三主分量。

圖11 為S=0.878 時不同圍壓下的接觸力平均值、拉應力平均值和接觸各向異性指標曲線。由圖11(a)和圖11(b)可知，接觸力平均值隨軸向應變的增加而逐漸增大，且當圍壓從400 kPa 增大至1000 kPa 時，相同軸向應變時接觸力平均值隨圍壓增大而增大；拉應力平均值變化規律與接觸力平均值基本相同。以上結果說明，圍壓越高，試樣內接觸力水平和顆粒內拉應力水平都越高。

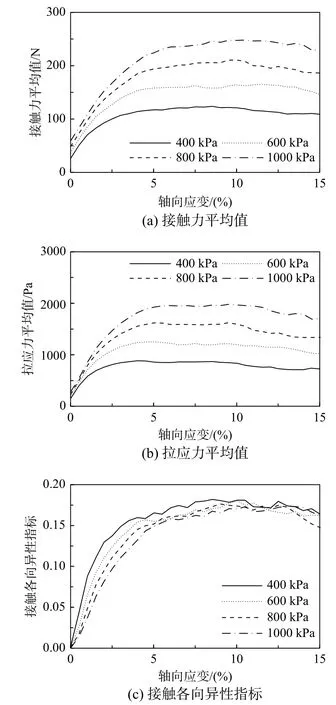
圖11 圍壓對細觀組構參量的影響(S=0.878)Fig. 11 The effect of confining pressure on meso-fabric parameters (S=0.878)

由圖11(c)可知，接觸各向異性指標隨軸向應變增大而增大并最終保持不變；圍壓越低，接觸各向異性指標隨軸向應變增加而增大的速率越快，這與圖3(a)中的應力應變曲線是相對應的，圍壓越低，試樣達到峰值強度時所需的軸向應變越小。

圖12 為圍壓800 kPa 時不同球度下的接觸力平均值、拉應力平均值和接觸各向異性指標曲線。由圖12(a)和圖12(b)可知，接觸力平均值和拉應力平均值均隨著軸向應變的增加而逐漸增大，且當軸向應變相同時，隨S減小而增大。以上結果說明，相同應力水平時，顆粒S越小、顆粒間接觸力和顆粒內拉應力越大，即顆粒越容易破碎。圖12(c)為接觸各向異性指標曲線，結合圖4(a)分析可知，剪切初期(軸向應變小于5%時)接觸各向異性指標增大速率與試樣達到峰值強度所需的軸向應變是相關的，球度越大，接觸各向異性指標增大速率越大，試樣達到峰值強度所需的軸向應變越小。

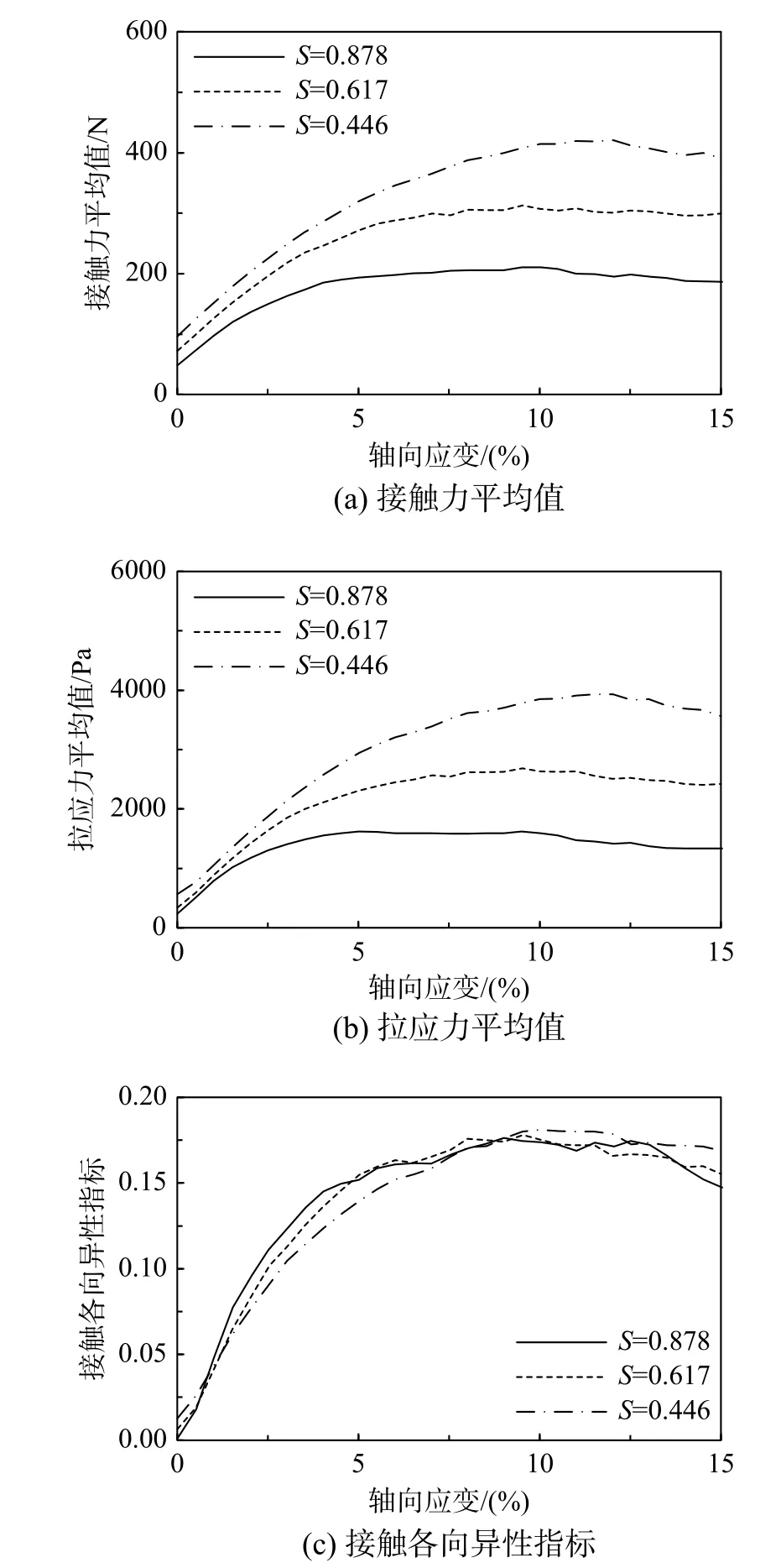
圖12 球度對細觀組構參量的影響(800 kPa)Fig. 12 The effect of S on meso-fabric parameters (800 kPa)

2.2.2 可破碎試樣

對于可破碎試樣，重點研究圍壓和球度對顆粒破碎的影響，采用相對破碎率表征試樣中顆粒破碎程度。相對破碎率Br由Hardin[35]提出，反映破碎前后試樣級配曲線的變化，可采用下式計算：

式中：Bt為試驗前后試樣破碎勢之差；Bp為試樣初始破碎勢。

圖13 為S=0.878 時不同圍壓下的相對破碎率曲線。由圖可知，相對破碎率曲線可分為兩階段描述，當軸向應變小于界限應變時相對破碎率為0，當軸向應變大于界限應變時，相對破碎率隨應變增大而增大；當軸向應變相同時，相對破碎率隨圍壓增大而增大。

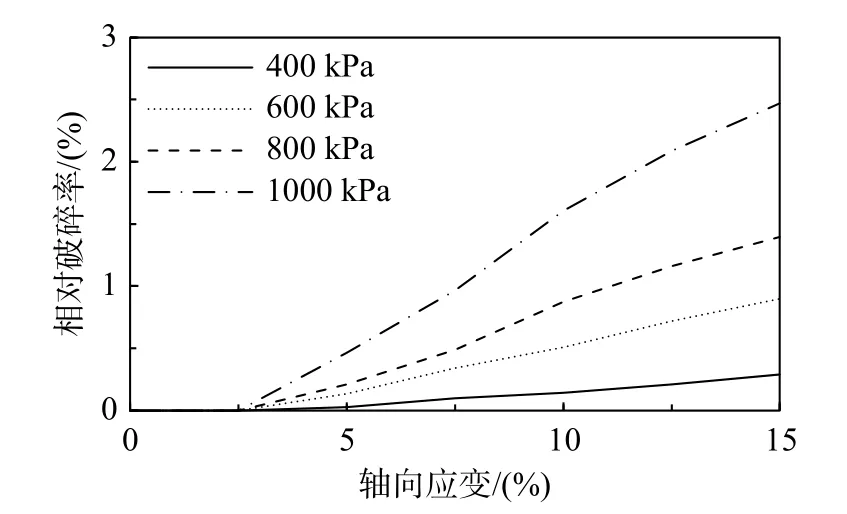
圖13 圍壓對相對破碎率的影響(S=0.878)Fig. 13 The effect of confining pressure on relative breakage rate (S=0.878)

圖14 為圍壓800 kPa 時不同球度的相對破碎率曲線。由圖可知，相對破碎率關系曲線同樣可分為二階段描述，當軸向應變小于界限應變時，顆粒幾乎不破碎，相對破碎率近似為0，當軸向應變大于界限應變時，相對破碎率隨應變增大而增大；當軸向應變相同時，相對破碎率隨S減小而增大。以上計算結果說明，顆粒球度越小，形狀越不規則，相同應力水平時越易破碎，這與2.2.1節分析結果是一致的。

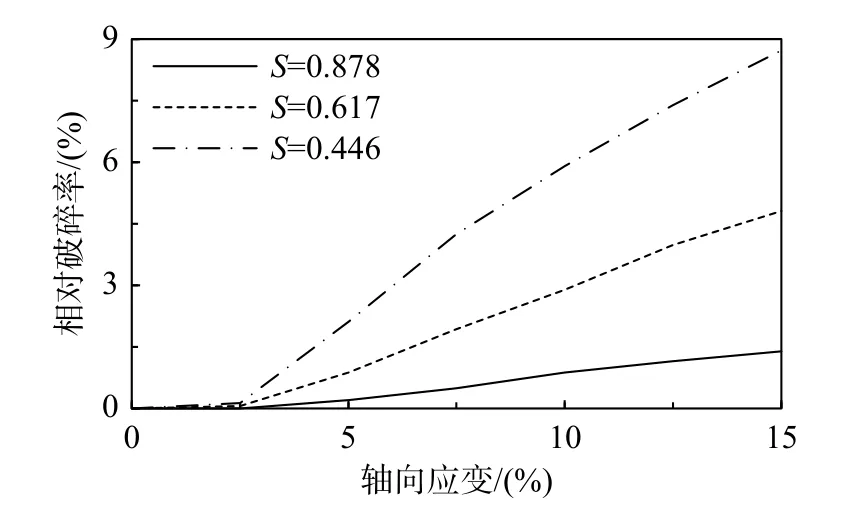
圖14 球度對相對破碎率的影響(800 kPa)Fig. 14 The effect of S on relative breakage rate (800 kPa)

圖15 是不同圍壓和球度的相對破碎率。由圖可知，S相同時，相對破碎率隨圍壓增大而增加，近似線性關系；圍壓相同時，相對破碎率隨S增大而減小，近似成半對數線性關系。分析表明，圍壓越大，S越小，顆粒破碎越多，相對破碎率越大，這與鄒德高等[6]的試驗結果是一致的，也與2.1.2 節峰值摩擦角計算結果相吻合。

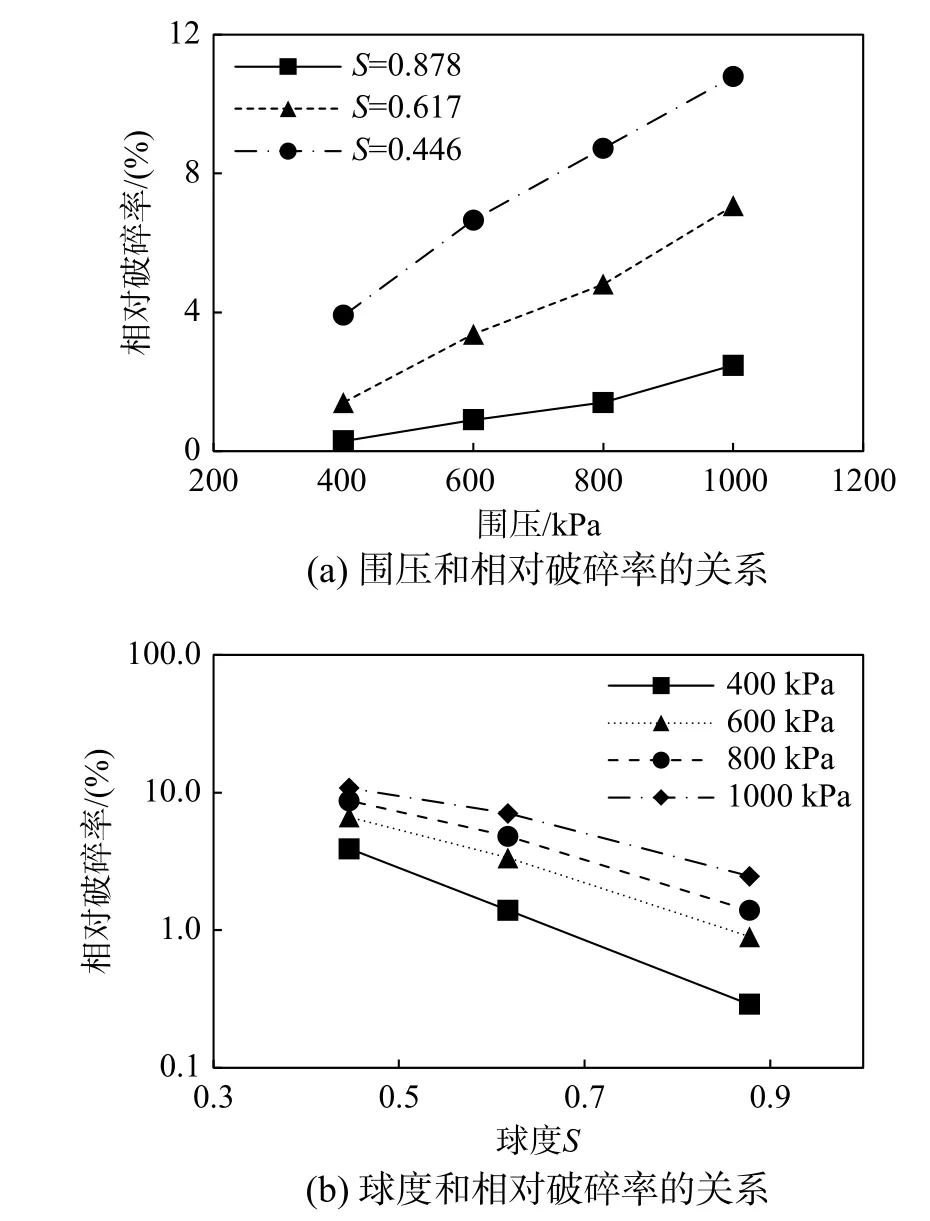
圖15 圍壓和球度對相對破碎率的影響Fig. 15 The effect of confining pressure and S on relative breakage rate

計算不破碎試樣與破碎試樣的峰值摩擦角差值，并將其與相對破碎率對應，如圖16 所示。由圖可知，二者近似線性關系，即顆粒破碎越顯著，峰值摩擦角差值越大，且基本不受球度的影響。

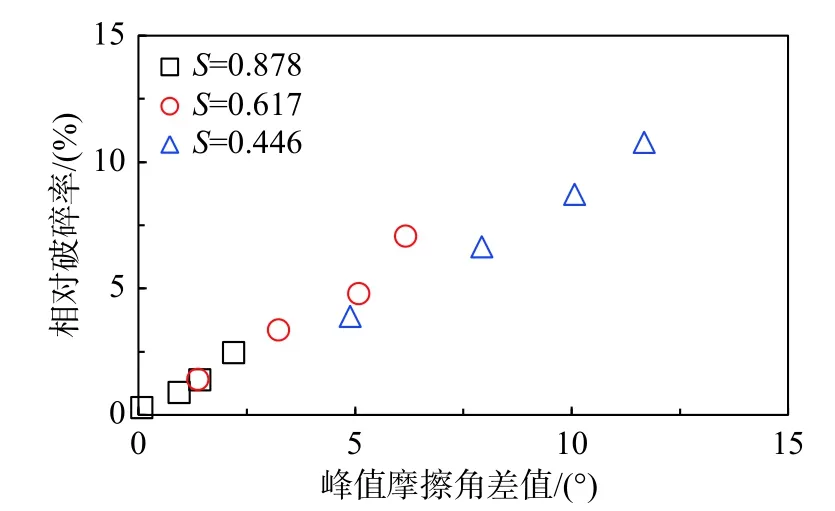
圖16 相對破碎率和峰值摩擦角差值的關系Fig. 16 Relation between relative breakage rate and difference of peak friction angle

3 結論

本文以爆破堆石料為研究對象，采用顆粒流軟件PFC3D 模擬分析了顆粒球度對堆石料力學特性的影響及其細觀機制，得到以下結論：

(1) 堆石料峰值摩擦角同時受顆粒強度、圍壓以及顆粒球度的影響。顆粒強度高、圍壓低時，峰值摩擦角隨球度增大而減小；顆粒強度低、圍壓高時，峰值摩擦角隨球度增大而增大。

(2) 顆粒球度對堆石料強度影響體現在顆粒咬合和顆粒破碎兩方面。顆粒球度越小、形狀越不規則，顆粒間咬合、內鎖程度越高，增大試樣強度；而顆粒球度越小，顆粒內拉應力水平越高、顆粒破碎越多，降低試樣強度。顆粒球度對堆石料強度的影響是二者綜合作用的結果。

(3) 堆石料初始彈性模量受顆粒破碎影響較小，隨圍壓與增大而增大，隨顆粒球度的增大而增大，但與顆粒是否破碎關系不大。