基于生成對抗與卷積神經網絡的調制識別方法

邵 凱, 朱苗苗, 王光宇

(1. 重慶郵電大學通信與信息工程學院, 重慶 400065; 2. 移動通信教育部工程研究中心,重慶 400065; 3. 移動通信技術重慶市重點實驗室, 重慶 400065)

0 引 言

自動調制識別是指自動識別接收信號的調制類型,是頻譜監測、信息對抗、認知無線電等各種應用中的一項重要技術。隨著無線通信技術的日益發展,信號的調制趨于多樣化,電磁環境也越來越復雜。對實時高效的調制識別技術的研究,具有重大的現實意義。

目前調制識別的研究方法主要可以分為兩類:一是基于似然比(likelihood based,LB)的調制識別,二是基于特征(feature based,FB)的調制識別。LB方法是通過對似然函數進行處理,將得到的似然比與閾值進行比較,從而對調制信號進行分類。盡管LB方法在貝葉斯意義上可得到最優解,但需要參數估計或有關信道知識的假設。當未知參數較多時,識別準確率會嚴重下降;當調制信號的類型較多時,LB方法的計算復雜度會升高。相比之下FB方法可以通過從接收信號中提取特征來區分信號,無需參數估計,計算復雜度低。FB性能主要取決于兩個因素:合適的特征集和有效的分類方法。多年來,人們對瞬時特征、高階統計量、循環平穩特征、星座形狀、時頻特征等各種特征進行了研究,以提升系統性能。

隨著深度學習在圖像識別領域得到廣泛應用,有學者利用時頻分析將信號轉化為時頻圖像(time-frequency images,TFIs),再經深度學習模型來自動提取信號的時頻特征。文獻[12]提出一種基于時頻分布和卷積神經網絡(convolutional neural network,CNN)的盲調制識別方法,將TFIs直接作為網絡的輸入,避免了傳統識別算法中復雜的人工特征提取和數據重構。但在低信噪比(signal to noise ratio, SNR)情況下,TFIs嚴重失真,深度學習網絡不能有效提取信號特征從而導致成功識別率低。因此,文獻[13]提出一種新的基于時頻變換的調制識別融合算法,將AlexNet提取到的信號細節特征與HuMoments表示的信號形狀特征進行融合,并利用廣義回歸神經網絡(generalized regression neural network,GRNN)對調制模式進行分類以進一步提高識別率。文獻[14]利用數字圖像處理技術將Choi-Williams變換得到的二維TFIs處理成二值圖像以降低噪聲干擾。然而,二值化處理會丟失TFIs的能量分布信息,從而降低信號的識別率。為了提取信號特征,文獻[15]通過自適應維納濾波算法濾除背景噪聲,再經連通域檢測算法將TFIs裁剪成適合CNN訓練的維度,該方法可以在一定程度上降低噪聲干擾,但提升識別率能力有限。

由于生成對抗網絡(generative adversarial network,GAN)具有較強的樣本模擬能力,在圖像去噪領域得到了成功應用。且GAN在處理圖像過程中無需人為設計參數,經該網絡重新生成的圖像能保持自身的細節紋理特征。因此,本文使用GAN對帶噪TFIs進行預處理,提出了一種基于GAN與CNN(GAN-CNN)的數字信號調制識別方案,主要由時頻處理、圖像去噪和分類識別3部分組成。第1部分利用平滑偽Wigner-Ville分布(smooth pseudo Wigner-Ville distribution,SPWVD)將所有信號轉換成時間和頻率的二維圖像,然后經雙線性插值對TFIs進行預處理。第2部分設計了嵌入剩余密集塊(residual dense block,RDB)的去噪GAN,可以直接提取TFIs的魯棒性特征,有效地去除TFIs中的噪聲。同時,通過構造重建損失與對抗損失的加權和損失函數,避免了低SNR條件下的圖像細節信息丟失。第3部分微調CNN中經典的剩余網絡(residual network, ResNet)模型來識別被處理的TFIs。仿真結果表明,所提出的GAN-CNN能有效降低TFIs中的噪聲干擾,提高了低SNR下的成功識別率。

1 信號模型與時頻分布

1.1 信號模型

接收到的數字調制信號如下:

()=()+()

(1)

式中:()是發送的調制信號,可以表示為

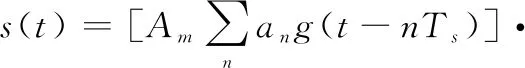
cos(2π(+)++)

(2)

式中:和分別是調制幅度和符號序列;()為符號周期內形成的波形脈沖;為符號周期;和表示載波頻率和調制頻率;和表示初始相位和調制相位;()為加性高斯白噪聲。

1.2 時頻分布

文獻[19]中使用短時傅里葉變換(short-time Fourier transform,STFT)來處理信號。雖然STFT可以表示信號的時頻域特征,但該方法時頻分辨率低,不適用于對時頻精度要求過高的場景。與STFT不同,Wigner-Ville分布使用信號的正負移位之積構成一種“雙線性形式”的變換。具有時頻分辨率高的特點,但會產生交叉項。為有效防止交叉項,使用平滑偽Wigner-Ville分布:

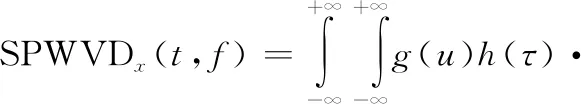
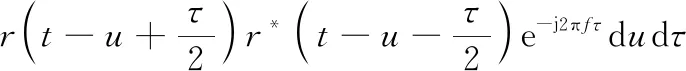
(3)

式中:和分別表示時間和頻率;()和()為窗口函數;(·)是(·)的共軛函數。

作為示例,圖1給出了幾種調制信號在SNR為-10 dB情況下的SPWVD變換情況。圖1中,橫向中心區域連續線狀體為調制信號,其余雜項為噪聲。由此可見,SPWVD雖可改善交叉項的影響,但在低SNR條件下TFIs仍存在部分失真。

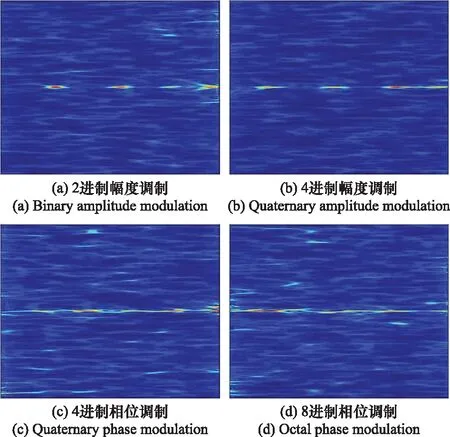
圖1 SNR=-10 dB下部分調制信號SPWVD生成圖Fig.1 SPWVD generation diagram of partial modulated signal at SNR=-10 dB

2 GAN-CNN的調制識別方案

如圖2所示,GAN-CNN主要由3部分組成:時頻處理、去噪網絡和識別網絡。有關時頻處理模塊已經在第1節介紹,下面將重點介紹GAN去噪網絡與CNN識別網絡的構造。

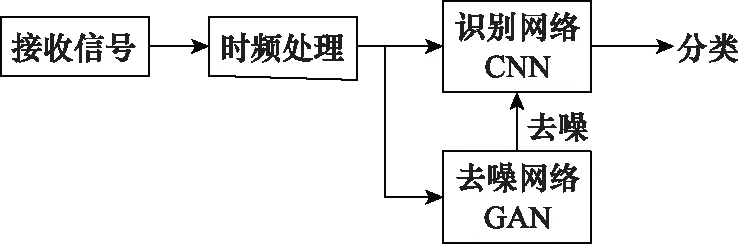
圖2 GAN-CNN的調制識別方案Fig.2 Modulation recognition scheme of GAN-CNN

2.1 用于圖像去噪的GAN結構

GAN由生成網絡和鑒別網絡兩部分組成,主要用于對帶噪TFIs進行去噪。為提高GAN輸出圖像的質量,將用于圖像超分辨率重建的RDB嵌入到生成器中,GAN的網絡結構如圖3所示。

2.1.1 生成網絡

生成網絡的目的是將帶噪圖像經非線性映射到去噪圖像。帶噪TFIs首先經過一個卷積核大小為7×7的卷積層來提取底層特征,并加入線性整流函數ReLU進行非線性映射。接著對TFIs進行下采樣處理以降低圖像的分辨率,卷積核為5×5,步長為2,并在卷積層后加入Dropout防止過擬合。然后利用6個RDB提取圖像的局部特征。最后經上采樣卷積塊重建去噪后的TFIs。

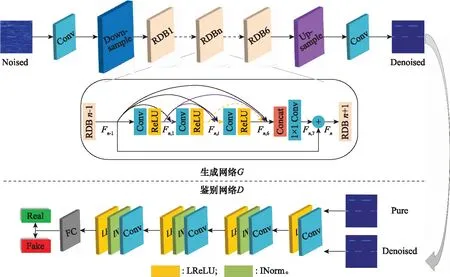
圖3 GAN的網絡結構Fig.3 Network structure of GAN

圖3生成網絡部分中給出了第個RDB的內部結構,通過將前一個RDB的狀態傳遞給當前RDB的每一層來實現連續存儲。-1作為第個RDB的輸入,為輸出。第個RDB中第個卷積層的輸出為

,=(,[-1,,1,,2,…,,-1]),
,∈{1,2,3,4,5,6}

(4)

式中:(·)表示ReLU激活函數;,是第個RDB中第個卷積層的權重;[-1,,1,,2,…,,-1]是括號內各特征映射的級聯表示。假設-1有個特征映射,每經過一個卷積層產生個特征映射,則共產生+(-1)個特征映射。隨著卷積層數量的增加,特征映射數量也隨之增加,從而導致訓練難度增大。為了減少特征映射數量,將第7個卷積層的大小設置為1×1,使得和-1的特征映射數目相等。最后,加入跳躍連接將淺層特征和深層特征相關聯,表示為=,7+-1。

212 鑒別網絡

鑒別網絡用于鑒別生成的去噪圖像與純凈圖像是否相似。本文設計的鑒別網絡為全卷積網絡,由4層卷積層組成,目的是對輸入的生成圖像和純凈圖像進行特征提取。圖3顯示的鑒別網絡中“LReLU”表示Leakey-ReLU激活函數,“INorm”表示實例規范化,且全部使用卷積核為5×5的卷積層,最后通過全連接層,由Sigmoid輸出判決結果。

2.1.3 損失函數

損失函數采用重建損失與對抗損失的加權和:

=+

(5)

式中:是超參數;和分別為重建損失與對抗損失。

重建損失函數表示為

(6)

對抗性的損失也被稱為GAN損失。設為用于訓練的真實圖像數據,為噪聲數據,GAN損失可以表示為

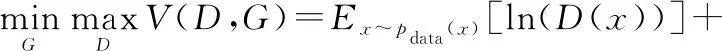
(7)

式中:(,)表示GAN聯合損失;()為圖像數據集的分布;()為噪聲的分布;()是鑒別器預測真實圖像的結果;()是經生成器生成的假圖像;(())表示鑒別器預測假圖像的結果。

在訓練的生成階段,希望生成的圖像越接近真實圖像越好,即要求(())盡可能的大,最佳結果為(())=1,此時鑒別器將所有的假圖像都預測為真圖像。因此對于生成器,(,)越小越好:

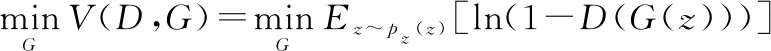
(8)

然后,生成器將通過降低其梯度來更新權重:

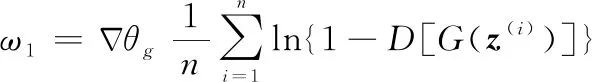
(9)

式中:是訓練數據批大小;()是小批量數據中的噪聲向量。

在訓練的鑒別階段,的能力越強則()越大,同時(())越小,故的最佳結果是()=1和(())=0。因此對于鑒別器,(,)越大越好:

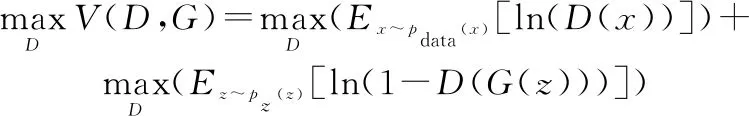
(10)

更新權重:

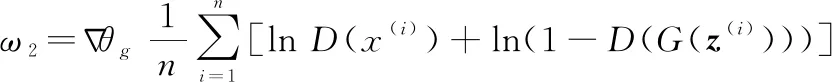
(11)

令′={,}、′={,},其中=()表示經生成的去噪圖像。最后,對抗性損失可表示為

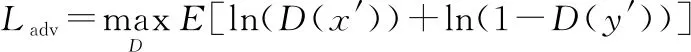
(12)

該損失函數可緩解式(6)所產生的過擬合問題。

GAN的具體流程如下所示。

算法 1 GAN輸入 純凈圖像Ipure,帶噪圖像Inoised輸出 去噪圖像Idenoisedfor 訓練迭代次數 do1.樣本n批處理純凈集圖像Ipure與帶噪集圖像Inoised2.經生成器G得生成去噪圖像Idenoised←G(Inoised)3.將x'定義為{Inoised,Ipure}、y'定義為{Inoised,Idenoised}4.LD←1n∑n1 ln(Dw(x'))+ln(1-Dw(y')) 5.通過Adam(w,LD,α)更新鑒別器D6.LG←1n∑n1 ln(Dw(x'))+ln(1-Dw(y')) + λ1n∑n1Ipure-Gθ(Inoised)17.通過Adam(θ,LG,α)更新生成器Gend

2.2 用于識別的CNN結構

如圖4所示,CNN由輸入層、卷積層、池化層、全連接層和輸出層組成。其中,卷積層是CNN的重要組成部分,通過卷積核作用于局部區域來獲取局部信息。池化層用于壓縮輸入特征映射,簡化了網絡的計算復雜度。全連接層結合了輸入數據的所有特征,并將輸出值發送給分類器。

圖4 CNN的網絡結構Fig.4 Network structure of CNN

文獻[21]指出隨著網絡深度的增加不僅不能提升系統性能,反而會導致模型收斂變慢、效果變差。為緩解網絡退化問題,引入殘差結構,允許任意低層的特征映射直接傳播到高層。同時,殘差結構使模型更易于優化。因此,本文采用ResNet作為特征提取器,并使用批標準化(batch normalization,BN)來加速網絡的收斂速度以提升準確率。主要工作為以下兩點。

2.2.1 BN

對于一個擁有維的輸入=(,…,(),…,()),對其每個維度進行BN處理可表示為

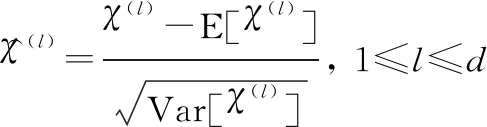
(13)

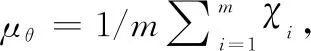
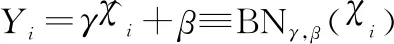
(14)

式中:和是兩個需要學習的參數。

222 特征提取

本文采用遷移學習的方法來加快訓練效率。因TFIs不同于網絡預訓練模型所使用的大規模自然圖像,引入一個微調的ResNet模型以滿足訓練要求。首先,刪除ResNet模型的最后一層全連接層,以確保網絡輸出同調制類型數量相同。其次,在最后一個卷積層之后加入池化層,以減少參數數量,提升網絡性能。最后,將學習率設置為0.001,以避免模型權重扭曲過快。

為了分析所提網絡的內部操作,在提取TFIs特征時,對首層卷積和末層卷積做了可視化輸出。圖5顯示了64個像素為112×112的低階特征。圖6顯示了前256個像素為7×7的高階特征。對比圖5與圖6可以發現,首層提取到的TFIs特征較接近送入網絡的初始TFIs,而末層提取到的特征更趨于多樣化,這也更有利于分類。

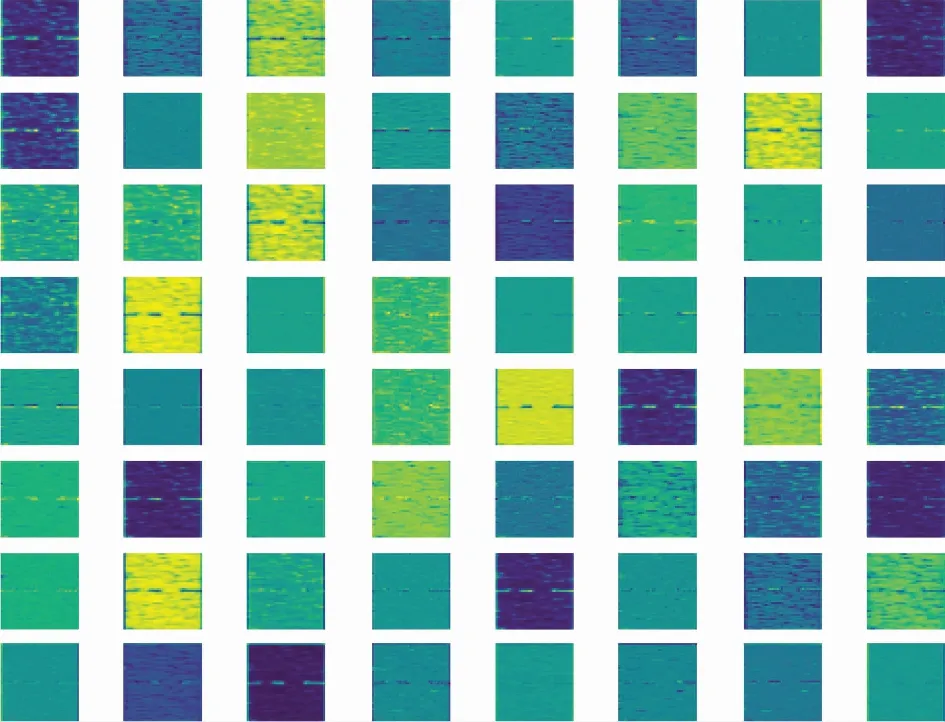
圖5 首層卷積輸出Fig.5 First convolution layer output

圖6 末層卷積部分輸出Fig.6 Output of the last layer convolution section

3 仿真分析

本節首先給出了實驗信號的參數設置以及實驗流程。其次,為了驗證GAN-CNN的有效性,在同數據下對文獻[13-15]所用算法進行了性能對比。然后,為了分析去噪處理對該方案的影響,做了對比實驗。最后,對文中所涉算法進行了計算復雜度比較。

3.1 實驗數據及實驗流程

3.1.1 參數設置

本文對二進制振幅鍵控(2-ary amplitude shift keying，2ASK)、四進制振幅鍵控(4-ary amplitude shift keying，4ASK)、二進制頻移鍵控(2-ary frequency shift keying，2FSK)、四進制頻移鍵控(4-ary frequency shift keying，4FSK)、八進制頻移鍵控(8-ary frequency shift keying，8FSK)、二進制相移鍵控(2-ary phase shift keying，2PSK)、四進制相移鍵控(4-ary phase shift keying，4PSK)、八進制相移鍵控(8-ary phase shift keying，8PSK)和16進制正交幅度調制(16-ary quadrature amplitude modulation，16QAM)共9種常用的數字調制信號進行識別。信號的參數設置如下:采樣頻率為64 kHz,載波頻率為16 kHz,碼元數目為128,每個信號產生10個符號數。所有的信號源都是在Matlab 2017b中創建的。對于GAN,按SNR[-10 dB∶2 dB∶8 dB]各生成900個帶噪樣本及900個純凈樣本,再經SPWVD共轉換成9 000個帶噪圖像和9 000個純凈圖像,取其中700對作為GAN訓練集,200對為測試集;對于CNN網絡,在相同的SNR條件下,每個信號隨機產生1 000個樣本,SNR按[-10 dB∶2 dB∶8 dB]共產生90 000個樣本,經SPWVD得到各信號不同SNR下的TFIs。

3.1.2 尺寸調整

因ResNet的輸入尺寸限制,本文通過雙線性插值將信號的二維TFIs大小調整為224×224以便數據處理。假設原始圖像大小為×,調整后圖像×的像素點可以表示為

(,)=(+,+)=(1+)(1-)(,)+
(1-)(,+1)+(1-)(+1,)+(+1,+1)

(15)

式中:和分別是的整數和小數部分;和是的整數和小數部分。

313 實驗流程

GAN-CNN實驗流程如下。

SPWVD將調制信號轉換為TFIs,其大小為1 024×1 024。

TFIs經線性插值固定為224×224。

GAN對預處理的TFIs進行訓練,訓練結束保留網絡參數。

用于識別的90 000個樣本經GAN去噪后按9∶1劃分CNN訓練集與測試集。

經步驟4去噪后的圖像作為CNN的輸入,經微調的ResNet模型識別數字信號的調制類型。

3.2 實驗結果分析

3.2.1 所提方案分類精度

為了更好地說明GAN-CNN的性能,本文與文獻[13-15]中的方案進行了比較。圖7顯示了不同方法的成功識別概率與SNR的關系。

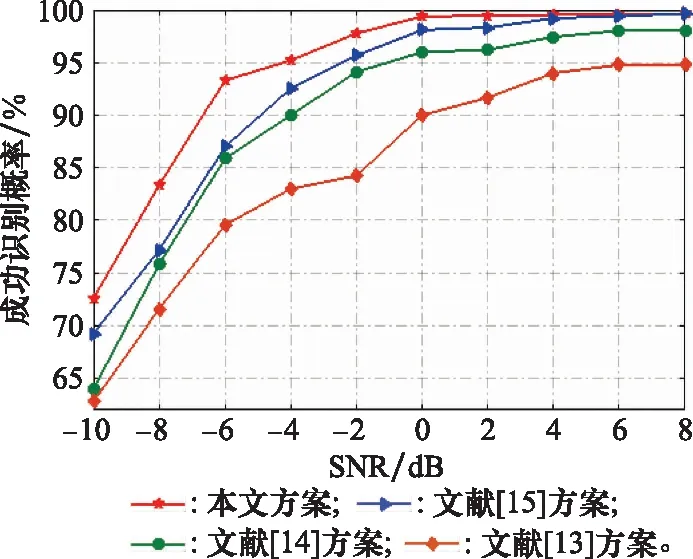
圖7 不同方案識別結果對比Fig.7 Comparison of identification results of different methods

在圖7中,文獻[13]所提方案在所有方案中表現欠佳,這是由于在將AlexNet提取到的特征與HuMoments提取的特征進行融合時,為避免高維帶來的大量計算而使用t-分布隨機鄰居嵌入(t-distributed stochastic neighbor embedding, t-SNE)對AlexNet數據進行降維,從而導致TFIs部分特征丟失,且并未消除低SNR條件下噪聲對TFIs的影響。文獻[14]雖對TFIs進行了預處理以消除背景噪聲,但在將TFIs二值化的過程中丟失了調制信號的細節特征。文獻[15]所提方案未經二值化處理,保有信號原始特征,但在低SNR條件下成功識別率明顯低于所提方案,這表明本文所提調制識別方案GAN-CNN的去噪效果優于文獻[15]所使用的自適應維納濾波算法。此外,隨著SNR的降低,各方案分類精度也會降低,但總體而言,GAN-CNN的性能最佳。

GAN-CNN網絡對各信號的成功識別概率隨SNR的變化曲線如圖8所示。隨著SNR的增大,各調制信號的分類準確度增大,SNR為-4 dB時,所有調制信號分類準確度均達到90%及以上。當SNR大于0 dB時,各調制信號的分類準確度接近100%。

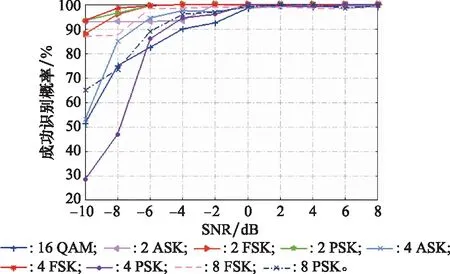
圖8 9種調制信號類型的識別率Fig.8 Recognition rate of nine modulation signal types

為了探究在低SNR條件下限制正確識別概率的因素,圖9給出了4種方法在-10 dB SNR下的混淆矩陣。

如圖9(a)所示,2PSK和4FSK的分類精度處于較高水平,而4ASK和4PSK的誤差高于其他調制類型。如圖1所示,2ASK與4ASK、4PSK與8PSK的TFIs像彼此相似,故4ASK與2ASK、4PSK與8PSK極易混淆。通過與圖9(b)、圖9(c)和圖9(d)對比可得,不同的識別方案對調制信號種類的敏感度不同,但所提方案GAN-CNN的混淆矩陣相對集中,對大部分調制類型的正確分類概率也高于其他3種方案。

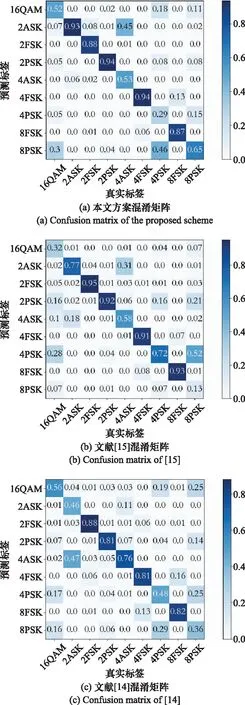
圖9 SNR=-10 dB下不同方法的混淆矩陣Fig.9 Confusion matrix of different methods at SNR=-10 dB

3.2.2 GAN的影響

為了分析GAN網絡對該方法分類精度的影響,對GAN-CNN網絡和去GAN的分類網絡進行了測試。圖10所示,在各SNR下,經GAN預訓練的網絡識別率均高于直接訓練的網絡。在SNR為-10 dB時,經GAN預訓練的分類網絡的分類精度達到73%,而未經GAN訓練的分類網絡的分類精度僅為65%。同時觀測到在低SNR下成功識別率的提升要高于相對較高SNR情況下。這也說明低SNR下噪聲的存在使信號特征不明顯,TFIs在不同的類之間更趨于一致,因此更需要GAN來消除噪聲影響。

圖10 GAN對分類網絡性能的影響Fig.10 Impact of GAN on classification network performance

圖11給出SNR為-10 dB時,GAN網絡處理16QAM信號的前后TFIs。在較低SNR情況下,16QAM信號的輸入圖像受到嚴重的噪聲污染,信號特征不清晰。經GAN處理后,重建的去噪圖像包含原始信號的細節信息,同時背景噪聲幾乎消失,信號特征明顯。因此,GAN有助于提取TFIs的魯棒特征,最終提高了本文方案的抗噪性能。

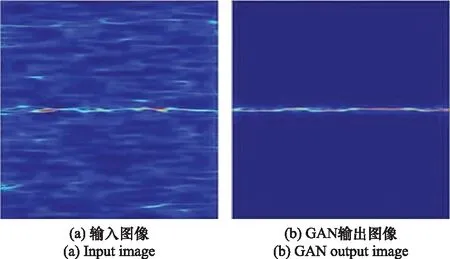
圖11 SNR=-10 dB下GAN處理16QAM信號前后TFIsFig.11 TFIs before and after GAN processing 16QAM signal at SNR=-10 dB

3.2.3 計算復雜度比較

為了更有效地評估所涉及算法的計算復雜度,對不同方案的平均訓練速度進行了比較。如圖12所示,文獻[13]所提方案每秒可處理11.67幅TFIs,本文所提方案處理速度略低于文獻[13],但明顯高于文獻[14-15]。這是由于本文與文獻[13]在對TFIs進行訓練時,采用了遷移學習的方法提升了訓練速度。文獻[13]使用GRNN對調制信號進行識別,該網絡較本文使用的ResNet網絡模型參數少、訓練時間短,但識別精確度不如ResNet。因此,綜合考慮訓練速度與識別精度,本文所提出的GAN-CNN具有較強競爭力。

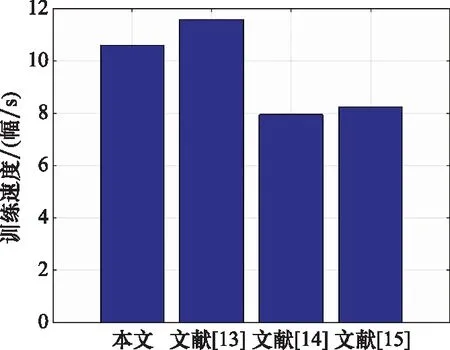
圖12 不同方案訓練速度比較結果Fig.12 Comparison result of training speed of different programs

4 結 論

本文針對低SNR條件下TFIs失真導致成功識別率較低的問題,提出了一種基于GAN和CNN的數字信號調制識別方法。GAN去噪網絡去除了噪聲的干擾,使低SNR下大量的信號特征得以保留,從而提高分類網絡的分類精度。CNN識別網絡使用微調的ResNet模型,其優秀架構具有強大的分類能力,同時采用遷移學習來提升訓練效率。實驗結果表明,GAN-CNN可以準確識別9種數字調制信號,在SNR為-6 dB時,識別成功率達到93%以上,具有較強的抗噪聲性能。