基于時間序列數據擴增和BLSTM的滾動軸承剩余壽命預測方法

孫世巖, 張 鋼, 梁偉閣, 佘 博, 田福慶

(海軍工程大學兵器工程學院, 湖北 武漢 430033)

0 引 言

滾動軸承是旋轉機械重要組成部件,其運行狀態好壞將直接影響整個旋轉機械系統的安全與否。滾動軸承在工作時發生故障,會造成停機事故,影響生產進度,導致經濟損失甚至人員傷亡。因此,監測滾動軸承運行狀態,預測滾動軸承剩余壽命對于提高系統可靠性、制定合理的維修計劃具有重要意義。

目前,滾動軸承剩余壽命預測方法主要分為兩類:機理模型驅動的剩余壽命預測方法和數據驅動的剩余壽命預測方法。其中,機理模型驅動的剩余壽命預測方法需要準確建立滾動軸承性能退化模型。但是在實際工程應用中,滾動軸承性能退化過程機理較為復雜,難以建立各類滾動軸承準確的機理模型。數據驅動的剩余壽命預測方法是利用傳感器監測數據,通過各種算法挖掘歷史監測數據中的性能退化信息,建立性能退化模型,進而預測剩余壽命。由于數據驅動的剩余壽命預測方法不需要建立復雜的機理模型,且能夠充分利用各類傳感器的監測數據,逐漸成為研究熱點。數據驅動的剩余壽命預測方法主要包括兩大類:基于統計學的剩余壽命預測方法和基于智能學習的剩余壽命預測方法。其中,基于統計學的方法需要首先假定機械設備性能退化過程符合相應的統計學模型,然后利用監測數據對模型參數進行估計,最后利用模型預測性能退化趨勢,進而得到機械設備剩余壽命。因此,機械設備性能退化統計學模型選擇是否恰當將直接影響剩余壽命預測精度。智能學習模型能夠通過智能算法從監測數據中自主學習機械設備性能退化模式,預測剩余壽命,不需要事先構建物理模型或者統計模型,逐漸成為研究熱點。

深度學習作為一類智能算法,以其自適應特征提取能力、非線性函數表征能力獲得越來越多的關注,被廣泛應用于剩余壽命預測領域。Meng等提出一種基于深度卷積長短期記憶網絡剩余壽命預測方法,將多個深度卷積長短期記憶網絡逐層疊加,形成編碼預測體系,建立了滾動軸承剩余壽命預測模型。She等提出一種基于雙向門控循環神經網絡的剩余壽命預測方法,采集滾動軸承全壽命周期振動加速度數據驗證了所提方法的有效性。以上基于深度學習網絡的剩余壽命預測方法能夠有效提高預測精度。但是,深度學習網絡訓練過程需要大量監測數據,而滾動軸承全壽命周期試驗耗費時間長、成本高,無法進行大規模試驗。動態時間規整算法被廣泛應用于測量兩組不同時間序列數據之間的相似性。本文擬在已知滾動軸承全壽命周期運行數據的基礎上,利用動態時間規整算法擴增性能退化過程相似的滾動軸承運行數據,為雙向長短時記憶(bidirectional long-short term memory, BLSTM)網絡提供觀測數據,提高剩余壽命預測精度。

1 理論介紹

動態時間規整(dynamic time warping, DTW)算法比較兩組異步信號,通過尋找最優匹配路徑來衡量其相似性。動態時間規整算法目前被廣泛應用于處理時間序列信號,例如語音識別。假設有兩組不同長度的時間序列信號={,,…,}和={,,…,},其序列長度分別是和。

長短時記憶(long-short term memory, LSTM)網絡是一類特殊的循環神經網絡，通過在網絡中添加記憶單元，能夠有效避免循環神經網絡在長期預測過程中出現的梯度消失或爆炸問題，被廣泛應用于剩余壽命預測領域。

1.1 動態時間規整

(1) 構造代價矩陣

動態時間規整算法的第一步是構造×代價矩陣,矩陣元素為

(,)=|-|

(1)

用于度量兩組信號數據的差異性。與越相似,則(,)越小(低代價);否則與差異越大,(,)越大(高代價)。動態時間規整算法的目標即為尋找使得兩組信號和總體代價矩陣數值最小的路徑。

(2) 規劃路徑

規劃路徑為一個序列,=(,,…,),其中=(,)∈[1∶]×[1∶],?∈[1∶],通過分配信號的元素到信號的元素來定義兩個間的路徑。規整路徑滿足如下約束條件。

邊界條件:

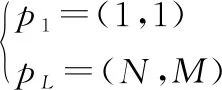
(2)

單調性條件:

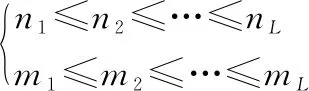
(3)

步長條件:

+1-∈{(1,0),(0,1),(1,1)},∈[1∶-1]

(4)

(3) 計算累計代價值

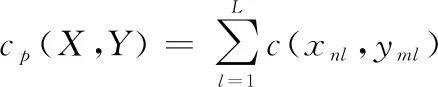
(5)

(4) 選取最佳路徑

選取最佳路徑即是選擇使得累計代價值最小的路徑,信號和之間的最優規整路徑的距離定義為

(,)=*(,)=min{(,)}

(6)

可以通過定義累計代價矩陣(,)來尋找最優路徑,(,)滿足一下約束條件

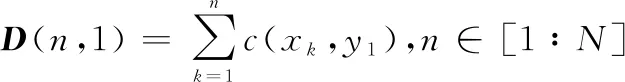
(7)

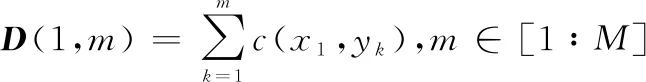
(8)

(,)=(,)+min{(-1,-1),(-1,),
(,-1)},2≤≤; 2≤≤

(9)

當累計代價矩陣確定后,最優路徑即為

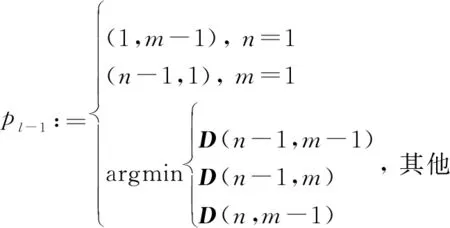
(10)

1.2 LSTM網絡

LSTM網絡是一類特殊的循環神經網絡,通過在網絡中添加記憶單元,能夠有效避免循環神經網絡在長期預測過程中出現的梯度消失或爆炸問題,被廣泛應用于剩余壽命預測領域。LSTM網絡的結構如圖1所示。

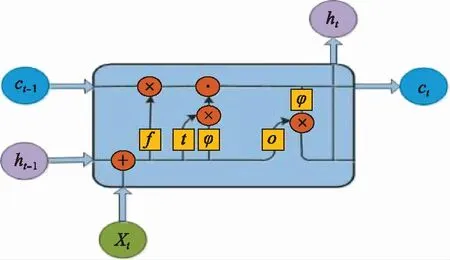
圖1 LSTM網絡單元結構Fig.1 Structure of LSTM network unit

LSTM網絡的記憶單元包括輸入門、輸出門、遺忘門。時刻記憶單元的更新過程如下所示:

=(+-1+)

(11)

=(+-1+)

(12)

=(+-1+)

(13)

=tanh(+-1+)

(14)

=·-1+·

(15)

=·tanh()

(16)

式中:,,,,,分別表示輸入門、輸出門、遺忘門、輸入的輸出值、單元體的狀態值、隱藏層輸出值。,,,,,,,是權重矩陣;,,,是偏置項。

1.3 BLSTM網絡

BLSTM基本原理與LSTM相同。第1.2節中介紹的LSTM網絡原理式(11)～式(16)即定量表征了BLSTM網絡的正向計算過程,可統一表示為

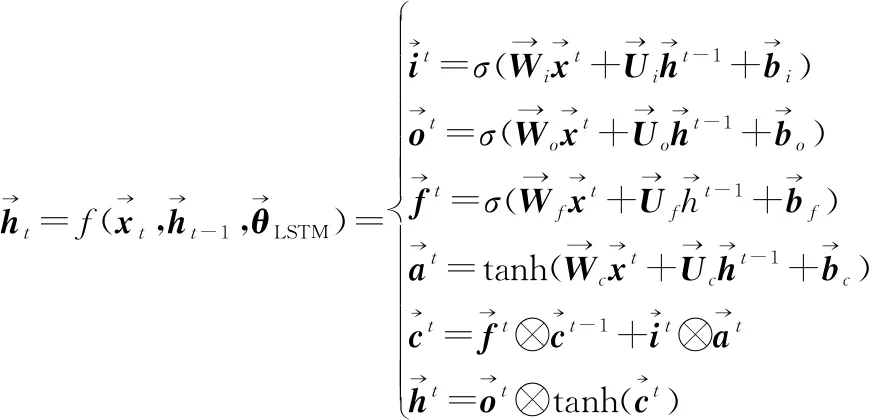
(17)

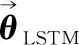
式(17)定量表征了正向LSTM單元內部計算過程,逆向LSTM單元內部計算過程如下:

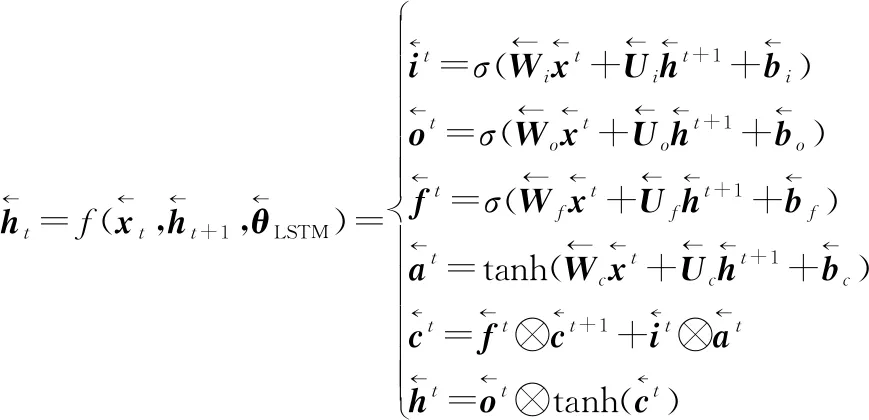
(18)

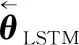
2 基于數據擴增的剩余壽命預測方法

本文提出的基于數據擴增模型和BLSTM網絡的剩余壽命預測方法如圖2所示。滾動軸承狀態監測數據有振動信號、聲信號、溫度信號等。其中,振動信號采集方便且對軸承性能退化過程敏感,被廣泛應用于軸承剩余壽命預測領域。本文從振動加速度信號提取特征,作為滾動軸承性能退化指標,即健康因子。提取滾動軸承全壽命周期振動加速度信號健康因子作為參考數據集,提取測試軸承振動加速度信號健康因子作為目標數據集。以參考數據集和目標數據集為基礎,利用數據擴增模型得到目標數據集擴增后的數據。最后,將擴增后的數據作為觀測數據輸入到BLSTM網絡預測剩余壽命。

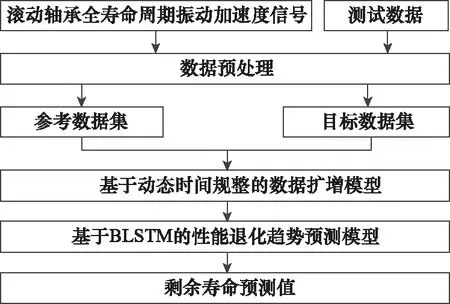
圖2 基于數據擴增和BLSTM的剩余壽命預測方法Fig.2 Remaining useful life prediction method based on data augmentation and BLSTM

2.1 數據預處理

工程實際應用中,采集到的振動信號含有大量噪聲,且不同工況下的振動信號不是理想的相似信號,因此需要對其進行預處理。

文采用移動平均(moving average, MA)平滑濾波法進行濾波處理,能夠對子矩陣內的數據點進行計算,求取平均值,與低通濾波器功能相當,模型數學表示為

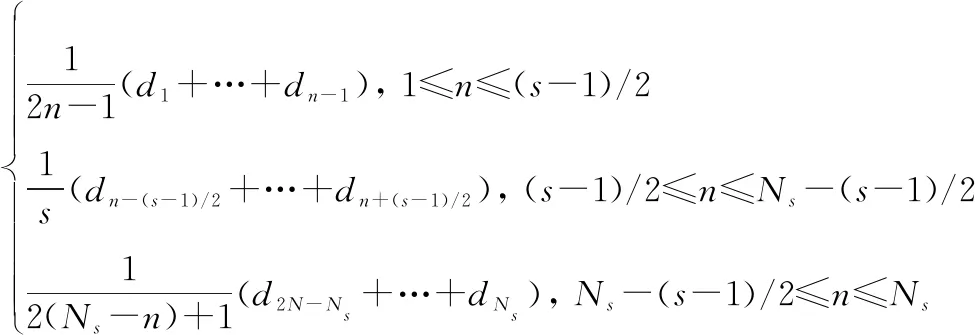
(19)

式中:為濾波后健康因子值總個數;是濾波參數,?;為第個原始健康因子值;MA是經過濾波處理得到的健康因子數據點。

2.2 基于DTW的數據擴增模型

DTW算法常用于測量兩組時間序列數據之間的相似性,本節將利用動態規整算法建立數據擴增模型。下面,以剩余壽命預測領域常用的指數退化函數為例,說明基于DTW的數據擴增模型建立過程。

假設某設備性能退化過程符合指數退化規律,即滿足:

=exp()

(20)

式中:表示性能退化指標;表示運行時間;是與運行工況有關的模型參數。

如圖3所示,已知該設備在工況1下,=05,運行周期為5的全壽命周期運行曲線。相同型號設備在工況2下,=03,運行周期為4。利用DTW模型擴增工況2下的數據至失效閾值,模型建立步驟如下。

建立參考數據集和目標數據集。圖3中,黑色虛線以下的藍色實點構成參考數據集,紅色實點構成目標數據集。

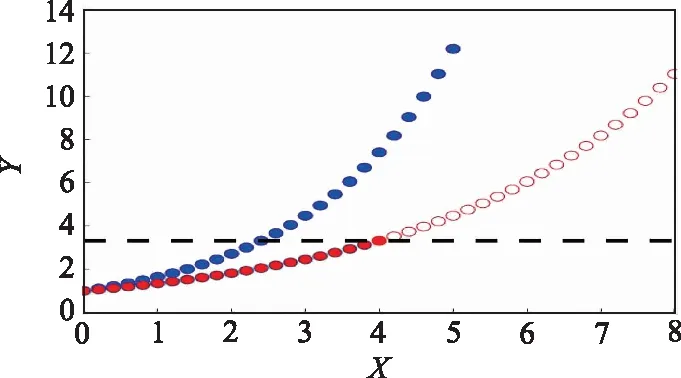
圖3 指數函數數據擴增示意圖Fig.3 Schematic diagram of exponential function data augmentation

計算最優路徑。利用式(1)～式(11),計算參考數據集和目標數據集之間的動態規整最優路徑曲線,結果如圖4所示。圖4中,藍色空心點表示最優路徑點,符合線性分布,因此對其進行線性擬合,得到擬合參數,擬合曲線為圖4中的紅色直線(紅色虛直線表示擬合結果的置信區間)。

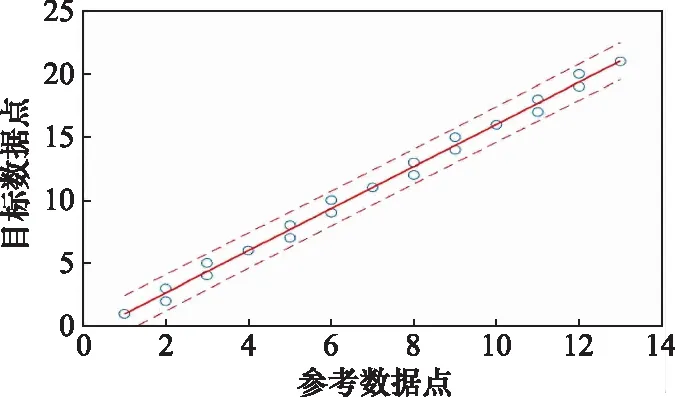
圖4 DTW最優路徑Fig.4 Optimal path of DTW

擴增數據。利用工況1下除參考數據集外的剩余數據,根據步驟2中得到的擬合參數,計算得到擴增數據,如圖3中紅色空心點所示。

2.3 基于觀測數據和BLSTM網絡的剩余壽命預測模型

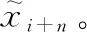
3 試驗驗證

為了驗證本文所提方法的有效性,本節利用滾動軸承全壽命周期試驗進行驗證,并與幾類常用的剩余壽命預測方法進行對比分析。

3.1 試驗介紹

本文使用的試驗數據是XJTU-SY滾動軸承全壽命周期試驗數據集。

滾動軸承全壽命周期試驗平臺主要組成包括:交流電動機、電動機轉速控制器、轉軸、滾動軸承和液壓加載系統,如圖5所示。試驗時,利用電動機轉速控制器控制交流電動機轉速,通過轉軸帶動兩個滾動軸承轉動。同時,利用液壓加載系統可以對滾動軸承施加徑向力,通過設定不同的徑向力得到不同工況下的全壽命周期運行數據。數據采集頻率為25.6 kHz,采樣時間為1.28 s,采樣間隔為1 min。

圖5 XJTU-SY滾動軸承全壽命周期試驗平臺Fig.5 Experimental platform of XJTU-SY rolling bearing life cycle

試驗所用軸承型號為LDK UER204軸承,通過設定不同的徑向力共開展了3種運行工況下的滾動軸承全壽命周期試驗,每類工況包括5組試驗。各工況條件如表1所示。

表1 試驗工況

由于液壓加載系統提供的徑向力位于水平方向,因此布置在水平方向的振動加速度傳感器獲取的性能退化信息更加豐富。

水平方向布置的振動加速度信號采集到的振動加速度值隨時間變化過程如圖6所示。

圖6 水平方向的原始振動加速度信號Fig.6 Original vibration acceleration signal of horizontal direction

由圖6可知,滾動軸承在前期未出現早期故障時的運行過程中振動加速度值隨時間變化的的波動不大,基本處于平穩狀態,無法反應其性能退化過程。在滾動軸承運行后期,振動加速度信號幅值隨時間變化而不斷增加,性能退化特征明顯,可以用于預測剩余壽命。本文采用文獻[18]提供的自適應性能退化檢測方法判斷滾動軸承性能退化階段開始時刻,即可作為剩余壽命預測的起始時刻。同時,為保證試驗安全,本試驗將振動加速度幅值20作為滾動軸承失效閾值。

本文采用均方根(root mean square, RMS)值作為反映滾動軸承運行狀態的健康因子。數據擴增模型應用的前提是兩類設備具有相似的性能退化過程,僅運行工況存在差異。本文選取工況1下的bearing1_1軸承全壽命周期數據作為訓練數據,選取工況2下的bearing2_5和工況3下的bearing3_1作為測試數據。3組軸承的全壽命周期運行曲線如圖7所示。3組不同工況下的滾動軸承最終都出現外圈損傷。由圖7可知,3組軸承的性能退化過程相似。以bearing1_3軸承的全壽命周期數據作為訓練集,分別與測試軸承bearing2_5和bearing3_1建立動態時間規劃模型。根據文獻[20]提出的自適應性能退化檢測方法確定各個軸承性能退化起始點。3組軸承性能退化階段的健康因子分布情況如圖8所示。

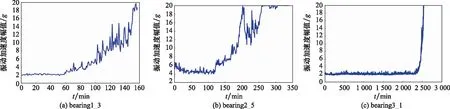
圖7 滾動軸承全壽命周期運行曲線Fig.7 Life cycle running curve of rolling bearing

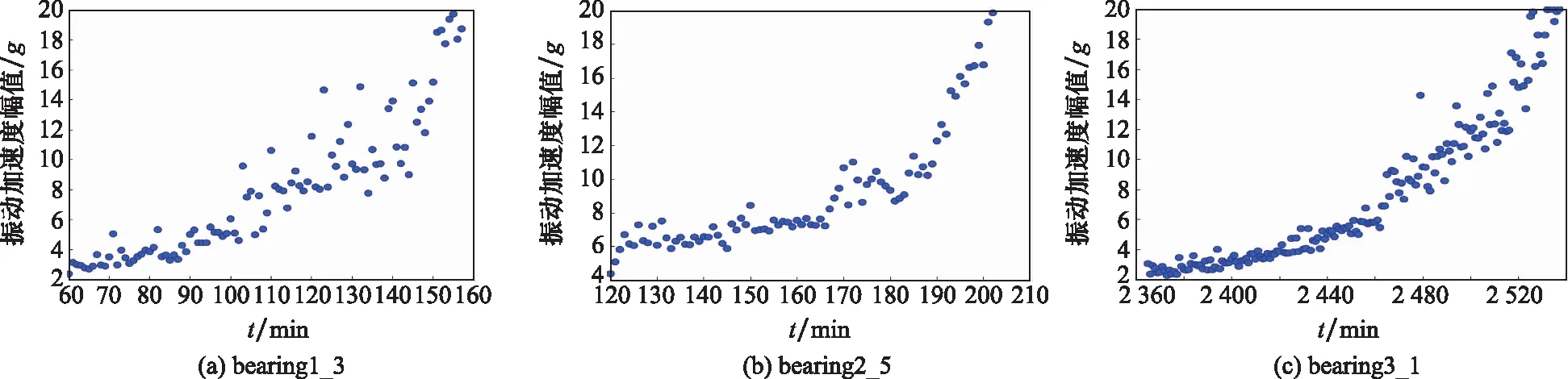
圖8 滾動軸承性能能退化階段健康因子分布圖Fig.8 Health indicator distribution diagram of rolling bearing performance degradation stage

由圖8可知,各軸承性能退化狀態分布存在大量噪聲,不利于尋找最優路徑。本文分別利用指數模型、雙指數模型、Paris裂紋模型對訓練數據bearing1_3的性能退化狀態進行回歸擬合,得到擬合結果如表2所示。

表2 擬合優度

由表2可知,指數模型對訓練數據性能退化狀態擬合效果最佳。因此,選取指數模型作為擬合函數。假設噪聲分布～N(0,),計算健康因子到擬合曲線之間的距離,得到噪聲分布的均值和方差。同時,由圖8可知,3組滾動軸承的性能退化起始點各不相同,無法直接建立數據擴增模型。本文提出一種基于虛擬擬合點的動態時間規整數據集構建方法。利用擬合曲線建立起始時間為0的虛擬擬合點,如圖9所示。

圖9 虛擬擬合點示意圖Fig.9 Schematic diagram virtual fitting points

圖9中,紅色實心點為實測數據,紅色空心點為利用擬合曲線構建的虛擬擬合點。利用構建好的虛擬擬合點建立動態時間規劃模型。如圖10所示,藍色空心散點表示訓練集bearing1_3的虛擬擬合點構建的參考數據集,紅色空心散點表示測試集bearing2_5的虛擬擬合點組成的目標數據集。利用虛擬擬合點組成的性能退化曲線建立動態時間規劃模型,確定最優規劃路徑。

圖10 虛擬擬合點數據集Fig.10 Virtual fitting point dataset

測試軸承bearing2_5和bearing3_1與訓練集bearing1_3的最優規劃路徑如圖11所示。

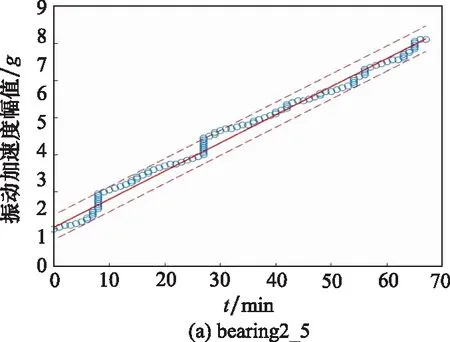
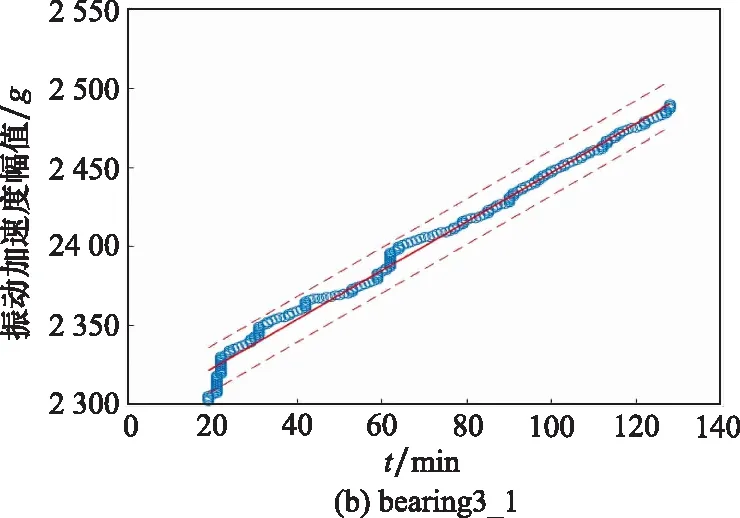
圖11 測試軸承最優路徑規劃Fig.11 Optimal path planning of test bearings

由圖11可知,測試數據與訓練數據之間的最優路徑基本符合線性分布,說明3種不同工況下的性能退化模式基本一致。得到最優規劃路徑后,即可利用訓練數據集中非參考數據計算得到擴增后的測試數據,如圖12和圖13所示。圖12和圖13中,藍色實心點表示訓練數據集中的參考數據點,紅色實心點表示測試數據中的目標數據點。藍色空心點表示訓練集中的非參考數據點,用于預測測試集的擴增數據。紅色空心點表示動態時間規整擴增得到的測試數據。紅色虛線表示失效閾值,黑色虛線表示參考數據集與目標數據集范圍閾值。

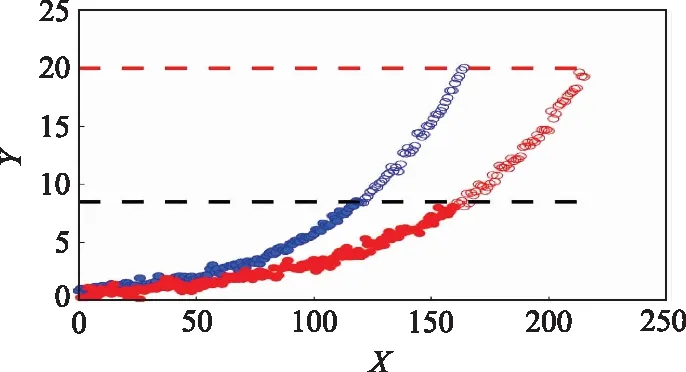
圖12 bearing2_5數據擴增示意圖Fig.12 Schematic diagram of bearing2_5 data augmentation

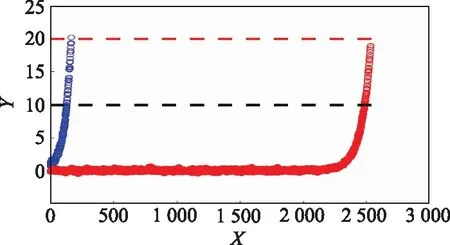
圖13 bearing3_1數據擴增示意圖Fig.13 Schematic diagram of bearing3_1 data augmentation

將原始測試數據與擴增得到的測試數據相空間重構后輸入至BLSTM網絡中預測測試軸承性能退化趨勢。BLSTM的網絡參數如表3所示。

表3 BLSTM網絡參數

兩組測試軸承性能退化預測結果如圖14和圖15所示。圖14和圖15中,藍色曲線表示測試軸承實際性能退化曲線;紅色點線表示性能退化過程預測值。

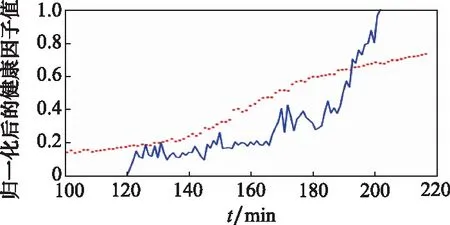
圖14 bearing2_5性能退化預測圖Fig.14 Performance degradation prediction diagram for beairng2_5

圖15 bearing3_1性能退化預測圖Fig.15 Performance degradation prediction diagram for beairng3_1

由圖14和圖15可知,利用擴增數據訓練的BLSTM網絡能夠有效預測滾動軸承性能狀態變化趨勢,為預測剩余壽命奠定了基礎。

為了對比擴增數據對提高BLSTM網絡預測能力的效果,采用BLSTM網絡對原始測試數據進行迭代預測,預測結果如圖16所示。

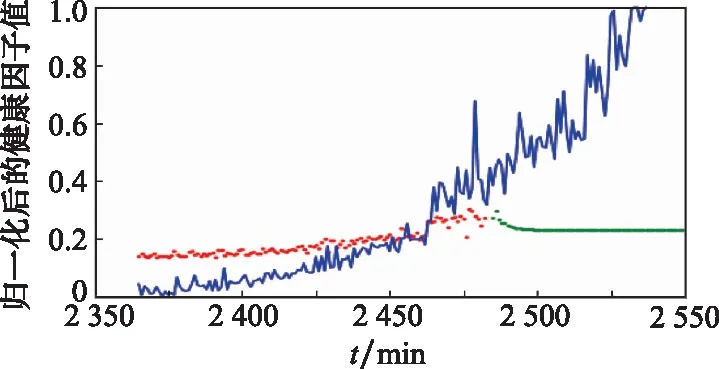
圖16 性能退化過程迭代預測結果Fig.16 Iterative prediction results of performance degradation process

圖16中,藍色曲線表示測試軸承實際性能退化曲線,紅色點線表示訓練數據預測結果,綠色點線表示迭代預測結果。由圖16可知,訓練數據預測結果與性能退化趨勢基本相符,說明網絡有效學習到訓練數據中的性能退化趨勢,但是迭代預測過程中,預測誤差不斷增大,最終導致性能退化趨勢偏離實際結果。將圖14和圖15對比可知,通過數據擴增模型提供更多的觀測數據,能夠有效避免迭代預測過程誤差不斷積累造成的結果偏差,提高了LSTM的預測精度。

3.2 對比分析

根據文獻[24],滾動軸承剩余壽命預測結果的定量表征式為

RUL()=inf{:(+)≥|}

(21)

式中:RUL()是自預測起始時刻的剩余壽命;(+)是+時刻預測的性能退化狀態;表示所有的健康因子值組成的集合,是失效閾值,本文采用20。

為定量分析本文所提方法對提高剩余壽命預測結果精度的有效性,分別利用本文所提方法、基于相關向量機的方法、基于深度置信網絡的方法和基于粒子濾波的方法預測滾動軸承bearing1_3的剩余壽命,并與實際的剩余壽命值進行對比,結果如圖17所示。圖17中,橫坐標表示剩余壽命預測起始時刻,縱坐標表示對應的剩余壽命值;黑色矩形線段表示實際剩余壽命,剩余壽命值隨預測起始時刻的增加呈現線性變化規律;紅色圓形線段表示基于數據擴增和BLSTM的剩余壽命預測結果,初始時刻剩余壽命預測值偏離實際值較大,隨著預測起始時刻的增加,擴增數據也不斷增多,預測結果不斷接近實際值;藍色上三角線段表示基于RVM的剩余壽命預測結果,但是隨著預測起始時刻的增加,預測值與實際值仍存在一定的偏差;綠色下三角線段表示基于深度置信網絡(deep belief network, DBN)的剩余壽命預測結果,屬于典型的數據驅動的方法,由于數據量較小,導致預測值與實際值存在偏差;紫色菱形線段表示基于粒子濾波(particle filtering, PF)算法的剩余壽命預測結果,采用Paris-Erdogan機理模型刻畫滾動軸承性能退化過程,利用粒子濾波算法更新模型參數,由于考慮了性能退化機理,因此預測結果能夠較快收斂于實際值,但隨著預測起始時刻的增加,預測結果精度沒有明顯提高。

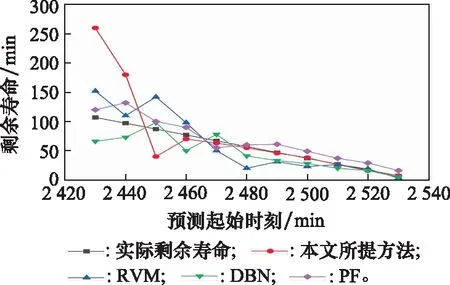
圖17 剩余壽命預測結果對比圖Fig.17 Comparison diagram of remaining useful life prediction results

由圖17可知,基于數據擴增和BLSTM預測的剩余壽命結果能夠不斷收斂于真實剩余壽命,其預測精度高于另外3類方法的預測精度。

為了表明本文所提方法的泛化性,預測不同工況下的軸承剩余壽命,并其他方法進行對比分析。為了便于對比,統一采用累積相對精度(cumulative relative accuracy,CRA)評估預測結果。CRA的計算公式如下:

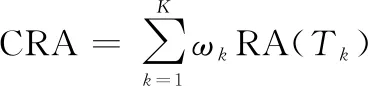
(22)

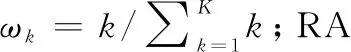
(23)

由累積相對精度的計算公式可知,累積相對精度越大,表明預測結果越好。不同方法的預測結果如圖18所示。其中,橫坐標中的數字表示第類工況下的第個軸承。例如,11表示第1類工況下的第一個軸承,以此類推。

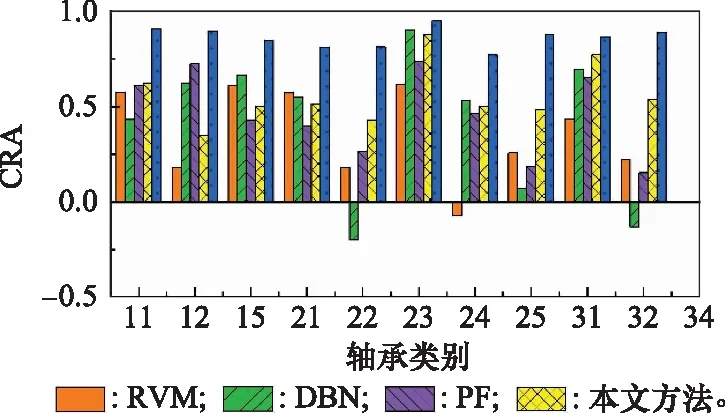
圖18 不同方法的CRAFig.18 CRA of different methods

由圖18可知,本文所提方法預測不同工況的軸承剩余壽命CRA均高于其他幾類方法,表明該方法具有較好的泛化性。

4 結 論

針對深度學習網絡訓練數據不足的問題,本文提出一種基于時間序列數據擴增和BLSTM的剩余壽命預測方法。在訓練軸承全壽命周期數據的基礎上,利用動態時間規整算法,擴增測試軸承性能退化數據,為BLSTM網絡提供觀測數據,預測滾動軸承性能退化過程,進而預測滾動軸承剩余壽命。實驗結果證明:① 基于動態時間規整算法的數據擴增模型能夠根據已有全壽命周期數據擴增性能退化過程相似的滾動軸承運行數據;② 數據擴增模型能夠為BLSTM網絡提供觀測數據,從而提高網絡預測性能退化趨勢和剩余壽命的精度;③ 相比于傳統數據驅動的剩余壽命預測方法,本文所提方法具有更高的預測精度和泛化性。