基于確信可靠性理論的蠕變壽命模型應用研究

楊 晗, 王浩偉, 李清榮, 陳 敏, 彭 博

(北京航空航天大學云南創新研究院, 云南 昆明 650233)

0 引 言

金屬材料在溫度不變、載荷不變的條件下,隨著時間的增長而產生緩慢塑性變形的現象被稱為蠕變。蠕變可以在任何溫度范圍發生,但對于絕大多數金屬材料而言,常溫下蠕變產生的變形量很小,往往可以忽略不計。但對于航空發動機葉片、工業轉化爐管、主蒸汽管道等在高溫環境下工作的構件,就必須考慮蠕變所產生的變形以及可能由此引發的持久斷裂風險。因此,評估構件在高溫工況下的蠕變可靠壽命可以是保障高溫構件安全正常使用的重要前提。

短時持久試驗的長時蠕變壽命外推法是比較常用的蠕變壽命評估方法,目前常用的包括:經驗關系式外推法、等溫線外推法、時間-溫度參數法等。其中,最早發展的線性外推持久強度法側重蠕變鍛煉機理的研究;此后發展起來的以Larson-Miller法為代表的時間溫度參數法得到最為廣泛的研究和應用;在對時間溫度參數法的研究和豐富中,逐漸發展出來根據蠕變曲線規律進行壽命預測的方法,其中參數法比較受認可。然而此類方法主要是基于大量的實驗基礎,且外推法適用范圍有限,超出范圍后會出現較大的偏差。

隨著可靠性學科的發展,可靠性的相關概念也被應用到蠕變壽命評估中。Evans等人通過對比不同的分布模型,認為12Cr12Mo14V鋼的蠕變失效時間符合對數正態分布。Zhao等人與Kim等人分別使用參數分散性的方法,考慮了材料存在的分散性問題,從可靠性的角度合理計算了材料在一定使用條件下的蠕變斷裂壽命。Zhang等人提出了一種分布式協同廣義回歸極值神經網絡方法,并在此基礎上對某型航空發動機葉尖間隙進行了可靠性分析。但總的來說,對于蠕變可靠壽命的研究,仍然是以大量實驗為依托,然而蠕變持久試驗所需時間較長,在工程實際中通常只能得到有限的樣本數據。此外,這些方法也僅考慮了材料的分散性可能帶來的固有不確定性影響,并未考慮對客觀世界規律認識不足而產生的認知不確定性,以及由工況、環境等因素帶來的不確定性。

為了量化工程應用中廣泛存在的不確定性,國內外學者進行了很多嘗試和研究,其中Liu等人于2007年提出不確定理論,是公理化數學一個新的分支,為解決小樣本問題和認知不確定的問題提供了新的工具,在不同的研究領域中得到應用。在工程實際及蠕變可靠壽命評估中往往很難得到充足的試驗樣本,因此不確定理論可以作為評價蠕變過程不確定性的新手段。

在可靠性建模方面,Kang等人在結合工程實際和深入研究可靠性度量基本準則的基礎上,認為可靠性是確定性和不確定性的綜合,提出了一種新的可靠性理論:確信可靠性理論。并定義確信可靠度為在認識確定性規律基礎上量化不確定性得到的可靠度。確信可靠性理論以不確定理論和概率論為基礎。于格等人基于確信可靠性理論對齒輪的接觸疲勞可靠壽命進行了研究,考慮了認知不確定性,并通過分析找到了齒輪接觸疲勞的敏感參數。王浩偉等人基于不確定理論對退化數據進行分析,并利用時變不確定正態分布建立產品的退化方程,最終根據度量方程推導出產品可靠性模型。使用不確定統計中的極大似然估計法與假設檢驗法解決參數估計與模型驗證問題。Zu等人使用基于不確定理論用小樣本疲勞試驗數據建模和估計疲勞壽命的不確定性。Li等人基于不確定理論和確信可靠性理論建立了疲勞裂紋擴展可靠壽命模型,并通過分析認為不確定理論能在考慮認知不確定時可以得到更穩定的可靠性評價結果,并發現材料的分散性對疲勞壽命有顯著影響影響。可見,確信可靠性理論為可靠性建模提供了新的思路,并在退化損傷與可靠壽命建模方面有了一定的研究與應用基礎。

綜上,現有的蠕變壽命預測和可靠壽命建模方法,多需要以大量實驗數據為基礎,且難以同時考慮材料分散性、工況和環境的波動性以及認知不確定性。基于不確定理論的方法建立確信可靠性模型適用于工程實際中的小樣本情況,并能充分考慮存在的固有不確定性和認知不確定性的影響。因此,本文將基于確信可靠性這一新理論,使用不確定理論的方法,建立蠕變確信可靠性壽命模型,為蠕變壽命的評估和預計提供一種新的思路與方法。

1 相關理論基礎

本節對本文工作的理論基礎進行介紹,包括不確定理論與確信可靠性理論的重要定義與定理。

1.1 不確定理論

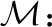
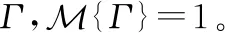
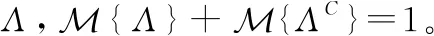
次可加公理:對于一列可數的事件序列,,…

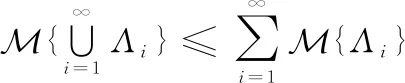
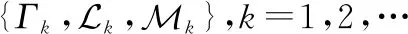
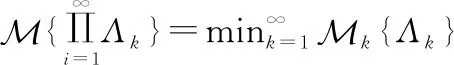
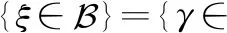
是一個事件,則稱是一個不確定變量。

不確定分布:設是一個不確定變量,則函數

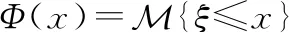
稱為的不確定分布。

逆不確定分布:令表示一個具有正則不確定分布()的不確定變量,則將()的反函數()稱作的逆不確定分布。

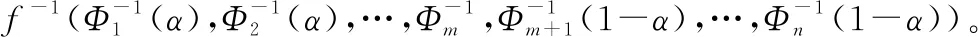
1.2 確信可靠性理論

確信可靠性理論遵循可靠性科學最基本的3個原理:裕量可靠原理、退化永恒原理、不確定原理。對于這3個原理,可以用以下3個方程來表示。

(1) 裕量方程:=(,)>0。

(2) 退化方程:=(,,,)。

(3) 度量方程:()=(>0)。

其中,裕量方程對應裕量可靠原理,描述客體性能裕量的大小和故障判據,即裕量本質上是性能特性到性能閾值的距離,裕量大于0 則產品可靠。退化方程對應退化永恒原理,客體的性能與系統的內在屬性、外在屬性、物理時間沿著退化時矢發生不可逆的退化的規律,退化方程描述了產品確定性的退化規律。度量方程對應不確定原理,描述了對于裕量方程中不確定性的量化,并據此給出產品的可靠度。由此可以認為確信可靠度是在認識確定性規律基礎上量化不確定性得到的可靠度。

2 蠕變過程的確信可靠性建模

本節將基于確信可靠度和不確定理論進行蠕變壽命的可靠性建模,包括基于確信可靠理論的建模過程和基于不確定理論的參數不確定性表征。

2.1 確信可靠性理論

高溫下構件的蠕變變形量和時間的關系曲線稱為蠕變曲線,如圖1所示,可以看出蠕變分為3個階段。

(1) 第Ⅰ階段:蠕變變形速率隨時間呈下降趨勢;

(2) 第Ⅱ階段:蠕變變形速率時間保持恒定;

(3) 第Ⅲ階段:蠕變變形速率隨時間呈上升趨勢,至構件破壞。

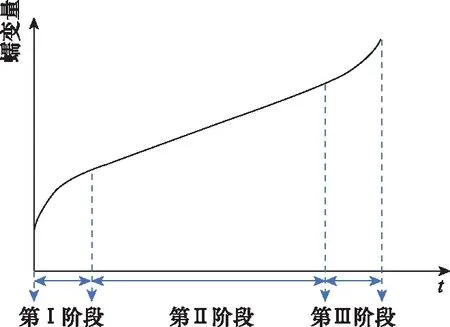
圖1 蠕變曲線Fig.1 Creep curve

一般情況下,第Ⅰ階段及第Ⅲ階段相較于第Ⅱ階段持續時間較短,某些情況下甚至不出現第三階段。因此,為簡化建模過程,只考慮第Ⅱ階段的蠕變變形過程,即認為蠕變變形速率隨時間保持恒定。此外,對于大多數金屬結構件來說,施加載荷瞬間產生的彈性變形相較于蠕變變形很小,且為可恢復形變。因此,在建模過程中不考慮施加載荷瞬間產生的彈性形變。

基于以上假設和簡化處理,使用確信可靠性理論建立蠕變壽命模型。

蠕變速率受很多因素影響,可以表示為

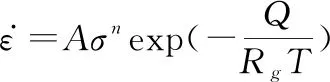
(1)

在式(1)的基礎上,選擇蠕變變形量為蠕變過程的關鍵性能參數。按照故障閾值對性能參數的限定形式,可以將性能參數分為3類:

(1) 望小性能參數:當且僅當≥時,產品發生故障;

(2) 望大性能參數:當且僅當≤時,產品發生故障;

(3) 望目性能參數:當且僅當≤th,或≥th,時,產品發生故障。

由此,裕量方程可構建為如下的形式:

(2)

關鍵點斷裂應變理論認為,當結構內部任意位置蠕變應變累積超過某一臨界值時,結構發生持久斷裂失效。因此,可以將蠕變累積應變量到達某一臨界值作為蠕變失效的判斷條件,且蠕變變形量為望小性能參數,由此構建裕量方程,其中為蠕變變形量失效閾值:

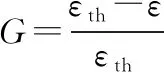
(3)

蠕變變形量隨時間變化,可根據式(1)建立隨時間的退化方程:

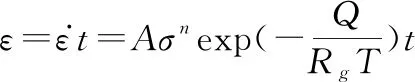
(4)

當裕量≥0時認為是可靠的,因此可以建立可靠度方程:

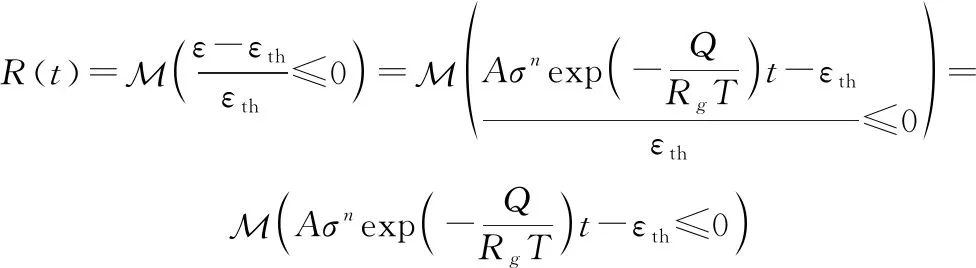
(5)

2.2 參數不確定性表征

確信可靠度建模需要對不確定性進行量化,因此在得到確定性的式(5)后還需要進一步討論下式參數可能存在的不確定性：

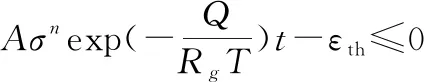
(6)

參數不確定性可能有兩種情況:固有不確定性和認知不確定性。固有不確定性的實質是客體世界內在的不確定性,又可以稱為是隨機不確定性。認知不確定性是由于人的認知能力的有限性而產生對客觀規律認識的局限而造成的。由于材料的分散性、工況和環境的波動性、認知的不完備等造成了式(6)中的參數具有固有不確定性與認知不確定性的情況。因此,將式(6)中的參數根據其不確定性進行分類。

對于固有不確定性參數,其不確定性的來源主要為外加應力、工作環境溫度以及材料性能的分散性。對于認知不確定性參數,其不確定性主要來源于對客觀規律認知的不充分,即目前對于蠕變的機理與規律的研究和認知并不完全。常數()的認知不確定性主要來源于對材料、蠕變規律認知的不充分;蠕變應力指數()的認知不確定性主要來源于對蠕變機理認知的不充分;蠕變激活能()的認知不確定性主要來源于對材料性能、蠕變機理認知的不充分。具體參數滿足分布如表1所示,參數所滿足的不確定分布主要由經驗進行,和已有的數據規律進行選擇。

表1 參數不確定性分布情況

(1) 存在固有不確定性的參數:外加應力(),溫度(),蠕變變形量失效閾值();

(2) 存在認知不確定性的參數:常數(),蠕變應力指數(),蠕變激活能();

(3) 確定性參數:氣體常數()。

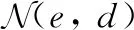
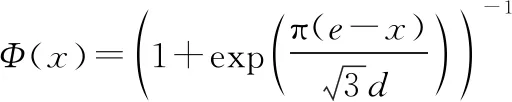
(7)

考慮所有參數的不確定性時,根據定理1(運算法則)可以將式(5)表達為

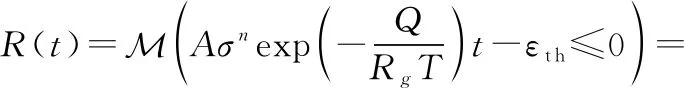
(8)

其中,不確定正態分布的逆不確定分布為

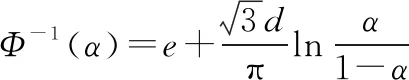
(9)

由式(8)可見,該過程需要考慮不確定性的參數較多,可根據情況進行簡化。

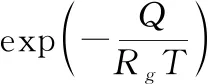
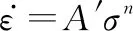
(10)

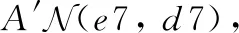
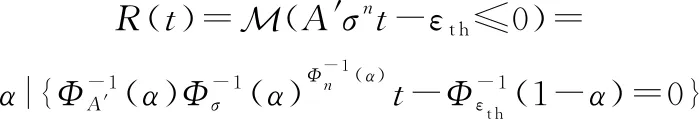
(11)

2.3 分布參數的獲得

在工程實踐中,往往很難通過大量蠕變持試驗獲得分布參數。確信可靠性理論中,除了可以通過少量實驗數據進行不確定參數估計以外,還可以通過專家和經驗進行分布參數的確定,更適用于工程實際情況,且能充分利用專家和經驗的資源。因此,不同的參數分布中的未知參數可通過不確定估計、經驗確定及專家指定獲得。

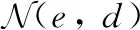
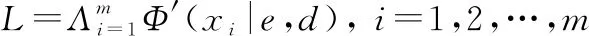
(12)

式中:符號為取小之意,且,

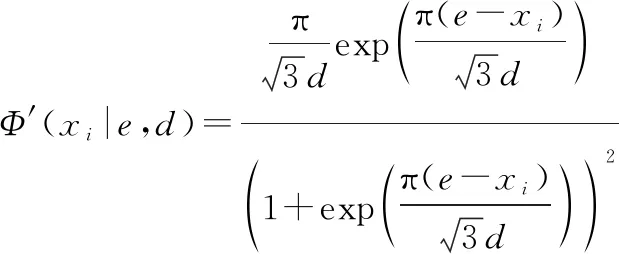
(13)

在沒有試驗和測量數據的情況下,還可以通過工程經驗和專家指定的方式確定未知參數。

2.4 參數不確定性優化分析

在確信可靠模型建立完成后,還需要對參數不確定性的考慮進行優化分析。本文提出一種以失效時間模型為參照的參數不確定性優化與分析方法。

將得到的蠕變確信可靠模型與基于失效時間數據的概率分布建模進行比較,并考慮不同參數不確定性的影響。通過面積比的方法比較,優化選擇最合適的參數不確定性表征,并最終得到更合理的蠕變確信可靠模型。

3 案例研究

某牌號Cr-Mo鋼在550 ℃下的蠕變試驗數據如表2所示,該類鋼常用于超高壓機組螺栓與閥門,為典型金屬材料。

表2 某牌號Cr-Mo鋼蠕變試驗數據(550 ℃)

3.1 分布參數及可靠度曲線

可將式(10)改寫為對數形式為

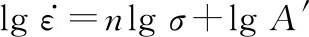
(14)

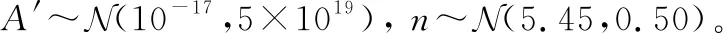
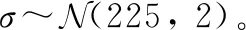
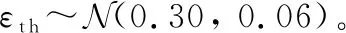
表3 失效應變量統計

各分布參數及獲取方式如表4所示,根據式(9)和式(11)可計算得到此牌號Cr-Mo鋼材料在該條件下的可靠度隨時間變化的曲線,如圖2所示,并通過曲線可得到其可靠壽命:09=481 h,06=9 727 h。可靠度在早期隨時間下降迅速,且下降速率隨時間逐漸降低,中后期可靠度隨時間下降趨勢較為平緩。

表4 分布參數及確定方式

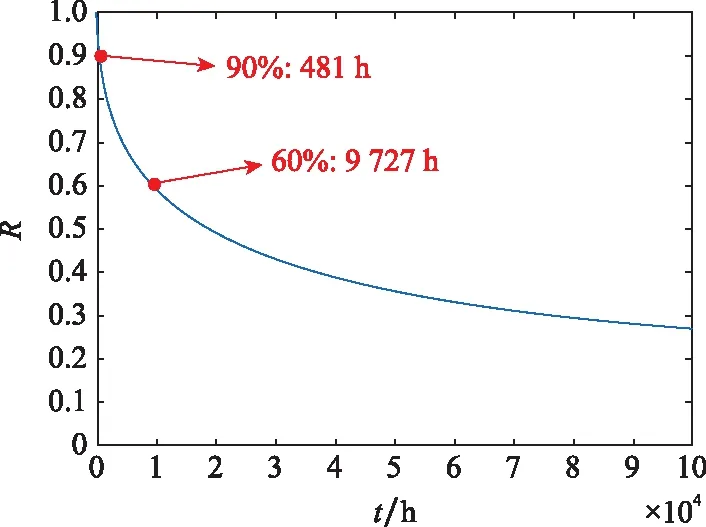
圖2 某牌號Cr-Mo鋼考慮四參數不確定性條件下可靠度隨時間變化曲線Fig.2 Reliability versus time curve of a certain brand of Cr-Mo steel considering four parameter uncertainties

3.2 參數不確定性影響

不同參數的不確定性對可靠壽命曲線影響不同,因此依次考慮表4中參數的不確定性,在此基礎上研究不同參數不確定性對可靠度曲線的影響。在考慮某一參數不確定性時,認為其余參數均為確定參數,取值為分布參數。

圖3所示為分別考慮不同參數不確定性的情況下所計算得到的可靠度隨時間變化曲線。可以發現,僅考慮的不確定性時所得曲線與同時考慮四參數時所得曲線最類似,說明參數的不確定性對可靠壽命的影響最為顯著,甚至掩蓋了另外3個參數的影響。由于參數不確定性的影響,蠕變確信可靠度在早期就迅速下降,而中后期確信可靠度下降曲線則趨于平緩。因此對于蠕變過程來說,需要重點控制參數的不確定性。參數與蠕變機理有關,而蠕變機理又與材料、載荷和對蠕變機理的認知水平有關,因此可以控制材料的分散性和工況的波動性以減少參數的不確定性,以減小可靠度曲線早起的下降趨勢,增加可靠壽命。

圖3 某牌號Cr-Mo鋼分別考慮單參數不確定性的可靠度隨時間變化曲線Fig.3 Reliability versus time curves of a certain brand of Cr-Mo steel with single parameter uncertainty

3.3 參數不確定性優化與分析

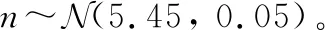
表5為一種Cr-Mo鋼(12Cr12Mo14V)在173 MPa/550 ℃條件下的失效時間數據,認為其失效時間滿足對數正態分布。某Cr-Mo鋼減小參數不確定性后確信可靠度隨曲線與12Cr12Mo14V鋼基于失效時間的可靠度曲線如圖4所示。其中,藍色實線為減小參數不確定性后的蠕變確信可靠度曲線,根據曲線得到的蠕變可靠壽命:=8 213 h,=16 390 h。對比圖2可發現在減小的不確定性以后,早期可靠度不再出現明顯的下降,可靠壽命也得到顯著的提高。

表5 12Cr12Mo14V蠕變失效時間數據(173 MPa/550 ℃)

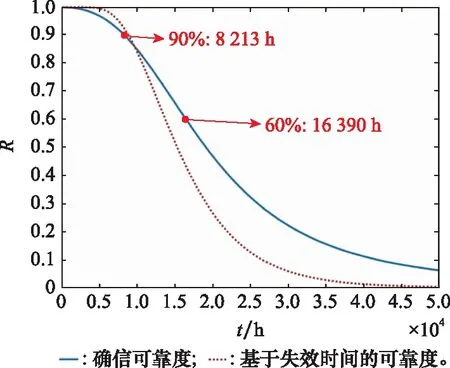
圖4 某Cr-Mo鋼減小n不確定性后確信可靠度隨時間變化曲線與12Cr12Mo14V鋼基于失效時間的可靠度曲線Fig.4 Reliability versus time curve of certain Cr-Mo steel with reduced uncertainty of n and reliability curve of 12Cr12Mo14V steel based on failure time

此外,由圖4可以觀察到,優化參數不確定性后的確信可靠度曲線與通過失效時間得到的可靠度曲線有著類似的變化趨勢,這說明此時得到的蠕變確信可靠度模型所得到的結果與慣常使用的基于失效數據的概率可靠度模型得到的結果有一定程度上的一致性。在早期的高可靠度階段,二者相差較小,且基于確信可靠性理論得到的結果相對保守;而在中后期,則是基于失效時間數據得到的可靠度相對基于確信可靠性理論得到的結果更為保守。造成這種差異的主要原因是參數的對蠕變確信可靠度的影響,使得可靠度在早期下降快,在中后期下降趨于平緩。

為了進一步討論參數不確定性的影響,可以考慮極端情況,即不考慮參數的不確定性,將其取確定值為545,其余3個參數的分布不變,則式(11)可寫為

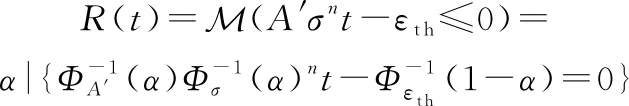
(15)

結合式(9)和式(15)計算得到蠕變確信可靠度曲線,將得到的可靠度曲線與失效基于失效時間數據的曲線進行對比,如圖5所示,并可獲得蠕變可靠壽命:09=11 260 h,06=17 360 h。

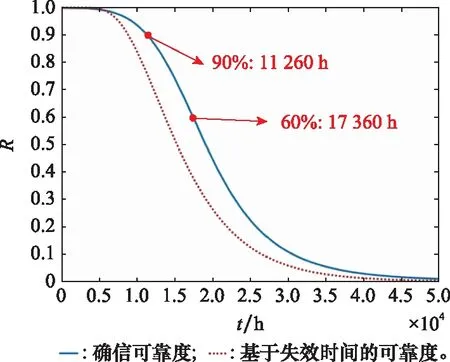
圖5 某Cr-Mo鋼不考慮n不確定性條件下確信可靠度隨時間變化曲線與12Cr12Mo14V鋼基于失效時間的可靠度曲線Fig.5 Reliability versus time curve of certain Cr-Mo steel without considering uncertainty of n and reliability curve based on failure time for 12Cr12Mo14V steel

在不考慮的不確定性后,早期可靠度不再明顯下降,因此高可靠度下的可靠壽命相較于考慮參數不確定性的情況下有所提高。此時,蠕變的確信可靠度曲線與基于失效時間的可靠度曲線趨勢更為相似,在整個過程中基于失效時間的可靠度結果都相對保守。這也進一步說明,參數在很大程度上影響了蠕變確信可靠度曲線的變化趨勢,從而影響其可靠壽命模型的結果,最主要影響的是早期的可靠度變化趨勢。

將基于失效時間數據的模型作為參照,采用面積比的方法分別表征圖4和圖5中基于確信可靠理論的可靠度曲線與基于失效時間數據的可靠度曲線的相抵度。具體方法為:計算兩條曲線所圍面積和兩條曲線與坐標軸所圍面積的比值,如圖6所示。因此,面積比計算公式為

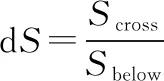
(16)

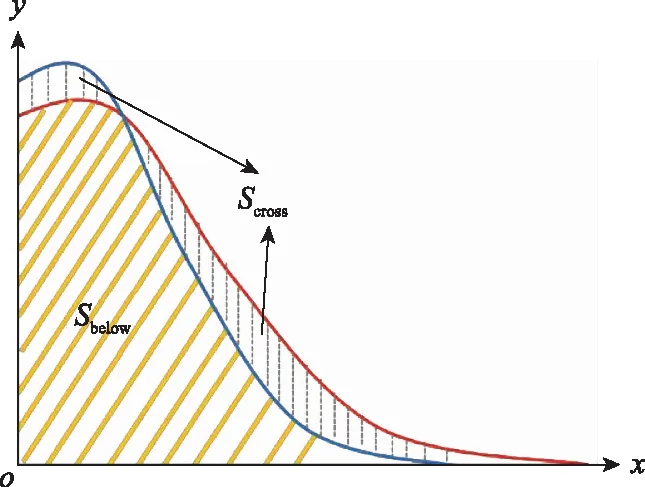
圖6 面積比法所求面積示意圖Fig.6 Schematic diagram of area ratio method

由此分別計算原文圖4與圖5中兩條曲線的面積比分別為0.278和0.067 5。即圖5中兩條曲線的相似性更好。說明在不考慮參數不確定性的情況下,確信可靠模型與基于失效時間數據的概率統計模型有很好的相似度。

在案例中,基于確信可靠性理論和不確定理論進行了蠕變可靠性建模,得到蠕變的確信可靠度曲線。該方法使用不確定理論及運算法則,可以方便簡單地考慮多個參數不確定性影響。此外,參數的分布可以通過多種方式獲取,即除了通過試驗、參數估計等常規使用的方法外,還可以通過經驗和專家指定等較為主觀的方法。使用該方法建模可以得到與工程實踐中廣泛使用的基于失效時間的概率統計方法得到的可靠度模型較為一致的結果,從而給難以開展蠕變試驗、缺乏蠕變試驗數據、蠕變試驗成本較高等情況提供了蠕變壽命建模方法,具有工程實用價值。

4 結 論

本文基于確信可靠性理論為蠕變壽命建模提供新方法,該方法可以通過使用不確定理論的運算法則同時充分考慮材料分散性、載荷波動性、溫度波動性、認知不完全性等帶來的不確定性,相比較使用概率方法有計算簡單易行的優勢。

基于確信可靠性理論的蠕變可靠性壽命建模方法在使用中可以通過試驗數據參數估計、經驗確定和專家指定等多種方法獲得參數分布,在缺少試驗數據和試驗難以進行的情況下提供了蠕變可靠壽命評估的手段,具有較好的工程應用價值。

不同參數的不確定性對可靠度曲線的影響程度不同,在蠕變過程中,蠕變應力指數的不確定性對所得可靠度曲線影響最大,需要重點關注,在對參數不確定性的進行調整和控制以后,可以得到與基于失效時間數據的概率分布模型方法得出的類似的建模計算結果。

在建模方法上,目前的局限主要在未考慮參數間的相關性,未來的研究中可以從參數間的影響因素和其相關性出發,去修正已有的確信可靠度模型,使得模型更完備。在應用層面,本文僅考慮蠕變這一單一的失效模式,未考慮復合失效模式的作用,未來的研究可以針對蠕變-疲勞、蠕變-腐蝕等多種失效模式共同作用的情況開展研究。