基于指派模型的導(dǎo)彈裝備體系彈種優(yōu)化設(shè)計

郭斐然, 于劍橋, 宋 豹

(北京理工大學(xué)宇航學(xué)院, 北京 100081)

0 引 言

隨著武器裝備技術(shù)的迅猛發(fā)展,面向未來信息化條件下聯(lián)合作戰(zhàn)的軍事需求,組成裝備體系的各武器系統(tǒng)需在一定的能力條件下協(xié)同作戰(zhàn),從而最大程度發(fā)揮裝備體系的效能[1]。針對導(dǎo)彈裝備體系而言,包含多彈種的彈族化設(shè)計需要按照系統(tǒng)工程的方法, 從頂層需求出發(fā), 優(yōu)化確定彈族中各彈種的戰(zhàn)術(shù)技術(shù)指標(biāo)和基本設(shè)計方案,是導(dǎo)彈裝備體系設(shè)計方法的新發(fā)展。在已有的采用彈族化思想設(shè)計或改進的導(dǎo)彈中,“阿斯特”防空導(dǎo)彈族是較為典型的代表。“阿斯特”導(dǎo)彈族各系統(tǒng)、型號采用相同的設(shè)計概念,具有模塊化結(jié)構(gòu)設(shè)計、部件通用性高、后續(xù)發(fā)展?jié)摿Υ笠约白鲬?zhàn)和維護自動化程度高等特點。此外,美國的“標(biāo)準(zhǔn)”艦空導(dǎo)彈系列、俄羅斯C-300B(SA-12)的防空導(dǎo)彈系列等均在一定程度上采用了彈族化設(shè)計思想[2]。關(guān)于彈族化設(shè)計的研究,邢恩峰等進行了面向大規(guī)模定制的彈藥模塊化設(shè)計及產(chǎn)品族規(guī)劃研究[3],仝云對防空導(dǎo)彈彈族進行了多目標(biāo)優(yōu)化設(shè)計研究[4],孫曉峰提出了戰(zhàn)斗部質(zhì)量不同情況下組成中近程防空導(dǎo)彈與中遠程防空導(dǎo)彈彈族的設(shè)計流程[5]。這些研究均關(guān)注了針對某一類型任務(wù)需求的單一彈種的彈族化設(shè)計,而對滿足不同類型任務(wù)需求的多彈種優(yōu)化設(shè)計的研究仍不多見。相比于單型導(dǎo)彈的優(yōu)化設(shè)計,包含多彈種的彈族化設(shè)計具有體系結(jié)構(gòu)復(fù)雜、任務(wù)需求廣泛、優(yōu)化變量數(shù)目龐大的特點,為提高設(shè)計效率、降低設(shè)計成本,本文針對體系作戰(zhàn)中多彈種協(xié)同完成多類型作戰(zhàn)任務(wù)的需求,在體系設(shè)計中引入若干通用設(shè)計模塊,并在設(shè)計過程中采用優(yōu)化方法,加快設(shè)計過程。

類似于現(xiàn)實生活中為若干人員分配若干項工作任務(wù),在滿足特定的指派要求條件下,使指派方案總體效果最佳,武器系統(tǒng)優(yōu)化設(shè)計模型也可抽象為相應(yīng)的指派模型,在滿足一定的約束條件下進行計算求解。目前,指派問題應(yīng)用的領(lǐng)域中絕大多數(shù)為經(jīng)濟民生領(lǐng)域,如工業(yè)生產(chǎn)[6]、交通出行[7-8]、物流運輸[9]等,用于分析武器裝備的研究文獻尚不多見,其中張超省等構(gòu)建了一種戰(zhàn)士—裝備—任務(wù)的三維指派模型[10],雖然模型中包含裝備,但研究主體仍為操作裝備的人。葉航航等針對導(dǎo)彈—目標(biāo)的分配問題建立了經(jīng)典的指派問題模型[11],并對分配算法進行了深入研究,但研究范圍過于局限,模型中仍為導(dǎo)彈和目標(biāo)的一一對應(yīng)關(guān)系,未體現(xiàn)出導(dǎo)彈作為子系統(tǒng)與裝備體系的關(guān)系。

對于導(dǎo)彈裝備體系來說,通過不同類型的導(dǎo)彈部件組合成不同的彈種進行優(yōu)化設(shè)計,本質(zhì)上屬于組合優(yōu)化問題。組合選擇理論由Markowitz最早提出[12],Buede等[13]最早進行了基于多目標(biāo)規(guī)劃的項目組合的研究。Buckshaw等[14]在系統(tǒng)組合分析中運用了專家評分法,Kangaspunta等[15]對組合后系統(tǒng)的連通性進行了評估。此外針對軍事領(lǐng)域,還有不少學(xué)者對武器系統(tǒng)組合方法進行了研究。其中,Kangaspunta等[15]通過對抗模擬確定武器裝備系統(tǒng)組合的價值,提出了價值導(dǎo)向的武器系統(tǒng)組合優(yōu)化方法,周宇提出了基于能力的武器裝備組合規(guī)劃問題與方法[16],張驍雄等提出了面向能力需求的組合優(yōu)化算法[17],進一步強調(diào)了基于能力的思想。在此基礎(chǔ)上,夏博遠等提出了基于動態(tài)能力需求的魯棒性武器系統(tǒng)組合決策[18],錢曉超等研究了基于效能評估的武器裝備體系優(yōu)化設(shè)計方法[19],實現(xiàn)了武器裝備體系設(shè)計的多目標(biāo)優(yōu)化求解,然而這些研究大都圍繞武器裝備的“頂層規(guī)劃”,很少涉及部件層級的優(yōu)化設(shè)計。在武器系統(tǒng)的組合優(yōu)化過程中,目前存在比較困難的問題是隨著武器系統(tǒng)規(guī)模的增大,系統(tǒng)的組合可行解空間會呈現(xiàn)指數(shù)級增長,出現(xiàn)“組合爆炸”的情況,給問題的求解帶來了極大困難。同時,如何限制武器系統(tǒng)的選擇界限、給出更為合理的武器系統(tǒng)組合方案也存在較大問題[20]。

層次分析法(analytic hierarchy process,AHP)是美國運籌學(xué)家Saaty于20世紀(jì)70年代初提出的一種層次權(quán)重決策分析方法,主要用于解決體系結(jié)構(gòu)建模中的權(quán)值確定問題[21]。本文對體系中各個通用設(shè)計模塊按照AHP的思想進行層次分解,確定各模塊下的組成要素,各層組成要素與上一層之間的關(guān)系分別以相應(yīng)的貢獻度表征,貢獻度越大則影響程度越高。在構(gòu)建組合優(yōu)化的數(shù)學(xué)模型過程中,將構(gòu)成彈種的不同類型的部件抽象為“人”,將不同類型的部件對頂層體系效能的絕對貢獻度抽象為完成任務(wù)的“效率”,進而以綜合考慮任務(wù)、成本和風(fēng)險影響因素的裝備體系效能最優(yōu)為目標(biāo)構(gòu)建指派模型,并給出相應(yīng)的約束條件。在對模型進行優(yōu)化求解時引入作戰(zhàn)環(huán),將不同類型的導(dǎo)彈部件組合為整體的彈種對模型優(yōu)化求解,使得優(yōu)化問題的可行解空間極大縮小,同時明確了彈種入選最優(yōu)組合方案的“邊界”,提高了計算求解的效率,期望為導(dǎo)彈裝備體系的彈種組合優(yōu)化設(shè)計提供一種嶄新且有效的思路。

1 彈種優(yōu)化設(shè)計層次結(jié)構(gòu)模型建立

為更好進行導(dǎo)彈裝備體系多彈種的彈族化設(shè)計,提高設(shè)計效率、降低設(shè)計成本,引入若干通用設(shè)計模塊表征導(dǎo)彈裝備體系彈種優(yōu)化設(shè)計結(jié)構(gòu)模型。如圖1所示,建立以體系效能為引導(dǎo)的包含通用設(shè)計模塊的彈種優(yōu)化設(shè)計結(jié)構(gòu)模型。其中,在任務(wù)性能中包含任務(wù)需求、能力需求和任務(wù)指標(biāo)3個設(shè)計模塊;在成本性能中包含任務(wù)成本、成本指標(biāo)和部件成本3個設(shè)計模塊,均對應(yīng)到部件模塊,進而通過部件模塊的優(yōu)化設(shè)計得到最優(yōu)的彈種組合方案,完成導(dǎo)彈裝備體系的多彈種優(yōu)化設(shè)計。

根據(jù)AHP的思想,對模塊化設(shè)計結(jié)構(gòu)模型中的各個通用設(shè)計模塊進行層次分解,為后面建立具體的優(yōu)化模型奠定基礎(chǔ)。裝備體系效能引導(dǎo)的彈種優(yōu)化設(shè)計模型層次結(jié)構(gòu)依次可分為目標(biāo)層、子目標(biāo)層、成本層、任務(wù)成本層、指標(biāo)成本層、部件成本層、部件層和導(dǎo)彈種類層,相應(yīng)的層次結(jié)構(gòu)和各層組成要素如圖2所示。目標(biāo)層為裝備體系效能,由任務(wù)性能和經(jīng)濟性能綜合表征。其中任務(wù)性能由具體的精確壓制任務(wù)能力、精確打擊任務(wù)能力、高精度點打擊任務(wù)能力、巡飛察打評能力、防空能力等綜合決定,經(jīng)濟性能由生產(chǎn)制造成本、使用成本等綜合決定,且生產(chǎn)制造成本在裝備體系中由完成任務(wù)相應(yīng)的精確壓制任務(wù)成本、精確打擊任務(wù)成本、高精度點打擊任務(wù)成本、巡飛察打評任務(wù)成本、防空任務(wù)成本等共同決定。確定裝備體系完成相應(yīng)任務(wù)的能力需要建立相應(yīng)的任務(wù)指標(biāo),因此在任務(wù)層的下一層級建立相應(yīng)的指標(biāo)層,對應(yīng)于任務(wù)能力的任務(wù)指標(biāo)層元素有精度指標(biāo)、射程指標(biāo)、威力指標(biāo)等,且精度指標(biāo)、射程指標(biāo)和威力指標(biāo)等共同影響精確壓制任務(wù)能力、精確打擊任務(wù)能力、高精度點打擊任務(wù)能力、巡飛察打評能力和防空能力。對應(yīng)于任務(wù)成本的任務(wù)成本指標(biāo)層元素有精度成本指標(biāo)、射程成本指標(biāo)、威力成本指標(biāo)等,且精度成本指標(biāo)、射程成本指標(biāo)和威力成本指標(biāo)共同影響裝備體系精確壓制任務(wù)成本、精確打擊任務(wù)成本、高精度點打擊任務(wù)成本、巡飛察打評任務(wù)成本和防空任務(wù)成本。對于不同種類的導(dǎo)彈例如衛(wèi)星制導(dǎo)導(dǎo)彈、激光半主動制導(dǎo)導(dǎo)彈、激光駕束制導(dǎo)導(dǎo)彈、慣性制導(dǎo)導(dǎo)彈、無控導(dǎo)彈、巡飛導(dǎo)彈、防空導(dǎo)彈等,彈上部件可大體分為導(dǎo)引頭、慣性測量單元(inertial measurement unit,IMU)、舵機、發(fā)動機以及戰(zhàn)斗部等,其中導(dǎo)引頭包括:① 捷聯(lián)主動尋的導(dǎo)引頭;② 捷聯(lián)半主動尋的導(dǎo)引頭;③ 平臺主動導(dǎo)引頭;④ 平臺半主動導(dǎo)引頭等。IMU包括:① 導(dǎo)航用IMU;② 控制用IMU等。舵機包括:① 單通道舵機;② 雙通道舵機;③ 三通道舵機等。發(fā)動機包括:① 超口徑高能量增程發(fā)動機;② 超口徑低特征信號增程發(fā)動機;③ 同口徑增速發(fā)動機等。戰(zhàn)斗部包括:① 聚能破甲戰(zhàn)斗部;② 攻堅戰(zhàn)斗部;③ 爆破殺傷戰(zhàn)斗部等。各種類導(dǎo)彈均可安裝相應(yīng)的部件滿足不同任務(wù)需求。導(dǎo)引頭部件和IMU影響裝備體系的精度指標(biāo),且通過相應(yīng)的組成單元成本影響精度成本指標(biāo);舵機影響裝備體系的精度指標(biāo)和射程指標(biāo),且通過相應(yīng)的組成單元成本影響精度成本指標(biāo)和射程成本指標(biāo);發(fā)動機影響裝備體系的射程指標(biāo),且通過相應(yīng)的組成單元成本影響射程成本指標(biāo);戰(zhàn)斗部影響裝備體系的威力指標(biāo),且通過相應(yīng)的組成單元成本影響威力成本指標(biāo)。各層的組成要素與相鄰層次間的組成要素的相關(guān)關(guān)系可用連線加以表示,由于劃分的層次中處于同一層的各組成要素特性不同,對上一層要素的影響程度也不盡相同,因此在建立優(yōu)化模型進行優(yōu)化設(shè)計的過程中需依次確定各層的組成要素分別對上一層要素的影響程度,也即該要素對上層相關(guān)要素的貢獻度。

為更好地描述裝備體系模型中各層要素之間的關(guān)系,引入效能域、任務(wù)域、成本域、方案域、參數(shù)域和信息域,其關(guān)系如圖3所示,其中參數(shù)域和信息域不顯含于層次結(jié)構(gòu)圖當(dāng)中。效能域包含根據(jù)效能分析模型得到的裝備體系的一系列效能值,是整個優(yōu)化設(shè)計問題的目標(biāo)函數(shù),指導(dǎo)整體的彈種及使用部件方案的設(shè)計,處于最頂層。任務(wù)域包含根據(jù)假想目標(biāo)特點和作戰(zhàn)需求的不同而需要完成的各種不同任務(wù),為效能域提供總體的指標(biāo)方案并為彈種及部件設(shè)計提供直接的參考標(biāo)準(zhǔn)。方案域包含根據(jù)作戰(zhàn)任務(wù)的不同而確定的不同導(dǎo)彈種類和部件組合的有效設(shè)計方案,是整體優(yōu)化問題的可行域。參數(shù)域包含各層級指標(biāo)之間的影響關(guān)系,例如通過專家打分法確定的各層組成要素分別對上一層要素的影響程度,也即貢獻度,參數(shù)域直接影響整體效能函數(shù)的構(gòu)建,進而影響整體設(shè)計方案是否與實際情況相吻合。成本域包含裝備體系中各部件的成本信息,與所用的系統(tǒng)部件數(shù)量成負相關(guān),成本域相關(guān)信息的引入使得系統(tǒng)效能可能存在最優(yōu)解。信息域包含已知的作戰(zhàn)需求信息、假想目標(biāo)集群特性信息等,為系統(tǒng)進行任務(wù)域劃分以及參數(shù)域幅值提供直接依據(jù),是整個優(yōu)化問題構(gòu)建的前提與基礎(chǔ)。圖3中黑色箭頭表示依據(jù)作戰(zhàn)需求計算裝備體系效能的過程中各域之間的層級關(guān)系。

2 指派模型建立

經(jīng)典的指派問題是將不同的任務(wù)分派給若干人去完成,由于每個人完成各項任務(wù)的效率或所需費用不同,因此應(yīng)分派何人去完成哪種任務(wù)使得總效率最高或所需總費用最低是指派模型需要解決的問題。對于本文的彈種優(yōu)化設(shè)計來說,在確定最優(yōu)的彈種組合前需要對組成彈種的不同類型的部件及其性能參數(shù)進行優(yōu)化設(shè)計。根據(jù)第1節(jié)建立的彈種優(yōu)化設(shè)計層次結(jié)構(gòu)模型,可將不同性能參數(shù)的各類部件分別看做需要完成不同任務(wù)的“人”,將不同性能參數(shù)的各類部件對頂層裝備體系效能的絕對貢獻度分別看做完成不同任務(wù)的“效率”,以此為基礎(chǔ)可構(gòu)建相應(yīng)的指派模型。

對于本文的裝備體系結(jié)構(gòu),分別以一些離散的參數(shù)值來表征不同類型部件的不同屬性,同時不同的參數(shù)值對部件的屬性影響不同,從而對整個裝備體系效能的貢獻度也不同。對于代表截獲、跟蹤對方目標(biāo)的核心部件,即導(dǎo)引頭,以有效作用距離來表征其屬性;對于代表測量導(dǎo)彈位置、姿態(tài)等信息的核心部件,即IMU,以姿態(tài)精度和位置精度來表征其屬性;對于代表根據(jù)導(dǎo)引信息操縱導(dǎo)彈運動的核心部件,即舵機,以最大舵偏角和最大舵偏角速度來表征其屬性;對于代表為導(dǎo)彈提供動力的核心部件,即發(fā)動機,以推力和總沖來表征其屬性;對于代表執(zhí)行作戰(zhàn)過程中火力打擊任務(wù)的核心部件,即戰(zhàn)斗部,以質(zhì)量來表征其屬性。

由于指派問題本質(zhì)上屬于0～1整數(shù)規(guī)劃問題[22],因此需要定義該優(yōu)化問題的決策變量如下:

(1)

式中:若選取部件類型j中屬于第k種屬性的第m個參數(shù)值的部件i,則xijkm=1;否則xijkm=0。

按照第1節(jié)建立的彈種優(yōu)化設(shè)計層次結(jié)構(gòu)模型,該優(yōu)化問題需要滿足如下約束條件。

約束 1每個部件只能屬于5種類型部件其中之一,即

(2)

約束 2每種類型部件中至多有一個部件入選,即

(3)

不同性能參數(shù)值的各類型部件對裝備體系效能絕對貢獻度之和表征了裝備體系的綜合效能,優(yōu)化目標(biāo)即找到若干組決策變量的組合,使得裝備體系效能最大。目標(biāo)函數(shù)可表述為

(4)

式中:cijkm為不同性能參數(shù)值的各類型部件對裝備體系效能的絕對貢獻度;k和m的取值范圍視每類部件具體性能屬性的種類和待選取的參數(shù)值數(shù)量而定。

綜上所述,該優(yōu)化問題的指派模型建立如下:

(5)

3 基于作戰(zhàn)環(huán)的快速求解方法

目前求解指派問題應(yīng)用最廣泛的方法是匈牙利法,由美國數(shù)學(xué)家?guī)於骼眯傺览麛?shù)學(xué)家康尼格的關(guān)于矩陣中獨立“0”元素的定理提出[23-24]。匈牙利法對于求解效率矩陣較簡單,對解空間較小的指派問題比較方便實用[25]。然而,隨著決策變量數(shù)量的增加,指派問題的解空間將以2的指數(shù)次方形式增長,匈牙利法的操作過程將變得極其復(fù)雜,且計算耗時巨大,難以被工程應(yīng)用接受。割平面法和分支定界法也同樣是實踐中求解指派問題的經(jīng)典方法。1958年,美國應(yīng)用數(shù)學(xué)家Ralph首先提出用割平面法求解整數(shù)線性規(guī)劃問題,然而該方法比較適用于求解規(guī)模較小的整數(shù)線性規(guī)劃問題,且該方法的收斂速度比較慢[26-27],在解決具有多組最優(yōu)解情形的整數(shù)線性規(guī)劃問題時會造成遺忘解的存在,不能有效尋找到所有的最優(yōu)解[28]。20世紀(jì)60年代,美國科學(xué)家Richard提出了求解整數(shù)線性規(guī)劃問題的另一種方法,即分支定界法[29]。用分支定界法求解整數(shù)線性規(guī)劃問題時平均收斂速度往往比割平面法快,但新增的分支顯然也大幅增加了計算的復(fù)雜度和求解時間[27],因此需設(shè)計能夠大幅減少計算耗時的快速求解方法。

為了將不同類型的導(dǎo)彈部件組合為整體的彈種對模型進行優(yōu)化求解,從而縮小該優(yōu)化問題的可行域、實現(xiàn)快速求解,引入作戰(zhàn)環(huán)理念,并在經(jīng)典作戰(zhàn)環(huán)的基礎(chǔ)上對構(gòu)成作戰(zhàn)環(huán)的元功能節(jié)點加以改進,使其更符合本文所建立的彈種優(yōu)化設(shè)計層次結(jié)構(gòu)模型。

在2004年,美國學(xué)者Cares[30]運用復(fù)雜網(wǎng)絡(luò)理論建立了信息時代的交戰(zhàn)模型,根據(jù)戰(zhàn)場中各兵種扮演角色不同,把戰(zhàn)場中的兵力節(jié)點分為決策節(jié)點(D)、傳感器節(jié)點(S)、響應(yīng)節(jié)點(I)和目標(biāo)節(jié)點(T)4類,然后根據(jù)節(jié)點之間的關(guān)系建立網(wǎng)絡(luò),并運用網(wǎng)絡(luò)知識進行分析。Cares最先提出了作戰(zhàn)環(huán)的概念,不過沒有給出具體的定義,只是宏觀描述了作戰(zhàn)網(wǎng)絡(luò),缺乏微觀行為的描述,但提出的4類節(jié)點,對武器裝備體系的網(wǎng)絡(luò)化建模中節(jié)點類型的描述研究具有很好的借鑒和參考價值。2012年國防科技大學(xué)的譚躍進教授[31]首次將作戰(zhàn)環(huán)定義為:為了完成特定的作戰(zhàn)任務(wù),武器裝備體系中的偵察類、決策類、攻擊類等武器裝備實體與敵方目標(biāo)實體構(gòu)成的閉合回路,如圖4所示。

通過作戰(zhàn)環(huán)網(wǎng)絡(luò)可以將裝備體系與對方目標(biāo)有機聯(lián)系起來,同時也可以更好體現(xiàn)出不同類型武器裝備間的協(xié)同關(guān)系。類似于武器裝備之間的協(xié)同關(guān)系,構(gòu)成彈種的不同類型部件之間也需要相互協(xié)同。針對本文所提優(yōu)化問題的目標(biāo),即尋找最優(yōu)的部件組合,進而形成最優(yōu)的彈種組合,使裝備體系效能最大,引入作戰(zhàn)環(huán)可以比較方便、快速地對優(yōu)化問題模型進行求解。

首先定義元功能節(jié)點。元功能節(jié)點可以表示為一個三元數(shù)組[32],包含節(jié)點標(biāo)識、節(jié)點類型和節(jié)點風(fēng)險,如下所示:

v=(Identity,Type,Risk)

(6)

式中:Identity代表節(jié)點標(biāo)識,表示元功能節(jié)點在整個裝備體系中的性質(zhì),即任務(wù)性元功能節(jié)點和成本性元功能節(jié)點;Type代表節(jié)點類型,指元功能節(jié)點的分類,從不同的角度可以將元功能節(jié)點分成不同的類型;Risk代表節(jié)點風(fēng)險,即在不同類型部件組成多種不同彈種執(zhí)行相應(yīng)作戰(zhàn)任務(wù)的過程中存在的風(fēng)險,定義為各節(jié)點的實際任務(wù)性能與理想任務(wù)性能間的差距。

Cares根據(jù)作戰(zhàn)過程中的不同角色將作戰(zhàn)環(huán)中的節(jié)點分為傳感器、決策者、影響者和目標(biāo)4種類型,并以此構(gòu)成閉合的作戰(zhàn)環(huán)。本文為了更好地描述由各部件組成的彈種在作戰(zhàn)過程中的整體關(guān)系,將元功能節(jié)點分為感知、測量、操控、動力、影響和目標(biāo)6種類型,如下所示:

Type=(S,M,C,P,I,T)

(7)

式中:S為元功能感知節(jié)點;M為元功能測量節(jié)點;C為元功能操控節(jié)點;P為元功能動力節(jié)點;I為元功能影響節(jié)點;T為元功能目標(biāo)節(jié)點。在本文的裝備體系結(jié)構(gòu)組成中,元功能感知節(jié)點代表截獲、跟蹤對方目標(biāo)的核心部件,包括:① 捷聯(lián)主動尋的導(dǎo)引頭;② 捷聯(lián)半主動尋的導(dǎo)引頭;③ 平臺主動導(dǎo)引頭;④ 平臺半主動導(dǎo)引頭。元功能測量節(jié)點代表測量導(dǎo)彈位置、姿態(tài)等信息的核心部件,包括:① 導(dǎo)航用IMU;② 控制用IMU。元功能操控節(jié)點代表根據(jù)導(dǎo)引信息操縱導(dǎo)彈運動的核心部件,包括:① 三通道舵機;② 雙通道舵機;③ 單通道舵機。元功能動力節(jié)點代表為導(dǎo)彈提供動力的核心部件,包括:① 超口徑高能量增程發(fā)動機;② 超口徑低特征信號增程發(fā)動機;③ 同口徑增速發(fā)動機。元功能影響節(jié)點代表執(zhí)行作戰(zhàn)過程中火力打擊任務(wù)的核心部件,包括:① 聚能破甲戰(zhàn)斗部;② 攻堅戰(zhàn)斗部;④ 爆破殺傷戰(zhàn)斗部。元功能目標(biāo)節(jié)點代表待打擊的對方目標(biāo)。

由此得到的元功能節(jié)點之間的關(guān)系和作戰(zhàn)環(huán)結(jié)構(gòu)如圖5所示。

圖5中,S1、S2、S3、S4分別為捷聯(lián)主動尋的導(dǎo)引頭、捷聯(lián)半主動尋的導(dǎo)引頭、平臺主動導(dǎo)引頭和平臺半主動導(dǎo)引頭;M1、M2分別為導(dǎo)航用IMU和控制用IMU;C1、C2、C3分別為三通道舵機、雙通道舵機和單通道舵機;P1、P2、P3分別為超口徑高能量增程發(fā)動機、超口徑低特征信號增程發(fā)動機和同口徑增速發(fā)動機;I1、I2、I3分別為聚能破甲戰(zhàn)斗部、攻堅戰(zhàn)斗部和爆破殺傷戰(zhàn)斗部。不同類型的部件之間可以組合成若干種子作戰(zhàn)環(huán)。

當(dāng)節(jié)點標(biāo)識為任務(wù)性時,用m表示;當(dāng)節(jié)點標(biāo)識為成本性時,用c表示。任務(wù)性節(jié)點的作戰(zhàn)環(huán)結(jié)構(gòu)如圖6所示。

成本性節(jié)點的作戰(zhàn)環(huán)結(jié)構(gòu)如圖7所示。

根據(jù)前文的定義,在各部件組成多種不同的彈種執(zhí)行相應(yīng)作戰(zhàn)任務(wù)的過程中會不可避免地存在一定程度的風(fēng)險,在這里將風(fēng)險定義為各節(jié)點的實際任務(wù)性能與理想任務(wù)性能之間的差距,如下所示:

Rm=(1-pm)vm

(8)

式中:Rm為各子作戰(zhàn)環(huán)中節(jié)點的風(fēng)險;pm為節(jié)點實際任務(wù)性能達到理想任務(wù)性能的概率,也即風(fēng)險系數(shù);vm為節(jié)點的理想任務(wù)性能。

在計算作戰(zhàn)環(huán)中各節(jié)點的整體作戰(zhàn)效能時采用如下公式:

En=Tpn·Δt-Rmn·Δt-Cpn·Δc

(9)

式中:En為作戰(zhàn)環(huán)中的各節(jié)點對裝備體系效能的絕對貢獻度;Tpn為該節(jié)點的任務(wù)性能絕對貢獻度;Δt為任務(wù)性能在裝備體系效能中的貢獻度;Rmn為該節(jié)點的風(fēng)險;Cpn為該節(jié)點的成本性能絕對貢獻度;Δc為成本性能在裝備體系效能中的貢獻度。

由此可得各子作戰(zhàn)環(huán)的整體作戰(zhàn)效能為

(10)

作戰(zhàn)過程中任一節(jié)點不能獨立發(fā)揮作用,各節(jié)點需相互協(xié)同共同組成彈種完成相應(yīng)的作戰(zhàn)任務(wù),不同類型的部件可以組合成若干種作戰(zhàn)環(huán),每一種作戰(zhàn)環(huán)代表一個彈種,優(yōu)化目標(biāo)為尋求滿足條件的最優(yōu)作戰(zhàn)環(huán)組合,也即彈種組合,使得裝備體系的效能最大,因此將該優(yōu)化問題的設(shè)計變量由指派模型中針對單一部件的0～1變量變?yōu)椴煌愋筒考湍繕?biāo)形成的作戰(zhàn)環(huán),可行解空間變?yōu)樽鲬?zhàn)環(huán)的數(shù)量,縮小了優(yōu)化問題的可行域,減少了計算時間。同時作戰(zhàn)環(huán)的引入也間接滿足了指派模型的約束條件,簡化了模型的求解過程。

4 算例分析

針對某導(dǎo)彈裝備體系,根據(jù)第1節(jié)建立的彈種優(yōu)化設(shè)計層次結(jié)構(gòu)模型,假定任務(wù)性能和經(jīng)濟性能對體系效能的貢獻度相同,均為0.5,且任務(wù)層中完成各項任務(wù)的能力對任務(wù)性能的貢獻度也相同,均為0.2。各層要素對上層的相對影響權(quán)重之和為1。結(jié)合導(dǎo)彈裝備體系的實際性能特點,采用專家打分法給出具體各層要素對上層的相對影響權(quán)重,也即相對貢獻度如表1～表16所示。

表1 子目標(biāo)層要素對上層的相對貢獻度

表2 任務(wù)能力層要素對上層的相對貢獻度

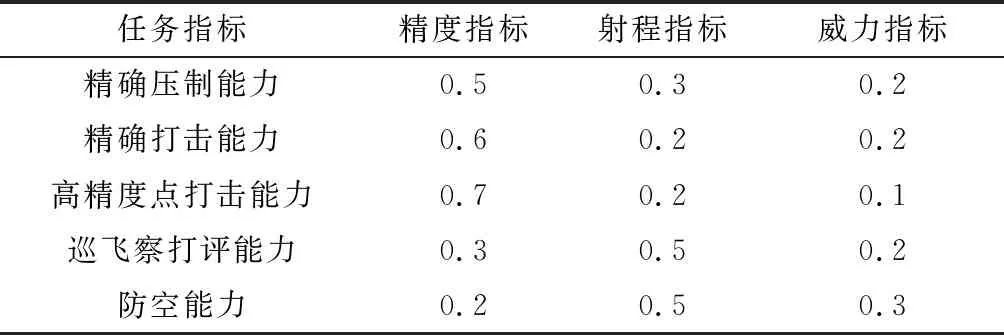
表3 任務(wù)指標(biāo)層要素對上層的相對貢獻度

表4 導(dǎo)引頭要素對指標(biāo)層的相對貢獻度

表5 IMU要素對指標(biāo)層的相對貢獻度

表6 舵機要素對指標(biāo)層的相對貢獻度

表7 發(fā)動機要素對指標(biāo)層的相對貢獻度

表8 戰(zhàn)斗部要素對指標(biāo)層的相對貢獻度

表9 成本層要素對上層的相對貢獻度

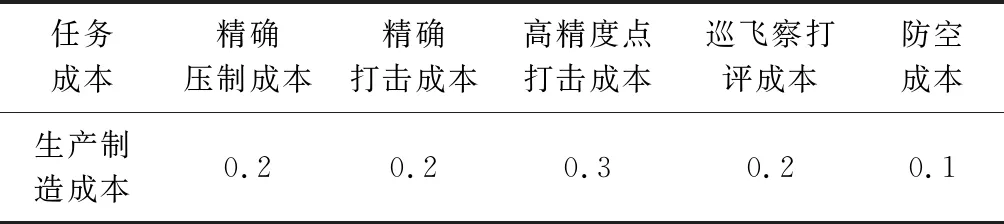
表10 任務(wù)成本層要素對上層的相對貢獻度

表11 成本指標(biāo)層要素對上層的相對貢獻度

表12 導(dǎo)引頭要素對導(dǎo)引頭成本層的相對貢獻度

表13 IMU要素對IMU成本層的相對貢獻度

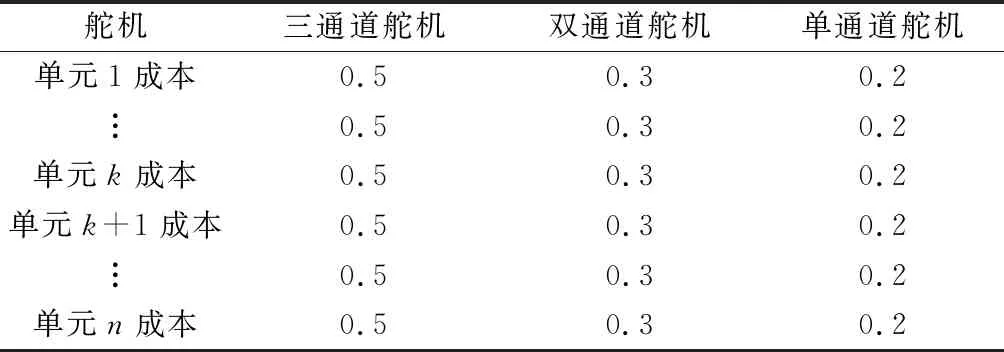
表14 舵機要素對舵機成本層的相對貢獻度

表15 發(fā)動機要素對發(fā)動機成本層的相對貢獻度

表16 戰(zhàn)斗部要素對戰(zhàn)斗部成本層的相對貢獻度

針對該導(dǎo)彈裝備體系,以一些離散的數(shù)值來表征不同類型部件的不同屬性,其中導(dǎo)引頭有效作用距離分別為8 km、9 km、10 km;IMU姿態(tài)精度為1°/h、2°/h、3°/h,位置精度為1 m/h、2 m/h、3 m/h;舵機的最大舵偏角為25°、30°、35°,最大舵偏角速度為200°/s、225°/s、250°/s;發(fā)動機的推力為40 kN、45 kN、50 kN,總沖為300 kN·s、350 kN·s、400 kN·s;戰(zhàn)斗部質(zhì)量為150 kg、175 kg、200 kg。為了表示不同的屬性參數(shù)值對部件任務(wù)性能和成本性能的影響,引入影響系數(shù),其取值范圍為[0,1],取值越大表示在該屬性參數(shù)下部件的任務(wù)性能和成本性能越高。不同類型的部件的各屬性參數(shù)值的影響系數(shù)如表17所示。

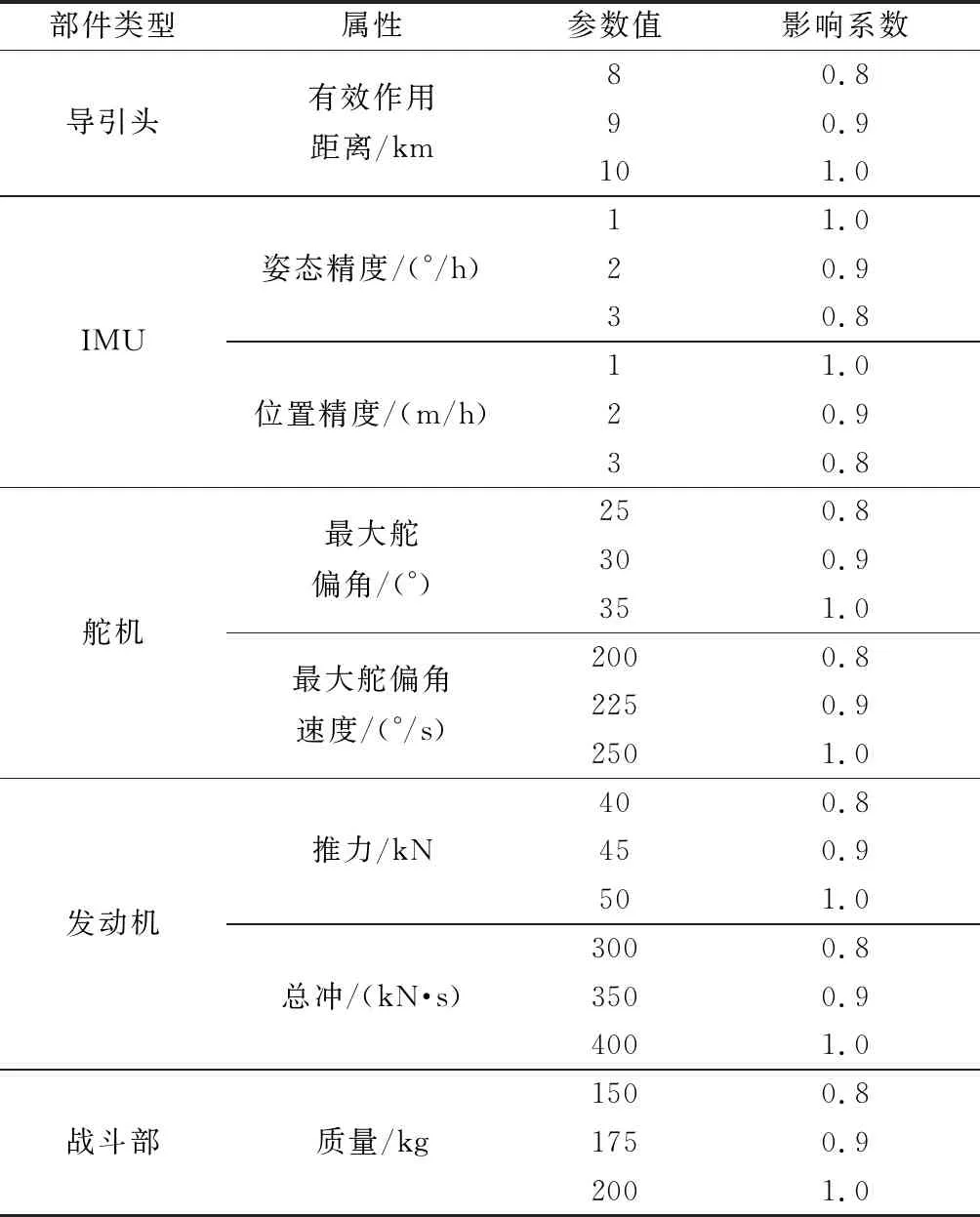
表17 不同部件屬性參數(shù)值的影響系數(shù)

根據(jù)作戰(zhàn)實際,將作戰(zhàn)環(huán)中節(jié)點S、M的風(fēng)險系數(shù)取為0.6,節(jié)點C、P、I的風(fēng)險系數(shù)取為0.7,則計算作戰(zhàn)環(huán)中各節(jié)點對裝備體系效能的絕對貢獻度的公式如下:

En=Tpn·γn·Δt-Rmn·Δt-Cpn·Δc

(11)

式中:En為作戰(zhàn)環(huán)中的各節(jié)點對裝備體系效能的絕對貢獻度;Tpn為該節(jié)點的任務(wù)性能絕對貢獻度;γn為該節(jié)點屬性參數(shù)值的影響系數(shù);Δt為任務(wù)性能在裝備體系效能中的貢獻度;Rmn為該節(jié)點的風(fēng)險;Cpn為該節(jié)點的成本性能絕對貢獻度;Δc為成本性能在裝備體系效能中的貢獻度。

根據(jù)式(11),可計算得出各子作戰(zhàn)環(huán)中不同屬性參數(shù)節(jié)點對裝備體系效能的絕對貢獻度。

根據(jù)第2節(jié)中給出的作戰(zhàn)環(huán)的定義,作戰(zhàn)過程中任一單獨的節(jié)點不能獨立完成作戰(zhàn)任務(wù),各節(jié)點需相互協(xié)同共同組成彈種完成相應(yīng)的作戰(zhàn)任務(wù)。由此可以計算得出不同屬性參數(shù)值的部件共有12×6×9×9×9=52 488種不同的組合,也即有52 488種不同的子作戰(zhàn)環(huán),每一種作戰(zhàn)環(huán)代表一個彈種,因此該優(yōu)化問題的可行域為52 488種作戰(zhàn)環(huán)。用于判斷作戰(zhàn)環(huán)是否入選最優(yōu)組合的條件是作戰(zhàn)環(huán)的整體任務(wù)性能、成本性能和風(fēng)險之間的關(guān)系,若某子作戰(zhàn)環(huán)的任務(wù)性能大于成本性能和風(fēng)險的和,即對裝備體系的綜合作戰(zhàn)效能產(chǎn)生積極影響時,則該作戰(zhàn)環(huán),也即該彈種入選最優(yōu)組合;若某子作戰(zhàn)環(huán)的任務(wù)性能小于成本性能和風(fēng)險的和,即對裝備體系的綜合作戰(zhàn)效能產(chǎn)生消極影響時,則該彈種不能入選最優(yōu)組合,即滿足：

(12)

式中:i的最大值為12+6+9+9+9=45,即有45種不同屬性參數(shù)值的備選部件。

由此可以得出該優(yōu)化問題在指派模型的基礎(chǔ)上采用快速求解方法簡化的數(shù)學(xué)模型如下所示:

Rmni·Δt-Cpni·Δc)k

i=1,2,…,45;k=1,2,…,52 488

(13)

對上述模型進行求解,可以得出最優(yōu)的作戰(zhàn)環(huán)組合及相應(yīng)的參數(shù)值和對體系效能的絕對貢獻度如表18所示。同時分別采用經(jīng)典的割平面法和分支定界法對第2節(jié)中建立的優(yōu)化問題指派模型進行求解得到的結(jié)果分別如表19和表20所示。表21給出了分別采用3種方法的計算求解時間。

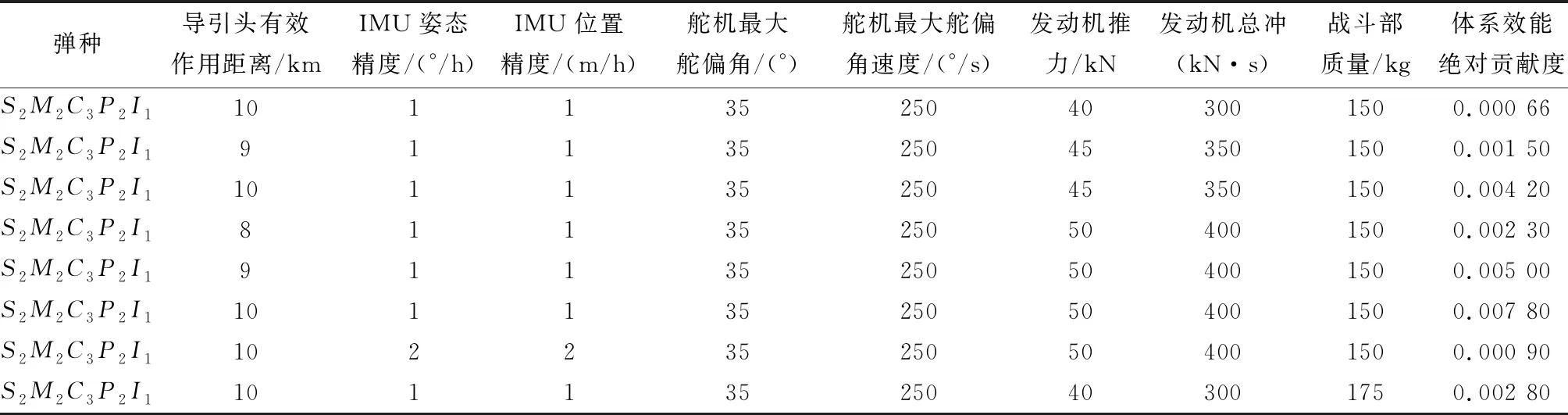
表18 采用基于作戰(zhàn)環(huán)的快速求解方法得到的最優(yōu)彈種組合及參數(shù)值和相應(yīng)體系效能絕對貢獻度

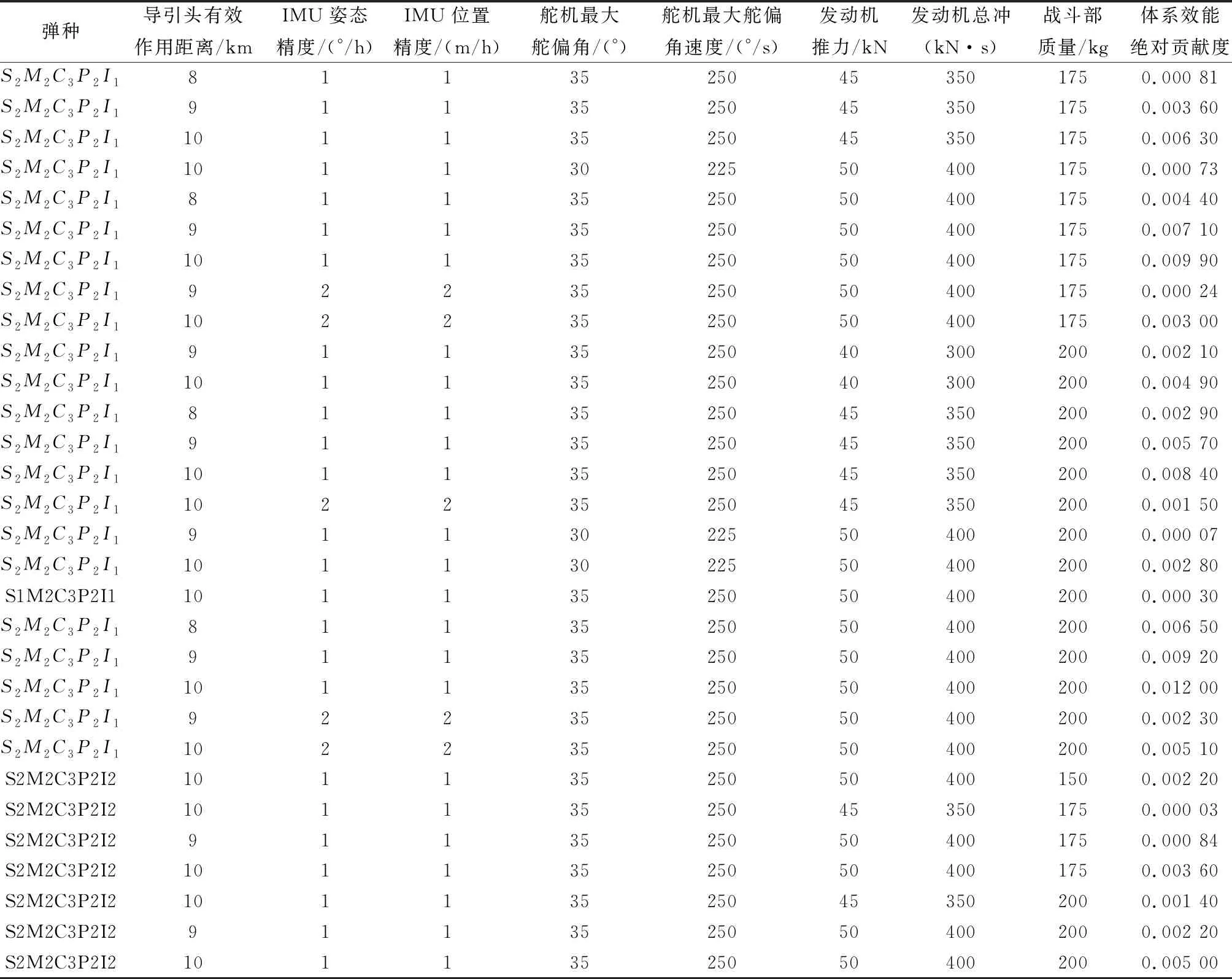
續(xù)表18

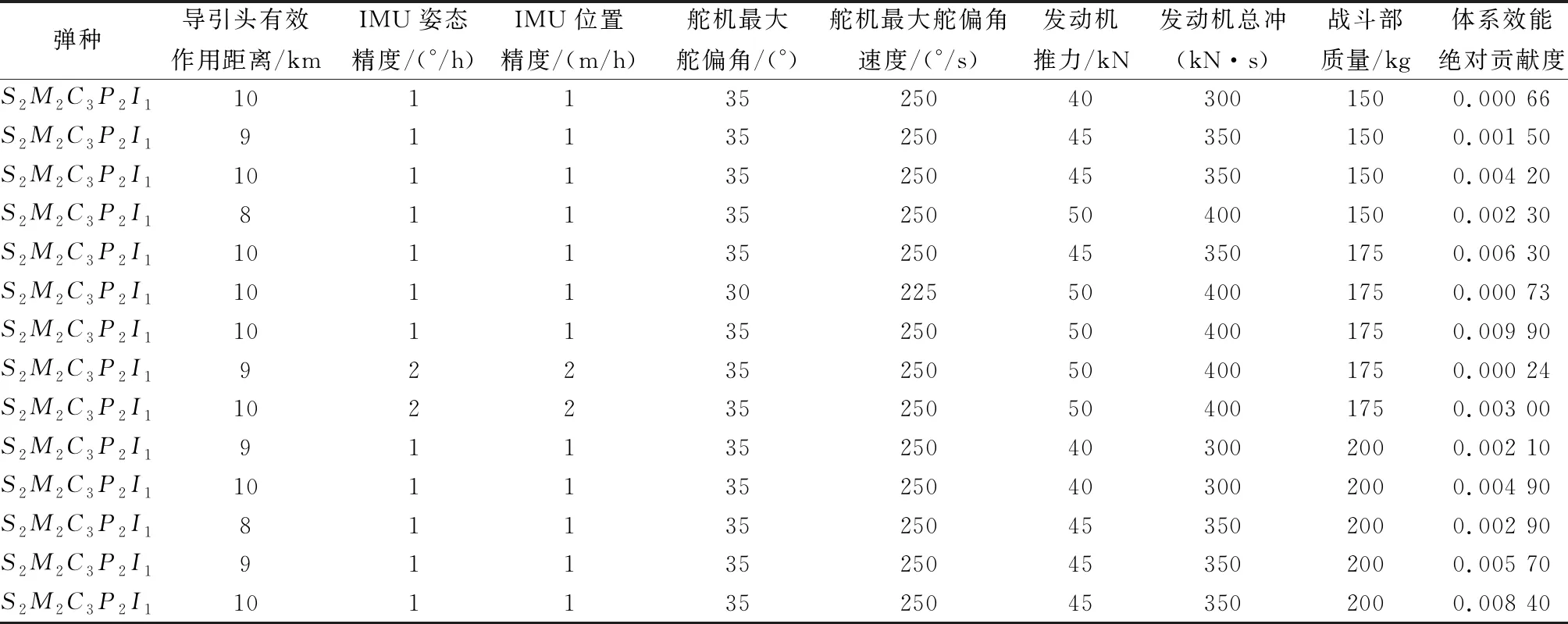
表19 采用割平面法得到的最優(yōu)彈種組合及參數(shù)值和相應(yīng)體系效能絕對貢獻度

續(xù)表19

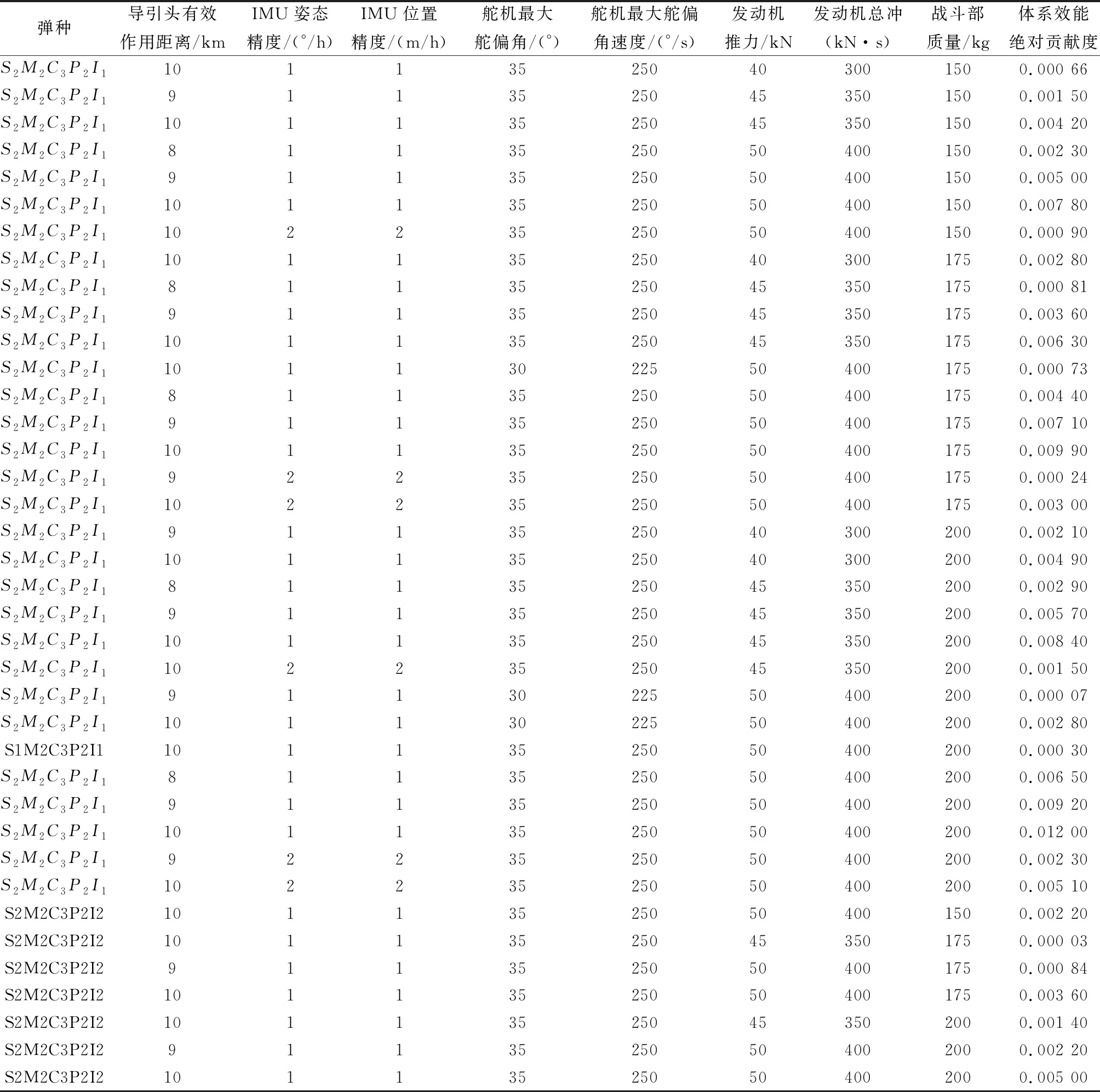
表20 采用分支定界法得到的最優(yōu)彈種組合及參數(shù)值和相應(yīng)體系效能絕對貢獻度

表21 采用3種方法所用計算求解時間

從表18的結(jié)果中不難看出,最優(yōu)的彈種組合中部件均采用了IMU部件中的控制用IMU、舵機部件中的單通道舵機、發(fā)動機部件中的超口徑低特征信號增程發(fā)動機,導(dǎo)引頭分別采用了捷聯(lián)主動尋的導(dǎo)引頭和捷聯(lián)半主動尋的導(dǎo)引頭;戰(zhàn)斗部分別采用了聚能破甲戰(zhàn)斗部和攻堅戰(zhàn)斗部,各彈種對應(yīng)的表征部件屬性的參數(shù)值不同。針對導(dǎo)彈種類層中不同類型的導(dǎo)彈,表18得出的不同參數(shù)的部件組合決定了最終彈種層中的彈種組合。由于彈種組合中導(dǎo)引頭采用了捷聯(lián)主動尋的導(dǎo)引頭和捷聯(lián)半主動尋的導(dǎo)引頭,IMU采用了控制用IMU,故最優(yōu)的彈種組合中不包括激光駕束制導(dǎo)導(dǎo)彈、慣性制導(dǎo)導(dǎo)彈和無控導(dǎo)彈。綜合表18中最優(yōu)彈種組合的參數(shù)值,可以得出彈種層的最優(yōu)彈種組合為衛(wèi)星制導(dǎo)導(dǎo)彈、激光半主動制導(dǎo)導(dǎo)彈、巡飛導(dǎo)彈和防空導(dǎo)彈,從而使得裝備體系的綜合效能最大。

而從表19～表21的結(jié)果中可以看出,采用割平面法求解存在多組最優(yōu)解的整數(shù)線性規(guī)劃問題時會造成遺忘解的存在,無法得出全部最優(yōu)解,且計算耗時較長;采用分支定界法求解該優(yōu)化問題時雖然也能得出和基于作戰(zhàn)環(huán)的快速求解方法相同的全部最優(yōu)解,但相比基于作戰(zhàn)環(huán)的快速求解方法計算求解時間成倍增長,且分支定界法的效率基本上由值界方法決定,若界估計不好,在極端情況下將與窮舉搜索法區(qū)別不大,難以滿足快速準(zhǔn)確求解的要求。

本節(jié)通過引入具體算例進行優(yōu)化求解,驗證了第2節(jié)建立的指派模型的有效性,同時在對模型進行求解的過程中如果采用經(jīng)典的指派模型求解方法將直接在212+6+9+9+9=245個決策變量構(gòu)成的可行域內(nèi)搜索滿足約束條件的解,以每個決策耗時約9.4×10-5s計算,計算耗時將達到3.3×109s。采用割平面法和分支定界法雖然在很大程度上縮小了計算求解時間,但在計算求解精度和效率方面仍存在較大的劣勢。而引入作戰(zhàn)環(huán)不僅考慮了不同類型部件協(xié)同工作的影響關(guān)系,強化了優(yōu)化問題的約束條件,而且極大縮小了該優(yōu)化問題的可行域(決策變量為52 488個),在求得全部最優(yōu)解的情況下計算耗時僅為4.93 s,因此可以實現(xiàn)對該模型的快速準(zhǔn)確求解。

5 結(jié) 論

本文以通用設(shè)計模塊為基礎(chǔ)進行多彈種的體系優(yōu)化設(shè)計,并按照AHP的思想對通用設(shè)計模塊進行層次劃分,建立了導(dǎo)彈裝備體系效能引導(dǎo)的彈種優(yōu)化設(shè)計結(jié)構(gòu)框架,以綜合考慮任務(wù)、成本和風(fēng)險影響因素的裝備體系效能最優(yōu)為目標(biāo),構(gòu)建了指派模型。針對經(jīng)典求解方法在應(yīng)對可行解空間較大的優(yōu)化問題時所表現(xiàn)出的局限性,設(shè)計基于作戰(zhàn)環(huán)的快速求解方法,將不同類型的導(dǎo)彈部件組合為整體的彈種對模型進行快速優(yōu)化求解。通過引入具體算例對所建立的模型和快速求解方法進行了驗證,并將得到的結(jié)果與采用經(jīng)典求解方法得到的結(jié)果進行對比分析,所得主要結(jié)論如下。

(1) 引入通用設(shè)計模塊進行導(dǎo)彈裝備體系彈種優(yōu)化設(shè)計有利于提高設(shè)計效率、降低設(shè)計成本,同時根據(jù)AHP的思想建立的彈種優(yōu)化設(shè)計層次結(jié)構(gòu)模型能夠以貢獻度的形式比較清晰完整地反映導(dǎo)彈裝備體系中各層要素之間的關(guān)系,為部件層級以及彈種層級的進一步優(yōu)化設(shè)計提供背景框架。

(2) 本文所建立的基于指派問題的彈種優(yōu)化設(shè)計模型能夠?qū)崿F(xiàn)導(dǎo)彈裝備體系中最優(yōu)彈種設(shè)計方案的求解。

(3) 基于作戰(zhàn)環(huán)的快速優(yōu)化求解方法將不同類型的導(dǎo)彈部件組合為整體的彈種對模型進行求解,可以增強該優(yōu)化問題的約束條件,從而大幅縮小可行域,實現(xiàn)對模型的快速準(zhǔn)確求解,加快導(dǎo)彈裝備體系彈種優(yōu)化設(shè)計過程。