樞軸量選取對正態總體方差區間估計的影響

王晶，劉彭

（山東農業大學 信息科學與工程學院，山東 泰安 271018）

參數估計方法是基礎的統計推斷方法之一，此類方法在自然科學和社會科學各領域涉及到數據分析的問題中被大量使用.在實際問題中，人們感興趣的問題往往與分布族中的未知參數有關.參數估計方法是在總體分布形式已知時，利用樣本值對分布中某一個或某幾個未知參數值進行統計推斷的方法，一般分為點估計和區間估計問題.

在總體分布形式已知時，對于其分布中的未知參數θ，除了求出其點估計外，還希望估計出一個范圍，使其以較大可信度包含參數θ的真值.這樣的范圍通常以區間形式給出，同時還給出其包含參數θ真值的可信程度，這種形式的估計稱為參數的區間估計，而這樣的區間稱為參數θ的置信區間[1].

定義1[2]設總體X的分布中含有未知參數θ,若有來自總體X的一組樣本（X1,X2,…,Xn）確定的2個統計量，使得對于給定的α（0＜α＜1），有，則稱隨機區間是參數θ置信度為1-α的置信區間，分別稱為置信下限和置信上限，1-α稱為置信度.

在經典統計學中，構造參數θ的置信區間最常用的方法是樞軸量法，其基本步驟可概括為：

Step1選取樣本（X1,X2,…,Xn）的一個函數G（X1,X2,…,Xn;θ），其中只含所求置信區間的未知參數θ，且分布已知；

Step2對于給出的置信水平1-α，確定Step1 中分布的雙側分位點λ1，λ2，則有

Step3利用不等式變形得到未知參數θ的置信區間.

構造置信區間的方法關鍵在于Step1 中所選取的函數G（X1,X2,…,Xn;θ）為樞軸量.關于樞軸量，在大部分概率統計教材中對其是這樣描述的：選取合適的統計量，要求包括待檢驗的參數，不含其它任何未知參數，且統計量的分布已知[3]，滿足這種要求的統計量即為在區間估計中所謂的樞軸量[4-5].而在參數的區間估計問題中，即使是對同一個未知參數求置信區間，滿足以上條件的統計量也往往不是唯一的，此時就面臨著如何選取樞軸量的問題.針對選擇不同的樞軸量得到的置信區間其性質是否有差別，不同樞軸量下得到的同一參數的置信區間之間是否有優劣之分問題，本文以單個正態分布總體中方差σ2這一參數的區間估計問題為例進行討論.

1 基于2 種不同樞軸量的正態總體方差區間估計

設總體X～N（μ,σ2），其中總體均值μ已知，（X1,X2,…,Xn）為來自總體容量為n的簡單隨機樣本，則有

式中：X為樣本均值.

2 2 種置信區間比較

2 種區間（3）（4）是基于不同樞軸量對單個正態總體方差σ2進行區間估計的結果，若要對其優劣進行比較主要基于可靠度和精度2個指標.在區間估計中，置信度1-α反映的是估計的可靠性程度，置信度越大，估計的可靠性程度也就越大；置信區間的長度反映的是估計的精度，置信區間長度越短，估計的精度也就越高.在樣本容量n一定的情況下，這2個要求往往是互相矛盾的[6].在實際應用中，置信度一般按照應用需求直接給定，可靠性已經確定，此時可認為平均長度較小的置信區間精度較高，估計結果更好.

對于置信區間（3），其平均長度為

對于置信區間（4），其平均長度為

因此可構造兩者比值，其為樣本容量n的函數，記為

顯然n=1 時，，此時L1=L2.當n＞ 1時，g(n)的部分結果見表1（α=0.05）.由表1可見，隨著n的增大，置信區間對應g(n) 的差值逐漸減小，即隨著樣本容量增大，2種置信區間平均長度比逐漸趨于穩定.

表1 不同樣本容量下2 種置信區間的平均長度比

在SPSS22.0[7-8]中得到樣本容量n∈［1,20］及n∈［1,100］時函數g(n)變化趨勢（見圖1）.

圖1 置信區間長度比變化趨勢

由表1 和圖1可以看出，當n＞ 1時，g(n)的值隨著n的增大持續變小，n＞ 5時變化趨于平緩，因此對任意樣本容量n，總有g(n) ≤ 1，即L1≤L2，在相同的置信度下，置信區間（3）的精度優于置信區間（4）.在總體均值已知情形下，用樞軸量（3）對單個正態總體的方差σ2進行區間估計效果更好.

為了進一步對結論進行驗證，可從特定正態總體中抽樣隨機模擬獲得直觀比較結果.設總體X～N(0,1），即參數σ2的真值為1.運用R 軟件[9]，從此分布總體中隨機抽取100 組容量為n的樣本，根據式（3）～（4），由隨機抽樣結果分別計算σ2置信度為95%的100 個置信區間.n=10，n=100時100個置信區間的模擬結果分別見圖2～3.

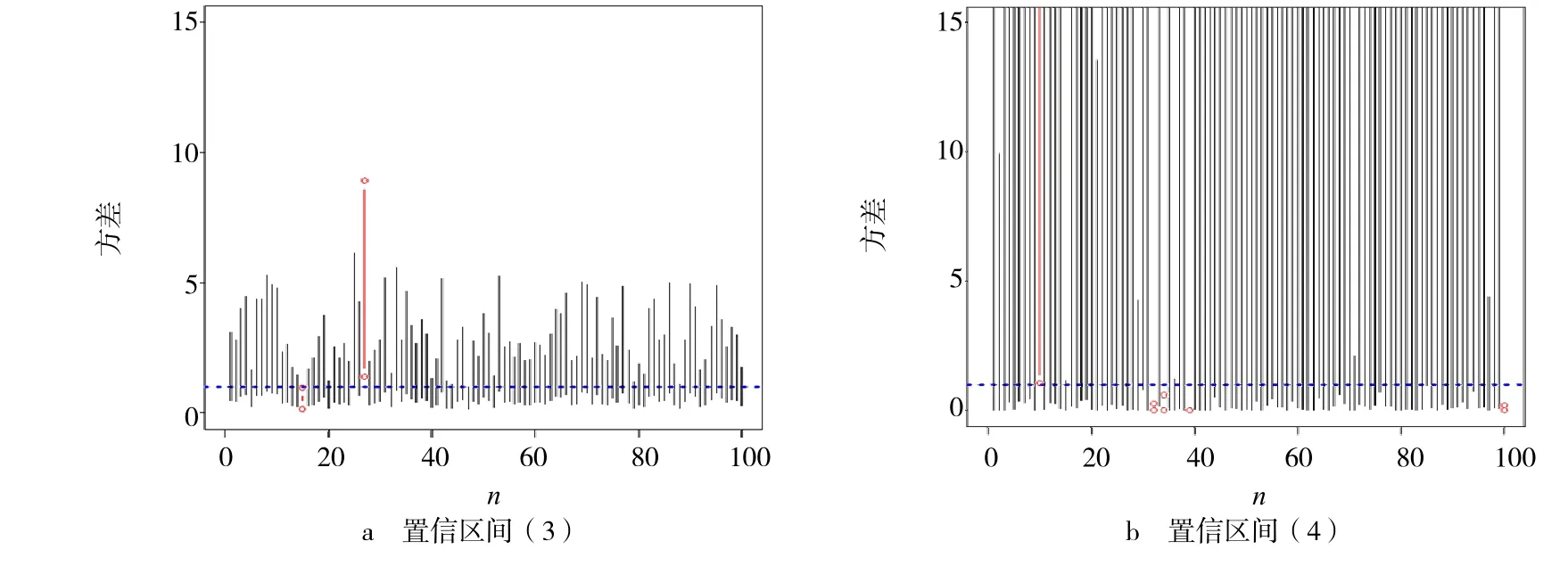
圖2 樣本容量為10 時的100 個置信區間

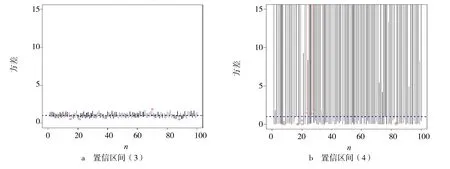
圖3 樣本容量為100 時的100 個置信區間

由圖2～3 可以看出，2種情形下均有置信區間（3）的平均長度遠小于置信區間（4）的平均長度.相比較下，用樞軸量對單個正態總體的方差σ2進行區間估計，置信區間精度較高，結果更好.

3 實例驗證

利用2種方法在總體均值已知情況下，對正態總體方差σ2進行區間估計，通過具體實驗結果的計算比較，也能看到置信區間（3）的精度較高.

例[10]發芽期隨機抽取某種作物16 株，對株高進行測量，測得株高（單位：cm）數據分別為2.15，2.10，2.12，2.10，2.14，2.11，2.15，2.13，2.13，2.11，2.14，2.13，2.12，2.13，2.10，2.14.求株高標準差σ的95%置信區間（設總體X～N（2,σ2））.

解由實際測量數據，根據式（3）～（4）分別可計算得到株高方差σ2和標準差σ的95%置信區間，結果見表2.

表2 2種不同方法下株高方差和標準差的置信區間

對于該例題，在2種區間估計方法下，具體算得的置信區間差別比較大，顯然此例中置信區間（3）的長度遠遠小于置信區間（4），說明其精度較高.在實際應用中，在可靠度一定的情況下，精度高的置信區間是應該優先選擇的，而在經典教科書中對于此類均值已知情形下正態總體方差的區間估計均選用樞軸量進行構造，是有其深刻意義的.可見，樞軸量的選擇是有其標準可言的.

4 結語

通過總體均值已知時單個正態分布總體方差σ2參數的區間估計問題，初步闡述了樞軸量的選取標準及其對置信區間結果的影響.在進行置信區間的評價時，可靠性和精度是2個基本標準，而它們也與樣本容量n的大小有直接關系，在此不再深入探討.需要注意的是當考慮置信區間精度這一標準時，應盡量選擇區間平均長度小的置信區間.在討論2種情況下置信區間的平均長度大小關系時，對不同樣本容量n的進行了直觀模擬.由于比值函數中包含χ2分布分位點，其值為χ2分布的分布函數的反函數值，其取值范圍的嚴格證明仍需要進行更深層次的思考.