讓學生學習『講道理』的數學

文 高飛

道理，《現代漢語詞典》解釋說：①事物的規律；②事情或論點的是非得失的根據；理由；情理；③辦法；打算。讓學生學習“講道理”的數學，一方面是指引導學生發現數學知識的本質規律;另一方面是指促動學生闡明數學知識產生、發展和形成的依據或理由，等等。讓學生學習“講道理”的數學，不僅有助于學生“觸摸”數學知識的本質，提升數學知識的理解水平，而且有助于學生明確數學知識規定的合理性，理解基本技能操作的程序與步驟的道理，培養學生地數學思維能力。綜上所述，在數學學習中，引導學生發現與詮釋數學知識產生、發展、形成和應用的道理，是實現數學深度學習目標的重要措施之一。那么，在數學教學中，如何引導學生學習“講道理”的數學，達成深度學習的目標呢？

一、立足本質“講道理”，促進學生理解概念的內涵

概念教學是小學階段重點教學內容之一。概念教學的要求是使學生經歷概念的產生、發展和形成的過程，促進學生理解概念的本質內涵，達成“知其然，又知其所以然”的目標。為此，在概念教學中，教師要從概念的本質屬性出發，設計適當的教與學的活動，引導學生經歷對概念例證的觀察、操作、推理、抽象、概括和交流等認知活動，通過講好概念形成的道理，促進學生體驗概念的本質屬性，達成對概念內涵的深刻理解。

點到直線的距離（蘇教版數學四年級上冊）是圖形與幾何領域的重要概念之一。它是學生認識各類圖形的高的認知基礎。眾所周知，數學上，之所以確定從已知點到已知直線的垂直線段作為點到直線的距離，其根本原因是它的唯一屬性，而非長度最短的特征。為此，教材先是從已知點向已知直線引出若干條線段，然后，通過測量活動，引導學生探索并發現在這些線段中，與已知直線相互垂直的線段的長度“最”短。力求從詞意上，通過“最”字的體悟，幫助學生感受與已知直線相互垂直線段的唯一性。為此，在實際教學中，通常采取的教學路徑是：出示從已知點到已知直線的若干條線段—引導學生猜測哪條線段最短—通過測量進行驗證，得出結論—揭示點到直線距離的概念。不難看出，不管是猜測環節，還是驗證環節，學生的注意力及其探究聚焦點無不集中在“線段的長度”上，從而“短”字成為了探究學習過程中的“強刺激”，而體現與已知直線相互垂直線段的唯一性的“最”字的感悟，無形中被“弱化了”。最終，通過系列活動，學生只是強烈感受了“垂直線段最短”。無疑，學生的體會和教材的編排意圖“相距甚遠”。那么，如何幫助學生體會點到已知直線的垂直線段的唯一性，進而幫助學生理解點到直線的距離的內涵呢？

出示圖1：

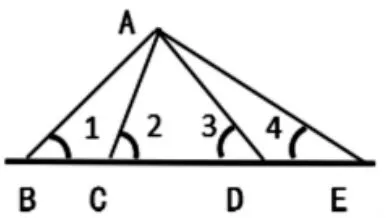
圖1

如圖1，在已知直線上任取點B，連接點AB，線段AB 和已知直線的夾角為∠1，接著，繼續畫出線段AC、AD 和AE，夾角分別是∠2、∠3 和∠4。

互動1：像AB、AC、AD 和AE這樣，從A 點到已知直線的線段，能畫多少條？為什么？

引導學生從“直線上有無數個點”，或者重點從“像AB、AC、AD 和AE 這樣的線段與已知直線的夾角，如∠1、∠2、∠3 和∠4 都是銳角，因為銳角有無數種，所以，這樣的線段能畫無數條”的角度，理解及闡述像AB、AC、AD 和AE 這樣的線段有無數條的道理。

互動2：從A 點到已知直線的線段中，“有且只有一條”的線段在哪里？它與已知直線有什么關系？找一找、畫一畫，說明理由。

引導學生借助圖形，找出與已知直線互相垂直的線段（如圖2，AF），并從“AF 與已知直線的夾角是直角，直角是唯一的”的角度，說明線段AF 的唯一性。

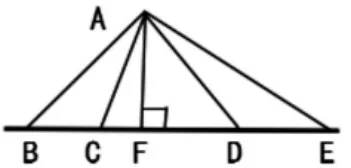
圖2

互動3：量一量AB、AC、AD、AE 和AF，你有什么發現？

通過測量，使學生認識“從直線外一點到已知直線的垂直線段是最短的”的特征。

最后，揭示點到直線的距離概念。

角是學生熟悉的知識。特別是，經歷小數的初步認識、角的測量和分類等知識技能學習以后，學生對“銳角有無數個”“直角是唯一的”的認識更加充分而深入。為此，案例中，教師“另辟蹊徑”從學生已有的“角”的經驗出發，引導他們借助“銳角有無數個”“直角是唯一的”的認知與體驗，通過推理和想象等活動，感受從直線外一點到已知直線的線段中，與已知直線互相垂直的線段“只有一條”的特性，從而助力學生體會點到已知直線的垂直線段的唯一性，促進學生理解點到直線的距離的內涵，更重要的是，自始至終引發了學生思維活動的深度參與，達成了深度學習的目標。

二、立足意義“講道理”，促進學生理解計算的道理

運算能力主要是指能夠根據法則和運算律正確地進行計算的能力，培養運算能力有助于學生理解運算的算理，尋求合理簡潔的運算途徑解決問題。因此，計算教學在促使學生熟練掌握算法的同時，還要促進學生理解計算的道理。然而，教學假分數化成帶分數（蘇教版數學五年級下冊）時，教師通常是不講“道理”的。學生往往僅憑教師的簡單傳授“分子除以分母的‘商’作帶分數的整數部分，‘余數’作分子，‘分母’不變”進行模仿和操練。試想：“假分數化成帶分數用分子除以分母，為什么‘商’‘余數’分別是帶分數的整數部分和分子，分母不變呢？”對這些問題的思辨、解釋和澄清，正是學生學習假分數化成帶分數必須經歷的、不可省卻的思考過程！否則，就嬗變為“知其然，而不知其所以然”的機械學習。為此，教學中，教師可以借助幾何直觀手段，引導學生自主構圖并利用圖形詮釋假分數化成帶分數的“算理”：

互動1：分子不是分母的倍數的假分數，怎樣化成帶分數？試一試。

生1：

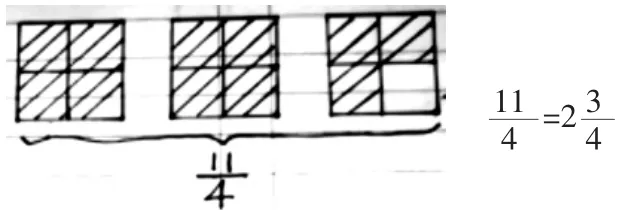
圖3

互動2：（指生2）能不能借助生1 的圖形，說說你是怎樣想的？

接著，讓學生“趁熱打鐵”繼續將幾個假分數化成帶分數，并發現把假分數化成帶分數“用分子除以分母的商作帶分數的整數部分，余數作分子，分母不變”的規律。

假分數化成整數和帶分數的“算理”理解，需要學生從“包含除”的視角進行探索與思考。案例中，把化成帶分數。有的學生通過構造圖形描述，從而“看”出；有的學生聯系分數與除法的關系，通過11÷4=2……3，推導出。為此，教師巧妙利用生成“資源”追問生2：“能不能借助生1 的圖形，說說你是怎樣想的？”板演學生“心有靈犀”，借著圖形，有根有據地闡明了的數學道理，同時，欣然理解：“為什么要每4 個分成一份呢？而不是2 個、3 個？”從而突破了假分數化成帶分數的“算理理解”的難點，達成了深度學習的目標。

三、立足需要“講道理”，促進學生理解操作方法的合理性

《數學課程標準（2011年版）》指出：“在基本技能教學中，不僅要使學生掌握基本技能操作的程序和步驟，還要使學生理解程序和步驟的道理。”畫平行線是小學數學學習的重要技能之一，教材（人教版數學四年級上冊）基本上是采取“直接告知”的方式進行教學的。即以“圖示”的方式，在分步演示選擇什么工具，怎樣操作的基礎上，引導學生討論、歸納操作步驟和方法。但是，畫平行線的基本原理是什么？作圖時，可能遇到什么困難？為什么用兩把尺子“合作”等等，對這些問題的體驗、質疑和闡釋，正是學生理解畫平行線的方法和步驟需要經歷的、不可逾越的思考過程。那么，在教學中，如何引導學生體會平移和平行的關系，經歷畫平行線的工具選擇、方法優化、畫法概括等思維過程，促進學生理解操作的合理性？

動畫出示：

圖4

互動1：說說推拉窗和五星紅旗分別是什么運動？用鉛筆在方格紙上移一移、畫一畫，你發現了什么？

引導學生用鉛筆在方格紙上，模仿推拉窗和五星紅旗的運動軌跡，移一移、畫一畫，使學生體驗平移和平行的關系，促進學生認識通過平移可以得到兩條互相平行的直線。

互動2：你能在紙上，利用平移畫出兩條互相平行的直線嗎？試一試，你有什么感受？

通過操作，促使學生體驗利用直尺或三角尺進行平移時，會出現“偏軌”現象，產生解決問題的心理需求。

互動3：想一想，有什么改進的辦法嗎？議一議。

激發學生積極調用已有經驗，優化工具，改進操作方法：在三角尺的另一條直角邊上，貼緊一把直尺或三角尺作“軌道”，平移時不會發生“偏軌”的現象，體驗選用兩把尺子的必要性，理解畫平行線的方法。

互動4：你能畫出一組互相平行的直線嗎？說一說畫平行線時，要注意什么？

利用改進后的操作工具及其方法，畫一組互相平行的直線，并總結畫平行線的方法（略），促進學生體驗選擇工具的必要性及其操作方法的合理性。

案例中，通過動畫演示兩組平移的現象，同時，引導用鉛筆在方格紙上模仿兩組平移現象畫出兩組平行線，促使學生體會平移與平行的內在聯系，認識通過平移方式可以畫出一組互相平行的直線。在此基礎上，引導學生自主選擇工具，通過在紙上畫平行線，促進他們體驗用一把尺子進行平移畫平行線的局限性，產生認知沖突，形成“迫切”解決問題的心理需求，從而促動學生積極討論改進畫平行線的操作工具及其方法。整個教學過程，學生經歷了平行線的畫法及工具的選擇、優化與調整的反思、嘗試等思維過程，深刻體會了畫平行線工具選擇的必要性及其操作方法的合理性，達成了“知其然，又知其所以然”的目標，積累了尺規作圖的活動經驗，提升了操作能力。