隔震結構復振型分解反應譜方法研究

楊 奎， 譚 平， 陳華霆， 李曉磊

(1. 廣州大學 廣東省地震工程與應用技術重點實驗室，廣州 510405；2. 廣州大學 工程抗震減震與結構安全教育部重點實驗室，廣州 510405)

隔震結構一般由上部結構和隔震系統組成，由于兩者阻尼特性不同，形成了典型的非比例阻尼體系。非比例阻尼特性對隔震結構的動力響應是不可忽略的[1-2]。對于隔震結構設計，按照我國GB 50011—2010《建筑結構抗震設計規范》可采用基于水平向減震系數的分部設計方法，其地震作用計算采用強迫解耦的傳統反應譜方法[3]，但沒有充分考慮非經典阻尼的影響。由于強迫解耦法缺乏理論依據，所以很多科研人員致力于復模態的研究[4-6]。

Chen等[7]提出了有效的非經典阻尼體系荷載Ritz向量生成算法，進一步提高了計算效率。為了降低計算規模，僅考慮低階振型參與計算，同時考慮高階振型影響，陳華霆等[8]提出了復振型加速度方法。上述研究成果為復振型疊加方法向工程應用奠定了基礎。Igusa等[9-10]在復模態理論的框架下，假定地震動為平穩白噪聲過程，給出了各自的組合規則，但其振型相關系數較為復雜。周錫元等[11]利用復平面圍道積分理論推導出了解析形式的振型位移-位移、速度-位移和速度-速度的相關系數，提出了簡便的復振型完全平方組合(complex complete quadratic combination，CCQC)組合規則。之后，Yu等[12-13]又將CCQC方法推廣到了多維、多點地震輸入的情況，Liu等[14]進一步在多點地震輸入的反應譜方法中考慮了等效地震荷載中阻尼的影響，Chen等[15]基于模態擴展方法在CCQC中引入了截斷的高階振型貢獻。由于復模態分析中，所要求解特征值問題的規模是系統自由度的兩倍，限制了復振型疊加方法的應用。因此當前相關科研人員主要從事對其進行優化和擴展應用上，本文將在上述研究的基礎上重點討論阻尼矩陣構造對隔震結構復振型分解反應譜法的影響。

非比例阻尼矩陣的構造是復振型分解反應譜法實施的基礎，對其開展相關研究是非常必要的。本文以隔震結構為研究對象，分別以瑞利阻尼、振型疊加阻尼系數和阻尼比換算阻尼系數3種方法，根據隔震結構特點，按照剛度矩陣的集裝方式來組裝形成4種不同的整體非比例阻尼矩陣。采用兩種不同的天然波反應譜，以反應譜CCQC和反應譜完全平方組合(complete quadratic combination，CQC)分析不同阻尼矩陣形成方式對結構響應的影響以及隔震層等效周期、等效阻尼比、地震動特性對CQC和CCQC方法計算精度的影響，最后基于分析結果以設計反應譜CQC和設計反應譜CCQC研究隔震層不同等效周期和等效阻尼比對隔震結構的樓層位移和樓層剪力誤差影響。

1 隔震結構運動方程

基礎隔震結構計算簡圖可簡化，如圖1所示。圖1中：mb,kb為隔震層的質量和等效剛度；m1～mn為上部結構各層質量；k1～kn為上部結構各層的剛度；x1～xn為各層相對地面的位移。

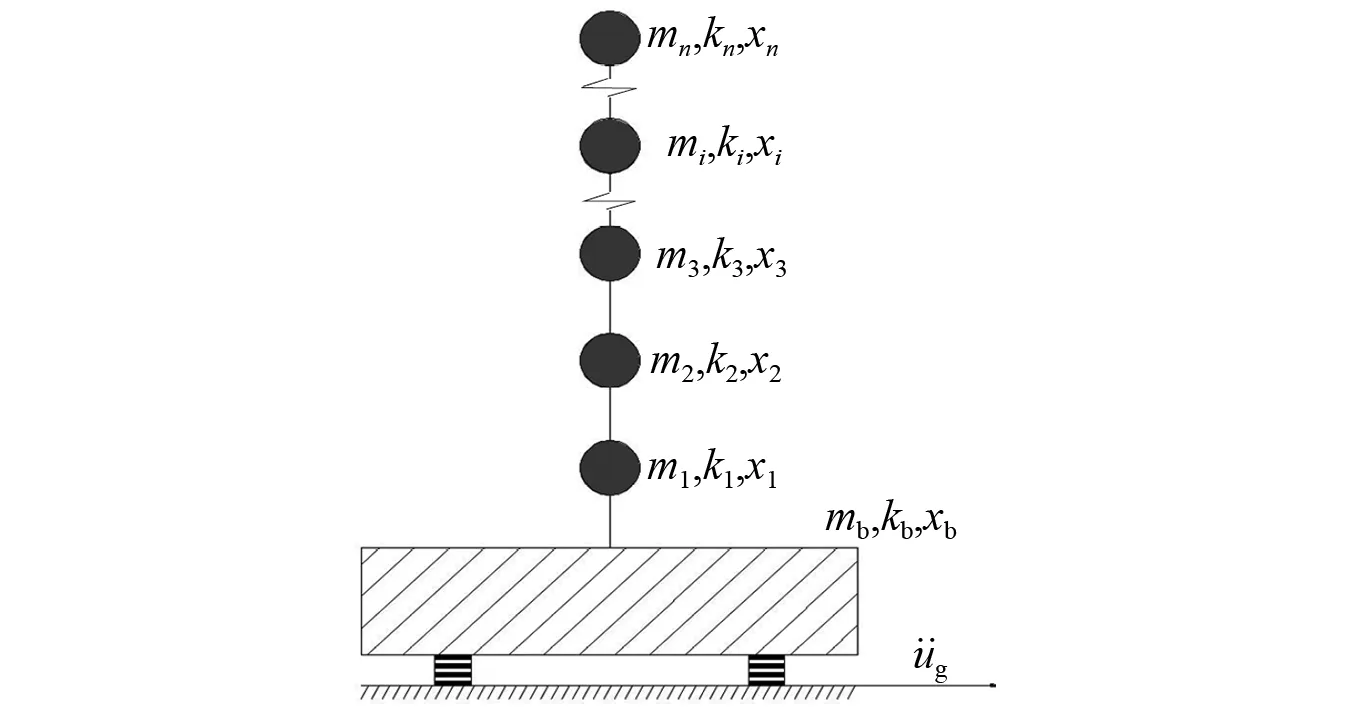
圖1 隔震體系模型示意圖

針對圖1隔震結構運動示意圖，以各質點相對地面作為運動變量。該體系在地震作用下的運動方程可表達為

(1)

由于隔震層與上結構材料不同，兩者的阻尼有明顯差異，所以在其運動方程在振型空間展開具有耦合項，如式(2)所示。

式(1)中x在無阻尼空間Φ展開，即x=Φq，則式(1)可由振型運動方程表示

(2)

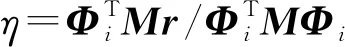
2 隔震結構反應譜CCQC法理論

為對式(1)中隔震結構運動方程進行解耦，需要利用Foss變換[16]將其轉化為2n個一階微分方程，即

(3)

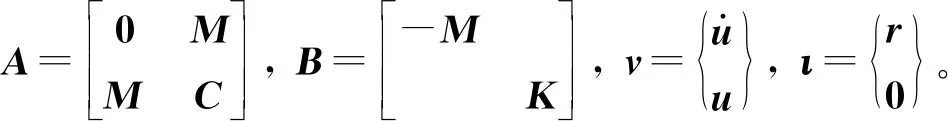
矩陣A和B為對稱非正定矩陣，利用式(4)可求得結構的特征值和特征向量

(λA+B)ψ=0

(4)

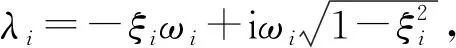
(5)

式中， Re(·)和Im(·)分別為取復數的實部和虛部。

本文利用復振型疊加方法，位移向量x可展開為

(6)

(7)

在工程實踐中，通常關心的反應量有層位移、層間位移以及剪力、彎矩等，這些反應量是與位移相關的，故任意地震反應量R(t)=νTx(t)，ν為響應轉換向量，與結構的幾何、物理屬性有關。利用式(6)，R(t)可進一步表示為

(8)

式中：αi=νTρi；βi=νTφi。

(9)

式中，Vi與Di分別為第i階振型對應的速度譜值和位移譜值，為了使用的方便，通常速度譜由偽速度譜代替；ρvv,ij、ρvd,ij和ρdd,ij分別為振型速度-速度、速度-位移和位移-位移的振型相關系數，具有以下表達形式

(r=ωi/ωj)

(10)

(11)

(12)

式(7)即在一維地震作用下CCQC的表達形式，在引入相應的假定后可以將其進一步推廣到多維、多點地震激勵作用的情況。不過上述是基于線性系統推導而來，對于隔震結構需要提供隔震支座等效剛度，可以通過迭代確定。迭代步驟可詳見文獻[19]，如圖2所示。一般初始迭代位移在設防地震、罕遇地震作用下分別取100%、250%剪應變對應的位移值。

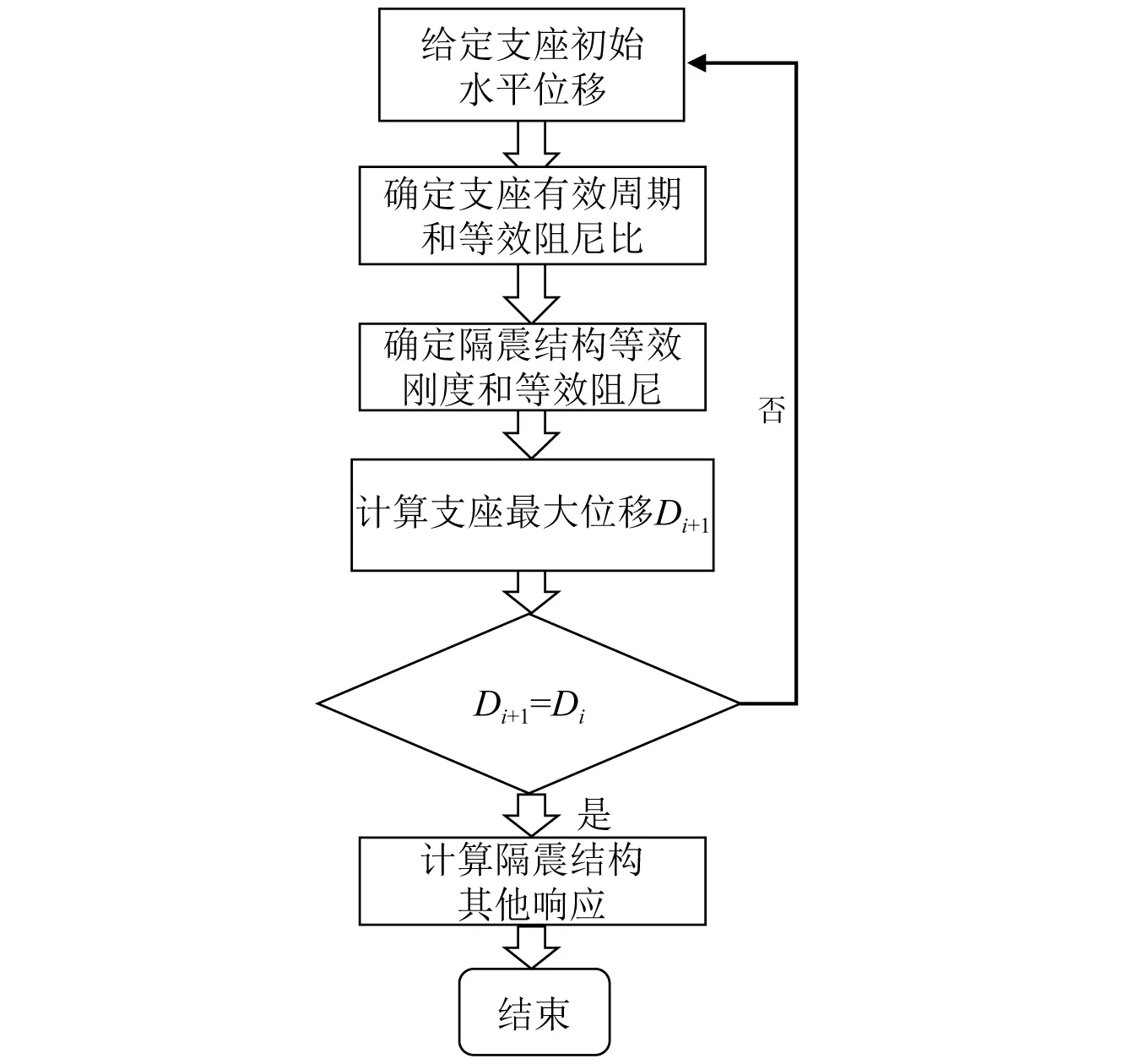
圖2 支座等效剛度、阻尼比的迭代方法

3 阻尼矩陣構造影響分析

針對第1章隔震結構模型，為方便生成非比例阻尼矩陣，將隔震層和上部結構看作兩個子結構。

3.1 分區瑞利阻尼方法

隔震層

cb=αbmb+βbkb

(13)

上部結構

Cs=αsMs+βsKs

(14)

式中：Ms、Ks分別為上部子結構質量和剛度矩陣；αb、βb、αs、βs分別為隔震系統子結構的瑞利阻尼比系數和上部子結構的瑞利阻尼比系數，由下式確定

(15)

(16)

ωi與ωj為對結構動力響應有顯著影響的最高和最低頻率。ξs、ξb分別為上部結構和隔震層的阻尼比。

此時隔震結構的整體非比例阻尼矩陣為

(17)

式中，cr為分區Rayleigh阻尼[20]，可得

cr=βs(-k1,0,…,0)

(18)

3.2 阻尼系數方法

圖1隔震結構為剪切型模型，上部結構阻尼可以取與剛度成比例，通過各層的阻尼比、剛度，求得各樓層的阻尼系數

(19)

然后按照剛度矩陣組集的方式來組裝整體的阻尼矩陣。求得整體阻尼如下式

3.3 瑞利-阻尼系數方法

對于隔震層上部結構可以采用瑞利阻尼形成阻尼矩陣，而對于隔震層或隔震支座則通過式(19)阻尼比換算成阻尼系數，然后按照剛度矩陣組集的方式來組裝整體的阻尼矩陣。

對隔震層，通過支座的等效阻尼比、等效剛度，求得阻尼系數

(20)

對于上部結構可按瑞利阻尼假定形成阻尼矩陣，即

Cs=αsMs+βsKs

(21)

式中：Ms、Ks分別為上部子結構質量和剛度矩陣；αi、βi分別為相應的質量和剛度比例系數，由下式確定

(22)

式中：ωm與ωn為整體結構中對應于上部結構第m、第n階自振頻率；ξm、ξn為相應振型阻尼比。

然后按照直接集裝兩個子結構方式來組裝整體的非比例阻尼矩陣。如式(23)所示。

(23)

3.4 振型疊加-阻尼系數方法

對隔震層，通過支座的等效阻尼比、等效剛度，求得阻尼系數

(24)

由于結構的各階振型的阻尼比呈現非線性分布，因此對上部結構可采用Clough提出另外一種阻尼模型

(25)

式中：Ms為上部結構質量矩陣；ωi、φi、Mi分別為自振頻率、無阻尼振型和振型質量。同樣按照直接集裝兩個子結構方式來組裝整體的非比利阻尼矩陣。

以10層剪切模型為研究對象，取剛度質量比k/m=1 767 s-2，所有振型的阻尼比為0.05。通過在結構底部更換不同參數的隔震層進行討論分析。

隔震層等效周期取為3 s。眾所周知，隔震結構第一階振型阻尼比主要由隔震層阻尼控制，高階振型阻尼比主要由上部結構阻尼控制。由圖3可知，當隔震層阻尼比大于0.05時，分區瑞利阻尼方法對隔震結構第一階振型阻尼比的反映不夠合理，遠小于隔震層等效阻尼比；瑞利-阻尼系數方法給出的第一階振型阻尼比稍大于隔震層等效阻尼比，但隨著隔震層阻尼比的增大，兩者越來越接近，特別需要指出的是，對于其他階振型阻尼比，這方法給出的數值明顯偏大，隨著振型階數的增大，阻尼比增大的程度也不斷加劇；振型疊加-阻尼系數方法和阻尼系數方法相對比較合理，兩者也非常接近，區別主要在于高階振型阻尼比，后者較大。

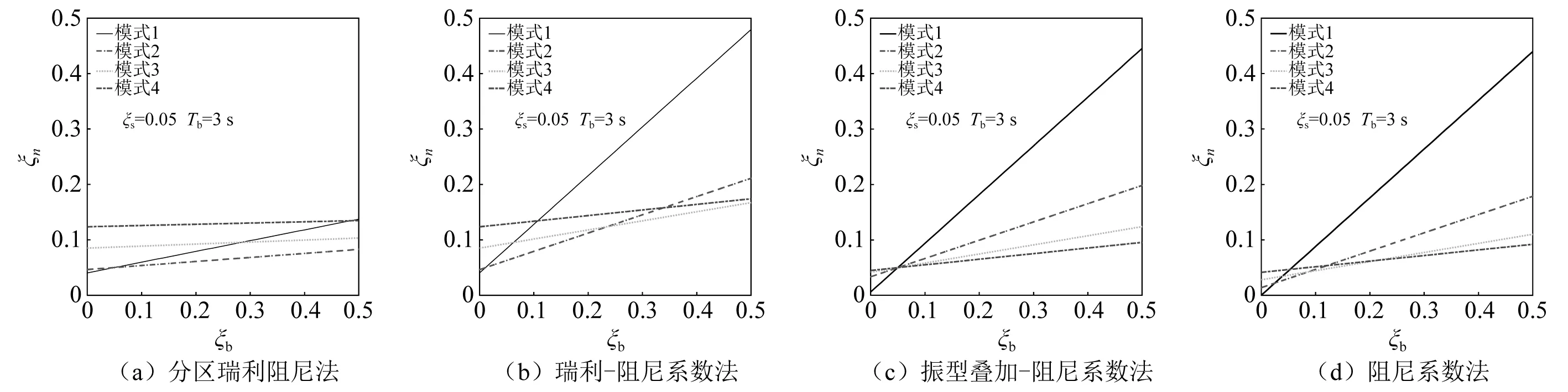
圖3 不同阻尼矩陣形成方式隨隔震層等效阻尼比變化對振型阻尼比的影響

不同阻尼矩陣形成方式隨隔震層等效周期Tb的變化對隔震結構振型阻尼比ξn的影響，如圖4所示。圖4中標注了前4階振型阻尼比變化曲線，其他曲線為第五～第十階振型阻尼比變化曲線。隨著隔震層等效周期Tb的增大，第一階振型阻尼比將趨近隔震層等效阻尼比。同時，其他階振型阻尼比也將越來越靠近上部結構阻尼比。對于這兩點規律，分區瑞利阻尼方法和瑞利-阻尼系數方法都沒有很好地表達出來(見圖4)。相對而言，振型疊加-阻尼系數方法和阻尼系數方法計算出的振型阻尼比隨隔震層等效周期的變化趨勢更為合理。

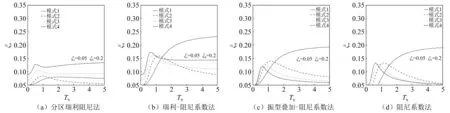
圖4 不同阻尼矩陣形成方式隨隔震層等效周期變化對振型阻尼比的影響

綜上所述，阻尼系數法和振型疊加-阻尼系數方法構造的隔震結構阻尼矩陣，無論是隔震層的阻尼變化，還是剛度變化，都能夠反應出隔震結構特性規律。然而分區瑞利阻尼的會對隔震一階振型進行抑制，對高階振型由會產生過阻尼現象，因此建議隔震結構采用振型疊加-阻尼系數和阻尼系數方法進行結構阻尼矩陣的構造。

4 結構算例分析

以一典型的10層框架剪切模型為研究對象，層質量m與層剛度k均勻分布，取剛度質量比k/m=1 767 s-2使得結構基本周期為1 s，所有振型的阻尼比為0.05。在結構底層增加隔震層，如圖5所示。

圖5 隔震結構分析模型

4.1 基于近、遠地震波反應譜分析

為了得到阻尼矩陣形成方式對反應譜CQC與反應譜CCQC兩種方式計算方式的影響，避免由于反應譜計算(速度反應譜估計、阻尼修正系數)引起的影響，從而采用天然波的反應譜比較系統的研究阻尼矩陣形成方法、隔震層等效阻尼比、等效剛度、地震動特性對兩種方法精度的影響。在這方式中，地震動記錄選取ATC-63推薦的28組近場地震和22組遠場地震，其中把每組地震動加速度峰值最大的分量調至0.4g。

兩組地震作用下采用不同阻尼矩陣形成方法上部結構底部剪力隨隔震層等效阻尼比的變化曲線，如圖6、圖7所示。每幅圖中，隔震層等效周期為3 s，“TimeHistory”表示基于時程分析的所有地震動作用下最大基底剪力的平均值Vb，“CQC”表示對每一條地震動反應譜進行強迫解耦的CQC組合后取平均，“CCQC”表示對每一條地震動反應譜進行強迫解耦的CCQC組合后取平均。此外，所有的基底剪力通過阻尼系數方法求得的隔震層等效阻尼比為0時的基底剪力進行標準化。

由圖6、圖7可知，在隔震層阻尼比小于0.05時，“TimeHistory”、“CQC”和“CCQC”計算出的基底剪力重合時，說明隔震層阻尼的非比例影響可以忽略，這時可以采用任意一種阻尼矩陣構造方法。當隔震結構阻尼大于0.05時，4種阻尼構造方式結構分區瑞利阻尼方法得到結果與其他3種方法差別最大，沒有反映出非比例阻尼的影響。除數值大小有差別外，瑞利-阻尼系數方法、振型疊加-阻尼系數方法、阻尼系數方法得到的基底剪力隨隔震層阻尼的變化趨勢基本一致。隔震結構基底剪力與構件內力大小息息相關，隔震結構阻尼比一般在0.1～0.3，在此范圍內阻尼系數方法反映出的結構基底較大。由此可知，進行隔震結構設計時，并且結構阻尼比大于0.05時，優先選用阻尼系數方法較為合理。

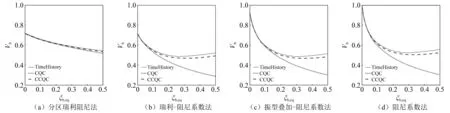
圖6 近場地震作用下阻尼矩陣形成方式對結構響應的影響

圖7 遠場地震作用下阻尼矩陣形成方式對結構響應的影響

通過上述研究發現阻尼系數方法更適合用于隔震結構的阻尼矩陣構造，在此基礎上為探究兩種方法的計算精度，在后面的計算中統一采用阻尼系數方法來形成阻尼矩陣。取隔震層等效周期為3 s，下標“rsm”表示反應譜方法CQC或CCQC，“thm”表示時程分析方法。對于每一條地震動按照CQC、CCQC和時程分析方法分別計算結構響應，然后以時程分析結果為基準得到CQC和CCQC的相對誤差，最后將所有地震動作用下的計算誤差進行平均示于圖中。圖8～圖11中，同一種方法的計算結果用同一種線型表示，每一種方法包含若干條曲線，對應各個樓層的地震響應計算誤差。

圖8 近場地震作用下CQC與CCQC對比

兩組地震作用下，CQC與CCQC的計算精度隨隔震層等效阻尼比的變化如圖8、圖9所示。可以發現，對于上部樓層位移，當結構隔震層阻尼比ξb,eq在0.05以內時，兩種方法精度相當，可以選擇任意一種。然而隔震結構阻尼比一般在0.1～0.3，從圖8、圖9中可以發現在此區間范圍，CQC預測結果稍偏小；對于層間剪力，CQC預測結果偏小較多，此時不能選擇CQC方法。若將計算精度控制在±10%以內的話，CQC的適用范圍依然在0.05以內，即非隔震結構。此外，可以發現近場地震作用下的CQC計算誤差顯著大于遠場地震作用。這是因為近場地震相對遠場地震強度更大，并且具有脈沖效應，進一步說明CQC方法對遠場、近場地震作用比較敏感，采用此方法前，應對地震波的選取更加謹慎。而CCQC方法無論在遠場還是近場地震下，誤差波動小且預測精度較好。

圖9 遠場地震作用下CQC與CCQC對比

取隔震層等效阻尼比為20%，兩組地震作用下，CQC與CCQC的計算精度隨隔震層等效周期的變化如圖10、圖11所示。可以發現，對于樓層位移，隨著隔震層有效周期的增大，CQC與CCQC的計算精度得以提高，CCQC預測值始終比CQC稍大；對于樓層剪力，隨著隔震層有效周期的增大，CQC的計算誤差也越來越大，近場地震作用下更為顯著。結合上述，可以發現CQC反應譜方法會嚴重低估隔震結構的樓層剪力，從而會對結構設計產生重大影響，而近場地震作用下，CQC方法預測誤差會加大，因此建議在對結構進行隔震設計時，考慮采用CCQC方法。在使用CQC方法時不僅需要考慮結構的阻尼比范圍，還需要同時進行近、遠場地震作用分析，以便確定安全設計方案。

圖10 近場地震作用下CQC與CCQC對比

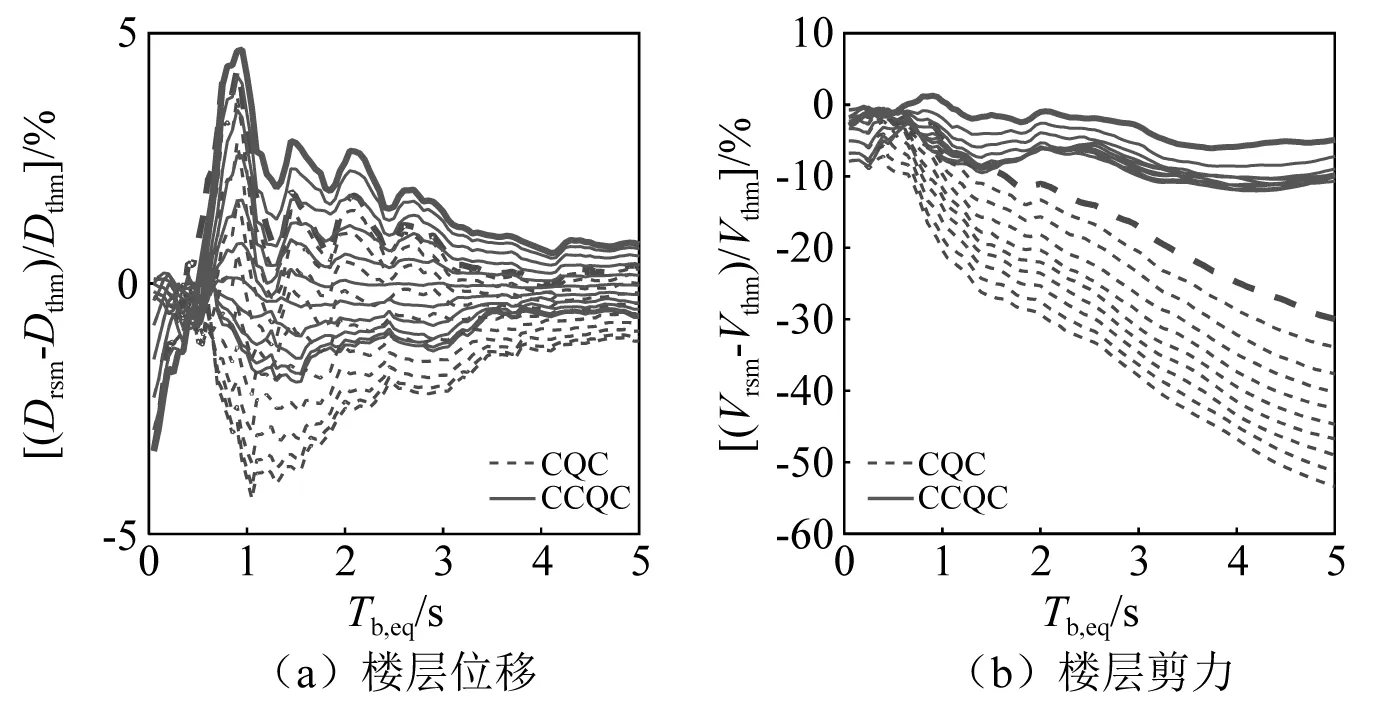
圖11 遠場地震作用下CQC與CCQC對比

4.2 設計反應譜分析

對于隔震結構第一階振型阻尼比遠大于5%，而高階振型阻尼比又有可能小于5%。阻尼比為2%、5%、10%、20%、30%時規范設計反應譜與人工加速度平均反應譜的對比，如圖12所示。圖12中相同阻尼比的規范譜和設計反應譜采用相同的線型和顏色。由圖12可知，隨著阻尼比的增大，設計反應譜與人工加速度平均反應譜的差別越來越大，而且人工加速度平均反應譜值在整個周期段普遍偏小。可以預測隔震層阻尼比越大，基于設計反應譜的反應譜方法計算結果將越大于時程分析結果。這是由人工加速度時程不能兼容多阻尼比目標譜導致的，因此本文人工波生成采用隔震層阻尼比修正的設計反應譜為目標譜。

圖12 不同阻尼比規范設計反應譜與人工加速度平均反應譜

在工程實踐中，不論是CQC方法還是CCQC方法都需要基于設計反應譜進行峰值響應組合，因此分析此種情況下的CQC與CCQC方法的特性更具有實用意義。為與時程分析結果對比，以設計反應譜為目標譜，采用時域內余弦調幅的方法生成30條人工加速度時程的反應譜以及與設計反應譜對比，如圖13所示。

圖13 30條人工波反應譜及其平均值與規范設計反應譜間的對比

采用3種方法進行動力響應分析，即反應譜方法CQC、CCQC和時程分析方法。CQC(code spectra)、CCQC(code spectra)分別表示在基于強迫解耦的CQC組合和CCQC組合中采用設計反應譜；需要指出的是，CCQC(code spectra)中，速度反應譜由(偽加速度)設計反應譜轉換成的偽速度反應譜近似，對于阻尼比的譜值由抗震規范提供的阻尼修正系數來調整。CCQC(synthetic acc spectra) 表示CCQC組合中采用由30條人工加速度時程計算出的平均位移反應譜和速度反應譜。上述3種反應譜方法求得的結構響應以下標“rsm”表示，下標“thm”表示時程分析得出的平均結構響應。所有計算出的結果，以時程分析結果為基準，進行對比，分析不同計算方法的精度。圖14、圖15中，同一種方法的計算結果用同一種線型表示，每一種方法包含若干條曲線，對應各個樓層的地震響應。

圖14 隔震層等效阻尼比對CQC與CCQC計算精度的影響

圖15 隔震層等效周期對CQC與CCQC計算精度的影響

首先，假定隔震層等效周期Tb,eq=3 s，研究隔震層等效阻尼比ξb,eq對CQC與CCQC計算精度的影響，如圖14所示。圖14(a)為3種反應譜方法樓層位移誤差，CCQC(synthetic acc spectra)精度最高，CQC(code spectra)與CCQC(code spectra)結果非常接近，但隨著隔震層等效阻尼比的增大，計算結果越來越大。因此，在常用的隔震層等效阻尼比在0.1～0.3內，采用基于設計反應譜的CQC或CCQC方法預測的樓層位移(包括隔震層位移)稍偏于保守。而對于樓層剪力、樓層傾覆彎矩CQC(code spectra)與CCQC(code spectra)差別非常顯著，同樣在ξb,eq在0.1～0.3內，所有樓層CCQC(code spectra)的精度在-10%～10% (負號表示小于時程結果)，CQC(code spectra)在-1%～-40%內，而且其各個樓層計算誤差較為分散，樓層位置越高誤差越大。圖中實線為CCQC(synthetic acc spectra)，是用真實的反應譜值進行組合，但樓層剪力和樓層傾覆彎矩比時程結果稍小，在10%以內。綜合上述所言，當結構阻尼在0.05以內， CQC和CCQC反應譜方法預測結構響應都偏小，此時建議采用CCQC(synthetic acc spectra)，較為精準。當隔震結構等效阻尼比處于0.1～0.3時，采用CCQC反應譜方法最為保守，符合我國的設計思想。

假定隔震層等效阻尼比ξb,eq=20%，研究隔震層等效周期Tb,eq對CQC與CCQC計算精度的影響，如圖15所示。當隔震層等效周期小于1 s時，對結構響應起主導作用的振型阻尼比均在5%以下，而此時人工加速度平均反應譜在周期0～1 s段大于設計反應譜值，從而導致在隔震層等效周期小于1 s的區域內，時程結果大于基于設計反應譜的CQC、CCQC計算結果。由于上部結構基本周期為1 s，通常隔震之后的基本周期遠大于1 s。因此，本文主要關注隔震層等效周期大于1 s的情況。對樓層位移，基于設計反應譜的CQC與CCQC方法非常接近，同時隨著隔震層等效周期的增大，計算結果也不斷增大，如圖15(a)所示。而對于樓層剪力和傾覆彎矩在2～4 s，基于設計反應譜的CQC與CCQC方法差別較大，從圖15可知，基于設計反應譜的CCQC方法計算結果均大于時程分析結果，而基于設計反應譜的CQC方法計算結果明顯偏小，特別是較高樓層位置，而且隨著隔震層等效周期的增大，這種偏小的程度進一步加劇。此外，對于紅色曲線表示的基于人工加速度平均反應譜的CCQC方法，其計算出的樓層剪力比時程結果稍小，但隔震層等效周期對其影響不大。因此當隔震結構周期處于2 s以上時，建議采用CCQC方法。

5 結 論

本文通過4種不同構造方式形成整體非比例阻尼矩陣，并在此基礎上分析了一些參數對復振型分解反應譜方法的計算影響，現得出結論如下：

(1) 分區瑞利阻尼不能合理反映隔震結構一階振型阻尼比，并且隨著隔震層等效阻尼比和周期變化，分區瑞利阻尼不能體現非比例阻尼特性對上部結構底部剪力影響。阻尼系數方法得到響應較其他方法大，所以在實際應用中，建議阻尼矩陣采用阻尼系數方法或振型疊加方法進行組裝。

(2) 近場地震作用下，隔震層阻尼在20%內時，CCQC和CQC方法精度相當。但對于樓層剪力，CCQC比較平穩，且精度在10%內；CQC方法隨等效阻尼比變大而逐漸偏小，誤差在10%～70%，可以看出隔震層阻尼容易引起上部結構響應放大，CQC方法不能反映出這一特點。

(3) 基于設計反應譜的CQC方法在常用的隔震層等效阻尼比0.1～0.3、等效周期2～4 s內，上部樓層剪力、樓層傾覆彎矩偏低，特別是頂層剪力偏小20%～30%；基于設計反應譜的CCQC方法進行隔震設計較CQC方法安全。

(4) CQC方法計算誤差的大小除了與隔震層等效阻尼比有關外，還受地震動特性、隔震層等效周期、計算中采用的阻尼矩陣形式等因素影響。因此，規定一個具體的隔震層等效阻尼比作為CQC方法的適用性判別指標是不恰當的。而CCQC方法更具一般性。