三參數Pasternak黏彈性地基中錐形樁的橫向自由振動特性研究

張金輪， 張阿祥， 葛仁余， 孫俊偉

(安徽工程大學 建筑工程學院, 安徽 蕪湖 241000)

錐形樁的楔型構造改變了樁周土的天然結構狀態，可改善土的物理力學性質，有利于提高其承載力[1]，適用于一般土層結構[2]，具有顯著的技術經濟效果。我國于20世紀70年代已將圓錐形樁、正方錐形樁及矩形楔形樁等漸變截面樁應用于實踐[3]，由于對其承載特性及樁身側面與樁周土相互作用的機理研究還不夠充分，使得在設計使用時尚無對應的規范和計算方法，因而限制了其推廣應用[4]。隨著理論方法與試驗技術的進步，相關變截面樁的動力特性研究逐漸受到關注[5-6]。單樁自振頻率是其動力分析的基本參數，與地基的物理力學指標、樁的幾何力學性質、質量分布情況及樁端約束條件等因素有關[7]。關于單樁自由振動特性的相關理論與數值研究，Yesilce[8]僅考慮地基彈性剛度的影響，利用微分變換法和微分求積元法對彈性地基上半剛體連接的Reddy-Bickford型矩形梁的橫向自由振動特性進行分析。王奎華等[9]基于廣義Voigt模型，在考慮樁身阻尼情況下，應用阻抗傳遞法及Laplace變換技術研究了成層土體中帶明置承臺單樁的縱向自由振動問題，給出了自由振動位移的半解析解，但并沒有對樁的自振頻率及其衰減系數進行具體分析。彭麗等[10-11]應用復模態方法研究了三參數黏彈性地基上等截面梁的橫向自由振動特性，該法需求解超越方程使計算變得復雜。Mohammadimehr等[12]利用微分求積方法研究了三參數Pasternak黏彈性地基上錐形黏彈性微桿的橫向自由振動特性。Ma等[13]對樁的臨界荷載和屈曲結構進行解析求解，討論了地基彈性剛度與剪切剛度對單樁的屈曲響應和自由振動特性的影響，但并未考慮地基阻尼的作用。柳偉等[14-15]基于Timoshenko梁理論的Winkler地基模型，運用回傳射線矩陣法及求根法研究了黏彈性地基中單樁的外露長度、埋置深度、樁端約束情況對其縱-橫向耦合自由振動各階自振頻率及其衰減系數與振型的影響，但未考慮地基剪切剛度的作用。Zhang等[16]基于Timoshenko梁理論，應用插值矩陣法研究了三參數Pasternak黏彈性地基上錐形梁的橫向自由振動特性，將地基參數設為常量分析了兩端簡支邊界下錐度系數與地基阻尼對梁固有頻率的耦合效應。基于Euler-Bernoulli理論，Lee等[17]考慮長圓錐形摩擦樁的樁側均布摩阻力與樁周土地基彈性剛度沿樁身的變化，建立了一種求解非均質彈性地基中錐形樁的固有頻率和振型的理論模型；Liu等[18]同時考慮樁周土的線性軸向摩擦和線性側移剛度，通過近似解析方法研究了非均質彈性地基中圓錐形摩擦樁的屈曲特性；但均未考慮樁周土阻尼與剪切剛度的影響。綜上所述，目前考慮黏彈性地基中錐形樁有阻尼橫向自由振動特性的研究鮮見報道。

本文在Zhang等研究的基礎上，將樁體簡化為線彈性錐形Timoshenko梁-柱，考慮圓截面錐形樁樁徑沿縱向線性變化引起樁側摩阻力與樁周土地基參數沿樁身縱向連續分布的不均勻性，提出三參數Pasternak黏彈性地基中錐形樁的動力學模型，利用微元體的平衡條件建立其振動控制方程，應用微分求積法與QR法求解該樁-土體系的橫向自由振動響應。通過算例，分析了相應邊界條件欠阻尼狀態下樁身錐角、地基阻尼、地基橫向彈性剛度與剪切剛度、樁側摩阻力、軸向荷載、樁長徑比等參數對其橫向自由振動頻率特性的影響。

1 錐形樁-土體系動力學模型及控制方程

1.1 基本假定及計算模型

結合現有研究成果，為便于建立方程，做以下基本假定：①將錐形樁簡化為線彈性錐形Timoshenko梁-柱，即同時考慮樁橫截面彎矩變形、剪切變形與轉動慣量的影響；②樁周土土質均勻、各向同性，視為黏彈性連續介質，采用三參數Pasternak黏彈性地基模型模擬樁周土；③考慮樁-土相互作用受樁徑大小的影響，假定樁側摩阻力與各地基參數自樁頂至樁底均與樁徑呈等比例線性變化，形成樁-土體系的計算模型，如圖1所示。

圖1 樁-土體系的計算模型

圖1中：樁長為l；x為橫向坐標；z為從樁頂沿豎向的坐標；t為時間；P為承臺傳遞的軸向荷載。設任意z處截面中性軸上的橫向位移為u(z,t)，截面彎曲轉角為φ(z,t)；樁的彈性模量為Ep、質量密度為ρp、剪切模量為Gp、泊松比為νp、截面剪切修正系數為κ，均為常量，且有Gp=Ep/[2(1+νp)]；樁橫截面的周長、面積與慣性矩分別用up(z)、Ap(z)與Ip(z)表示，均為關于z的連續可微函數，設up(z)=up0h1(z)，Ap(z)=Ap0h2(z)，Ip(z)=Ip0h3(z)，up0、Ap0、Ip0對應于樁頂橫截面的周長、面積與慣性矩。對于圓錐形樁，其截面幾何性質描述如下式

(1)

式中：d0為樁頂截面直徑；m為描述截面幾何性質變化的錐度系數，且0≤m<1。設錐形樁錐角為θ，樁頂截面半徑為r0，則有：m=tanθ·l/r0。可知，當m值為零時，表示為等截面樁；當l/r0值一定時，m值越大，反映錐形樁的錐角越大。

圖1(a)中，φ、γ、α分別為樁身微元段中性軸由純彎矩引起的轉角、由純剪力引起的剪切角、由彎矩和剪力共同作用引起的轉角，且φ=α-γ。圖1(b)中：M(z,t)、Q(z,t)、N(z,t)分別為樁身任意深度z處橫截面上的彎矩、剪力與軸力；fI(z,t)為由橫向振動引起的單位長度橫向慣性力；mI(z,t)為由橫向振動引起的單位長度轉動慣性力矩；Rs(z,t)為樁周土的地基反力。由Timoshenko梁理論可得如下關系[19]

(2)

(3)

(4)

(5)

設任意深度z處，軸向力N(z,t)始終與樁軸線方向相切，且不計樁自質量對軸向力的影響，N(z,t)>0表示為軸向壓力；樁-土界面處的摩擦力用單位摩阻力f(z)表示，假定樁側摩阻力隨深度均勻線性變化，即

(6)

式中：f0為樁頂位置處對應的樁側摩阻力；n1為比例系數。則深度z處樁橫截面上的軸向力表示為

(7)

將式(1)的第1項與式(6)代入式(7)，得

P-f0up0lh4(z)

(8)

式中，h4(z)為關于z的連續可微函數;可知，當f0=0時表示樁身不考慮土的豎向摩擦力影響，為端承樁。

由前述基本假定可得，微元體變形后，橫截面上的水平向力H(z,t)與剪力Q(z,t)及軸向力N(z,t)的關系為[20]

(9)

土層任意深度z處，設樁周土模型的橫向彈性系數、阻尼系數與剪切系數分別用k(z)、c(z)和g(z)表示。由三參數Pasternak黏彈性地基模型，可知

(10)

根據基本假定式(3)，可設

(11)

式中：k0、c0、g0分別為樁頂位置處對應的地基橫向彈性系數、阻尼系數與剪切系數，分別反映樁周土的地基橫向彈性剛度、阻尼效應與剪切剛度對樁身的作用；n2、n3、n4為比例系數。

1.2 錐形樁橫向自由振動控制方程及邊界條件

根據圖1(b)微元段變形后的動力平衡條件即截面橫向受力與彎矩的平衡，結合式(2)～式(5)、式(9)、式(10)，推導出錐形樁橫向自由振動的控制方程為

(12)

將式(1)、式(8)、式(10)、式(11)代入式(12)，整理得

(13)

考慮自由振動問題，可設

u(z,t)=U(z)eλt,φ(z,t)=Φ(z)eλt

(14)

式中：U(z)、Φ(z)分別為樁身橫向位移和截面彎曲轉角的振型函數；λ為錐形樁的特征復頻率；e為自然底數。

將式(14)代入式(13)，則通過分離變量消除eλt項后，樁的橫向自由振動控制方程轉化為下式

(15)

(16)

式(16)中系數項含有Ω2項，為便于求解方程組，引入2個新的變量函數Y1(ξ)、Y2(ξ)，即

(17)

將式(17)代入式(16)，并聯立得如下方程組

(18)

為便于描述本文方法的求解過程，引入下列系數參量代入式(18)得式(19)。

(19)

式中：g(ξ)為方程組中不含特征值Ω的系數項；q為含特征值Ω的系數項；g(ξ)與q的第1個下標為微分方程組的方程，3為第3個方程，4為第4個方程；第2個下標為微分方程組中相應的函數，1為Y1(ξ)，2為Y2(ξ)，3為W(ξ)，4為Φ(ξ)；第3個下標為對應函數的導函數階數，1為函數的一階導數，2為函數的二階導數。

關于樁端的邊界條件，下面對固支(C)、鉸支(H)、約束轉角(P)和自由(F)4種邊界約束條件對應的方程進行描述。

(1)對于固支邊界條件，z=0或l位置：u(z,t)=0，φ(z,t)=0。無量綱化后，ξ=0與ξ=1處的邊界條件方程為

(20)

(2)對于鉸支邊界條件，z=0或l位置：u(z,t)=0，M(z,t)=0。無量綱化后，ξ=0與ξ=1處的邊界條件方程為

(21)

(3)對于約束轉角邊界條件，z=0或l位置：H(z,t)=0，φ(z,t)=0。無量綱化后，ξ=0與ξ=1處的邊界條件方程為

(22)

(4)對于自由邊界條件，z=0或l位置：H(z,t)=0，M(z,t)=0。無量綱化后，ξ=0與ξ=1處的邊界條件方程為

(23)

至此，軸向荷載作用下黏彈性地基中錐形樁橫向自由振動的固有頻率及其對應振型函數求解問題，已經轉化為求解滿足相應邊界條件方程式(20)～式(23)的變系數常微分方程組式(19)的一次特征值及其特征向量問題。

2 振動控制方程的微分求積法求解

由于錐形樁-土體系的振動控制方程式(19)及邊界方程式(20)～式(23)中均含有變系數項，該類問題很難獲得解析解，本文采用微分求積法進行數值解析。鑒于微分求積法對節點的離散形式較為敏感，基于數學角度，選取靠近邊界的節點步長逐步減小的分布形式對減少權系數的截斷誤差、提高計算精度有利；基于力學角度，如剛度在端部附近區域發生突變或由于端部邊界條件的影響，使得端點附近成為位移和內力變化最敏感的區域，在端部區域布置較多細密非均勻節點同樣利于計算精度的提高。因此，本文采用非均勻分布的等比數列節點離散形式對ξ∈[0,1]區間進行節點變步長設置，如圖2所示，對應節點離散公式如下[21]

圖2 樁的離散模型

(24)

式中:ξi∈[0,1]，區間分段數n取為偶數，q1為調節節點步長的公比，可根據邊界條件與計算精度的需要調整，Zhang等給出了q1的合理取值范圍，并驗證了該類型節點與微分求積法中常用的以切比雪夫多項式根為節點具有相同的幾何特征和計算精度。本文相關數值計算均取n=32,q1=1.2，后面不再贅述。

根據微分求積法原理，函數W(ξ)、Ф(ξ)在各節點上的導函數值可用(n+1)個節點對應函數值的加權線性求和來近似表示。函數及其相應導函數在各節點處的函數值用拉格朗日插值表示為

(25)

式中，lj(ξ)為拉格朗日插值多項式，即

(26)

對式(25)函數W(ξ)、Ф(ξ)分別求一階導數，得

(27)

將式(27)中的ξ離散化，可知

(28)

依次類推，則

i,j=0,1,2,…,n

(29)

(30)

式(29)用向量形式表示為

(31)

W(r)(ξi)={W(r)(ξ0),W(r)(ξ1),…,W(r)(ξn)}T，

W(ξj)={W(ξ0),W(ξ1),…,W(ξn)}T，

Φ(r)(ξi)={Φ(r)(ξ0),Φ(r)(ξ1),…,Φ(r)(ξn)}T，

Φ(ξj)={Φ(ξ0),Φ(ξ1),…,Φ(ξn)}T，

由函數微分關系

(32)

可得，函數各階導數的加權系數矩陣之間的關系如下

(33)

將振動控制方程式(19)數值離散，并用向量形式表示，方程中的變系數項寫成對角陣形式，即

G332=diag{g332(ξ0),g332(ξ1),…,g332(ξn)},

G331=diag{g331(ξ0),g331(ξ1),…,g331(ξn)},

G330=diag{g330(ξ0),g330(ξ1),…,g330(ξn)},

G340=diag{g340(ξ0),g340(ξ1),…,g340(ξn)},

G310=diag{g310(ξ0),g310(ξ1),…,g310(ξn)},

G431=diag{g431(ξ0),g431(ξ1),…,g431(ξn)},

G441=diag{g441(ξ0),g441(ξ1),…,g441(ξn)},

G440=diag{g440(ξ0),g440(ξ1),…,g440(ξn)},

Q310=diag{q310,q310,…,q310},

Q420=diag{q420,q420,…,q420}

結合式(31)、式(33)，將振動控制方程式(19)轉化為向量矩陣形式如下

(34)

關于邊界條件的處理，不失一般性地以樁頂約束轉角、樁底固支邊界條件(P-C)為例，對應邊界條件方程的向量形式可寫為

(35)

式中，[…]L為矩陣[…]的第L行元素。

式(34)由4個最高階導函數為2階的代數方程組成，可采用直接法引入式(35)中的4個邊界條件方程。具體做法是分別用式(35)第1式中向量W前的行元素替換式(34)第3式中矩陣B的第1行元素，向量Ф前的行元素替換矩陣C的第1行元素、第3式的其余系數項矩陣的第1行元素均用數值0替換；用式(35)第2式中向量Ф前的行元素替換式(34)第4式中矩陣E的第1行元素，第4式的其余系數項矩陣的第1行元素均用數值0替換；用式(35)第3式中向量W前的行元素替換式(34)第3式中矩陣B的第(n+1)行元素，第3式的其余系數項矩陣的第(n+1)行元素均用數值0替換；用式(35)第4式中向量Ф前的行元素替換式(34)第4式中矩陣E的第(n+1)行元素，第4式的其余系數項矩陣的第(n+1)行元素均用數值0替換。

(36)

式(36)為含有(4n+4)個未知向量的一般線性代數特征方程組，進而應用QR分解技術進行數值計算，可同時得到一系列特征值Ω及其對應特征向量Y1、Y2、W、Φ，且均為復數形式。其中：Ω即為錐形樁的無量綱特征復頻率；W、Φ為其對應的橫向位移與彎曲轉角的復振型，相應振型的虛部與實部分別用WI、WR與ΦI、ΦR表示。

3 算例與討論

根據第2章微分求積法求解黏彈性地基中錐形樁橫向自由振動控制微分方程組的方案，采用FORTRAN語言編制計算機程序進行數值計算，并在1 s以內完成相應問題的求解。下面先通過2個已知結果的算例驗證目前方法的適用性，進一步分析各相關參數及比例系數對樁固有特性的影響。

3.1 數值算例對比驗證

3.1.1 等截面Timoshenko梁的橫向自由振動

當式(16)中無量綱參量m=β=k=c=g=0時，模型退化為等截面Timoshenko梁的橫向自由振動問題。表1列舉了當無量綱參量r=0.01、s=0.031 2、p=0時，不同邊界條件下等截面Timoshenko梁前5階無量綱固有頻率。由表1可知，本文解與Tang等的精確解幾乎完全吻合，驗證了目前方法在求解不同邊界條件下等截面Timoshenko梁橫向自由振動固有頻率良好的適用性與高精度。此外，與Zhang等的解相比，本文方法的區間分段數n明顯較小，求解一般線性代數特征方程組矩陣的階數為132×132，而Zhang等的解為324×324。可見，在達到同等精度條件下，目前方法的計算效率優于Zhang等的解。

表1 不同邊界下，等截面Timoshenko梁橫向自由振動前5階固有頻率(r=0.01, s=0.0312, p=0)

3.1.2 黏彈性地基上錐形梁的橫向自由振動

當不考慮樁-土界面摩擦力影響，且樁周土的地基參數沿樁縱向為常量即式(16)中無量綱參量β=0,n1=n2=n3=n4=0時，模型退化為三參數Pasternak黏彈性地基上錐形Timoshenko梁的橫向自由振動問題，梁的幾何性質同式(1)。表2列舉了無量綱參量r=0.002 5,s=0.012 5,p=0.25,k=2.5,g=0.246時，不同邊界條件下梁的前3階無量綱固有頻率及對應衰減系數，并與Zhang等的研究進行對比，相關數值結果高度吻合。可見，目前方法適用于求解三參數黏彈性地基上變截面Timoshenko梁的橫向自由振動問題。此外，由表2可知，邊界條件、錐度系數與地基阻尼系數對梁的各階固有頻率及其衰減系數均有較大影響；相同參數下，梁的各階頻率相差較大，而衰減系數相差相對較小。

表2 不同邊界下，三參數Pasternak黏彈性地基上錐形Timoshenko梁橫向自由振動前3階固有頻率及其衰減系數(r=0.002 5, s=0.012 5, p=0.25, k=2.5, g=0.246; n=32, q1=1.2)

3.2 黏彈性地基中錐形樁橫向自由振動特性分析

參照文獻[22-23]進行樁-土體系的參數取值，設均質黏彈性地基中，圓截面錐形樁的彈性模量Ep=2.0×1010N/m2，質量密度ρp=2.5×103kg/m3，泊松比νp=0.17，樁頂截面半徑r0=d0/2=0.15 m，樁長l=1.8 m，截面剪切修正系數κ=0.75；樁周土的彈性模量Es=4.0×106N/m2，質量密度ρs=2.0×103kg/m3，泊松比νs=0.4。參照Liu等的研究，取樁頂處樁側摩阻力的初值f0=100 kPa；取樁頂承受軸向壓力的初值為P=100 kN；考慮樁頂平臺的影響，將樁頂邊界條件近似為轉角約束。對應地基參數，k0按經驗公式取值[24]，即

k0=1.2Es

(37)

根據文獻[25]提供的c0參數建議取值范圍，確定無量綱參數c的取值范圍為[0, 0.1]；設無量綱參數g的值范圍為[0, 0.1]，當g=0時，樁周土模型退化為動力Winkler模型。根據上述已知條件，相應無量綱參數為：r=1.736×10-3,s=5.417×10-3,p=2.207×10-4,β=3.744×10-4,k=0.034 3 , 取初值c=g=0.02。在具體數值計算中，為便于參數分析，由樁側摩阻力隨楔角增大而增大，取比例系數n1=-m；由Voigt體的彈性系數、粘壺系數與樁徑成正比[26]，取比例系數n2=n3=n4=m。

表3給出了3種邊界條件下，錐度系數m=0和m=0.5時樁的前5階無量綱固有頻率及其衰減系數。其中，固有頻率為欠阻尼自振頻率；對應衰減系數為負值反映了地基阻尼對樁位移輸出響應的衰減特性，數值越小，位移振幅衰減越快。由表3可知：樁頂約束轉角時，固有頻率隨樁底約束的減弱明顯降低，而對應衰減系數小幅增大；樁頂直徑相同時，錐形樁較等截面樁的固有頻率降低，而對應衰減系數增大，描述了樁身沿縱向逐漸變柔后固有特性的顯著變化；相同參數時，各階固有頻率相差較大，而衰減系數相差微小，反映本文錐形樁-土體系可近似視為比例阻尼系統。

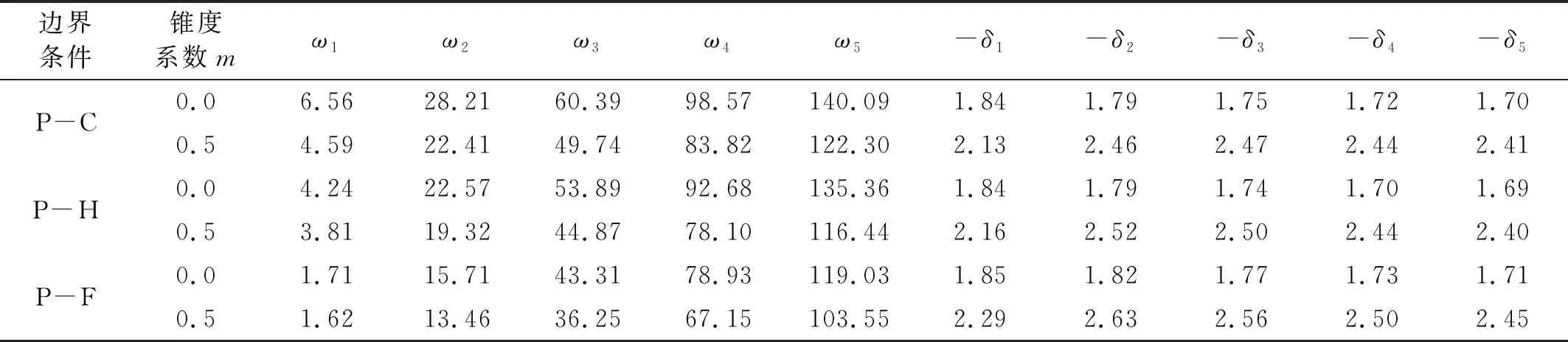
表3 不同邊界下，樁的前5階無量綱固有頻率及其衰減系數(r=1.736×10-3, s=5.417×10-3, p=2.207×10-4, β=3.744×10-4, k=0.034 3, c=g=0.02; n1=-m, n2=n3=n4=m)

3.2.1 錐角與地基阻尼對樁固有特性的影響

由式(1)可知，當樁長與樁頂截面半徑之比l/r0不變時，錐形樁的錐角與錐度系數成正比，可通過調整錐度系數m值分析錐角θ對樁固有頻率及其振型的影響。

圖3、圖4分別描述了欠阻尼狀態下，3種邊界條件樁前2階固有頻率及其衰減系數隨錐度系數在[0, 0.85]內變化的關系曲線。由圖3可知：樁頂約束轉角時樁底約束越強，基頻越大，對應衰減系數越小；基頻及其衰減系數均隨錐度系數的增加而降低，且降幅受邊界條件影響顯著，P-C邊界基頻降幅最大而衰減系數降幅相對較小，P-H邊界基頻降幅較小而衰減系數降幅居中，P-F邊界基頻降幅最小而衰減系數降幅相對較大。由圖4可見：P-C邊界與P-H邊界第2階固有頻率均隨錐度系數的增加而降低，P-C邊界降幅較大，而P-F邊界隨錐度系數的增加先降后增；3種邊界第2階衰減系數均隨錐度系數的增加呈明顯的非線性降低。結合圖3與圖4來看：考慮到常見錐形樁的楔角小于2°即當m≤0.5時，固有頻率及其衰減系數隨楔角的增加而降低，數值上該降幅2階高于1階，且受邊界條件影響較大。

圖3 不同邊界下，樁第1階無量綱固有頻率及衰減系數隨錐度系數的變化關系曲線(r=1.736×10-3, s=5.417×10-3,p=2.207×10-4, β=3.744×10-4, k=0.034 3, c=g=0.02; n1=-m, n2=n3=n4=m)

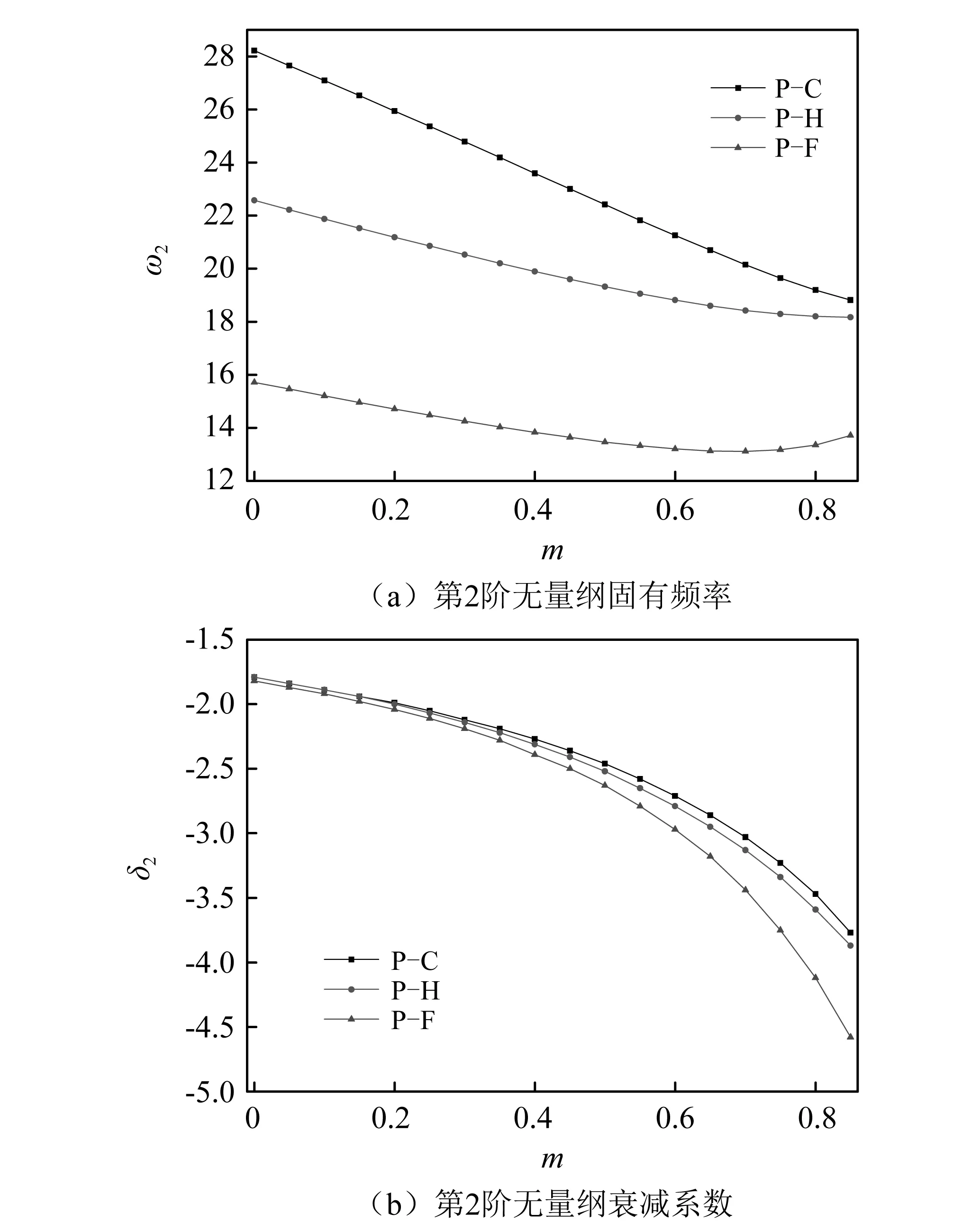
圖4 不同邊界下，樁第2階無量綱固有頻率及衰減系數隨錐度系數的變化關系曲線(r=1.736×10-3, s=5.417×10-3, p=2.207×10-4, β=3.744×10-4, k=0.034 3, c=g=0.02; n1=-m, n2=n3=n4=m)

以P-C邊界為例，圖5、圖6分別刻畫了等截面樁(m=0)與錐形樁(m=0.5)前3階樁身截面橫向位移與彎曲轉角振型的虛部與實部。在給定邊界條件與參數范圍內，樁頂直徑相同時，由圖5(a)、圖6(a)來看：錐形樁第1階位移與轉角幅值明顯大于等截面樁，最大位移幅值位于樁頂，最大轉角幅值向樁底偏離；第2、第3階相差并不大，且最大位移幅值不在樁頂處。由圖5(b)、圖6(b)可知：錐形樁第1、第3階衰減幅值明顯低于等截面樁，第2階衰減幅值則高于等截面樁，這表明在欠阻尼狀態下地基阻尼對錐形樁基頻響應的影響較大，而對高頻響應的影響并不突出。

圖5 P-C邊界，樁的前3階截面橫向位移振型(r=1.736×10-3, s=5.417×10-3, p=2.207×10-4, β=3.744×10-4, k=0.034 3, c=g=0.02; n1=-m, n2=n3=n4=m)

圖6 P-C邊界，樁前3階截面彎曲轉角振型(r=1.736×10-3, s=5.417×10-3, p=2.207×10-4, β=3.744×10-4, k=0.034 3, c=g=0.02; n1=-m, n2=n3=n4=m)

圖7反映了P-C邊界樁頂直徑相同時，不同錐度系數m下樁的無量綱基頻ω1及其衰減系數δ1隨無量綱地基阻尼系數c的變化曲線。由圖7(a)可知：在欠阻尼狀態，m=0，0.1，0.3，0.5時對應的無量綱基頻ω1均隨無量綱地基阻尼系數c的增大而非線性降低，直至c=ccr達到各自臨界阻尼狀態時ω1剛好為0，之后隨著c繼續增大，樁進入過阻尼狀態，此時ω1≡0，樁不發生振動而變為純衰減運動，最后停止運動[27]；取相同的c值，錐度系數m值越大，欠阻尼狀態下基頻越小，進而衰減振動周期越長；m=0，0.1，0.3，0.5達到各自臨界阻尼狀態對應的無量綱臨界阻尼分別為ccr=0.074 15，0.068 14，0.057 16，0.047 52。由圖7(b)可見：在cccr時為過阻尼范圍，ω1≡0，特征方程有2個不相等的負實數根，此時變為純衰減運動，曲線開口向右，且開口隨m值的增大而減小，同時注意到不同m值曲線部分疏離明顯，表明過阻尼狀態下，錐角大小對樁的位移輸出響應有較大影響。

圖7 P-C邊界，不同錐度系數下樁無量綱基頻及對應衰減系數隨地基阻尼系數的變化關系曲線(r=1.736×10-3, s=5.417×10-3, p=2.207×10-4, β=3.744×10-4, k=0.034 3, g=0.02; n1=-m, n2= n3= n4= m)

此外，圖8描述了P-C邊界m=0.5且c∈[0, 0.03]的欠阻尼狀態下，不同比例系數n3時樁的無量綱基頻ω1隨c值的變化曲線，n3>0表示樁周土的橫向阻尼系數自樁頂至樁底逐漸線性減小，n3=0表示不變，n3<0表示線性增大。由圖8可知：c值較大時，樁周土地基阻尼系數沿樁身的變化對其基頻的影響不可忽略，需考慮由樁徑線性減小引起樁周土阻尼作用的變化。

圖8 P-C邊界，不同比例系數n3下樁無量綱基頻隨地基阻尼系數的變化關系曲線(r=1.736×10-3, s=5.417×10-3, p=2.207×10-4, β=3.744×10-4, k=0.034 3, g=0.02; m=0.5, n1=-m, n2=n4=m)

3.2.2 地基橫向彈性系數與剪切系數對基頻的影響

圖9、10分別反映了P-C邊界m=0.5及不同比例系數n2與n4時，欠阻尼狀態下樁周土無量綱地基橫向彈性系數k與剪切系數g對樁的無量綱基頻ω1的影響關系曲線，n2及n4>0表示樁周土的橫向彈性剛度與剪切剛度自樁頂至樁底逐漸線性減小，n2及n4=0表示不變，n2及n4<0表示線性增大。由圖9、圖10來看：欠阻尼自振基頻ω1均隨著k值與g值的增加而增大，進而衰減振動的周期隨k值與g值的增加反而減小；考慮k值或g值自樁頂至樁底逐漸線性增大時(n2或n4<0)，基頻ω1值高于均勻分布(n2或n4=0)；考慮k值或g值自樁頂至樁底逐漸線性減小時(n2或n4>0)，基頻ω1值低于均勻分布。此外，數值結果表明樁周土無量綱地基橫向彈性系數k與剪切系數g對其衰減系數幾無影響。

圖9 P-C邊界，不同比例系數n2下樁無量綱基頻隨地基橫向彈性系數的變化關系曲線(r=1.736×10-3, s=5.417×10-3, p=2.207×10-4, β=3.744×10-4, c=g=0.02; m=0.5, n1=-m, n3= n4= m)

圖10 P-C邊界條件，不同比例系數n4下無量綱基頻隨地基剪切系數的變化關系曲線(r=1.736×10-3, s=5.417×10-3, p=2.207×10-4, β=3.744×10-4, k=0.034 3, c=0.02; m=0.5, n1=-m, n2=n3=m)

3.2.3 樁-土界面摩擦力、軸向荷載與樁長徑比對基頻的影響

圖11描述了P-C邊界m=0.5及不同比例系數n1時，欠阻尼狀態下樁的無量綱基頻ω1隨無量綱樁側摩阻力β值的變化曲線，n1=0表示樁側摩阻力自樁頂至樁底不變，n1<0表示線性增大。由圖11可見：樁的基頻隨樁周土摩阻力的增加而增大，且-n1值越大，基頻的增幅越大；β值很小時影響并不明顯，但β值較大時不考慮樁-土界面摩擦力的影響會低估樁的固有頻率。此外，數值結果表明樁-土界面摩擦力對其衰減系數幾無影響。

圖11 P-C邊界，不同比例系數n1下樁無量綱基頻隨樁側摩阻力的變化關系曲線(r=1.736×10-3, s=5.417×10-3, p=2.207×10-4, k=0.034 3, c=g=0.02; m=0.5, n2=n3=n4=m)

圖12刻畫了P-C邊界樁頂直徑相同時，欠阻尼狀態下不同錐度系數m對應的樁無量綱基頻ω1隨樁頂無量綱軸向荷載p的變化曲線。由圖12來看：ω1隨p值的增加而快速減小，且減幅隨m值的增加而增大，當ω1減小至0時樁發生屈曲，此時軸向荷載為其屈曲臨界荷載pcr；m=0，0.1，0.3，0.5時對應的無量綱屈曲臨界荷載分別為pcr=0.075 8，0.065 4，0.047 2，0.032 0，即錐度系數越大，對應錐形樁的屈曲臨界荷載越小。這表明隨著樁身沿縱向逐漸變柔使其整體剛度降低，故而樁的屈曲穩定性顯著降低。此外，數值結果表明樁頂軸向荷載對其衰減系數并無影響。

圖12 P-C邊界，不同錐度系數下樁無量綱基頻隨軸向荷載的變化關系曲線(r=1.736×10-3, s=5.417×10-3, β=3.744×10-4, k=0.034 3, c=g=0.02; n1=-m, n2=n3=n4= m)

設錐形樁的樁長與樁頂直徑的比值為其長徑比即μ=l/d0，以樁頂直徑不變為前提，可通過調整樁長反映長徑比的變化。可知，當m值一定且不為零時，隨著樁長增大，錐角逐漸減小；相關無量綱參數中r、s隨樁長的增加而減小，k、β值隨樁長的增加而增大，c、g、p保持不變。為便于比較，將無量綱固有頻率ω轉化為含量綱的固有角頻率，并用λI表示。可得

(38)

圖13刻畫了P-C邊界樁頂直徑相同時，欠阻尼狀態下不同錐度系數m對應的樁基頻λI1隨樁長徑比μ的變化曲線。由圖13可知：樁的自振基頻隨樁長徑比的增加先快速降低后緩慢降低，進而趨于穩定；當μ<10時錐度系數與長徑比的耦合作用對基頻影響較大，當10<μ<20時該耦合作用對其基頻的影響逐漸減小，當μ>20時該耦合作用對其基頻的影響可以忽略不計。這表明隨著樁長徑比的增大，一方面樁身截面剪切變形與轉動慣量的影響逐漸降低即由Timoshenko梁逐漸向Euler-Bernoulli梁逼近；另一方面樁身錐角也逐漸減小，使得錐形樁的基頻逐漸趨向于等截面樁。此外，數值結果表明樁長徑比μ增加使基頻λI1對應衰減系數λR1有微小增長，可忽略不計，在此不再贅述。

圖13 P-C邊界，不同錐度系數下樁基頻隨其長徑比的變化關系曲線(p=2.207×10-4, c=g=0.02; n1=-m, n2=n3=n4=m)

4 結 論

基于Timoshenko梁理論，利用樁身微元體變形后的受力平衡條件建立了三參數Pasternak黏彈性地基中錐形樁的動力學模型，通過2個數值算例驗證了目前方法的適用性。進一步，應用微分求積法分析了圓截面錐形樁的橫向自由振動特性。以錐度系數衡量樁身錐角的變化，同時考慮軸向荷載、樁-土截面摩擦力及其沿樁身線性分布、樁長徑比、地基參數及其沿樁身分布情況等對樁固有特性的影響，重點探討了P-C邊界條件下樁的自振基頻及其衰減系數隨錐角與地基阻尼的變化規律。在給定參數范圍內，得到主要結論如下：

(1) 樁頂約束轉角時，固有頻率隨樁底約束的減弱明顯降低，而衰減系數小幅增大；相同參數時，各階固有頻率相差較大，而衰減系數相差微小，反映樁-土體系可近似視為比例阻尼系統。

(2) 當錐度系數m≤0.5時，樁的固有頻率及其衰減系數隨錐角的增加而降低，且受邊界條件影響較大。隨著地基阻尼的逐漸增大，錐形樁經歷欠阻尼、臨界阻尼和過阻尼狀態，且錐角越大，臨界阻尼越小。表明錐角與地基阻尼的有明顯的耦合效應。

(3) 樁周土的地基橫向彈性剛度、剪切剛度與地基阻尼較大時，對于錐形樁需考慮由樁徑變化引起樁-土相互作用沿樁身縱向分布的不均勻性。

(4) 樁的基頻隨樁側摩阻力的增加而增大，樁側摩阻力較大時不考慮樁-土界面摩擦力的影響會低估樁的固有頻率。

(5) 樁長與樁頂直徑一定時，隨著錐角的增大，樁身沿縱向逐漸變柔使其整體剛度降低，樁的屈曲臨界荷載明顯減小；樁頂直徑一定時，樁的自振基頻隨樁長的增加先快速降低后緩慢降低，進而趨于穩定。