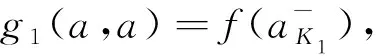單位區間上由G?del模和Galois聯絡生成的三角模

孫 杰, 張德學

(四川大學 數學學院, 四川 成都 610064)

三角模在模糊邏輯[1-2]、函數方程[3]等領域中有很重要的作用,它的結構與構造方法得到了廣泛的研究,系統的總結和論述參見文獻[3-4].利用Galois聯絡構造三角模是一種很有效的方法,例如連續的阿基米德模就是由單位區間上的乘積模和一類特殊的Galois聯絡生成的三角模.具體地說,二元運算T:[0,1]2→[0,1]是連續的阿基米德模當且僅當存在嚴格遞增的連續函數g:[0,1]→[0,1]使得g(1)=1并且

T(x,y)=g(-1)(g(x)·g(y)),

其中g(-1)是g的偽逆,即

g(-1)(x)=min{y|x≤g(y)}=

詳見文獻[3]的定理2.2.1.注意到此時偽逆g(-1)就是g的左伴,文獻[5]指出可以利用Galois聯絡構造偏序集上的三角模(定義見文獻[6]或定義1.4),并證明了以下結論.

定理 1.1設P、Q是有最大元和最小元的偏序集,d:P→Q和g:Q→P是保序映射并且d是g的左伴.若T是P上的三角模且對任意x,y∈Q恒有

T(g(x),g(y))∈g(Q)∪{ω∈P|ω≤g(0)},

則Tg是Q上的三角模,其中

設P=Q=[0,1],d┤g:[0,1]→[0,1]是Galois聯絡,T是[0,1]上的G?del模(也稱取小模),即T(x,y)=min{x,y}.則條件

T(g(x),g(y))∈g(Q)∪{ω∈P|ω≤g(0)}

恒成立,于是由定理1.1得

Tg(x,y)=

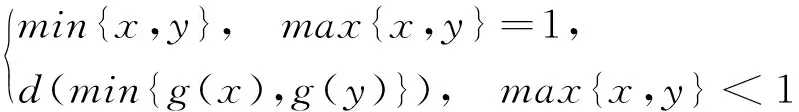
是[0,1]上的三角模,稱為由G?del模和Galois聯絡d┤g生成的三角模.本文研究了這類三角模的結構,給出了完整的刻畫,證明了兩個這樣的三角模同構當且僅當彼此的冪等元集之間存在保序同胚.

1 預備知識

這一節簡要回顧本文將用到的Galois聯絡的基本性質以及偏序集上三角模的定義.單位區間上(連續、左連續)三角模的概念和基本性質請參考文獻[3-4].

定義 1.1[7]設P和Q是偏序集,d:P→Q和g:Q→P是保序映射.若對任意p∈P,q∈Q都有d(p)≤q?p≤g(q),則稱d是g的左伴,g是d的右伴.此時稱(d,g)為一對Galois聯絡,記作d┤g:Q→P或d┤g.

定理 1.2[7]設d:P→Q和g:Q→P是偏序集之間的保序映射,則下列條件等價:

1)d┤g;

2)dg≤1Q且1P≤gd;

3) ?x∈P,d(x)=min{y∈Q|x≤g(y)};

4) ?x∈Q,g(y)=max{x∈P|d(x)≤y}.

定理 1.3[7]設g:P→Q是保序映射并且P是完備格.則g保下確界當且僅當g有左伴.特別的,保序映射g:[0,1]→[0,1]有左伴等價于g右連續且g(1)=1.

定義 1.4[6]設P是有最大元1的偏序集.稱二元運算T:P×P→P是P上的三角模若T在每個分量上保序且滿足下列條件:

(T1)T(x,y)=T(y,x);

(T2)T(1,x)=T(x,1)=x;

(T3)T(T(x,y),z)=T(x,T(y,z)).

若T是偏序集P上的三角模,則(P,T)是以1為單位元的幺半群.設T是偏序集P上的三角模,S是偏序集Q上的三角模.稱T與S同構若存在序同構f:P→Q使得任給x,y∈P,f°T(x,y)=S(f(x),f(y)).

2 主要結論

除非另外聲明,總是假設d┤g:[0,1]→[0,1]是Galois聯絡,Tg表示由G?del模和d┤g生成的三角模,即

Tg(x,y)=

稱單位區間[0,1]的子集K關于上確界封閉若任給A?K恒有∨A∈K.特別的,0=∨?∈K.

引理 2.1設K?[0,1]關于上確界封閉.任給x∈[0,1],令

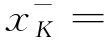
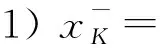
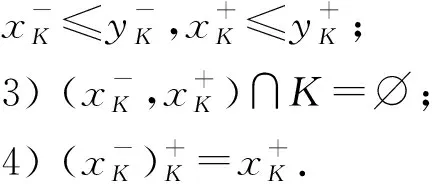
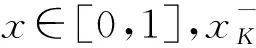
定理 2.2設K是Tg的冪等元集,即K={x∈[0,1]|Tg(x,x)=x}.則:

1)K={dg(x)|x∈[0,1]}∪{1};

3) 任給x,y∈[0,1),Tg(x,y)=min

證明1) 由Tg的定義,

于是

K={x∈[0,1]|Tg(x,x)=x}=

{x∈[0,1]|dg(x)=x}∪{1}.

(1)

又因為任給x∈[0,1],dgdg(x)=dg(x),所以K={dg(x)|x∈[0,1]}∪{1}.

2) 為了說明K關于上確界封閉只需證明任給A?K{1},supA∈K.若A=?則supA=0∈K;若A≠?,則由(1)式知對任意的x∈A都有x=dg(x),于是A=dg(A).因為

supA=supdg(A)≤dg(supA)≤supA,

3) 由Tg的定義和2)直接可得.

推論 2.3設K是Tg的冪等元之集.則下列各條等價:

1)Tg=min;

2)Tg連續;

3)Tg左連續;

4)K=[0,1].

證明只需證明3)?4)?1).

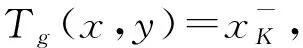
從而K=[0,1].

4)?1) 任給x,y<1,由定理2.2的3)可得

于是Tg=min.

由定理2.2知由G?del模和Galois聯絡生成的三角模的冪等元集包含1且關于上確界封閉,下面的定理表明反過來結論也成立.

定理 2.4設K是單位區間[0,1]關于上確界封閉的子集并且包含1,則存在Galois聯絡d┤g:[0,1]→[0,1]使得K是三角模Tg的冪等元集.

由引理2.1的4)可得任給x∈[0,1],g(x)=g(x-).下面說明g有左伴,設為d:[0,1]→[0,1],并且Galois聯絡d┤g滿足條件.

第一步g單調遞增.說明g在K上的限制嚴格遞增.設x,y∈K且x

第二步g右連續,于是有左伴.任給0≤x<1,分2種情形討論.

情形 1x=x+.由g的定義易知此時g(x)=x.由x+的定義知存在K中嚴格遞減的序列{an}n收斂于x.因為對任意n≥1都有

所以{g(an)}n收斂于x(=g(x)).利用g的單調性以及limg(an)=g(x)可得g在x處右連續.

情形 2x

第三步K是Tg的冪等元之集,即K={dg(x)|x∈[0,1]}∪{1},其中d是g的左伴.由于K={x-|x∈[0,1]},說明任給x∈[0,1],dg(x)=x-即可.

由定理1.2的3),dg(x)=min{t∈[0,1]|g(t)≥g(x)}.一方面,由g(x-)=g(x)可得dg(x)≤x-.另一方面,任給y

定理2.2的3)表明由G?del模和Galois聯絡生成的三角模可由它的冪等元集確定,因此這樣的三角模可以通過它們的冪等元集來分類,這就是下面的結論.

定理 2.5設di┤gi:[0,1]→[0,1]是Galois聯絡,Ki是三角模Tgi的冪等元之集,i=1,2.則下列各條等價:

1) 三角模Tg1與Tg2同構,這等價于存在保序的雙射h:[0,1]→[0,1]使得h°Tg1=Tg2°(h×h);

2) 幺半群([0,1],Tg1)與幺半群([0,1],Tg2)同構;

3) 存在K1到K2的保序同胚.

證明1)?2) 顯然.

2)?3) 設f:([0,1],Tg1)→([0,1],Tg2)是幺半群同構.下面說明f在K1上的限制是K1到K2的保序的同胚.

首先,由于f:([0,1],Tg1)→([0,1],Tg2)是幺半群同構,K1和K2分別是兩個幺半群的冪等元之集,故f在K1上的限制f|K1是K1到K2的雙射.

其次說明f|K1:K1→K2保序.若不然,則存在x,y∈K1滿足xf(y),于是

Tg2(f(x),f(y))≤f(y)

與f同構矛盾.

同理可知f|K1的逆映射也連續,于是f|K1:K1→K2是保序同胚映射.

h(x)=