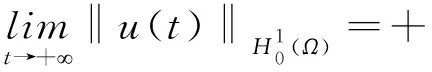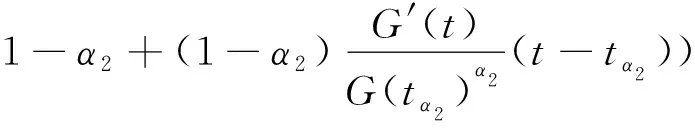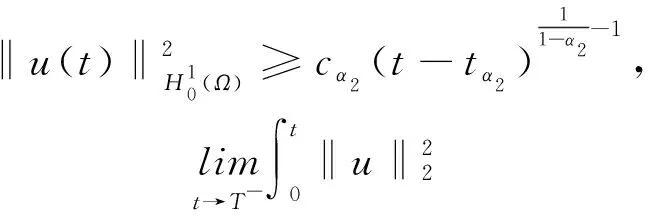一類半線性偽拋物方程的初邊值問題
高雪妍, 鄭雅勻, 楊 晗
(西南交通大學 數學學院, 四川 成都 611756)
0 引言
研究半線性偽拋物方程的初邊值問題
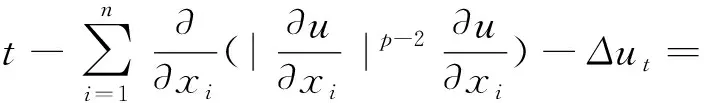
φ(u),Ω×(0,T),
(1)
u(x,t)=0, ?Ω×(0,T),
(2)
u(x,t)=u0(x),Ω,
(3)
其中
這里Ω?n是一個邊界充分光滑的有界區域,p≥2.上述方程組可用來描述非線性、色散、長波的單向傳播[1-2]和種群的聚集[3]等多種現象,也可用于分析有緣半導體中的非平穩過程[4-5].Δut-ut對應自由電子密度率,ut對應自由電荷電流的線性耗散,φ(u)描述自由電子電流的來源.
現回顧與問題(1)~(3)有關的文獻的一些經典結論.當(1)式中Δut項缺失時,Tsutsumi[6]研究了退化拋物型方程
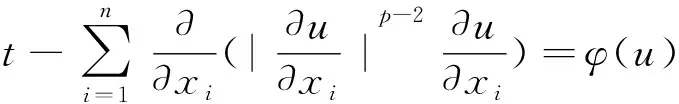
的初邊值問題.用Galerkin方法、單調算子理論和緊致性定理研究了方程的整體弱解的存在性與爆破方面的結論.當(1)式Δut項變成u時,Liu等[7]考慮了半線性熱方程
ut-Δu+u=|u|p-1u
(4)
的柯西問題.在初值屬于穩定性集時,研究了方程(4)弱解的整體存在性和指數衰減估計,在初值屬于不穩定性集時,研究了弱解在有限時刻爆破.Xu等[8]等研究了半線性偽拋物方程
ut-Δu-Δut=u1+α
(5)
的初邊值問題.在初始值滿足適當的條件下,通過引入穩定性集與不穩定性集得到弱解的整體存在性、漸近性和不存在性,并通過比較原理得到具有初始能量為正時解在有限時刻爆破.Chen等[9]研究了具有對數非線性項的半線性偽拋物方程
ut-Δu-Δut=ulog|u|,
通過使用對數Sobolev不等式和一族勢井,得到方程整體弱解存在性、解的漸近性質和在正無窮處的指數增長性.另一方面,還討論了解的真空隔離.
本文研究(5)式的退化情形,即(1)式,考慮初值在何種條件下弱解的整體存在及在何種條件下解爆破,并且研究解存在真空隔離現象.
1 準備工作
為了后面的應用,先給出幾個引理,引理1.1和1.2的證明詳見文獻[6].
令
I(u)=a(u)-b(u),
(6)
其中
下面是與勢井理論相關的基本結論.
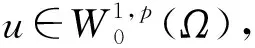
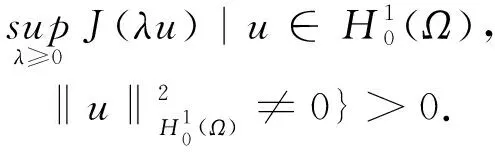
(7)
引入集合
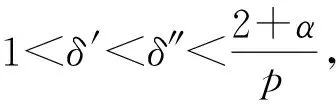
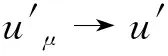
W={u|u∈W1,p0(Ω),0≤J(λu) λ∈[0,1]}. 事實上,可證得對任意t,u0(x)∈W時,u(x)∈W(見定理3.1).因此,稱該集合為穩定性集. 引理 1.2 W=W*∪{0}, 其中 W*={u|u∈W1,p0(Ω),a(u)-b(u)>0, J(u) 令 N={u∈W1,p0(Ω)|I(u)=0,‖u‖p1,p(Ω)≠0}, W={u∈W1,p0(Ω)|I(u)>0, J(u) V={u∈W1,p0(Ω)|I(u)<0,J(u) 下面引入一勢井族.對δ>0,定義 Iδ(u)=δa(u)-b(u), Nδ={u∈W1,p0(Ω)|Iδ(u)>0, J(u) Wδ={u∈W1,p0(Ω)|Iδ(u)>0, J(u) Vδ={u∈W1,p0(Ω)|Iδ(u)<0,J(u) 下面給出勢井族的相關結論. 1) 若0<‖u‖1,p(Ω) 2) 若Iδ(u)<0,則‖u‖1,p(Ω)>r(δ).特別地,若I(u)<0,則‖u‖1,p(Ω)>r(1). 3) 若Iδ(u)=0,則‖u‖1,p(Ω)≥r(δ)或‖u‖1,p(Ω)=0,特別地,若I(u)=0,則‖u‖1,p(Ω)≥r(1),或‖u‖1,p(Ω)=0. 證明1)的證明.由0<‖u‖1,p(Ω) Iδ(u)=δ‖u‖p1,p(Ω)-‖u‖2+α2+α(Ω)≥ δ‖u‖p1,p(Ω)-C1+α*‖u‖2+α1,p(Ω)≥ ‖u‖p1,p(Ω)(δ-C1+α*‖u‖2+α-p1,p(Ω))>0, 由Iδ(u)的定義,1)得證. 2)的證明.由Iδ(u)<0,有 0>δ‖u‖p1,p(Ω)-‖u‖2+α2+α(Ω)≥ δ‖u‖p1,p(Ω)-C1+α*‖u‖2+α1,p(Ω)≥ ‖u‖p1,p(Ω)(δ-C1+α*‖u‖2+α-p1,p(Ω)), 得‖u‖1,p(Ω)>r(δ). 3)的證明.若Iδ(u)=0,且‖u‖1,p(Ω)≠0,則有 δ‖u‖p1,p(Ω)-‖u‖2+α2+α(Ω)≥ δ‖u‖p1,p(Ω)-C1+α*‖u‖2+α1,p(Ω)= ‖u‖p1,p(Ω)(δ-C1+α*‖u‖2+α-p1,p(Ω))=0, 得‖u‖1,p(Ω)≥r(δ). 4)的證明.由引理1.3的3)和 下面給出d(δ)的相關結論. 引理 1.42+α>p,p>2,d(δ)滿足下列性質: 證明1)u∈N,則由引理1.3的3)可得‖u‖1,p(Ω)≥r(δ),從而由 c(δ)rp(δ)≥c(δ)r2(δ), 得到d(δ)≥c(δ)r2(δ). 使得Iδ(λu)=0.從而λu∈Nδ,且 J(v) 事實上,由引理1.4的2)得 Iδ(λ(δ)u)=0,λ(δ″)=1. 令g(λ)=J(λu),得 (1-δ)λp-1‖u‖p1,p(Ω), J(v)-J(u)=g(1)-g(λ(δ′))≥ (1-δ″)λp-1(δ′)rp(δ″)(λ(δ″)-λ(δ′))= ε(δ′,δ″)>0. J(u)-J(v)≥ (δ″-1)λp-1(δ″)rp(δ″)(λ(δ′)-λ(δ″))= ε(δ′,δ″)>0. 現定義 由引理1.4,d0≥0. 下面研究Iδ(u)的不變號性. 弱解的整體存在性需要分情況來討論.本節先討論p>2+α時的情形,下節再討論p<2+α時的情形. u∈L∞([0,T];W1,p0(Ω)), (8) ut∈L2([0,T];L2(Ω)). (9) 若n 若在Ω內幾乎處處有u0(x)≥0,則對任一固定的t≥0,u(x,t)≥0在Ω內幾乎處處成立,并且此時u(x,t)是問題(1)~(3)的解. 證明令 m=1,2,…,n (10) 滿足 (φ(um(t)),ωj), 1≤j≤m, (11) (12) 在W1,p0(Ω)內,其中 (13) 由Sobolev嵌入定理及Young不等式得 由此可得 由這兩個估計及Aubin緊性引理知,存在函數u及{um}的子序列{uμ},使得 uμ(T)→u(T)于W1,p0(Ω)弱收斂, uμ→u于L2+α([0,T];L2+α(Ω))弱收斂, Auμ→Au于L([0,T];W-1,p(p-1)(Ω))弱*收斂.(14) 這就說明u是問題(1)~(3)的解. 下面證明問題(1)~(3)的弱解是唯一的.事實上,設u1與u2是問題(1)~(3)的兩個解.記ω=u1-u2,則ω滿足 其中 在方程(11)兩端對ω作內積,并利用A的單調性與Sobolev嵌入定理,可得 下面證明解的保號性,即當u0≥0時,u≥0.記 V([0,T];W1,p0(Ω))={v(t)∈L2([0,T]; W1,p0(Ω)),v′(t)∈L2(Ω)}, 用任意C1類函數f(t)乘(11)式并在[0,t]上積分,得 取m=μ(即以{um}中的收斂子列代替{um}),固定j,并令μ→∞取極限得 這說明 ?ψ∈V([0,T];W1,p0(Ω)). (16) 特別地,取ψ(s)=v(s)-u(s),其中v(s)=sup{u(s),0},則有 由v(s)的定義和(16)式可得 (Av-Au,v-u)≥0. 故 (17) 從而,若u0(x)≥0在Ω內幾乎處處成立,則(17)式右邊恒為0,左端幾乎處處為0,v(t)又是u(t)的正部.可得:當t≥0時,有u(x,t)≥0在Ω內幾乎處處成立. u∈L∞([0,T];W1,p0(Ω)), ut∈L2([0,T];L2(Ω)), 及 ‖u(t)‖L2(Ω)≤‖u(s)‖L2(Ω), t≥s≥0. (18) 若幾乎處處在Ω內有u0(x)≥0,則對任意固定的t>0,u(x,t)≥0幾乎處處在Ω內成立.從而u(x,t)≥0是問題(1)~(3)的解. 證明再一次使用Galerkin方法.{ωi}及um的意義見定理2.1的證明.設 {u0m}?W, (19) 在W1,p0(Ω)內,由常微分方程的存在性定理知,存在tm>0,使得在[0,tm]內(11)式有解um(t),并且(13)式成立,即 J(um)≤J(u0m),t∈[0,tm]. (20) 證明 um(t)∈W, ?t≥0. (21) 假設(21)式不成立,以t*表示使um(t*)?W的最小的時間.由連續性知um(t*)∈?W,故由引理1.4得 J(um(t*))=d, (22) 或 a(um(t*))-b(um(t*))=0. (23) 若(22)式成立,這與(20)式及u0m∈W相矛盾.若(23)式成立,則 也得到同樣的矛盾,說明(21)式成立. 從(20)式及引理1.2得 J(u0m(t))≤C. 由此得 ‖um‖L∞([0,T];W1,p0(Ω))≤C, 利用Aubin緊性定理及單調算子理論可知,存在函數u及{um}的子序列{uμ}使(14)式成立,故u是(1)~(3)的解. a(u(t))-b(u(t))≥0. (24) 另一方面,在(16)式中取ψ(s)=u(s),不難得到 (25) 由(24)及(25)式立得(16)式. 本定理的其他結論與定理2.1的一些證明過程類似可得. 先建立問題(1)~(3)的解的不變集合. Iδ(u0)=(δ-1)‖u‖p1,p(Ω)+I(u0)>0, 將(1)式乘以ut,并在Ω×[0,t)上分別積分, (26) Iδ(u(t0))=0, ‖u(t0)‖1,p(Ω)≠0, 或J(u0)=d(δ). 由命題4.1,J(u0) 2)J(u0)=d(δ),I(u0)<0時,令u=u(x,t)是(1)~(3)的弱解,T是u的最大存在時間. 如果不成立,則存在t0∈(0,T),使得當0≤t u(x,t)∈Vδ,u(x,t0)∈V. 因此,存在 由(26)式,J(u(t0))=d(δ)不成立. 若0 ‖u‖1,p(Ω)≥r(δ), 0 由d(δ)的定義,得J(u(t0))≥d(δ),這也與(26)式矛盾. 1) 當I(u0)>0時,對任意δ1<δ<δ2,有u∈Wδ; 2) 當I(u0)<0時,對任意δ1<δ<δ2,有u∈Vδ. 證明1) 因為I(u0)>0,且Iδ(u)的符號在δ1<δ<δ2上不變,則有 Iδ(u0)>0,δ∈(δ1,δ2). 另一方面,由引理1.4和能量公式 J(u0)=d(δ1)= d(δ2) (27) 已知J(u0) 2) 由引理1.5和I(u0)<0,得 Iδ(u0)<0,δ∈(δ1,δ2). 另一方面,能量公式(27)和 0 表明J(u0) u∈Vδ,δ1<δ<δ2. 余下的證明與命題4.1的2)中的證明類似. 推論 4.2若將推論4.1中的假設J(u0)=σ換成0 結果是,若0 推論4.1和推論4.2的結果表明,0 Uσ={u∈W1,p0(Ω)|‖u‖p1,p(Ω)≠0, Iδ(u0)=0,δ1<δ<δ2}, 使得問題(1)~(3)在Uσ內只有零解. 隨著σ的減小,真空區Uσ變得越來越大,即若σ1<σ2,Uσ2 注 4.2如下圖,在整個區域W內方程有解,在Uσ區域內只有零解,把這個現象稱為真空隔離現象. 為了處理其他情況,有下面的命題. 1)I(u0)>0時,對所有0≤t 2)I(u0)<0時,對所有0≤t 其中T是u(x,t)的最大存在時間. 證明 1) 若結論不成立,則存在t1∈(0,T),使得對所有0 I(u(t1))=0,I(u(t))>0. 然后結合 I(u)=-(u′,u)-(?u′,?u)≠0, 對所有0 (28) 對所有0 2) 若結論不成立,則存在t1∈(0,T),使得對所有0 I(u(t1))=0,I(u(t))>0. 類似1)的證明,對所有0 J(u)=J(u0)- (29) 同樣,由引理1.3和0≤t 現在來討論問題(1)~(3)的解的爆破.首先給出解在+∞處爆破的定義. 定義 5.1(在+∞處的爆破) 設u(x,t)是問題(1)~(3)的弱解,若解的最大存在時間T=+∞,且 則u(x,t)在+∞處爆破. 證明因為使用常用的凸算子方法和反證法未得到方程組的弱解在有限處有關爆破的相關結論,所以本章暫研究問題(1)~(3)的解在+∞處產生爆破的問題. 令 則當t>0時,有 G″(t)=-2I(u(t))>0. 事實上,由J(u)、I(u)定義得 J(u)= (30) 因為I(u)<0,所以由Sobolev嵌入定理得 (31) 利用(28)、(30)和(31)式得 G″(t)=-2pJ(u)+ (32) 因此,對所有t≥0,有 (33) 表明u(x,t)在+∞處爆破.因為 利用(32)和(33)式,得 G(t)G″(t)-(G′(t))2=[-2p(J(u0)- 上面的不等式可以由H?lder不等式推出,且 因此,對任意0<α2<1,有 G(t)G″(t)-α2(G′(t))2≥ 由(33)式知,存在t1>0,使得 G(t)G″(t)-α2(G′(t))2>0,t≥t1, 則可得 (G(t)1-α2)′=(1-α2)G(t)-α2G′(t), (G(t)1-α2)″=(1-α2)G(t)-α2-1× [-α2(G′(t))2+G(t)G″(t)]≥0. 令tα2≥t1,且滿足G(tα2)>0,則 且 其中 由G″(t)>0,有 對任意0<α2<1,從而對所有t≥tα2,有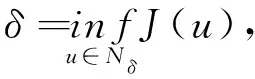

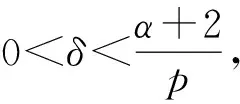
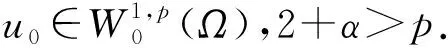
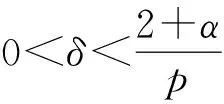
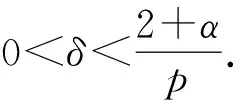
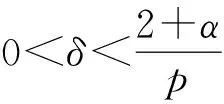
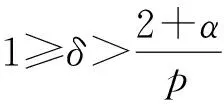
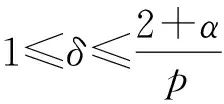
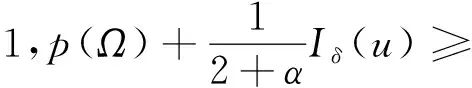
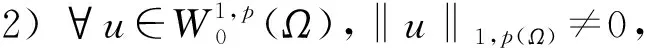
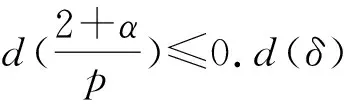
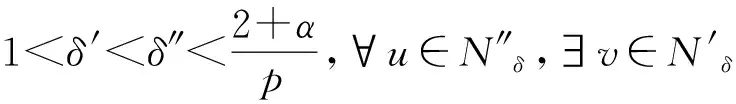
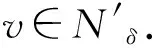
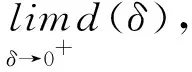
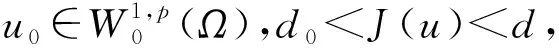
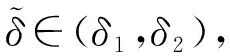
2 p>2+α時的整體存在性和唯一性
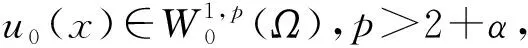
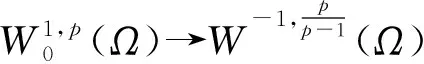
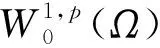
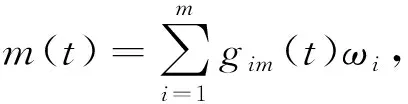
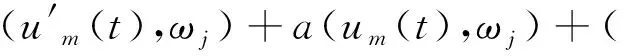
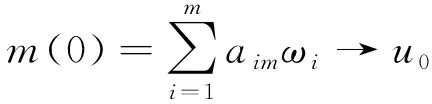
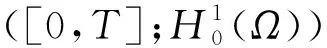
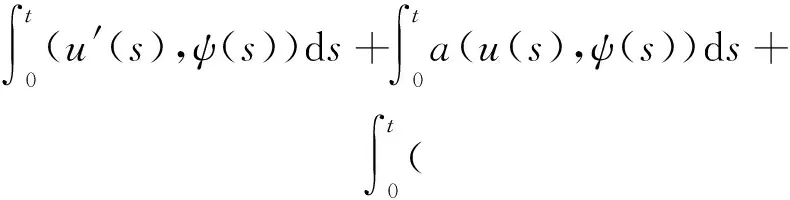
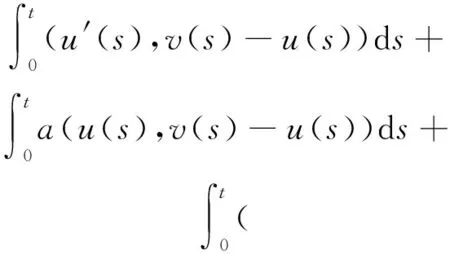
3 p<2+α時的整體存在性
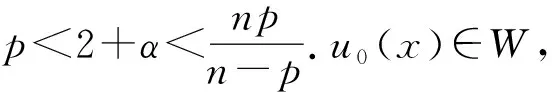
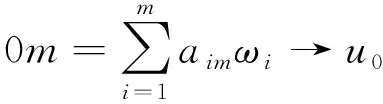
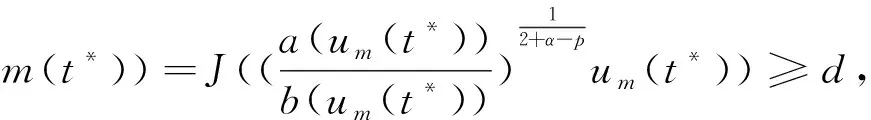
4 解的真空隔離
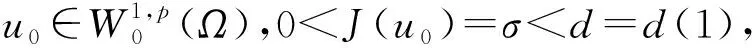
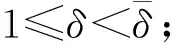
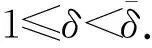
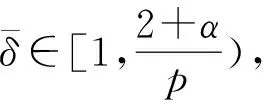
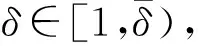
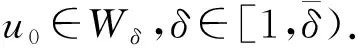
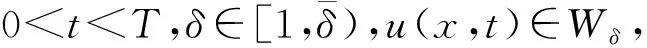
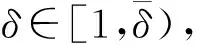
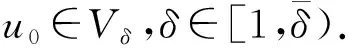
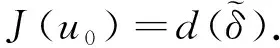
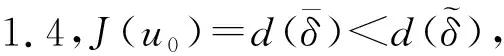
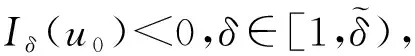
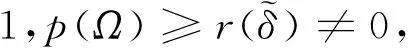
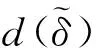
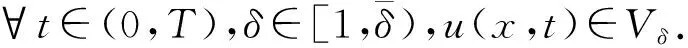
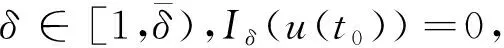
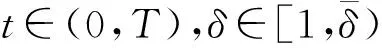
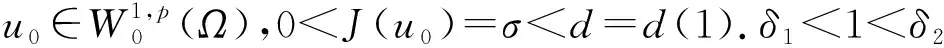


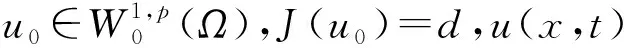
5 爆破現象