泛函積分方法與金屬氫星體模型中物態性質與溫度及磁場漲落研究
趙 豐, 顏 駿, 周良建, 詹 路, 黃 憶
(四川師范大學 物理與電子工程學院, 四川 成都 610066)
泛函積分方法來源于量子場論和粒子物理的研究,目前在物理學的各個領域都有廣泛的應用.泛函積分是一種非常靈活的數學工具,也是現代理論物理中最強有力的方法之一[1-4],這類方法特別適用于計算統計物理中的集體激發譜,如庫侖相互作用粒子系統中的等離子體振蕩,有限溫度下的玻色凝聚,超流和超導理論中的量子渦旋和長波聲子,極化子的自能等問題.泛函積分方法還可以使相變、激光、Kondo效應、伊辛模型等理論中的復雜問題變得相對簡單.俄羅斯學者Popov[1-2]和德國學者Kleinert[4]曾對泛函積分方法進行過比較系統的研究并做出了重要貢獻.
近年來,四川師范大學課題組將泛函積分方法應用于物理學的各個領域,取得了一系列的研究成果.在統計物理和凝聚態物理方面,有原子光學中的Dicke模型[5],高溫超導中的Boson-Fermion模型[6-7],費米凝聚中的sine-Gordon-Thirring模型[8-12],反鐵磁體中的三帶Hubbard模型[13-14],主要研究了上述模型中的激發譜、自由能、費米子凝聚譜等物理性質,還計算了隨機散射通道模型中傳遞函數的概率分布函數[15].在引力物理和相對論天體物理方面,根據泛函積分方法研究了非對易時空中費米物質的集體激發譜[16],導出了點物質黑洞背景下物質的量子漲落和關聯函數[17-19],計算了暗能量混合的費米孤子星的質量和物態參量[20].在研究這些物理問題的過程中,形成了一種新的變分泛函積分方法,這一方法可以有效地研究模型在強耦合區間的的物理性質.
金屬氫是超高壓環境中形成的一種特殊物質,通常存在固態金屬氫和液態金屬氫2種物態.固態金屬氫中離子能保持晶格結構,具有一定導電性質,在更強的壓力下固態金屬氫中晶格結構被破壞并轉化為液態形式的金屬氫,所以在高壓環境下的金屬氫密度比普通氫的密度更大.在地球上不存在自然的金屬氫,人們只有在實驗室通過人工合成固態金屬氫,這是目前高壓凝聚態物理中具有挑戰性的研究課題.
木星是太陽系中存在的一種重型的巨行星,在巨大壓力下其內部可能形成液態形式的金屬氫,在木星較快的自轉作用下金屬氫中的電子將形成較強的電流,從而對木星的磁場的形成和強度產生重要的影響.瑞士天體物理學家Mayor和Queloz[21]由于發現了系外巨行星獲得了2019年度諾貝爾物理獎,這些巨行星中也可能存在不同形式的金屬氫物質[22],因此,研究金屬氫對理解巨行星的各種天文學觀測性質就具有重要的物理意義.
本文將根據泛函積分方法研究金屬氫的物態關系,并進一步分析轉動巨行星中的流體力學性質,磁場強度漲落和溫度漲落等物理效應.
1 泛函積分與致密電子-離子系統的晶體結構
本節將在泛函積分方法框架下探討晶體結構的微觀理論,該方法由Popov[1]于1981年提出,之后加以推廣[2].晶體理論的泛函積分方法還可用來研究稠密電子-離子系統的周期晶格,這一方法由Anisimov等[23]于1986年提出.一個具有庫倫相互作用的電子和離子組成的系統中,晶體的性質是由集體激發聲子決定的,一個微觀理論必須描述聲子-電子和離子系統的相互作用,泛函積分方法可以完成這項工作.主要操作思想是將電子和離子的原始作用量轉為用電勢場φ(x,τ)描述的有效泛函作用量,再從有效泛函作用量的穩定條件找到定態場φ0(x),并考慮Seff穩定點附近的漲落效應.
金屬氫模型中電子和離子系統的泛函作用量為
其中
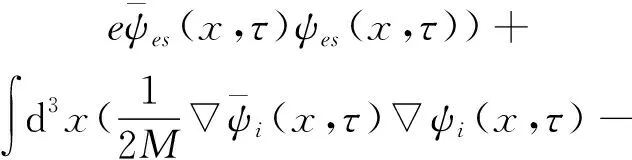
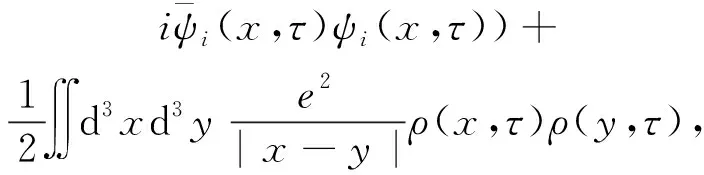
(2)
(3)
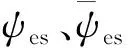
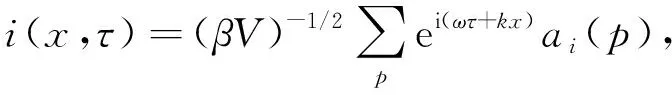
(4)
其中,p=(k,ω)是動量,松原頻率為ω=(2n+1)π/β,β-1=T是有限溫度,λi是化學勢.首先將庫侖相互作用轉換為電勢玻色場φ(x,τ)的作用,引入如下高斯積分:
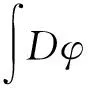
(5)
再對φ(x,τ)進行移位變換
(6)
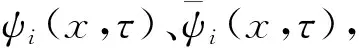
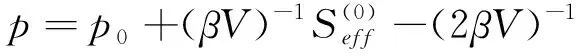
(7)
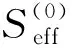
Seff[pl,α,ql,α,φ(x,τ)]=
2lndet[?τ+(2m)-12+λe+ieφ(x,τ)]/?τ+
(2m)-12+λe+
ieφ(ql,α(τ),τ)],
(8)
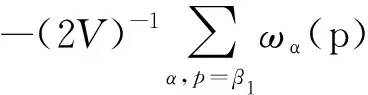
(9)
其中p0和ρ5/3成正比,(7)式中第3項可以展開為
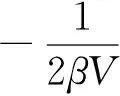
(10)
其中Π是格林函數的極化算子,所以有
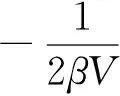
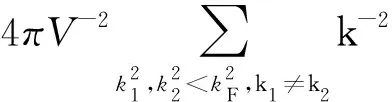
(11)
(12)
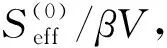
exp(-ηπn2+2πi(n,γ-δ))+
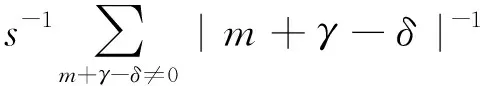
|m+γ-δ|)-ηs-2η-1/2},
(13)
其中
(14)
C1=2.837 297 479 482,
體心立方晶格(bcc)中
C2=2.888 461 503 050,
面心立方晶格(fcc)中
C3=2.888 282 119 020,
六角密堆晶格(hcp)中
C4=2.888 168 750 480,
(7)式最后1項修正項表示零點能,在大壓強下滿足
2 金屬氫中的晶體-液體轉化
利用金屬理論的泛函積分方法可證明,隨著壓強進一步增加,晶體系統可能變為液態,這時晶格的零點振動將被破壞.為了計算固態金屬氫轉化為液態金屬的臨界密度,應先計算液態金屬氫的壓強,然后再與第1節已計算的固態金屬氫的壓強進行比較,這一壓強前3項的表達式[23]為
(15)
參數M-1/2的存在確保了零點振動能帶來的影響,液態金屬氫的壓強[24]為
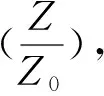
(16)
其中
(17)
是理想費米電子氣體和等離子氣體的混合壓強,Z是具有庫侖作用的電中性等離子體的配分函數.為了計算(βV)-1ln(Z/Z0),可采用如下等離子體作用量
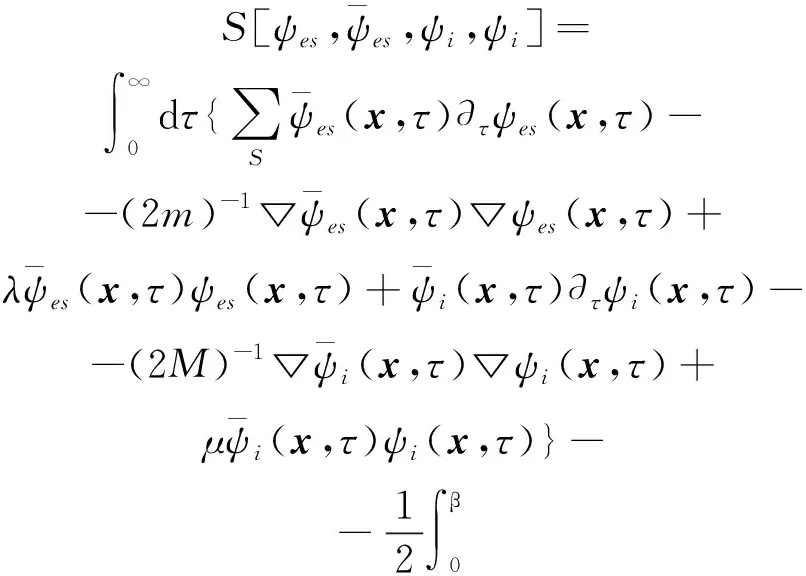
其中電荷密度ρ(x,τ)為
ρ(x,τ)=ρi(x,τ)-ρe(x,τ)=
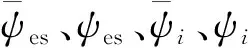
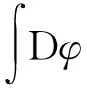
再進行下列移位變換后消去非局域庫侖項
最后得到如下作用量
ieφ(x,τ))ψes(x,τ)+
ieφ(x,τ))ψi(x,τ)}.
(22)
對電子、離子費米場進行泛函積分后得到的有效作用量為
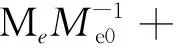
(23)
并引入記號
Me=?τ+(2m)-12+λ+ieφ(x,τ),
Me0=Me|φ=0;
Mi=?τ+(2m)-12+μ-ieφ(x,τ),
Mi0=Mi|φ=0.
(24)
考慮了電子自旋后lndet前會出現2,將(23)式中φ的冪展開到2階后得自由電子的格林函數Ges,以及離子的格林函數Gi,對φ場積分后得如下壓強的修正表達式
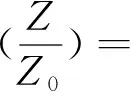
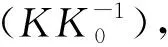
(25)
其中矩陣元K與電子和的離子的格林函數極化算符有關,這里極化算符表示電子和離子的自由電子的格林函數乘積之和.再將lndet展開并取低溫極限后壓強的修正表達式為
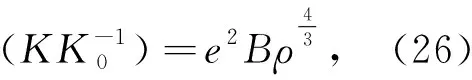
根據(17)和(26)式得如下液體金屬氫的物態關系
(27)
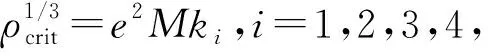
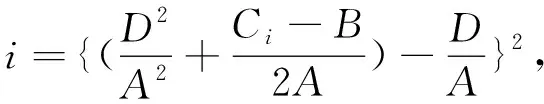
(28)
與不同類型晶格中常數Ci有關系,其余常數的數值分為
A=1.914 156 000,B=1.477 117 533,
D=1.534 990 062,
所以不同類型晶格的金屬氫轉化為液態金屬氫時的臨界粒子數密度有一定的差異.
3 轉動星體中的流體力學性質
轉動情況下的星體平衡方程[25-26]為
(29)
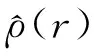
(30)
其中,
此時徑向微分方程(29)的解為
(31)
其中
N=(4πGβ2d2-2ω2d),
M=4πGβ2d2·(5/3ρc)>0.
所以積分常數應取C1=C2=0,根據(31)式可進一步導出粒子數密度的漲落比值為
(32)
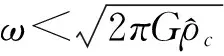
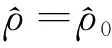
(33)
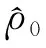
(34)
將(33)式代入方程(34)可導出如下修正形式的Lane-Emden方程
(35)
其中,ξ=Dr,U=Φ/k1,f=(ω/D)2×(1/3k1).文獻[29]采用變參數法討論了Lane-Emden方程的近似解,文獻[30-31]分析了木星中多方指數n=1,2時Lane-Emden方程密度的解析解,下面進一步研究2階非線性微分方程(35)的級數解.這時邊界條件設為:當ξ=0時,U=0,dU/dξ=0,確定星體半徑的條件為:當ξ=ξn時,U=0.將方程的解用級數展開為
U=a0+a1ξ+a2ξ2+
a3ξ3+a4ξ4+a5ξ5+a6ξ6,
(36)
根據邊界條件可以定出其中的系數分別為
(37)
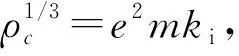
擾動時行星表面附近的流體元的運動方程[32]為
(38)
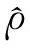
(39)
由此可以得到聲波在星體內部的傳播時間約為
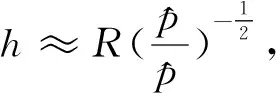
(40)
聲波的傳播速度約為
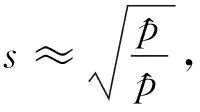
(41)
液態金屬氫的物態方程為
(42)
其中,
k1=α1/α,α=C/M,k2=α2/α4/5,
α1=(1/me+1/M)A,α2=e2B,
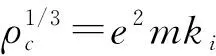
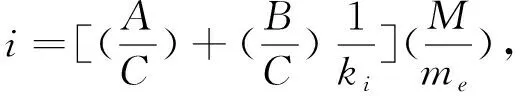
(43)
其中數值常數
A=1.914 156 000,B=1.477 117 533,
C=2.871 230 000.
根據(40)和(43)式可以計算出4種類型金屬氫星體中聲波傳播時間的比值約為
τ1∶τ2∶τ3∶τ4=
1.218 61∶1.218 60∶1.218 60∶1.218 60.(44)
所以不同類型的金屬氫星體的聲波傳播時間幾乎一致,如木星中sc晶格的聲波傳播時間約為1 958.355 0 s,bcc晶格,fcc晶格和hcp晶格的聲波傳播時間約為1 958.338 5 s,其中SC晶格和其余3種晶格的傳播時間只有微小差別.
4 星體中磁場和溫度的漲落關系
設星體內矢勢A滿足的方程為
2A=-μ0J,A=0,
(45)
其中J是流密度,那么方程的解為
(46)
其中x′是源點,x是場點,r為x′到x的距離,對解求旋度即可導出磁場感應強度的表達式,即
B=×A=
(48)
在具體計算中可設星體半徑為R,總電荷量為Q,則Q=(4πR3/3)ne,這里ne表示電荷的粒子數密度.在球坐標下J(x′)=neω×r′,ω是星體的轉動角速度.當r (49) (50) δB1∶δB2∶δB3∶δB4≈ 51 105.53∶50 955.75∶50 926.57∶50 908.22,(51) 這時,磁場強度的比值逐漸變小,文獻[31]給出的木星內部的磁場強度和角速度及密度之間的關系式為B~(ρω)1/2,這與本文討論的類似關系在定性上是一致的. 如果轉動的木星處在太陽恒星的輻射場之中,那么邊界條件要求在木星的表面上輸入遠處太陽的能流密度,這時傳播到木星表面上的輻射波為平面波,表面上的能流密度為I=I0sinθcos(ωt-φ),這里ω是木星的自轉角速度,I0是常數. 星體內部溫度場T(r)滿足的擴散微分方程為[33] (52) 將這一方程的解設為T(r)=R(r)Y(θ,φ)e-iωt,其中D=k/ρc是熱擴散率,其中k是熱導率,ρ是物質密度,c是物質的比熱.分離變量后的徑向微分方程變為 當l=1時,方程(53)的徑向解為 (54) 其中,j1是第1類1階球貝塞爾函數,所以木星內部溫度分布的解可表示為 (55) 其中系數A可以由邊界條件確定,即 (56) 因此星體內部的溫度分布的完整解為 T(r,θ,φ,t)= (57) (58) δT1∶δT2∶δT3∶δT4≈ 1.481∶1.491∶1.493∶1.494, (59) 這時溫度的漲落比值由小逐漸變大,如果木星內部溫度取為T=2 000 K,sc晶格對應的溫度漲落為δT1/T=5%,那么δT1=100 K,此時hcp晶格對應的溫度漲落為δT2=100.88 K,所以不同類型晶格對應的溫度漲落相差都較小. 本文根據泛函積分方法研究了金屬氫的物態性質,在此基礎上進一步研究了木星的流體力學性質,以及磁場和溫度的漲落關系. 本文首先簡述了泛函積分方法在物理學各個領域中的應用,介紹了金屬氫和木星內部的物理性質.其次,本文采用泛函積分方法推導了致密電子-離子系統的壓強和有效作用量,給出了各種晶格作用量的數值計算結果,另外,還導出了液態金屬氫的有效作用量和壓強表達式.隨著壓強的增大,固態金屬氫將轉化為液態金屬氫,其臨界粒子數密度不僅和離子質量M有關,而且很依賴于不同類型的晶格常數Ci,在固體物理中通常的晶格有:sc簡單立方晶格、bcc體心立方晶格、fcc面心立方晶格以及hcp六角密堆晶格. 另外,本文還將金屬氫的物態關系應用于木星的表觀物理性質研究,重點研究了木星的流體力學性質,電磁學和熱力學性質.根據轉動星體的平衡方程的解分析了均勻密度下的粒子數密度漲落,結果發現當漲落δ<0時,星體處于平衡狀態,δ>0時,星體呈現不穩定狀態.本文還根據金屬氫的物態方程推導了修正的Lane-Emden方程,給出了方程的6階級數解,計算了木星的角速度和其密度的比值,結果表明木星的自轉角速度ω對L-E方程的解影響很小,所以計算木星的質量和密度時可忽略角速度這一因素. 本文還采用流體元的運動方程和液態金屬氫的物態關系,估算了聲波的傳播時間的比值,這一比值與不同類型晶格的有效物態參量有關,但其數值僅有很小的差別.另外,在均勻密度星體中磁場強度的漲落和其溫度和晶格常數呈一定的比例關系,4種不同類型晶格對應的磁場強度的漲落比值也比較接近. 本文根據擴散方程的解分析了星體內部的溫度分布,給出了溫度漲落的表達式,結果發現溫度漲落也與晶格常數呈一定的比例關系,在溫度漲落中是負指數,在磁場漲落中是正指數,所以溫度漲落逐漸變大,磁場漲落逐漸變小. 本文主要研究一種理想狀態下的均勻金屬氫星體模型,分析和討論了星體內部的力學、電磁學和熱力學等表觀物理性質,本文的研究結果具有一定的定性意義,對進一步研究木星等巨行星內部的物理性質提供一種研究思路和方法上的啟示.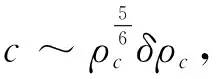
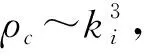
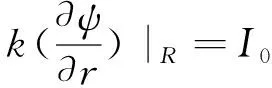
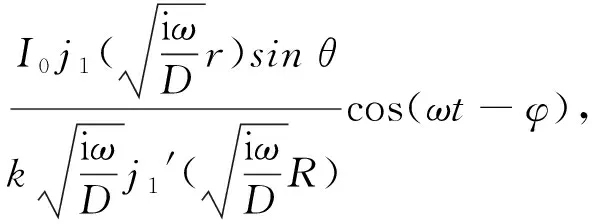
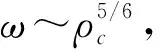
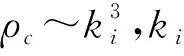
5 結論與討論

