ARIMA模型和神經網絡模型對我國GDP預測分析

李欣祎

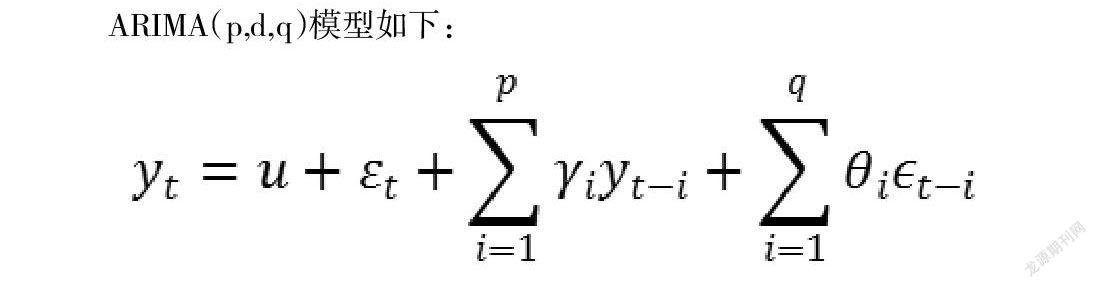
摘 要：國內生產總值（GDP）是衡量一個國家經濟發(fā)展的重要指標，將宏觀經濟發(fā)展現狀量化，研究近幾十年來國家經濟變動趨勢和發(fā)展規(guī)律。本文主要借助ARIMA模型、BP神經網絡兩個模型，選取2000-2019年我國GDP季度數據進行擬合，分別將GDP季度數據劃分為訓練集和測試集，將兩個模型擬合效果進行比較，研究發(fā)現，ARIMA模型的擬合效果較好。最后借助ARIMA對我國2020-2021年GDP進行預測。

關鍵詞：ARIMA;BP神經網絡;GDP

隨著全球化進程的加快，我國綜合國力得到大幅提升。經濟快速發(fā)展的同時，暴露出一系列的弊端，貧富差距分化嚴重，社會矛盾問題凸顯。此時，研究衡量我國經濟發(fā)展的數據指標，對我國GDP的動態(tài)分析和預測對于及時調控國家的政策具有一定的重要意義。當前對GDP的研究主要借助時間序列模型，通過歷史數據模擬未來數據變動趨勢。此外還有借助機器學習算法等，模型操作簡單，易于理解。近些年來，許多學者對GDP進行多方位研究，孫文淵（2015）借助1992-2011年吉林省GDP數據，通過比較傳統(tǒng)回歸模型主成分回歸和機器學習模型神經網絡擬合效果，研究發(fā)現，神經網絡算法模型的預測效果要優(yōu)于傳統(tǒng)主成分回歸模型;李超楠（2018）分別選取用ARIMA和BP神經網絡兩個模型進行分析，研究發(fā)現，兩個模型組合的擬合效果最好，模型準確度較高，可以解決GDP數據中當期和滯后期的隱含的復雜關系。因此，本文選取時間序列ARIMA和神經網絡兩種方法對我國GDP進行分析預測。

一、理論基礎

時間序列通過借助過去存在的歷史數據對未來數據進行預測，研究數據指標的變化趨勢。時間序列ARIMA模型是目前最常用的非平穩(wěn)序列的時間序列模型。在日常生活中遇到的經濟數據，大多都是非平穩(wěn)數據，存在一定的趨勢性和季節(jié)周期性，此時通過差分可以將數據平穩(wěn)，防止出現數據的偽回歸。

ARIMA（p，d，q）模型如下：

其中，p、q表示階數，u是常數，ε代表誤差。

一個完整的神經網絡包括2個過程，首先是輸入層輸入數據，通過計算獲得輸出，如果輸出層輸出和正確數據不一致出現誤差，且誤差超出我們之前規(guī)定的誤差，首先最后一層神經元參數調整，層層向第一層開始調整，直到輸出結果誤差達到最小。本文通過r語言進行實證分析。神經網絡目前主要應用于經濟預測，研究數據之間的非線性關系，操作簡單。

二、實證分析

本文以我國2000-2019年每季度的GDP為研究對象，數據通過中經網統(tǒng)計數據集網站收集和整理得到。

（一）ARIMA模型

1.序列白噪聲檢驗

在對序列進行分析前首先對序列進行白噪聲檢驗，序列通過檢驗后才可以用時間序列分析，從結果來看，序列延遲6階、12階和18階P都小于0.05，根據檢驗原理拒絕原假設，數據不屬于純隨機波動，說明數據存在一定規(guī)律性可以用來分析。接下來利用SAS軟件擬合模型。

2.數據的預處理

首先用SAS軟件畫出2000-2019年全國GDP時間序列圖，發(fā)現2000-2008年GDP增長速度較為平緩，而從2009年以后每年增長速度迅猛。從總的趨勢來看GDP增長呈現指數增長的趨勢，說明這個序列具有非平穩(wěn)性。由于序列具有指數趨勢的序列特征，在時間序列中為了消除這種指數趨勢通常把數據進行對數處理。把原序列進行對數處理后記為lnGDP。

經過對數處理后的序列呈線性增長，序列仍為非平穩(wěn)序列l(wèi)nGDP序列進行差分處理來轉化成平穩(wěn)序列。把2000-2016年的GDP數據作為訓練樣本，2017-2019年的GDP數據作為測試樣本對模型測試結果進行評價。記序列l(wèi)nGDP進行一階差分后的序列記為dlnGDP畫出時序圖如圖1所示。

從圖1可以看出dlnGDP序列在某一值附近波動可以認為此時序列平穩(wěn)。通過時序圖判斷具有一定主觀性，為了更進一步檢驗序列平穩(wěn)性，利用SAS軟件對序列進行自相關偏自相關檢驗。經檢驗發(fā)現此時p值均小于0.01，表明此時dlnGDP序列是平穩(wěn)序列。

3.模型建立

為了找到模型的最佳階數，通過對自相關圖和偏自相關圖進行判斷。序列經過一階差分后達到平穩(wěn)狀態(tài)，然后分別做出序列dlnGDP的ACF圖和PACF圖。

從ACF圖可以看出1階之后全部沒有超過標準差，且衰減程度慢可以判斷自相關系數拖尾。從偏自相關圖中能夠看出，除了延遲1階和7階的偏自相關系數顯著大于2倍標準差之外，其他偏自相關系數都比較小，所以考慮構建疏系數模型，綜合考慮前面的差分運算，擬合疏系數模型ARIMA（（1，7），1，0）。使用條件最小二乘估計，確定模型為：

4.模型檢驗

模型顯著性主要檢驗模型殘差序列是否白噪聲序列，可以得到誤差序列延遲6、12、18和24階都大于0.05不能拒絕原假設，認為殘差序列屬于白噪聲序列即模型顯著有效。

5.模型預測

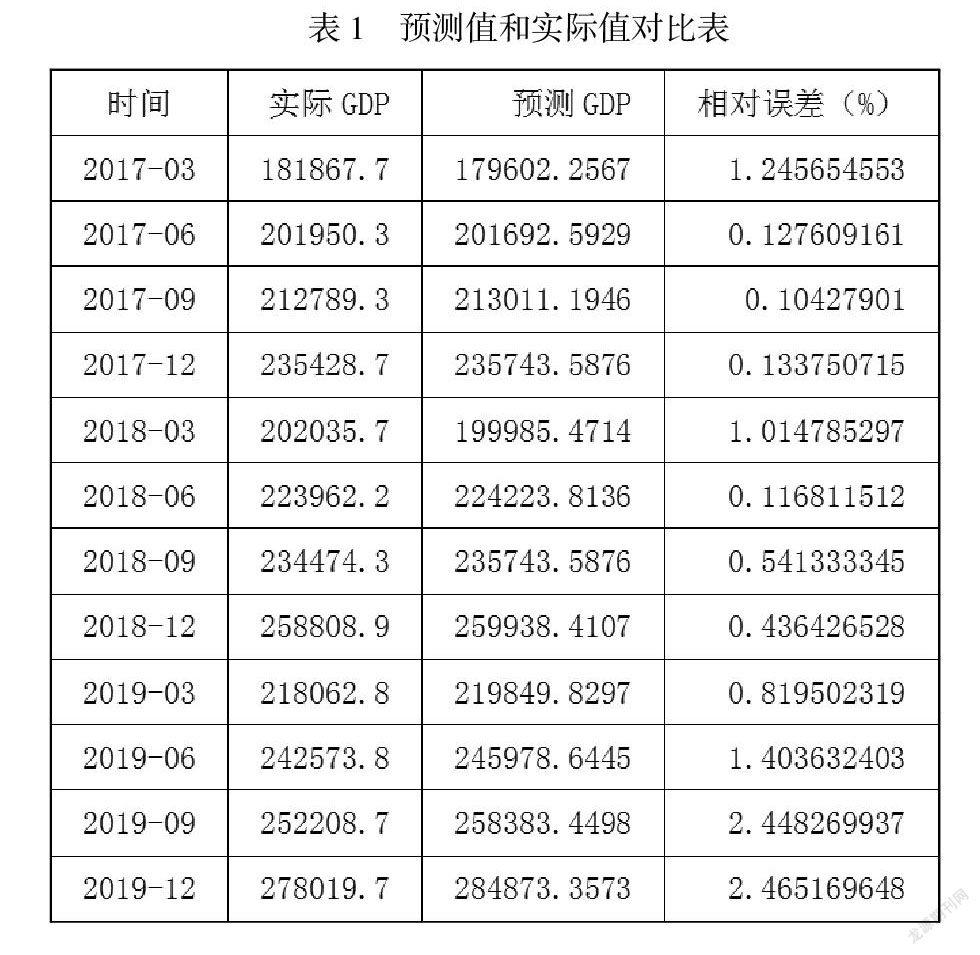
把預測值和實際值進行對比表1：

2017-2019年每季度GDP的相對誤差都在3%以內，三年的平均絕對百分比誤差為0.90%，模型擬合效果較好，模型可作為全國GDP短期預測模型。

（三）BP神經網絡

將所需的數據和相應的程序編寫完成之后，運用R軟件進行分析，得到相應的預測結果，由于神經網絡的預測結果每次均不相同，所以取5次結果的平均值，如表2所示。

觀察得到預測效果理想，BP神經網絡預測值和實際值誤差在10.5%以內，且預測誤差均值為6.7%，但是由表中同樣可以看出，隨著時間增加，誤差逐漸增大，BP神經網絡模型可以很好的預測短期內的GDP，但是長期而言，誤差逐漸增大。BP神經網絡通過調整不同的參數，輸出不同的擬合值，且同一個參數，多次重復也會輸出不同的擬合值。因此，選取不同的參數對實驗結果影響較大。

（四）ARIMA模型與BP神經網絡模型擬合結果對比分析

為了更好的檢驗組合模型預測效果，分別計算ARIMA模型與BP神經網絡模型擬合結果的相對誤差百分比。比較ARIMA模型與BP神經網絡模型兩個模型的相對誤差，可以發(fā)現ARIMA相對誤差比BP神經網絡模型相對誤差小，并且在穩(wěn)定性方面表現最好。

（五）預測

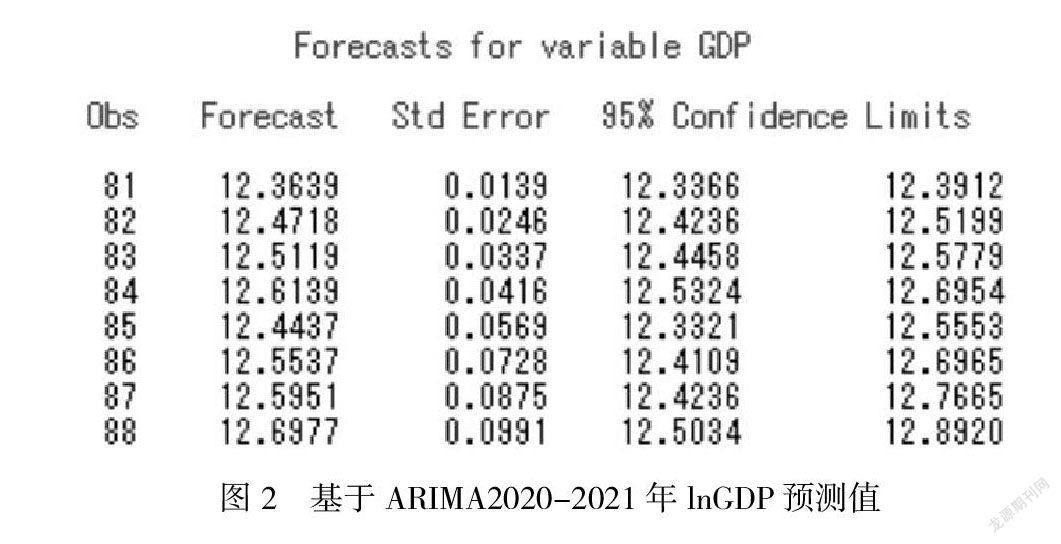
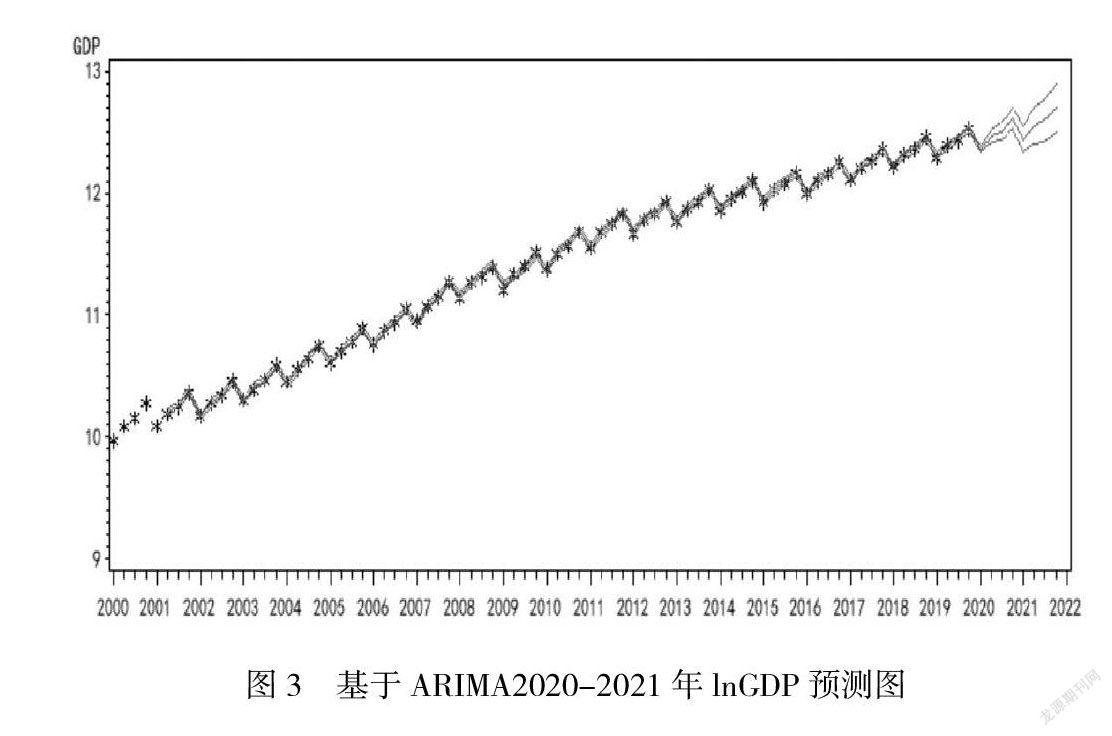
利用ARIMA模型對2020年-2021年8個季度的對數GDP進行預測。圖為lnGDP預測值，紅色線表示預測值，綠色中間部分表示95%的置信區(qū)間，具體lnGDP數值如圖2，隨著時間推移，預測結果波動范圍逐漸擴大，誤差逐漸增大。總體可以看出GDP呈現規(guī)律上升態(tài)勢，但預測誤差越來越大。

三、結論

ARIMA 模型和 BP 神經網絡模型都可以用來預測GDP，并且被廣泛使用，本文采用通過誤差百分比方式來比較模型的預測精度。首先通過結合我國GDP數據特點首先基于傳統(tǒng)的時間序列 ARIMA 模型對我國GDP進行擬合預測，提取當前期與滯后期的線性關系。根據自相關和偏自相關圖結合疏系數選取最優(yōu)的ARIMA（（1，7） ， 1 ， 0）模型來擬合2000年到2016年我國 GDP，根據該模型預測出2017年到2019年我國GDP數據，計算其平均絕對誤差為0.90%。其次利用神經網絡預測特點用 R 軟件構建起 BP神經網絡結構，結果ARIMA模型預測精度明顯高于BP神經網絡模型，說明ARIMA模型預測效果較好。借由最終選取的模型，對2020-2021年每季度GDP數值進行預測，并得到結果。

參考文獻：

[1]孫文淵.基于BP神經網絡模型下預測吉林省GDP[D].延邊大學，2015

[2]李超楠.幾種山東省 GDP 的預測方法及其比較[D].山東大學，2018

[3]蔡淅韻.基于ARIMA模型的國內生產總值預測[J].科技傳播.2020（5上）： 40～41

[4]羅森，張孟璇.基于ARIMA和VAR模型的我國季度GDP預測比較[J].現代商業(yè).2019（35）：50～52