一種基于信息素圖的無人機高效通信覆蓋方法

任少睿,陸忠梅,2,*,石遠明,李立欣,陳巍

1.清華大學 電子信息工程系,北京 100084

2.貴州電子信息職業技術學院,貴州 556000

3.上海科技大學 信息科學與技術學院,上海 201210

4.西北工業大學 電子信息學院,西安 710129

隨著信息化的不斷提升,無線數據通信被越來越廣泛地應用在實時監控、調度監督等方面。在難以使用基站方式通信時,特別是遭遇洪水、地震等急需信息接收渠道的搶險救災時刻,或是應用于保衛戰爭等特殊用途,借助無人機(UAV,Unmanned Aerial Vehicle)進行通信覆蓋都是一種高效的方式。而這些實際運用,對于無人機自組織的飛行網絡提出了靈活性、低時延及長續航、安全性等方面的要求。本文研究的主要問題,是在無人機數量相比于待覆蓋面積較少,也即無人機平均密度較低情況下的無人機群通信覆蓋方法。

目前無人機協同航跡規劃中,集中式和分布式是主要采取的2種方式。對于集中式方法,需數據處理中心對所有無人機獲取的信息進行分析并做出決策,這使得無人機無法自主進行航向選擇而需作為數據處理中心的依附,進而使應用中增加了數據處理中心的限制及無人機群靈活性的約束。相比于集中式方法,分布式方法中無人機的運動不受數據處理中心的制約,更具靈活性。

目前的分布式方法中,基于深度強化學習的協調控制方法具有較強適應性,但這一方法的分布式建立于前期大量訓練的基礎之上。基于變量一致性的梯度下降算法(DGD),通過計算目標函數梯度,能較為高效地得到無人機規劃結果。但目前此類分布式方法不能方便地處理異步問題,計算目標函數的梯度有時難以完成。同時受系統個體間通信時延的影響,其最終結果在收斂性上仍存在需繼續研究的問題。基于分布式模型預測控制(DMPC)的方法在假設無人機間解耦的條件下能夠完成分布式的要求,但該方法需假設無人機間的全連接,因此同樣面臨著無人機間可能出現的不同步而帶來的問題。在無轉角限制條件下,采取臨近處信息素圖(Pheromone Map)驅動能較快給出結果,是一種可行的方式。但從其續航性能而言,因機載能源的有限性限制了無人機的續航能力,為提高無人機的續航能力,在無人機機載能源不變的情況下需降低其平均能耗。而無人機在運動中單位時間能耗隨著航跡轉角增大而迅速上升,無人機行進相同距離的轉角,也即無人機允許的轉彎半徑將受到限制。對于采取臨近處信息素圖驅動得出的最優航向中,因存在對于無人機進行快速轉彎的需求,需對機載能源提出較高要求。

無人機通信覆蓋方法中,將區域進行劃分,借助信息素圖,使無人機群能夠自主規劃行進路徑,因與其他技術結合性好而成為常用方法。另一方面,目前無人機通信覆蓋分布式方法大多未考量物理層中無人機實際航行的安全性需求。對此,若采取壓制干擾方式,對無人機有源大功率輻射提出了要求,不利于無人機的續航能力；依靠航跡欺騙等手段在一定程度上優于壓制干擾,但目前仍主要處于理論論證階段；多無人機協同干擾能取得較好效果,但對單位覆蓋面積的無人機數量需求將大幅上升。

為提高通信覆蓋效率,考慮無人機靈活性、低時延及長續航、安全性的要求,提出一種基于信息素圖的多無人機通信覆蓋方法。首先分析實際應用場景以獲得無人機運動的解耦條件,通過引入地面錨節點(Anchor-node)、限制無人機轉彎半徑、增加地理價值描述函數等方式滿足前述要求。然后設計了無人機運動的收益函數及航向選擇方法,最后以小范圍內無人機收益最大作為目標進行仿真,優化待覆蓋區域重訪時間,提高通信覆蓋效果。數值計算表明,所提出的方法優于無地理價值描述的覆蓋方法,且具有較高的執行效率。

1 問題假設及流程

本文研究問題可表述如下：在給定區域內,給定無人機數量,其滿足無人機密度較稀疏的條件,同時在保證無人機轉彎半徑存在下限的前提下,如何達到最優的無人機自組織覆蓋,使得區域內各點接入時間間隔盡可能小且均勻。

1.1 問題說明

前述無人機密度較稀疏,一方面對應于部分實際任務中,待覆蓋區域極短的接入時間間隔的收益,與付出的代價相比較低,如交通狀況數據搜集等,其對于通信更新頻率的要求不高,不必調用過多無人機；另外,在搶險救災等特殊應用中,短時間調集大量無人機也存在實際困難。對于確需較高無人機密度的應用場景,請參考4.5節中的討論。

實際中,無人機的爬升率對于其飛行性能同樣有較大影響,飛行高度不同,其對地面的有效覆蓋范圍也不同。平原、丘陵地帶的地面起伏在200 m 以下,有限大小的待覆蓋區域內起伏約幾十米,這與無人機數百米的飛行高度相比基本可作為一平面。以大疆Phantom 4 RTK 無人機的實際數據為例,當飛行高度為250 m 時,其可保持0.1 m 的懸停精度。此外,與水平運動相比,無人機爬升的能耗更高,因此在不必要的情況下減小爬升率有利于延長其飛行時間。假設各無人機在各不相同而差別很小的高度上做平面運動,保證了無人機之間不會發生碰撞,無人機的能耗只與其在水平面上的轉彎半徑相關,且其有效覆蓋范圍近似是一個常數。對此方面,進一步討論請參考4.7節。

為保證安全性,無人機僅接收信號而不進行信號的發射,同時無人機僅需其與周圍待覆蓋區域內錨節點的相對位置而不需絕對坐標,是一種代價小,效果相對好的隱蔽方式。同時,2.2節中的地理位置,3.2 節中的覆蓋收益、信息素值等,都是針對于地面錨節點而言的,也即對無人機而言,其覆蓋的目標即為待覆蓋區域中的錨節點。

根據上述分析,對模型做出如下假設：

1)平均而言,待覆蓋區域內無人機密度稀疏。

2)各無人機在差別極小的不同高度上做平面運動,保證不會相撞的同時可以忽略此高度差。

3)無人機轉彎半徑存在下限,保證其續航能力。

4)存在地面錨節點,保證無人機運行安全性。

5)小范圍內無人機航跡曲率近似不變。

1.2 流程架構

將本文討論的方法稱為相對位置的信息素圖方法,方法中物理層地面錨節點完成信號的發送,同時根據相對位置及當前位置錨節點密度給出當前錨節點的地理價值(即2.2節向導信號中的函數)。對于航跡規劃而言,無人機接收地面錨節點的向導信號,以預設的價值函數為依據,選擇小范圍內價值函數最大的航向行進。

其理論流程如圖1所示,可抽象為：整個決策過程對時間進行離散化,在每個離散的時間內,各無人機依靠機載計算系統及預先設定的價值評價方式,通過對所需地點信息素的感知,計算并比較不同允許路徑下,綜合考量一段時間后的行進位置所獲得的收益期望,選取收益最高的最優解行進。地面錨節點不斷進行信號發送,當信息成功被無人機探知,則更新信息素記載,周期性運轉,直至覆蓋任務完成。

圖1 算法模型流程圖Fig.1 Flow chart of algorithm model

2 物理層及信號交互

2.1 物理層地面錨節點

本文所提出的相對位置的信息素圖方法的物理模型示意如圖2所示。

圖2 物理層模型示意圖Fig.2 Schematic diagram of the model

為滿足無人機通信,待覆蓋區域的各錨節點上均存在信號收發裝置,而無人機上攜帶有信號接收裝置以獲取地面信息。為方便起見,將用于常規通信的信號稱為通信信號,將用于為無人機行進選擇提供判斷依據的信號(即攜帶信息素信息的信號)稱為向導信號,通常向導信號比通信信號更加簡單,也更容易擴大向導信號的傳播范圍。

地面錨節點的信號收發裝置一方面依靠無人機與外界通信,另一方面則判斷是否成功依靠無人機完成通信,以不斷更新向導信號。隨著地面錨節點向導信號及通信信號的不斷更新,與無人機的不斷移動接收地面信號,整個無人機與地面錨節點系統將周期運行。

對地面錨節點及無人機間信號接收成功與否的判斷方法而言,無人機可接收地面的向導信號并測定發射該向導信號的錨節點所在區域或位置,如應用與向導信號本身無關的基于圖像識別技術的雙目視覺技術及模糊測距技術,或采取適合于無人機所需探測方向的、有強定向性的側射式天線陣,使用AOA(Angle of Arrival)技術,配合檢測信號強度在信號傳播過程中的自然衰減,即基于RSS(Received Signal Strength)技術,同時依據無人機飛行高度恒定,得到相應地點等。而對于地面錨節點而言,判斷其發送的信號是否被無人機成功接收,同樣可以采取上述雙目視覺技術等。當無人機接收到地面錨節點信號,則可計算得出當前時刻應該選取的飛行方向,地面錨節點也根據當前無人機的位置更新該點的信息素值(若被覆蓋則清零,未被任何一個無人機覆蓋則繼續增加)。時間單位的長度可根據無人機覆蓋范圍大小、地面錨節點密度以及無人機飛行速度選擇,使得系統一方面保持較快的更新速度,另一方面不會做過多不必要的計算。

該方法采取分布式的信息處理與航向控制,同時信息素地圖的存儲亦不占用無人機內存,而儲存在地面各錨節點的信號收發裝置內。

2.2 向導信號P 函數的獲取

為描述待覆蓋區域內不同點的位置不同,同時避免使用錨節點之間的絕對位置以保證安全性,引入函數,稱為地理價值描述量。對應于實際待覆蓋區域內各點,函數的值有所不同。其計算表達式為

式中：為對應待覆蓋區域的點集；為對應于以對應點為中心、半徑等于向導信號的有效接收半徑的點集(實際中信號自然傳播可采取圓形)；取模運算為計算其內部點集的元素數量,即面積度量,以一無人機覆蓋面積為單位。實際中,地面錨節點可根據接收半徑(向導信號有效接收半徑)內各錨節點所發向導信號的強度之和得到本地對應函數,如圖3所示。

圖3 向導信號P 函數有效接收半徑示意圖Fig.3 Schematic diagram of effective acceptance radius of P function of guide signal

特別地,在仿真中采取了方形的有效區域,是為在保證計算簡便性的前提下檢驗函數的有效性。事實上,在物理層中這一計算遠比仿真中所需要的簡單。同時,為避免混淆待覆蓋區域內不同點的函數值,仿真檢驗中以“矩陣”表示不同點的函數按照其位置排列而構成的矩陣。

無人機可采取基于RSS與AOA 結合的定位方法,受無人機轉彎半徑有下限的影響,本模型無人機所需要的信息素并非均勻分布在當前無人機位置的四周,而主要集中在當前運動方向前方,故而與基于天線輻射特性與接收天線方向特性的側射式天線陣適應良好。

另一方面,地面錨節點的向導信號更新,亦可同樣采取雙目視覺等技術,對周圍無人機距離進行測量,當存在無人機距當前錨節點小于通信信號接收半徑時,可認為無人機已經將該錨節點的信息收集,向導信號可隨之變化。

此外,函數可認為是一個動態變化的函數：當地面某一錨節點被摧毀,根據函數的獲得方式,臨近錨節點由于接收不到已被摧毀錨節點的向導信號,將會改變臨近地點函數的具體數值。考慮到被摧毀的錨節點處雖然仍需覆蓋,但由于缺少信號發射設備而喪失了覆蓋的實際意義,故而這種動態變化有利于無人機有效覆蓋效果的提升。

3 無人機航跡規劃

3.1 無人機間運動解耦分析

多無人機系統需要考慮無人機之間的相互影響,但在該問題下若能對無人機之間運動解耦,則各無人機之間的影響作用可以只通過地面錨節點的信息素大小做間接的描述,而忽略其間的直接交互。即無人機之間并不是沒有關聯,其通過改變地面錨節點信息素來對其他無人機的運動產生影響；但因不需要再單獨計算無人機之間的直接作用,所以可以簡化推導,降低實際無人機航跡規劃中的計算量。

接下來討論無人機間運動解耦的限定性條件,這一條件也是本文達到分布式目標的充分條件。通過推導出各時間單位內,無人機之間發生直接相互影響的概率足夠低,說明在無人機密度稀疏的假設下忽略無人機之間的直接相互影響是合理的,具體推導如下：

設每時刻無人機能覆蓋的范圍半徑為,因本方法假設只考慮無人機在一恒定高度上運動,則兩無人機之間發生直接相互影響需間距小于2。若無人機確實“均勻”地運行,即對于所有無人機而言,其在待覆蓋區域上空的分布是均勻的,速度方向也是均勻的,設其大小為,那么對于一無人機而言,其他無人機的速度方向與此無人機的速度方向正交,無人機間的相對速度平均為

此時無人機均勻分布在整個待覆蓋區域內,密度為

式中：為對應于待覆蓋區域的點集；取模運算如前,為計算其內點集的元素數量,即對應的面積度量,以無人機覆蓋面積為單位。因此平均而言,該無人機與其他無人機覆蓋區域相互交疊的頻率為

在一個時間單位內,該無人機的覆蓋區域沒有和任何一個其他無人機的覆蓋區域發生交疊的概率滿足：

考慮到實際中無人機并不是均勻分布在待覆蓋區域中,無人機之間的速度方向也不是完全正交的,因此實際應該將相對運動速度修正為,頻率修正為。因這一修正與無人機均勻性相關,則將與3.4節引入的參量相關。因此,無人機實際航行產生的值越接近于無人機均勻分布時所得到的值,則可以認為無人機越接近均勻分布,上述修正將越小,原公式與真實情況越相符,具體參量的引入在3.4節中進行。但即使需進行一定修正,由式(6)可知,與單位時間的長度、無人機密度的關系仍滿足：當足夠小時,趨于1。在時間單位長度確定時,無人機密度越小,將越接近于1。因此當無人機稀疏分布于待覆蓋區域上空時,可近似認為到下一時刻之內,無人機間所允許的各路徑均已解耦,無人機的運動不受其他無人機運動的直接影響,而僅需考慮接收到的地面信息。無人機運動解耦的假設,也是本文分布式計算的前提。事實上即使兩無人機相距較近,兩無人機也均會因受另一無人機已改變的地點的向導信號影響,而傾向于背離另一無人機行進。

經上述推導可知,時間單位長度不變時,隨著無人機密度的提升,無人機的覆蓋區域之間不發生交疊的概率將降低,不再滿足解耦的條件,因此本模型難以直接應用到這種情況,對應討論在4.7節中進行。

3.2 無人機航向及收益

參照圖4,無人機決策依據系當前無人機從行進前方的小片區域內獲知的向導信號。時間離散處理后,計算中無人機簡化采取圓弧運動,而實際無人機運動為平滑的運動,這一點在離散時間的間隔趨零時得以過渡。每個時間單元內,無人機接收到前方所需區域(即圖4中各預測軌跡末端連線內部,虛線所示)的向導信號,其攜帶有根據當前時刻距上一次該點被無人機覆蓋的時間間隔,及該點周圍錨節點密度,得到的覆蓋該點的收益信息。因對于無人機的航行轉角有限制,在每個時間單元內無人機航行距離與運動方向轉角均較小,可將允許選擇的航向轉角離散處理。為保證離散得到的結果準確,可根據式(7)計算待選可行路徑的數量,并據此得到各路徑的曲率半徑。實際計算中,無人機對比各可行路徑的收益,選擇最終的行進航向。

式中：為離散處理后待選擇路徑的總數,圖4中為5；為一個時間單位內無人機可移動的距離,圖4中為沿著無人機航向對比軌跡,從無人機當前位置到航向對比末端的距離；為無人機允許的最小轉彎曲率半徑；引入作為可調整的比例系數,同時用以調整量綱。

圖4 無人機所需信息素對應區域及待比較路徑示意圖Fig.4 Corresponding area of pheromone and path to be compared for UAV

當?時,根據幾何關系,最小曲率的航向對比軌跡的末端與沿當前航向直行的軌跡末端距離近似為/,待選航向數應與此距離成正相關,以使得最終航行至軌跡末端時,不存在某點在各軌跡之間卻不能被任何一軌跡覆蓋的情況。簡化地對二者取線性關系,對應的各個待選航跡的實際曲率半徑使最終相鄰兩航跡末端距離相等,也可根據式(7)等價地計算出。

考慮允許的轉彎有左右2個方向,以及直線航行,最終得到離散處理后待選擇路徑的總數滿足式(7)。其中?的條件,在單位時間長度不斷減小時可滿足。實際中系數(忽略單位)應至少大于1,以減小離散處理轉彎半徑對實際的影響,但為減小計算量也不宜過大,在本文最終的仿真檢驗中已取=2。

對于無人機不同路徑的收益,采取如下分析：

首先,若將信息素均勻分布到無人機行走至信息素所在地的路徑上,直到無人機行經該點,獲得的信息素量相等,付出代價也相同(若將耗費時間等因素視為代價的話)。也即,單位行進(或者說單位代價)相應等效獲得的收益,即

式中：為這一路徑的收益；為對應行經地點的當前信息素價值(假設信息素隨時間線性增長,為保證覆蓋的均勻性,信息素價值與信息素本身的數值可以有所不同)；Δθ為當前轉彎半徑下,行經該點的速度方向與初始點速度方向的夾角絕對值；為小范圍內行進軌跡的曲率半徑,近似為一常數。

式(8)中的物理意義與信息素數值共同反映出來。信息素的數值對應了當前地點距離上一次被覆蓋的時間長度,即接入時間間隔。為使無人機覆蓋效果較好,應該使盡可能小,也即使無人機在相同時間內獲得的盡可能大。因此信息素平均值反映了接入時間間隔的平均值,信息素極大值反映了接入時間間隔的最大值。而是時間長度與覆蓋均勻度兩方面綜合考慮的描述參量,當對于某一地區進行無側重點的通信覆蓋時,一方面希望所有地點接入時間間隔的平均值最短,另一方面希望避免雖平均接入時間間隔較短,但存在某些地點長時間一直未被覆蓋的情況。為避免第2種情況的出現而引入,因此與相關,但其數值可以有所不同。

同時在實際情況中,無人機移動的意義包括2方面：其一系收集行經地點的信息素,這一意義在上述參量中得以體現；另一方面,無人機從一點移動至另一點,其空間位置發生的改變,因周圍環境存在差異(如周圍錨節點密度不同),而對接下來無人機的行動收益產生潛在影響。根據該點的位置與周圍環境,2.2節中已引入描述函數,來表現這種行進位置的意義。

表征了發射向導信號點位置的影響,也即地理價值描述量。這一參量的引入是本文提出的方法對基礎信息素圖方法的拓展,也是將該方法命名為相對位置的信息素圖方法的原因。

函數為無人機的等效收益函數,該函數表達式為

是決策的依據,無人機將選擇等效收益最大的路徑行進。對于信息素價值的增長,也即的增長方式,嘗試不同函數形式,以達到最優效果。

3.3 信息素增長及飛出損失

地面各點信息素,簡單地可將地面做同樣大小的網格分割,認為每個網格內存在一個錨節點,并構建對應各網格的矩陣,以其元素值反映各點信息素,即物理層中假設地面錨節點網格狀均勻分布在待覆蓋區域內。

假設各點信息素每一單位時間增加一個單位,則信息素值可反映當前點的2次接入時間間隔,而式(8)中出現的、無人機實際使用的信息素價值無需隨時間線性增加。實際中可根據具體需要,決定關于的函數形式,這里對比以下2種常用函數形式,即

式中：為一定值,信息素隨時間線性增長。根據仿真結果來看,為較好地滿足通信覆蓋均勻性的要求,需使的增長呈非線性。當然,無需預置這一點。

在待覆蓋區外,可增加飛出損失,相應取信息素價值為負即可,這使得無人機能快速返回待覆蓋區域。但不宜禁止無人機飛出待覆蓋區域,否則在待覆蓋區域與外界的交界處,覆蓋效果將受到損害。在實際中可調整函數的具體形式,使得邊界處收益迅速下降即可達到相同效果,或擴大錨節點布置范圍亦可。因仿真檢驗中該量恒定未變,為一無關變量,在此不多贅述。

3.4 無人機覆蓋評價及R 參量

接下來推導無人機通信覆蓋中,不存在轉彎半徑約束下的待覆蓋區域內信息素最優結果的上界。以方形的待覆蓋區域為例,假設無人機的行進軌跡是最優的,設該狀態下待覆蓋區域內各點的信息素數值構成一隨時間變化的×的矩陣。令與相同,記所有元素中的最大值為,所有元素的平均值為,中最大值為,所有元素平均值為,仿照無人機覆蓋對矩陣更新,矩陣則每次均選擇信息素最大的點覆蓋。第一輪,對所有無人機而言,下一刻中被清零的點數值之和及中最大的個元素之和應滿足：

且此時有：

依此進行輪,直到第+1輪執行時,對于中最大的個數值,至少存在一個數值的對應位置在輪內已取得一次,且是輪內第一次取得重復位置。則可知整個待覆蓋區域內,當前情況下覆蓋的間隔將不大于。且在前輪中,不等式(13)和不等式(14)恒成立(但不等式(12)可能在某些步中不成立)。因每點信息素隨時間而線性增加,實際時間的變化(也即輪數的增加)不影響最終與的相對值,而僅受到最開始各點信息素初值的影響。

從初值均為0開始遞推推導,并對各、取上界,可導出(在待覆蓋區域面積能整除無人機數時。否則最終數值不會穩定在一個值上,而會有微小波動,但不會偏差過大)：

當度量單位取為單個無人機的覆蓋面積時,則只需除以無人機數量即得結果,因此式(1)也保持了這一單位的選取。、為考察時間無限長時所得最優覆蓋效果的上界,同時也是無轉彎限制條件下,無限長時間的平均最優覆蓋效果。實際覆蓋得到的(,)與(,)相比,可以一定程度上反映該模型的覆蓋效果。當然不同情況下,對于與兩者的重視程度也可能不同。與在最優情況下,滿足：

用來表征上述比值,最優情況下=2。但實際中,受到待覆蓋區域內某些點臨近邊界,特別是位于具有較大轉角的邊界處時,覆蓋該點可能需要飛出待覆蓋區等,代價較大,無人機趨向于轉彎返回而非將其覆蓋。相應的,可以用與2的接近程度來表征覆蓋的均勻性。

對于無人機密度較高時的值增長,可如下解釋：當無人機密度較高時,由于此時無人機間運動發生直接相互影響的可能性已很高,不能通過忽略這一影響使得無人機間的運動解耦。此時若仍認為無人機之間的運動解耦,而對各無人機進行單獨的航跡計算,將可能出現同一地點同時被多個無人機覆蓋的情況。考慮極端情況：即此時存在2架無人機,下一刻都可能覆蓋當前信息素最大的2點。若考慮無人機之間的直接影響,下一刻信息素最大的2點將被2無人機分別覆蓋,在這種情況下也是符合前述理論分析的,因此值仍為2；當認為無人機之間運動解耦,而只考慮其間的間接影響時,2無人機都將覆蓋信息素最大的一個點,而遺漏了信息素第2大的點。由于未減小待覆蓋區域的面積,因此這一遺漏點對于信息素平均值的提升不明顯,但該點下一時刻增加的信息素卻全部作用到了極大信息素上(也即上)。故此時應用本文方法將導致值比理想情況下的值大,且無人機密度越大,上面的分析涉及的信息素最大點的數目就可能越多,也越偏離理想情況。一方面,上述值的增大反映了覆蓋均勻性下降,另一方面,因無人機重復覆蓋同一點而遺漏其他點將使得平均接入時間間隔上升,即總體而言應用本文方法所得到的覆蓋效果與最優情況的差距隨無人機密度增大而增大。

本文中,考慮到整個待覆蓋區域重要程度是相同的,因此最終調整各函數形式,使得盡可能接近2。在變化不明顯時,比較(,)與(,)的數值。在本問題的背景下,將待覆蓋區域取為50×50的方格(單位為一架無人機可以覆蓋的面積),則依據式(15)和式(16),對應覆蓋效果描述參量、與無人機數量的關系如表1所示。

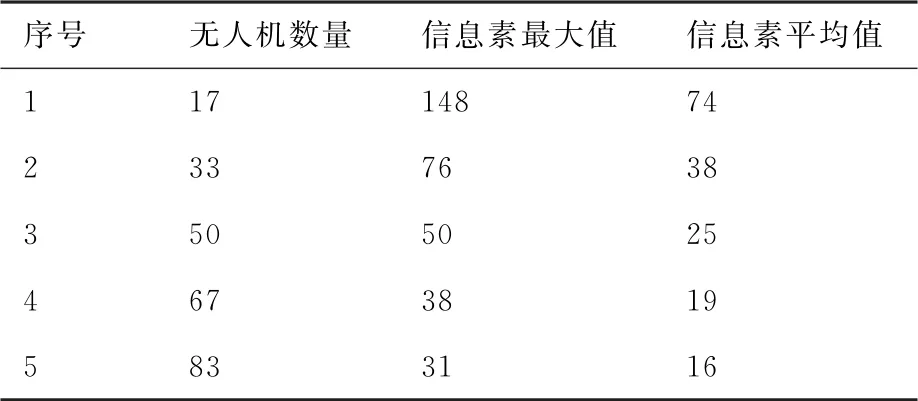
表1 描述參量與無人機數量關系Table 1 Relationship between description parameters and UAV quantity

直觀發現,同樣大小的覆蓋區域,無人機數量極少時,信息素最大值與平均值均極大,也即平均而言,待覆蓋區域需更長時間才能被收集一次信息；而無人機數量較多時,覆蓋效果較好,但此時若繼續提升無人機的數量,覆蓋效果提升不明顯,也即無人機資源被浪費了。同時需考慮到當前模型下無人機稀疏的假設,以保證無人機之間的運動是解耦的。

綜合考量,可選擇無人機數量為50架用以仿真檢驗,無人機轉彎半徑最小取為無人機有效覆蓋半徑的5倍。

4 仿真實驗

依據本文方法進行數據驗證,以判斷其有效性。如上所述,無人機數量取50,則每時刻各無人機可覆蓋面積之和,相較于待覆蓋區域面積小1～2個數量級,基本滿足稀疏的條件,應用本方法仿真。使用各方法所得仿真結果匯總于表2中,以本文方法得到的無人機均勻性描述參量,確實接近于理想無約束條件下計算出的值,可以從另一方面反映這一無人機密度確實基本滿足了稀疏的條件。

表2 各方法仿真結果對比Table 2 Simulation results and data of each model

在效果圖圖5～圖8中,因信息素與上一次被覆蓋至今的時間長度成正比,所以圖中的縱坐標信息素的大小,可認為反映了當前點至其上一次被無人機覆蓋的時間間隔的長短：信息素值越小,則平均而言待覆蓋區域內各點被無人機覆蓋一次的時間越短；信息素最大值越小,說明待覆蓋區域中當前時刻各點距上一次被覆蓋的最大時間間隔越小,也即重訪時間越短。

為方便對比不同方式的覆蓋效果,將各仿真結果及無約束條件下3.4節所得計算結果(即各仿真結果圖中的極值參考界、均值參考界)匯總于表2,仿真結果的圖片及分析在4.1～4.4節中展示,各方法的對比討論請參考4.7節。

4.1 本模型數值仿真結果

本模型中信息素價值的函數形式采用：

以保證能較快達到較高水平,其中取1.082,使、α兩者在50 個時間單位處連續過渡。選擇在此時間單位處連續過度,因其為3.4節計算所得的,在無轉彎半徑約束條件下的覆蓋結果的最大值,也即用以配合在該條件下根據式(15)、式(16)所得數據。同時本模型中使用了2.2節定義的對于地理價值描述的矩陣,來反映待覆蓋區域內不同點即使當前信息素值相同,但因其位置不同,所造成的不同點覆蓋價值的差異。

因持續覆蓋,取不同起末時間進行分析時,求得其平均接入時間間隔及最大接入時間間隔將略有不同。圖5～圖8中圓點線、菱點線為根據式(15)和式(16)所得無轉彎半徑約束下的無人機覆蓋效果描述參量、,此二值作為衡量的參考基準線,分別稱為極值參考界、均值參考界；星點線表示當前時間所有地塊信息素的平均值；方點線表示當前時間所有地塊的最大信息素。本文方法在兩者基本穩定后,信息素平均值、信息素極大值分別在47及159左右波動。

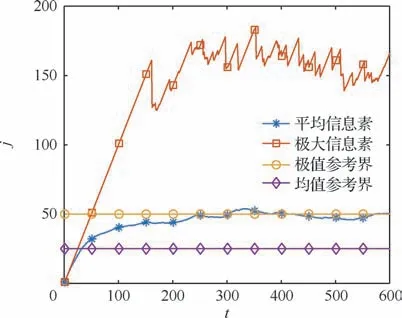
圖5 本模型覆蓋效果圖Fig.5 Covering results of this model

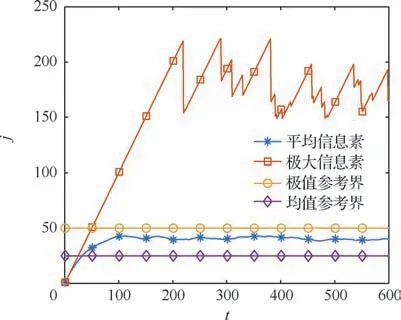
圖8 j取正比例函數覆蓋效果圖Fig.8 Covering result when j is a positive proportional function

4.2 無地理價值數值仿真結果

信息素價值的函數形式仍采取式(18)的形式,但未引入地理價值的情況下,即式(9)中無人機的等效收益函數改為

所得仿真結果見圖6。與4.1節對比,其平均信息素與極大信息素分別在50 及170 左右波動。與此相比,4.1節中兩代表量47及159反映的平均接入時間間隔與最大接入時間間隔分別提升了6.4%與6.9%。特別是對于信息素全時段最大值,4.1節結果在180左右,而4.2節中接近200。因此對于假設無人機稀疏的本文方法而言,增加矩陣來反映待覆蓋區域內不同點因位置不同而產生的差異,對于提升無人機的覆蓋效果確有作用。

圖6 無地理價值描述覆蓋效果圖Fig.6 Covering results without description of geographical value

4.3 半隨機方向數值仿真結果

圖7為無人機在允許的轉角范圍內隨機挑選一方向行進的覆蓋仿真結果。其全地塊最大信息素在400個時間單位內持續增加,遠差于4.1節的效果；其全地塊信息素平均值在500個時間單位后仍存在上升趨勢,約54。4.1節中本文結果與之相比,平均信息素指標(即平均接入時間間隔,因信息素隨接入時間間隔線性增長)提升約15%。

圖7 隨機取向覆蓋效果圖Fig.7 Covering results of random orientation

本節信息素最大值在4.1 節結果的2 倍以上,且本節中這一數值波動幅度很大,4.1節中信息素最大值在仿真到200 個時間單位時基本穩定。因此,隨著仿真時間的延長,這一比值可能繼續增大。事實上,在無人機臨近待覆蓋區域邊界時,本節仍采用了4.1 中的模型,故稱半隨機方向。否則,若允許無人機飛出該區域,采用完全隨機方向,仿真結果顯示其極容易飛出當前區域,而導致幾乎沒有任何覆蓋效果。

4.4 j函數形式的影響

圖8為存在地理價值描述,函數形式為正比例函數的仿真結果。其所有地塊信息素的平均值比4.1節中略低,在40左右,該結果比4.1節中本文方法所得結果略好,但信息素全時段最大值遠高于4.1節中對應數據(最大到達220以上,而4.1節在180以下),且表現出較大的波動性。

計算4.1節與4.4節2方法所得值以對比2方法對于待覆蓋區域覆蓋均勻性,4.1節對應值為3.8,而4.4節對應＞5.5(這里用大于5.5來描述,是因為4.4節中仿真所得信息素最大值波動大,隨著仿真時間的進一步延長,可能會有進一步增加)。根據式(17),覆蓋最均勻的情況下值為2,可見4.1節的覆蓋效果的均勻性更好。

4.5 無人機稀疏性

本文提出的相對位置的信息素圖方法的使用,建立在無人機數量相對于待覆蓋區域面積較小的情況下,也即無人機較稀疏的情況下。圖9展示了在待覆蓋區域為50×50的方格這一情況下,不同無人機數量的全時段極大信息素這一參量的結果對比,圖10展示了不同無人機數量對應的值,3.4節已計算出理論最優的無人機均勻性描述參量為2。

圖9 不同無人機數量的極大信息素值對比Fig.9 Comparison of maximum pheromone values of different UAV numbers

圖10 不同無人機數量情況下R 值對比Fig.10 Comparison of R values under different UAV numbers

圖9反映出：當無人機密度較低時,極大信息素較大,或者說全部時段、全部區域內的最大重訪時間較長,覆蓋效果較差；當無人機密度較高時,覆蓋效果較好,但此時隨著無人機數量的繼續增加,效果提升卻并不明顯,這與3.4節中的分析結果是相符的。圖10 反映出：當無人機密度較低時,其值基本恒定,在3.7左右；而當無人機密度較大時,值將增長。對于本文所選取的待覆蓋區域而言,可認為值小于4時基本了滿足無人機稀疏的條件。

由此可知,當待覆蓋區域面積較無人機可覆蓋面積大1個數量級以上時(更可靠地需＞2個數量級左右,1個數量級已較勉強),基本可滿足無人機稀疏的條件,應用本文方法能夠得到好的結果。若不滿足上述條件,結合圖9 與表1,以250架無人機分析,不考慮轉彎半徑限制的理論信息素最大值為10,而實際覆蓋效果為50,與理論分析差別較大,此仿真結果也證明,當無人機密度較大時,本文方法將有較大的局限。

當不滿足無人機密度較小的條件時,有以下幾種可能的方式來改進本文中的方法：一是將無人機之間的直接影響考慮進來,此時需增加無人機之間的信號交流,以保證在小范圍內無人機之間的決策是相互影響的,可通過增加無人機之間的排斥等因素來描述無人機之間的影響；另一種可能的方法是重新分析待覆蓋區域,由于此時無人機密度較高,同時分析各無人機的運動情況較困難,可對待覆蓋區域進行計算,得出少量無人機對當前地塊進行覆蓋的方法,其余無人機沿著同樣的軌跡,交錯一時間間隔進行覆蓋。對于需要計算的少量無人機,則轉化為了密度較低的情況。此時并非所有無人機都進行決策,而僅有少量無人機之間進行決策,其他無人機則跟隨其運行。

4.6 算法對比分析

本文中提出的方法在持續性通信覆蓋應用外,對于單次全覆蓋的路徑問題也有一定作用。在邊界不規則或有障礙物時,基于GBNN 算法及受生物啟發的神經網絡算法的覆蓋路徑規劃方法效果圖(局部)見圖11。其中右下圈內為死鎖位置,受生物啟發的神經網絡算法在死鎖處會停留較長時間,而基于GBNN 算法則能立刻脫離死鎖地點。

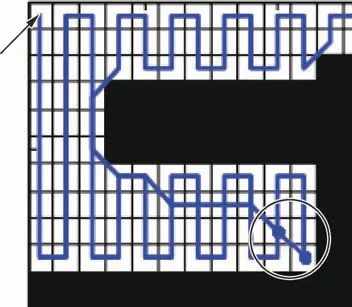
圖11 神經網絡、GBNN 算法UAV 脫離死鎖地點軌跡Fig.11 Paths of UAV escaping from deadlock using Neural Network and GBNN-based algorithm

本文中基于信息素圖的方法,因其行經地點的信息素隨探測時間點至今的時間間隔變長而增大,因此在圖中最右下角的覆蓋死鎖處,探測器(這里不單指無人機)將沿最下方行進到最左側,再向上運動,回到開始箭頭所指處,繼而可以探測右方未探測區域,即圖12中自右下方箭頭標記,沿邊界運行至左上方未覆蓋區域處。

圖12 本文方法UAV 脫離死鎖地點軌跡Fig.12 Paths of UAV escaping from deadlock using present method

在效果上,本文的方法可通過簡單地計算即使得探測器立刻脫離死鎖地點向外移動,協助受生物啟發的神經網絡算法快速脫離死鎖。但其移動至未探測區域所需的距離比GBNN 算法的略長,因此本文方法更適合無障礙物或邊界比較規則的地區進行持續覆蓋,在障礙較多或邊界不規則性很強時,亦可結合GBNN 算法提升覆蓋效果。對于受生物啟發的神經網絡算法,本文方法因計算簡便,也可以作為其脫離死鎖的一個備選方案。

對于本文方法脫離死鎖,有以下幾種可能的方法以縮短路徑耗費：一是改變方法間轉換的判斷依據,圖12對應的轉換依據,是當得出的行走目標與當前點相同時,開始應用本文方法；當下一目標未被覆蓋過時,重新回到受生物啟發的神經網絡算法。若修改為：行走目標與當前點不同時,回到受生物啟發的神經網絡算法,則與GBNN 算法得到的路徑相比,所得路徑僅在脫離死鎖的開始點略有不同,總的路徑耗費基本一致。另一種可能的方法是增加考慮的“步數”,采用分支界限等方法得到較短的路徑,這里信息素圖將為選取最初的路徑提供方向。因實際未必需計算得到最短的結果,可得到一個較短的路徑即返回,則能達到減小計算耗費時間的效果。同時,增加輔助的Dijkstra圖,配合動態規劃的方法得到最短路徑也是可行的,在這一方法中,信息素圖則只作為判斷是否已經覆蓋過的依據。上述3種方法中,改變方法轉換判斷依據效果比直接應用本文方法好,且計算量較小,但不一定能夠得到最短的路徑；采用分支界限或借助Dijkstra圖都能夠得到最短路徑,但計算量大,耗費時間長。實際應用中可以對比計算耗費與探索耗費,決定選擇的方法：若待覆蓋區域較大,計算難度將迅速上升,此時改變方法轉換判斷依據的效果較好；若待覆蓋區域較小,則可選擇采用分支界限或借助Dijkstra圖來減小探測器移動的消耗。

4.7 仿真結果討論

從仿真結果來看,對比4種方法,本文方法的極大信息素值波動最小,穩定性最好。為進一步討論各仿真結果,圖13中4.1～4.4折線對應于4.1～4.4節所描述的方法,展示了本文方法與隨機取向、簡單臨近信息素驅動等方法的覆蓋效果對比。橫坐標“平均值”等表示該方法覆蓋所得各時刻信息素平均值等各參量；縱坐標“相對比值”是以本文方法4.1節所得結果為基準,得出的不同方法的各參量與本文方法所得參量比值,比值越低可以認為覆蓋效果越好。其中,關于隨機取向方法的結果因與其他方法差距較大,為對比清晰,超過上限(相對4.1節結果比值超過1.5倍)的數據已取上限進行繪制。

圖13 各方法覆蓋效果數據對比Fig.13 Comparison of values of different methods.

比較4.1節及4.2節對應折線以說明引入矩陣的影響：一方面,引入矩陣描述了不同地點地理價值的差異,降低了信息素平均值與極大值(即接入時間間隔減小)；但另一方面,引入矩陣使得待覆蓋區域內不同點的覆蓋價值——即使其當前信息素一樣多——對于無人機而言也不再等價,可能在一定程度上導致不同點覆蓋的均勻性惡化。觀察覆蓋均勻性描述參量,圖12中2方法所得參量在保留兩位有效數字的情況下大致都在3.8附近,無明顯差別。說明在這種情況下,使用矩陣在提高平均覆蓋效果的同時,沒有造成覆蓋均勻性的惡化,故對于本問題而言,引入矩陣是有益無害的。

比較4.1節及4.4節對應折線以說明不同函數形式的影響：對比兩折線數據,4.4節的信息素平均值比4.1節略低,但極大值、極大均值以及值都遠高于4.1節的結果,這反映出4.4節的覆蓋均勻性差,不能保證待覆蓋區域內全部點均獲得良好通信覆蓋。從模型假設而言,因其無人機的均勻性差,則即使在無人機平均密度較低的情況下,3.1節中推導某一無人機與其他無人機覆蓋范圍不發生交疊的概率仍可能迅速下降,也即無人機之間有較大的影響,解耦假設不成立。故不論從覆蓋均勻性,或是方法的合理性上,取的函數形式如4.1節都是比4.4節更為優越的。

4.6節的仿真結果也反映在待覆蓋區域邊界極不規則的情況下,限制無人機轉彎半徑可能導致無人機在允許范圍內不存在合理解,此時無人機能耗應作為次要考慮因素,故本文方法不適用于這類問題。

此外,關于模型中無人機飛行高度的問題討論如下：模型假設無人機在一恒定高度上運行,當引入無人機飛行高度這一參量,考慮無人機運動中爬升率等因素時,需重新計算其耗能。不同爬升率下,無人機轉彎半徑的約束也將有所不同。

本文方法需在無人機高度近似不變的情況下使用,實際中減少無人機的爬升與下降也有利于減小無人機能耗,提升無人機續航能力。但增加無人機爬升速率因素,將可能提高其位于待覆蓋區域邊界處的行動效率,在無人機密度較大時進行無人機間的碰撞規避等也有其意義。這種情況下,無人機所能覆蓋的范圍與其高度相關,若無人機高度可變,則矩陣計算時所需的信號自然傳播的有效接收范圍隨之變化。但物理層獲得矩陣也是通過接收到的信號強度得出的(如2.2節所述),將檢測信號強度的主體從地面錨節點變為無人機,可方便地獲取新矩陣。

5 結 論

1)對于降低計算量,克服無人機異步問題,根據多無人機通信覆蓋中無人機較為稀疏的假設,分析了無人機間的運動解耦,保證了利用小范圍信息素圖進行無人機航跡規劃的合理性,并提出了用于檢驗當前情況是否滿足無人機密度稀疏條件的參量。

2)提出了地理價值的描述函數,改進了簡單利用臨近信息素圖驅動的方法,除單純覆蓋收益外增加考慮了無人機位置改變帶來的收益。有利于在不增加計算開支的前提下提高覆蓋效果,同時有利于達到整個區域的均勻覆蓋。

3)增加地面錨節點并約束無人機的信號發送,保證了無人機的安全性；信息素在地面存儲的設計,有利于節省無人機存儲空間。