基于G-N迭代的雙星時頻差定位融合算法

徐英杰， 張 敏， 張文俊， 吳癸周， 郭福成

(國防科技大學電子科學學院， 湖南長沙 410073)

0 引言

星載無源定位系統以其偵察范圍廣、不受天氣氣候影響、觀測站是運動的等優點而受到國內外學者的廣泛關注，目前已被普遍應用于軍事和民用領域。星載無源定位技術中常用的觀測量有到達時間差(Time Difference of Arrival，TDOA)、到達頻率差(Frequency Difference of Arrival，FDOA)和到達角(Angle of Arrival，AOA)等，其中多星時差頻差定位憑借其可瞬時定位及高定位精度的優勢，在對雷達等脈沖輻射源的定位中應用更加廣泛。

國內外的學者對多星時差頻差定位算法進行了大量的研究,但以上研究僅針對單次定位進行改進且衛星使用數量多為三顆以上。文獻[7]指出衛星定位系統在過頂期間會多次截獲到地球上靜止輻射源發出的信號，而有效利用多次截獲的數據進行融合并定位可以提高定位精度并減少成本。

針對多次觀測融合算法的研究，賈興江等人針對雙/多無人機測角頻差系統提出了一種融合多次觀測數據的定位算法，該算法在單次定位的基礎上，引入了批處理加權最小二乘融合算法以及序貫加權最小二乘融合算法，實現了多次觀測信息的有效融合。張莉等人提出了一種在觀測站存在誤差的情況下，運動雙站對巡航目標的時差頻差定位算法，該算法有效融合多次觀測的數據并達到了克拉美羅下界(Cramer-Rao Lower Bound，CRLB)。文獻[7]針對三星編隊過頂期間對輻射源多次觀測，提出了一種基于高斯-牛頓(Gauss-Newton，G-N)迭代的三星時差定位融合算法，該算法僅使用多次觀測的時差信息和輻射源高程信息進行定位。實驗證明該算法定位性能達到了CRLB且優于現有的位置合批處理方法。

本文將在時差定位的基礎上融入頻差信息，提出一種將多次觀測的時差頻差數據與高程信息融合的雙星時差頻差定位算法。具體思路為將不同時刻下觀測到的時差信息和頻差信息融合并結合輻射源高程信息構建代價方程，利用G-N迭代求解非線性最小二乘問題，迭代初值可以通過單次定位粗略得出，在使用相同數據的條件下，獲得比現有位置合批處理方法更高的定位精度。

1 定位數學模型

將衛星1作為參考衛星，則雙星在時刻下觀測到的衛星2與1之間的TDOA定義為21,，即

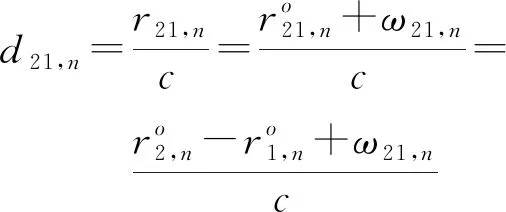
(1)

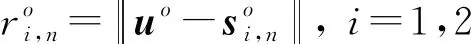
(2)

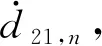
(3)

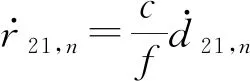
(4)

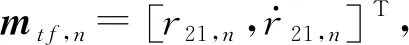
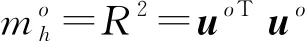
(5)

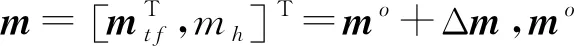
2 位置合批的融合算法

2.1 CRLB

由于考慮衛星存在誤差的情況，因此未知參數=[T,T]，令=[,]，則

ln(;)=ln(;)+ln(;)=

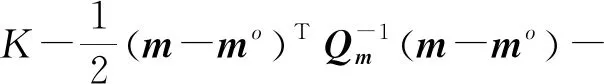
(6)

式中為常數。則未知參數的CRLB為

(7)

式中，

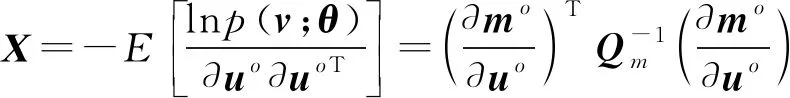
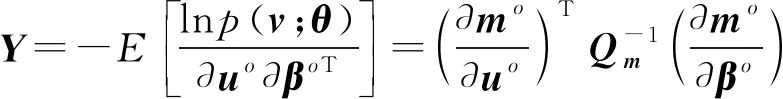
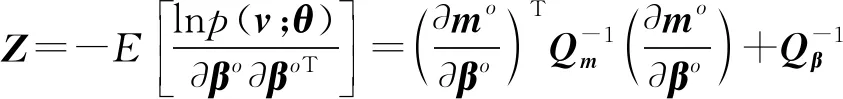
經計算可得輻射源的CRLB為

()=+

(-)

(8)

2.2 位置合批處理

工程上現有的位置合批處理方法主要有三種：一是取理論上的最優單次定位結果。假設在衛星過頂期間可以在個時刻截獲到輻射源信號，則將時刻的單次雙星時差頻差定位理論誤差設為(=1,2,…,)，理論上的最優單次定位結果表示為

(9)

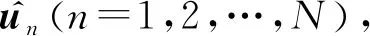
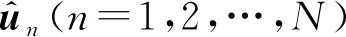
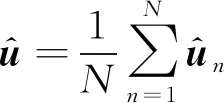
(10)

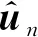
(11)

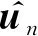
(12)

以上三種位置合批處理方法從理論上講并不是最優的數據融合方法：理論上的最優單次定位結果僅使用了一次觀測的數據；所有定位點的直接平均結果沒有考慮衛星編隊在不同位置下的定位精度是不同的；所有定位點的加權平均結果所使用的加權矩陣是單次定位所得。為此下文介紹了一種融合多次觀測數據的理論最優定位算法。

2.3 基于G-N迭代的時差頻差定位融合算法

本文算法參考文獻[10]給出了一種僅需估計的加權最小二乘算法，其表達式如下：

(13)

-1,,=1,…,,…,

(14)

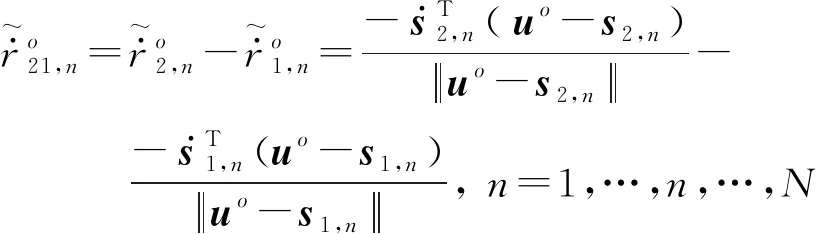
(15)

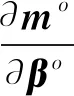
(16)

式中，為雅克比矩陣，

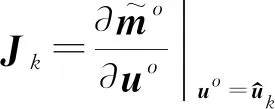
(17)

迭代初值可選取個觀測時刻中的任一時刻得到的單次定位結果，其單次定位求解可參考文獻[11]。通過球面迭代可將算法從正球面模型轉換到WGS-84橢球模型來提高定位準確性。

3 仿真分析

本節通過實驗驗證上述算法。令輻射源位置的經緯度分別為1178° W和196° N，其高程為零。用于實驗的衛星星歷點數據基于STK軟件生成，將同軌雙星的軌道高度設為1 100 km，軌道傾角設為634°，星間距設為104 km，軌道歷元時刻規定從2020年8月29日4時開始，衛星采樣間隔設為1 s，整軌取960個星歷點數據作為樣本。

將時刻下觀測的時差頻差誤差協方差陣,設為

(18)

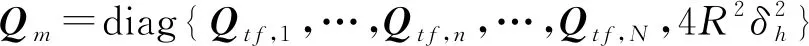
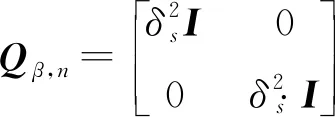
(19)

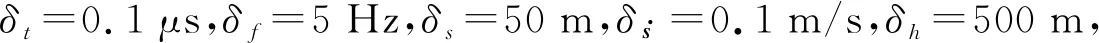
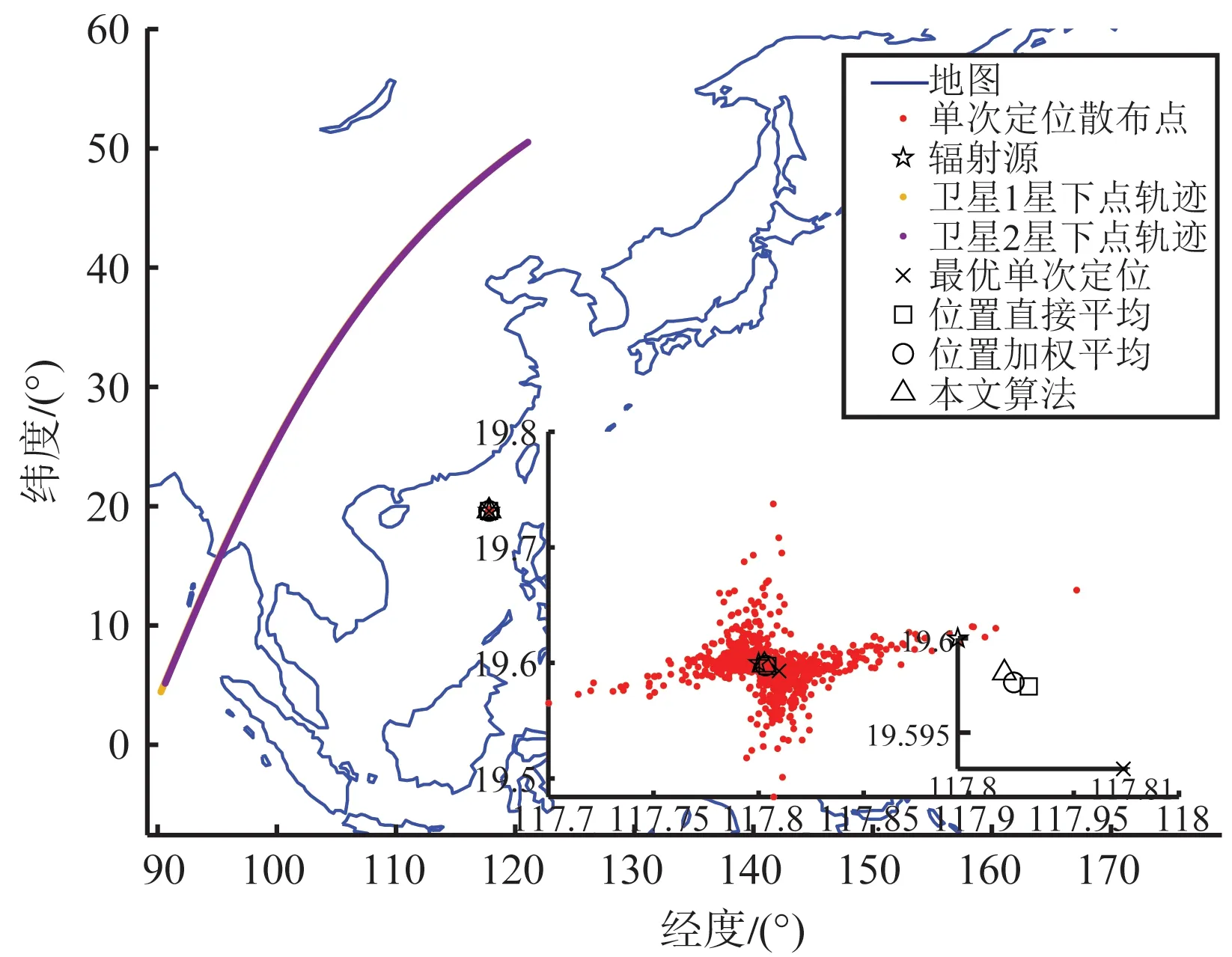
圖1 衛星星下點軌跡和各種方法的定位點分布

通過計算位置估計的均方根誤差(Root Mean Square Error，RMSE)來比較本文提出的算法和工程上常用的位置合批處理方法之間的性能，RMSE表達如下：

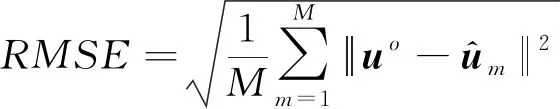
(20)

首先考慮理想情況下的電磁環境，這里的理想環境指衛星每秒都能截獲到輻射源信號，測量誤差和衛星誤差依然存在。我們取融合次數分別取30，60，120，240，320，480和960次，即對得到的960個星歷樣本每間隔960s進行一次均勻采樣，用采樣所得星歷點數據進行融合定位，比較不同融合次數下各種位置合批處理方法的定位精度，實驗結果如圖2所示。

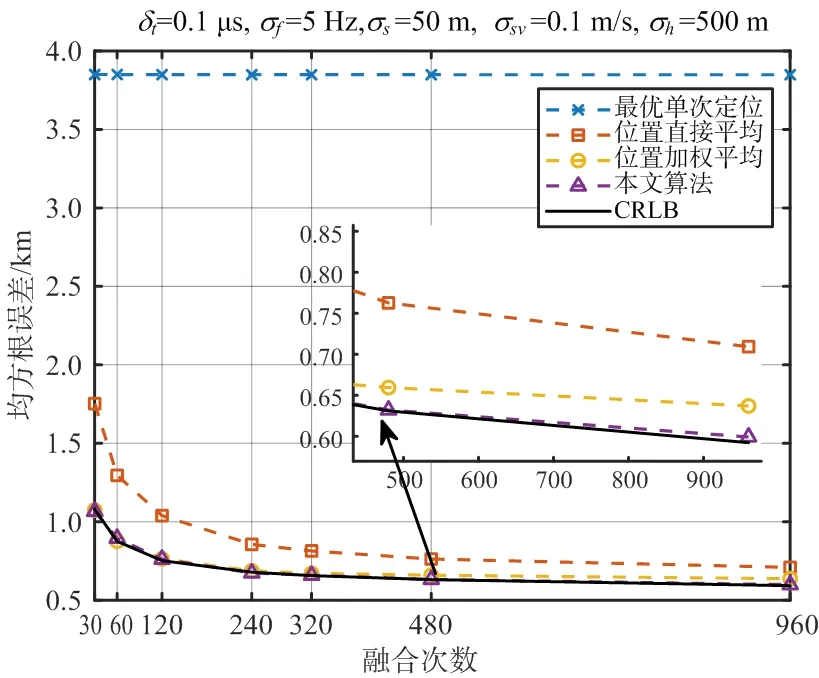
圖2 理想電磁環境各種方法的定位精度對比

通過實驗結果可以得出，在相同條件下，本文算法和位置加權平均都能達到CRLB，隨著融合次數逐漸增多，本文算法的性能開始優于位置加權平均，而位置加權平均性能開始偏離CRLB；位置直接平均的性能要次于前兩種方法，但是在融合次數較多的情況下要優于最優單次定位。

但是在實際工程應用中，空間電磁環境是復雜多變的，衛星過頂期間可能僅僅截獲幾次輻射源信號，因此這里取融合次數分別為2，3，4，5，6，8和10次，同樣對得到的960個星歷樣本每間隔960/s進行一次均勻采樣，用采樣所得星歷點數據進行融合定位，同樣比較不同融合次數下各種位置合批方法的定位精度，實驗結果如圖3所示。

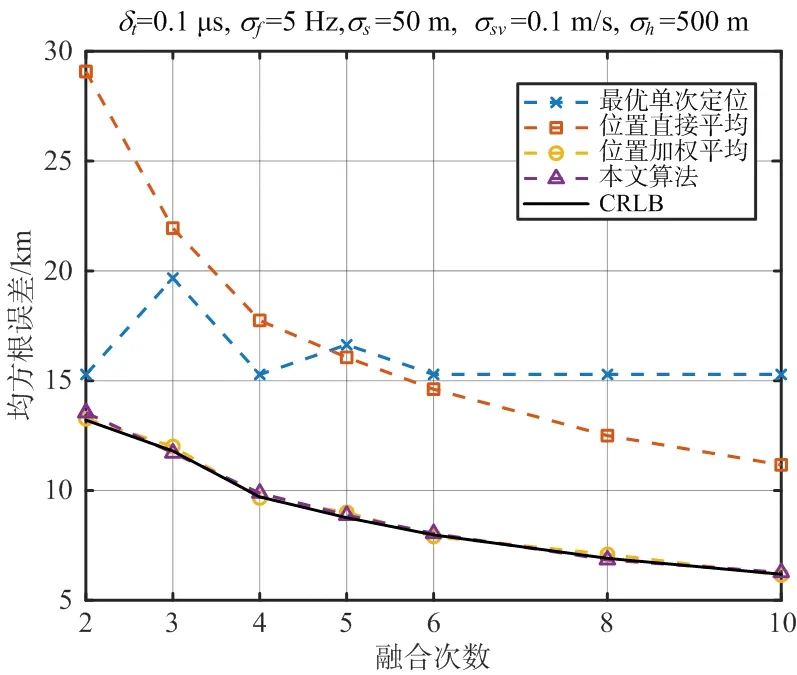
圖3 復雜電磁環境各種方法的定位精度對比

通過實驗結果可以得出，在相同條件下，本文算法和位置加權平均的性能都能達到CRLB且優于位置直接平均和最優單次定位；最優單次定位的性能一開始優于位置直接平均，當融合次數大于5次之后，位置直接平均的性能開始優于最優單次定位。

4 結束語

本文提出了一種基于G-N迭代的雙星時差頻差定位融合算法，有效地利用多次觀測的時差頻差和高程信息進行定位。通過實驗驗證，本文算法在理想電磁環境和復雜電磁環境下的定位精度要優于工程上現有的最優單次定位、位置直接平均和位置加權平均等位置合批處理方法。