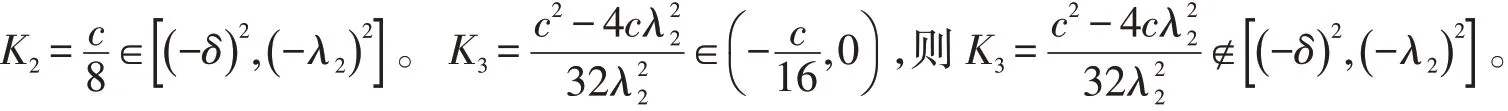復射影空間CP n(c)中A2型實超曲面上Sasaki磁場下的外在圓軌道

劉曉周，包圖雅

（內蒙古民族大學 數理學院，內蒙古 通遼 028043）

研究子流形的方法有很多種，其中一種方法是通過研究子流形上的曲線，進而得出子流形的特征。對于子流形上曲線的研究，可以將其放到其外圍空間去考慮。對于曲面上的曲線，一般取測地線、圓等特殊曲線進行研究，同時通過對特殊曲線上指標的分析，能夠豐富曲面理論。

根據正則截面曲率c的值，非平坦復空間CMn(c)被分為復射影空間CPn(c)（正則截面曲率c>0）和復雙曲空間CHn(c)（正則截面曲率c<0）［1］。復射影空間中霍普夫齊性超曲面被TAKAGI［2］和KIMURA等［3］分為A型、B型、C型、D型和E型，其中A型被分為A1型和A2型［2-3］。文獻［4］研究了非平坦復空間中A型實超曲面（即測地球）上的圓軌道，給出了A型實超曲面的特征。文獻［5］通過研究K?hler流形中實超曲面上Sasaki磁場下二階相切軌道，給出了K?hler流形中的實超曲面的特征。文獻［6］研究了復射影空間中A1型實超曲面上Sasaki磁場下的外在圓軌道，給出了A1型實超曲面的特征。文獻［7］計算了復射影空間中B型實超曲面上Sasaki磁場下軌道的外在形狀為二階相切時，對應的外在測地曲率和外在復撓率的值。沿著這個思路，筆者根據復射影空間中A2型實超曲面上Sasaki磁場下軌道的外在形狀成為圓的條件，分析了復射影空間中A2型實超曲面上Sasaki磁場下外在圓軌道的外在測地曲率和外在復撓率之間的關系。

1 基礎知識

非平坦復空間CMn(c)中的實超曲面M上有近切觸度量結構，該近切觸度量結構由張量、向量場ξ=-JN、1-形式和非平坦復空間上的度量所決定，其中，N是非平坦復空間中實超曲面M上的單位法向量，v是任意點處的切向量［1］。復射影空間CPn(c)中A2型實超曲面M是繞全測地CPl的管Tl(r)(1 ≤l≤n-2)，其中,。復射影空間CPn(c)中A2型實超曲面M有3個主曲率，分別是對應與ξ垂直方向的主曲率和，以及對應ξ方向的主曲率［2-3］。在非平坦復空間CMn(c)中的實超曲面M上，2-形式的常數倍Fk=kF?(k∈R)被稱為是Sasaki磁場，滿足的弧長參數化的光滑曲線γ被稱為Sasaki 磁場Fk下的軌道。對非平坦復空間中實超曲面M上Sasaki磁場下的軌道稱為構造撓率，構造撓率 |ργ|≤1。?是非平坦復空間中實超曲面M的外圍流形，l:M→?是一等距浸入映射。當等距浸入映射l把M上的光滑曲線γ映射到M的外圍空間?上時，稱曲線l°γ為γ的外在形狀。高斯公式和魏因加爾吞公式分別為和

定義1［1］非平坦復空間CMn(c)中實超曲面M上弧長參數化的光滑曲線γ如果滿足，則稱曲線γ的外在形狀是圓。

定義2［1］非平坦復空間CMn(c)中弧長參數化的光滑曲線γ的測地曲率kγ被定義為的復撓率τγ被定義為

2 主要結果

文獻［5］給出了非平坦復空間CMn(c)中A型實超曲面M上Sasaki磁場Fk下的軌道的外在形狀為圓的條件，下面根據復射影空間CPn(c)中A2型實超曲面M的情況，計算復射影空間CPn(c)中A2型實超曲面M上Sasaki磁場Fk下軌道的外在形狀成為圓的條件。

命題1復射影空間CPn(c)中A2型實超曲面M上Sasaki磁場Fk下的軌道γ滿足下面條件之一時，其外在形狀成為圓。

證明對于復射影空間CPn(c)中A2型實超曲面M上Sasaki磁場Fk下的軌道γ，有是任意點處的弧長參數化曲線的切向量，?可以寫成

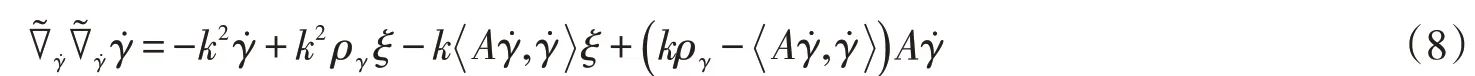
根據（9）式，如果軌道γ的外在形狀為圓，則有

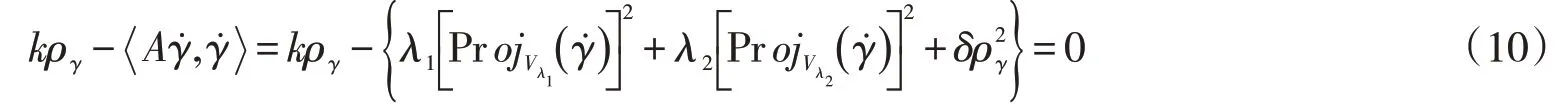
下面分析（11）式。

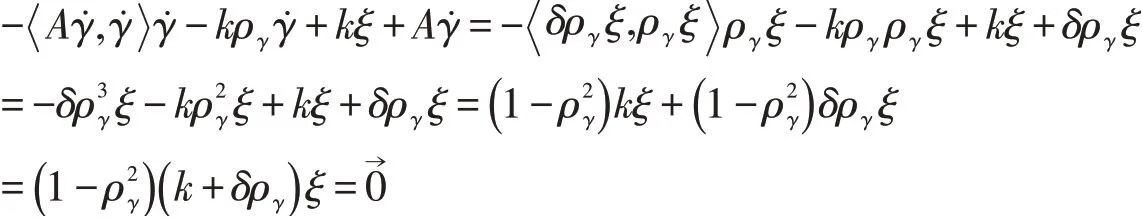
即ργ=±1或k=-δργ。

ργ=±1是軌道γ外在形狀成為圓的第一個條件。而且k=-δργ是軌道γ外在形狀成為圓的第二個條件的特例。

要使上式成立，則每一個分量都需要為0，即

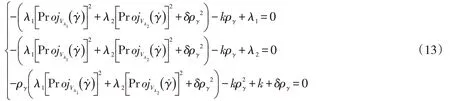
文獻［5］給出了非平坦復空間中A型實超曲面上Sasaki磁場下外在圓軌道對應的外在測地曲率kγ和外在復撓率τγ，下面具體給出復射影空間CPn(c)中A2型實超曲面的情況。

命題2復射影空間CPn(c)中A2型實超曲面M上Sasaki磁場Fk下外在圓軌道γ對應的外在測地曲率kγ和外在復撓率τγ如下：

命題2中（1）和（2）的外在復撓率的絕對值為1，不隨著外在測地曲率的變化而變化。下面分析命題2中（3）的外在測地曲率和外在復撓率之間的關系。

定理1當且k-λ1ργ+δργ=0時，復射影空間CPn(c)中A2型實超曲面M上Sasaki磁場Fk下外在圓軌道γ的外在測地曲率為，外在復撓率的平方

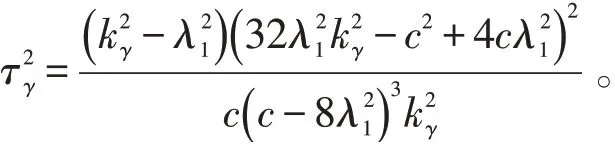
定理2當且k-λ1ργ+δργ=0時，復射影空間CPn(c)中A2型實超曲面M上Sasaki磁場Fk下外在圓軌道γ的外在測地曲率的取值范圍為：

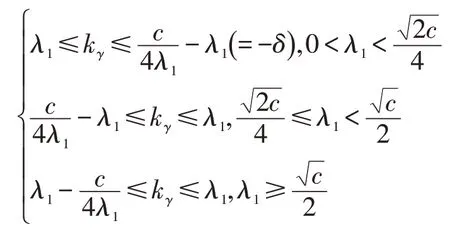
定理3當且k-λ1ργ+δργ=0時，復射影空間CPn(c)中A2型實超曲面M上Sasaki磁場Fk下外在圓軌道γ上g(K)關于K的單調性如下：

定理4當且k-λ2ργ+δργ=0時，復射影空間CPn(c)中A2型實超曲面M上Sasaki磁場Fk下外在圓軌道γ的外在測地曲率為

證明復射影空間CPn(c)中A2型實超曲面的主曲率，則有

將（4）式和（6）式代入到測地曲率的定義中有

證畢。

對于復射影空間CPn(c)中A2型實超曲面，有，主曲率λ2<0。下面討論時，復射影空間CPn(c)中A2型實超曲面M上Sasaki磁場Fk下外在圓軌道的外在測地曲率的取值范圍。

定理5當且k-λ2ργ+δργ=0時，復射影空間CPn(c)中A2型實超曲面M上Sasaki磁場Fk下外在圓軌道γ的外在測地曲率的取值范圍為：

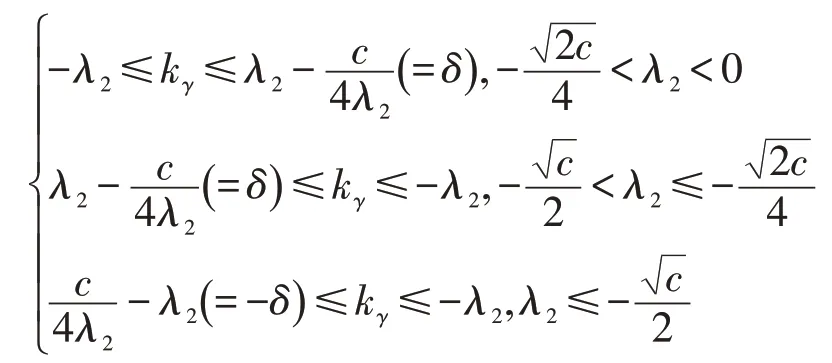
證明當ργ=0時，kγ=-λ2。

定理6當且k-λ2ργ+δργ=0時，復射影空間CPn(c)中A2型實超曲面M上Sasaki磁場Fk下外在圓軌道γ的復撓率的平方

證明將（4）式和（5）式代入到復撓率的定義中有

證畢。

定理7當且k-λ2ργ+δργ=0時，復射影空間CPn(c)中A2型實超曲面M上Sasaki磁場Fk下外在圓軌道γ上g(K)關于K的單調性如下：

證明對

下面計算g(K)在穩定點處以及端點處的函數值，根據（21）式，有

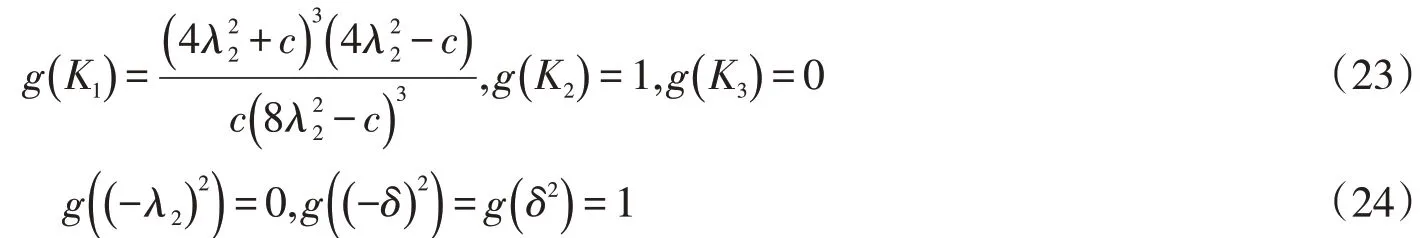
根據（21）式，g(K)在上是連續的。

根據（21）式，g(K)在[δ2,( -λ2)2]上是連續的。

根據（23）式，有0

根據（21）式，g(K)在[(-δ)2,(-λ2)2]上是連續的。

根據（21）式，g(K)在[(-δ)2,(-λ2)2]上是連續的。