關于氦原子基態能量一級微擾的研究
2022-03-31 02:35:04劉榮
廣西物理 2022年3期
劉榮
(廣西醫科大學玉林校區,廣西 玉林 537406)
0 引言
量子力學是研究描述微觀粒子結構及其運動規律的學科。物質的電子分布可由它的狀態來描述,此狀態函數由薛定諤方程決定。對于具有兩個以上電子的原子,如氦原子,其狀態函數必須同時描述這些的運動規律,要從其對應的薛定諤方程式直接解出,幾乎是不可能的事。為此用來處理多電子原子的方法,其中之一就是微擾理論法。多電子體系在一級微擾計算下往往跟實驗值相比誤差不算特別大,對于求解相應的體系的能量或其他相關參數會取得相對可以接受的結果。
1 微擾理論和計算方法
1.1 非簡并定態微擾理論
比較方程兩邊λ的同次冪項,可得各級近似的方程:
1.2 氦原子基態能量計算
氦原子核外有兩個電子。氦原子的哈密頓算符是:
不難看出,電子的能量以及波函數符合:
由以上各式得,C1,C2滿足的方程是:
式中決定微擾能量一級修正的久期方程是:
這是單態而非簡并。用非簡并微擾直接計算能量的一級修正。結果是:
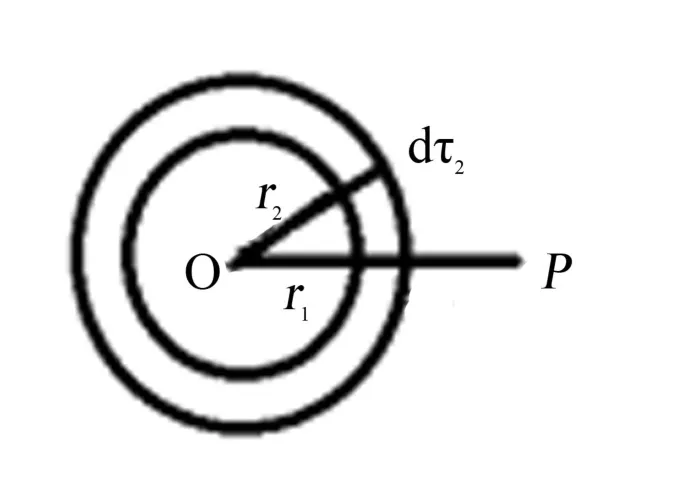
圖1 輔助求解的靜電勢球
代入(14)式中,得到基態能量的一級修正:
于是可以求得一級微擾下的基態能量為:
2 結果和結論
通過上面的一系列的理論推導,我們已經求的一級微擾下的氦原子基態能量為 -74.83eV,而相關研究證實,二級微擾下的氦原子基態能量為-76.1eV,而氦原子基態能量的實際測量值為-78.98eV,為此,通過一級微擾理論所得的計算值的相對誤差為:×100%=5.3%。通過本文對氦原子基態能量的一級微擾計算,我們可以推廣對于其他多原子基態能量以及激發態能量的計算我們只要計算到一級微擾還是接近實際數值了,二級、三級微擾誤差不是很大了,而且三級以上微擾的計算非常復雜,對此我們采取一級微擾基本可以達到解決問題。

