橋梁轉體T構不平衡力矩測試技術研究
鐘丹丹
(中鐵二十五局集團第四工程有限公司,廣西 柳州 545007)
0 引言
由于轉體球鉸體系在制作、安裝、T構兩端砼澆筑及梁體預應力施加存在操作誤差等原因,轉體T構兩懸臂梁段重量作用于球鉸中心的力矩不同,即存在不平衡力矩,過大的不平衡力矩會使T構沿連續梁縱軸線的豎平面轉動,導致安全事故發生。為確保轉體施工能夠順利、安全進行,需要對T構進行不平衡力矩測試(簡稱“稱重”),以確定T構重心偏移量、制定配重方案、調整重心至合理區間內。本文依托南寧市亭洪路延長線(規劃七路~南建路)工程上跨鐵路立交橋主跨2-80.0 mT形鋼構橋轉體施工實踐,詳細闡述轉體T構稱重、配重的試驗方法。
1 工程概況
南寧市亭洪路延長線(規劃七路~南建路)工程上跨鐵路立交橋工程,位于南寧市江南區鐵路南化站附近,橋上設置雙向六車道,按兩幅設計。上部結構為單箱三室斜腹板箱形截面,2-80.0 mT形鋼構橋按兩幅橋進行布置,跨越既有南化站。
上部結構主橋T構采取滿堂支架現澆后,再平面轉體施工。為確保轉體施工的安全進行,在轉體前對T構進行稱重,并據此配重、調整T構重心。
2 稱重方法及原理
2.1 測試不平衡力矩的方法
本次不平衡力矩的測試(簡稱稱重)方法為球鉸轉動法,該法通過向轉體T構施加頂力,測試當T構位移突變(臨界狀態)時所施加的頂力,通過其此時的力矩平衡條件計算T構的不平衡力矩及重心偏移值[1],作為轉體施工決策和配重方案的依據。該法因操作簡便、結果準確、費用低的優勢而得到廣泛使用。
測試前,拆除澆筑0號塊的鋼管支架,解除T構與承臺間的固結措施,此時,上轉盤及T構組成整體的剛體,然后對T構施加轉動力矩,使轉動力矩均勻、緩慢地增加,直到球鉸結構兩轉盤間出現轉動位移,即位移發生突變。此時,施加的外力矩使T構能夠克服球鉸靜摩阻力矩而出現微小的相對轉動,且處于靜、動的臨界狀態。在此狀態下,球鉸間摩阻力矩(MZ)、T構的不平衡力矩(MG)及施加的外部力矩構成一種平衡狀態。由此平衡條件可將摩阻力矩(MZ)、不平衡力矩(MG)計算出來。
2.2 計算球鉸間摩阻力矩(MZ)和轉體T構不平衡力矩(MG)
T構完成支架的脫離后,通常T構體系處于如下2種平衡形式之一:①形式1。如果沒有撐腳支撐在滑道的鋼板上,說明球鉸間摩阻力矩(MZ)較轉體T構不平衡力矩(MG)要大,故T構沒有發生上、下轉盤之間的轉動。T構平衡狀態是由轉體T構不平衡力矩和球鉸間摩阻力矩所構筑;②形式2。如果有撐腳支撐在滑道的鋼板上,則表明不平衡力矩(MG)大于摩阻力矩(MZ),故T構球鉸發生轉動,直至撐腳支撐在滑道上,此時,轉體T構的平衡狀態是由轉體T構不平衡力矩、球鉸間摩阻力矩和撐腳反力力矩所構筑。
2.2.1 形式1平衡狀態下的測設及數據計算方法
形式1平衡狀態的稱重方法為:分別從T構的東、西(如圖1、圖2所示)側設置支點施加頂力,使轉體T構沿縱軸的豎平面內出現順、逆時針的微小轉動。記錄測試過程中位移傳感器和壓力傳感器的讀數。頂力逐級增加,當位移傳感器的讀數出現突變時,表示T構已產生轉動、處于臨界狀態。

圖1 在西側施加頂力時T構力矩平衡關系

圖2 在東側施加頂力時T構力矩平衡關系
假定圖1、圖2中的不平衡為向東側偏移,而球鉸間摩阻力矩(MZ)總是相反于轉動方向。根據轉體T構在豎平面內的力矩平衡關系,計算過程如下:
由(1)、(2) 式計算出:
式中,P1、P2在T構產生微小轉動時,在其西、東側施加的外力值(kN);L1、L2為頂力的合力對球鉸中心的力臂(m)。
2.2.2 形式2平衡狀態下的測設及數據計算方法
此狀態下,T構因自身不平衡力矩大于摩阻力矩而轉動,假定不平衡力矩(MG)向東偏移,即東側的撐腳與滑道接觸。此時稱重方法為:先在T構東側設置千斤頂支點進行施力,使轉體T構沿梁縱軸的豎平面內出現順時針微小轉動,然后落頂,使T構發生微小逆時針轉動。記錄測試過程中頂升、落頂過程中突變時位移傳感器和壓力傳感器的讀數。根據圖3、圖4中轉體T構在豎平面內的力矩平衡關系,計算過程如下:

圖3 東側頂升T構力矩平衡關系
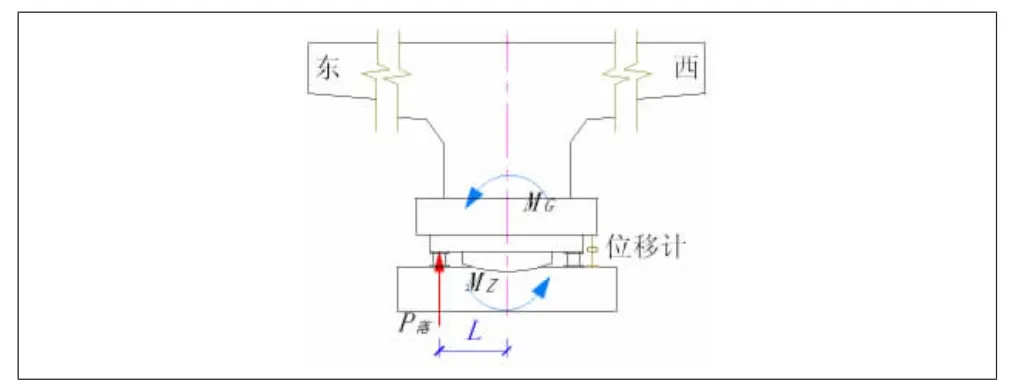
圖4 東側落頂T構力矩平衡關系圖
由(5)、(6) 式計算出:
式中,P升、P落為T構產生微小轉動時,在東側施加(升、落)的外力值(kN);L為施力合力對球鉸中心的力臂(m)。
2.3 球鉸靜摩擦系數及T構偏心距計算
本項目采用四氟乙烯制作鉸片,在上下轉盤間填充黃油,根據相關文獻的研究成果,采用下式計算球鉸靜摩阻系數、偏心距[2]。
式中,N為轉體T構的總重量;R為球鉸弧形的圓半徑。
3 稱重的實施
3.1 估算千斤頂與壓力傳感器的噸位
T構重量荷載F總=140 000 kN。按以往的工程實際,靜摩擦系數μ的取值范圍為0.05~0.07[3]。球鉸的半徑R為7.992 m,角度為28.985度,摩擦系數取大值(0.07),按公式(8)可計算得靜摩擦力矩為
本次稱重在上轉盤承臺下施加頂力,頂力距球鉸中心線約為5.0 m,稱重時在轉盤兩側共設置6臺千斤頂對(即每側3臺)T構施加頂力。則每臺千斤頂需要的頂力計算得:35 882.41/(3×5.0)=2 392.16 kN。
考慮到加載時的對稱性及施力時的安全性,每側配備5000 kN千斤頂3臺,相應配置5000kN壓力傳感器。
3.2 測試儀器和設備
(1)位移傳感器。本項目設置6個傳感器量測T構的微小位移,采用應變式位移傳感器,該類型傳感器不易受其它因素干擾,適用性強,其測量精度為1/1 000,量程為±5mm,線性度大于0.2%。
(2)壓力傳感器。設置6個壓力感器以測量T構對千斤頂的反力,壓力傳感器型號為BLR-3型,其測量精度為±1%。,量程為5000kN,靈敏系數為2.0。
(3)數據采集系統。為滿足稱重測試的要求,采用IOTECHWaveBook512數據采集系統,其采樣率為100萬次/s;分辨率為12bit;有40個電壓通道,16個動態應變通道。
(4)數據分析軟件系統。數據分析軟件系統引進美國的DADiSP數據分析軟件包,該軟件包能夠對測試所得數據進行自動、直觀的處理及分析。
(5)I20a工字鋼基座。基座帶加勁肋,長度約為60 cm,根據支撐點數量、千斤頂高度及支點處上下承臺間的間距確定工字鋼基座數量、設置厚2 cm的50 cm×50 cm鋼板(每個支點2塊)共6塊。
3.3 解除臨時固結措施,拆除砂箱及撐腳下的沙盤
在解除臨時固結措施和拆除砂箱及撐腳下的沙盤之前,在上承臺四周埋設千分表記錄初始讀數。拆除過程中注意每拆除一組支撐,觀察千分表并記錄讀數,并觀察隨著砂箱的拆除,撐腳是否向一側連續下沉。完全拆除后測定撐腳與滑道之間間隙變化和梁體豎向位移,并據此判斷轉體體系處于何種平衡方式,進而確定稱重方案。
3.4 判定轉動體系的平衡狀態
當所有支撐完全拆除后,根據測定撐腳與滑道之間間隙變化和梁體豎向位移,判斷轉體體系的平衡狀態。
(1)如果全部撐腳處于懸空狀態,表明MZ(球鉸摩阻力矩)>MG(T構不平衡力矩),采用縱向兩側分別測試不平衡力矩的方案。
(2)如果撐腳與滑道鋼板產生接觸,相對應的另一側撐腳與滑道鋼板相距縫隙變大,表明MZ(球鉸摩阻力矩)<MG(T構不平衡力矩)。假定不平衡力矩MG向東偏,先在T構東側頂升梁體,當T構沿縱向軸線的豎平面發生微小轉動后再落頂,直至T構發生微小轉動。
3.5 試驗實施
本項目先進行左幅橋T構的稱重,全部拆除砂箱、固結措施后,觀察到左幅橋T構處于第1種平衡型,故按下程序進行稱重試驗:
(1)將千斤頂置于撐腳與滑道間隙較小的那一側,安裝鋼墩、鋼板及傳感器等。
(2)調整千斤頂,施加初始頂壓力至全部千斤頂,對加載體系進行預頂、記錄此時油表讀數。
(3)千斤頂回油卸落后與轉動體稍微脫離,使壓力傳感器、千分表凋零。
(4) 千斤頂逐級加力,級差大約控制為300~500 kN,記錄各級的力值,并記錄相應的位移,持續加載至位移突變。繪制“力—位移(P△)”曲線,找出臨界狀態的拐點。
(5)每側加載平行測試兩次,并對結果進行比較(若兩次結果偏差過大,重新測試)。
(6)從另側頂升,重復實施上述測試。
3.6 測試儀器的布置
在左幅橋T構的東、西兩端,距球鉸中心5.0 m處分別布置3臺千斤頂,在千斤頂上安裝壓力傳感器(布置方法如圖5所示)。

圖5 稱重試驗設備及測點布置圖
4 試驗數據處理及配重方案
根據上述稱重試驗的數據,繪制并分析“力—位移(P△)”曲線圖(如圖6所示),找出臨界狀態的拐點,確定臨界狀態時的頂升力(P)。

圖6 左幅橋T構稱重的P△曲線圖
(1) 左幅橋T構
因左幅橋T構是第1種平衡形式,稱重完畢后,繪制并分析“力—位移(P△)”曲線(如圖6所示)。由公式(3)和公式(4)可計算出不平衡力矩(MG)和摩阻力矩(MZ)。
進而根據公式(10)算出靜摩擦系數(u),根據公式(11) 算出偏心距(e)。
測試數據的分析計算結果見表1。

表1 左幅橋T構稱重測試分析計算表
分析表1所列的計算數據,左幅橋T構的兩端存較不平衡力矩,偏心距e=0.33 m,位于東側。由于偏心距過大(設計要求偏心距≤5 cm)。該轉體T構采取在西側距球絞中心65 m處設置配重的方案,完成配重后,再進行稱重,得調整后的偏心距e=2.1cm,達到轉體要求。
(2) 右幅橋T構
右幅橋T構也是第一種平衡狀態,測試數據的分析計算結果見表2。

表2 右幅橋1號墩T構稱重測試分析計算表
分析表2所列的計算數據,右幅橋T構的兩端雖存在一定的平衡力矩,偏心距e=0.029 m,位于東側。由于偏心距≤5 cm,故轉體T構的重心偏移在誤差允許范圍內,不需重新調整。
5 結語
本項目的T構球鉸轉動法稱重采用壓力傳感器、位移傳感收集與傳輸試驗數據,運用先進處理軟件對數據進行分析、處理及直觀顯示,使試驗更科學、測試結果更精準、數據處理更快捷。達到準確測試轉體系統的不平衡力矩的目的,為調整重心配重提供決策依據,確保轉體施工安全、順利。同時,還能夠通過測試所得數據計算出摩阻系數、摩阻力矩,作為轉體施工時牽引力的計算依據,保證牽引系統轉體時的安全可靠性。

